变加速运动目标的相参积累算法*

2020-05-18辛婷婷王国宏张亮张翔宇

现代防御技术 2020年2期

辛婷婷，王国宏，张亮，张翔宇

(海军航空大学信息融合研究所，山东烟台 264001)

0 引言

近几十年来，随着人们对飞行器越来越深入地研究，飞行器得到了很大的发展，越来越多的新型飞行器进入了人们的视野，它们普遍具有高速度、强机动性和低雷达散射截面积等特点，这使得传统雷达探测目标的方法受到了极大地挑战。传统的雷达检测目标方法一般采用长时间相参积累的方法，然而对于新型飞行器，它们具有的特点使得目标回波在很短的时间内跨越多个距离单元和多普勒单元，即发生距离走动和多普勒走动现象。也就是说，采用传统的检测方法会使回波能量分散在多个单元，无法实现能量的有效积累，这就给这类目标的检测带来了极大地挑战，针对这类目标的检测问题亟需解决。

针对具有变加速运动模型的高速机动目标的检测问题，目前已经提出了很多相参积累算法。在文献[1-3]的基础上，文献[4]提出的基于慢时间序列翻转变换-二阶keystone变换-吕分布(time reversing-second crder keystone transrorm-LV′s distribution,TRT-SKT-LVD)的算法中，吕分布依赖于雷达提供至少 1 s的冗余信息，并且受限于线性调频信号的中心频率和调频斜率的估计范围[5]，所以TRT-SKT-LVD算法受限于波长长度、速度取值和加速度取值，不适用于波长较短、机动性强的场景[6]。文献[7]提出的长时间相参积累的算法能够弥补二阶keystone变换插值带来的损失，使积累效果更好，但是该方法涉及对加速度的搜索、搜索参数容易产生误差，尤其是在低信噪比下，误差容易越来越大。文献[8]提出的基于广义keystone变换和广义去调频(generalized keystone transform generalized dechirp,GKT-GDP)算法中，涉及多次keystone变换和对多普勒模糊数、加速度和加加速度的搜索，运算极其复杂，计算量很大。

为了能够很好地检测目标，同时减少计算量，又能适用于速度较高、机动性较强的场景，本文提出了基于慢时间序列翻转变换-二阶keystone变换-双正交傅里叶变换(TRT-SKT-BFT)的相参积累算法。首先，对频域脉压信号进行慢时间序列翻转变换得到翻转后的频域信号形式，再将其与频域脉压信号相乘，同时校正由速度和加加速度引起的距离走动和加加速度引起的多普勒走动。其次，采用二阶keystone变换的方法，校正由加速度引起的距离弯曲。最后，将距离走动校正后的信号看做关于慢时间变量的线性调频信号，采用双正交傅里叶变换估计调频斜率的方法[9]，估计出相应的加速度值，并实现相参积累。本文所提算法无需进行参数搜索[10-11]，极大地减少了运算量，且只涉及一次非线性变换，二阶keystone变换和双正交傅里叶变换均为线性变换，有效地地减少了信噪比的损失，在多目标检测中减少了交叉项的影响。

1 回波模型[12]及分析

假设雷达探测区域内存在一变加速运动目标，该目标与雷达的初始径向距离为R0，初始径向速度为a1，初始径向加速度为a2，初始径向加加速度为a3。若雷达在一个扫描周期内发射一串脉冲，脉冲个数为M，脉冲重复周期为Tr，则在积累时间T=MTr内，目标与雷达之间的径向距离为

(1)

则雷达收到目标回波的时延为

(2)

式中：tm=mTr(m= 0,1,2,…,M-1)为慢时间；c为光速。

假设雷达发射的脉冲为线性调频信号(linear frequency modulated,LFM)，则雷达接收到的回波信号为

(3)

经过去载频得到基带回波信号为

exp(-j2πfcτm).

(4)

对基带回波信号进行脉冲压缩，得到时域脉压信号

(5)

式中：A1为脉压后时域信号幅度，Sinc()为辛格函数。脉压后信号的包络位置随着慢时间变化发生变化，速度、加速度、加加速度都会影响包络的位置，当变化量比较大，超过距离分辨单元时，就会发生距离走动现象。

对于指数相位项，多普勒频率不再是一个固定值，瞬时多普勒频率可以表示为

(6)

多普勒频率随着慢时间变化而变化，主要受加速度和加加速度影响，当多普勒频率的变化量超过多普勒分辨单元时，就会发生多普勒走动现象。

将式(5)沿着快时间维进行快速傅里叶变换(fast fourier transform,FFT)变换，得到脉压信号在频域的表现形式

(7)

式中：A2为频域脉压信号的幅度。

2 算法原理

变加速运动具有多种距离走动和多种多普勒走动，依次校正较为复杂。本文提出用BFT(Biothogonal Fourier Transtorm)来实现积累，在算法实现上减少了复杂度，且具有良好的性能。本小节将介绍所提算法的原理[13]。

2.1 慢时间反转变换

考虑到要沿着慢时间维对序列进行反转，慢时间可以写成对称形式为

(8)

此时可以将距离频域脉压信号改写为

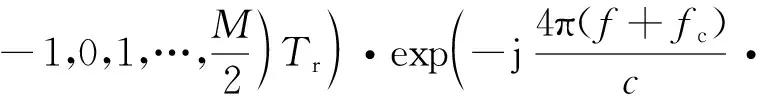
(9)

则式(9)的慢时间序列反转结果为

(10)

将式(9),(10)相乘得

(11)

从式(11)可以看出，与速度和加加速度有关的相位项相互抵消，相应地由速度引起的线性距离走动、由加加速度引起的三阶距离走动和多普勒弯曲已经被同时消除，但是，由加速度带来的距离弯曲和线性多普勒走动依然存在。

2.2 二阶keystone变换

对于加速度引起的距离弯曲，一般采用二阶keystone变换来进行校正[14-15]，其变换关系式为

(12)

将式(12)代入式(11)中，得到

(13)

此时加速度与距离频率的耦合已经消除，将其沿着快时间维作逆傅里叶变换，得到

(14)

式中：A3为二阶keystone变换后时域信号的幅度。

从式(14)可以看到，二阶keystone变换后，时域回波信号的包络中心都位于同一距离单元内，包络位置只与初始径向距离有关，即距离走动已经得到校正，能够影响能量积累的只剩下加速度引起的多普勒走动。

2.3 双正交傅里叶变换

距离走动后的时域信号形式可以写为如下形式：

(15)

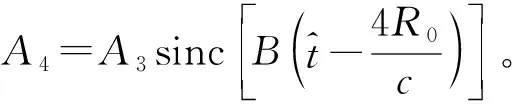
式(15)可以看成关于慢时间变量的信号，恰好满足线性调频信号x(t)=Aexp(j(φ+Kπt2))的形式，其中φ为初始相位，K为调频斜率。故可以将式(15)写成相应的形式，即

(16)

双正交傅里叶变换的公式为

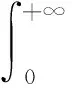
(17)

对式(15)进行双正交傅里叶变换，得到

(18)

(19)

3 算法流程及运算复杂度分析

3.1 算法实现

根据第2节所提算法原理，本文所提算法的具体实现步骤如下：

步骤1：确定径向距离的范围[r1,r2]、距离分辨间隔ΔR=c/2B，相应的距离单元数量为Nr=round((r1-r2)/ΔR)；

步骤2：对接收的雷达回波信号进行去载频、脉冲压缩并将其变换到距离频域得到Src(f,tm)；

3.2 运算复杂度分析

假设Nr=M=Nτ=NF=Na2=Na3，则上述算法运算复杂度分别为O(6M3lbM+M3),O(M3lbM+M3),O(M2lbM+3M3+0.5M4lbM)和O(3M2lbM+M3)，所以本文所提算法在运算复杂度上具有优越性。

4 仿真分析

雷达系统参数设置如表1所示。

表1 雷达系统参数Table 1 Radar system parameters

4.1 算法性能证明

假设有一高速机动运动目标，它与雷达之间的初始径向距离为R0=151 km，初始径向速度为a1=300 m/s，初始径向加速度为a2=100 m/s2，初始径向加加速度为a3=90 m/s3。在信噪比为-5 dB的条件下，仿真结果如图1所示。图1a)为脉压结果，目标发生了很严重的距离走动现象，目标回波跨越了50个距离单元，这主要是由于目标具有较高的速度和较强的机动性造成的。图1b)为MTD积累结果，从三维的角度能看到能量发生了扩展，分布在多个多普勒单元和距离单元，利用此时的结果是无法获得目标运动信息的。图1c)为TRT结果，此时能量在距离-多普勒维的分布成对称弯曲状态，说明此时只有加速度带来的距离弯曲，由速度引起的线性距离走动和加加速度引起的三阶距离走动已经得到校正。图1d)为SKT结果，此时能量都集中到同一个距离单元内，说明距离弯曲得到有效校正。图1e)为相参积累结果，经过双正交傅里叶变换后，能够积累出一个很高的峰值，且峰值较为陡峭，没有较宽展宽。由图1的仿真结果表明，本文所提算法能够较好地实现变加速运动目标距离走动的校正和目标回波的相参积累。

4.2 几种算法比较

设脉压前信噪比为-20 dB，目标运动参数同4.1，仿真了在低信噪比条件下，基于速度补偿TRT-SKT-BFT算法的积累性能，并与MTD,KT-GDP、TRT-SKT-LVD和TRT-相位补偿等算法进行了比较，仿真结果如图2所示。图2a)为脉压结果，目标回波还没有完全淹没在噪声中，发生了很严重的距离走动。图2b)为MTD积累结果，此时回波能量虽然没有完全淹没在噪声中，但是能量展宽无法检测到目标。图2c)为KT-GDP积累结果，此时能积累出较高峰值，因为该算法中不涉及非线性运算，不会发生信噪比损失，但是积累有些扩展，这主要是低信噪比下搜索产生误差带来的影响。图2d)为TRT-SKT-LVD积累结果，此时无法实现积累出峰值，说明该方法受参数影响较大，脉冲积累个数、距离采样间隔以及载频等都对积累结果产生极大地影响。图2e)为文献[7]中所提TRT-相位补偿积累结果，此时该算法不具有很好的积累效果，受参数搜索误差影响。图2f)为本文所提的TRT-SKT-BFT算法，该算法在较低信噪比下依然能够实现积累，积累效果明显好于其他方法。由图2的仿真结果可以看到，本文所提方法在较低的信噪比下，依然能够积累出较高的峰值，并且相比于其他几种方法，抗噪声性能更强。

图1 单目标TRT-SKT-BFT算法的积累性能Fig.1 Accumulation performance of single-target based on TRT-SKT-BFT algorithm

4.3 多目标检测

假设有4个运动目标，分别为目标A、目标B、目标C和目标D，其运动参数如表2所示。

设脉压前信噪比为-6 dB，仿真结果如图3所示。图3a)～d)为目标A和目标B的积累过程，可以验证该算法不受速度和加加速度影响，只要加速度相同，则积累结果都位于同一调频斜率单元，可以根据所在距离单元来分辨目标所处位置。图3a)为脉冲压缩结果，2个目标都发生了明显的距离走动。图3b)为TRT结果，由于TRT为非线性运算，此时产生了交叉项且具有明显的距离走动，另外2项为自聚焦项，与单目标结果相同。图3c)为SKT结果，此时自聚焦项的弯曲得到了校正，但是交叉项依然存在走动。图3d)为积累结果，目标A和目标B都能得到积累，且位于同一调频斜率单元，这是因为2个目标具有相同的加速度，而交叉项得到了有效抑制，不影响目标积累。

图3e)～h)为目标A和目标C的积累过程，可以验证该算法速度和加加速度不变而加速度变化的结果，为了方便观察，设两目标的初始径向距离不同。图3e)为脉冲压缩结果，2个目标都发生了明显的距离走动。图3f)为TRT结果，此时由于2个目标速度和加加速度相同，其交叉项重合在一起，另外2项为自聚焦项，与单目标结果相同。图3g)为SKT结果，此时自聚焦项和交叉项的走动都得到了校正，能量落于同一距离单元。图3h)为积累结果，目标A和目标C都能得到积累，由于加速度不同位于不同的调频斜率单元，同时交叉项也得到积累但是有非常明显的扩展，这主要是因为交叉项类似于关于慢时间的线性调频信号且带有中心频率，若此种情况下用TRT-SKT-LVD算法，则会积累出3个尖锐峰值，无法分辨出交叉项和目标。

图3i)～l)为目标A、目标B和目标D的积累过程，可以验证多目标的检测性能。图3i)为脉冲压缩结果，3个目标都发生了明显的距离走动。图3j)为TRT结果，此时产生了4个交叉项和3个目标的自聚焦项。图3k)为SKT结果，此时自聚焦项的弯曲得到了校正，而交叉项依然存在走动。图3l)为积累结果，目标A、目标B和目标D都能得到积累，交叉项得到抑制。另外，目标D的积累说明在匀加速运动下，该算法也同样能实现积累，且在目标具有相同RCS条件下积累峰值更高。

由图3的仿真结果可以看到，本文所提方法对于多目标的检测具有很好的效果，目标之间对相参积累结果的影响很小，积累得到的峰值明显且尖锐。

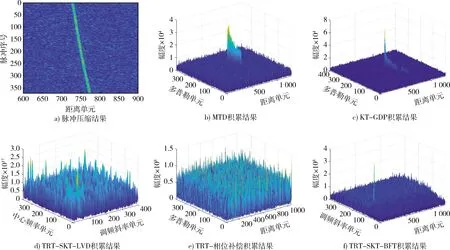
图2 几种算法的相参积累性能Fig.2 Coherent accumulation performance of several algorithms

表2 多目标运动参数Table 2 Multi-target motion parameters

4.4 积累时间要求

对机动目标进行相参积累时，积累时间是评价相参积累算法的重要指标，而相参积累时间T=MTr主要取决于脉冲积累个数和脉冲重复周期，当脉冲重复周期固定时，只与脉冲积累个数有关。为了说明不同脉冲积累个数对相参积累算法的影响，本小节作出相应简单仿真。雷达系统参数如表1设置，目标参数设置如表2目标A设置，仿真结果如图4所示。从图4中可以看到，在信噪比为-23 dB时，可取得脉冲积累个数选择较多，但是当信噪比为-24 dB时，脉冲积累个数为370时最合适，且不管高于或者低于此数值时，检测概率都降低较快。