基于区域分割的大靶面单目视觉测量技术

2020-05-18马晓东张吉旋

兵器装备工程学报 2020年4期

张杰,马晓东，张吉旋

(中国飞行试验研究院，西安 710089)

根据系统中使用的视觉传感器(测量摄像机)的数量，传统的光学测量可以简单地分为单目视觉测量、双目视觉测量以及多目视觉测量[1]。为提高测量精度，增加空间约束关系，一般采用双目视觉测量为主，通过目标在两个摄像机上的成像关系计算其空间坐标。单目视觉测量是指采用一台视觉传感器获取被测目标空间位置关系，其系统简单、成本低、易实现，在二维位置测量或准三维位置测量中使用较多。根据CCD摄像机的特点，在进行摄影测量时，应尽量使CCD成像面与被测量平面平行，但在实际的应用中，物象平行是很难达到的。

单目视觉用于二维位置测量时，因为摄像机中心位置靠近光学中心，成像畸变小、标定精度高，可以在小目标测量中获取较高的靶面测量精度[2]。在大目标平面位置测量中，光学系统覆盖面积大，图像边缘严重畸变。因此，如何提高大视场相机在单目视觉测量中的标定精度和测量精度一直是单目视觉研究的热点和难点。

大视场单目视觉测量系统构建中需要大型高精度2D或3D靶标进行标定与数据分析。这种高精度靶标对精度控制、安装使用以及后期的维护有很高的要求，需要耗费较多的人工成本。所以，探索一种新的大靶面视场的标定方法显得尤为重要。本研究根据摄影测量原理，在完成摄像机标定的基础上，对大靶面进行分割，将分割的小平面与标定结果相对应，实现了平面内物体的位置的测量。

1 摄像机的标定

摄像机的标定是视觉测量系统的重要组成部分。传统的标定方法所产生的误差，会随着视场的增大而增大。通过建立大靶面视场模型，并对摄像机的畸变特性以及待测参数在视场内不同区域的变化特点进行分析。在进行摄像机畸变参数标定的基础上将大靶面拆分为很多小的靶面，利用透视变换模型对拆分的小靶面逐个标定，根据几何对应关系把标定好的小靶面组合起来从而实现对摄像机大视场的标定[4]。

对平面中任意一点坐标进行计算时，需要对摄像机进行标定图像中任意一点畸变后的坐标为(xd,yd)，理想点与畸变点之间的关系为[5]：

(1)

式中：k为畸变系数，采用张正友图像标定算法可以得到需要的畸变系数。

在视觉测量中，经摄像机拍摄成像后，将三维目标信息立体图像以二维平面图像进行显示，必定存在数据信息的丢失[6]。在实际测量中，假设图像坐标(ui,vi)和目标平面上的原始坐标(xwi,ywi,zwi)。两者投影的不均匀对应可以描述为[7-9]：

(2)

其中：Zc为该点深度信息即摄像机坐标系下光轴所在坐标，f/dx、f/dy、u0、v0为摄像机内参，R、T为相对位姿参数，经如图1所示坐标转换，可得：

图1 坐标系变换

其中本文中选定点在同一靶面且满足zwi=0，故式(2)可变换为：

(3)

将式(3)变换展开可得：

(4)

由式(4)可得：

zc=r31xwi+r32ywi+tz

(5)

将式(5)代入式(4)，可得：

(6)

扩充到n个点，这些点像素坐标及世界坐标均已知，联立式(6)并将其改写为Ax=b的形式可得[10]：

(7)

当n≥4，式(7)有唯一解，为[11]：

x=(ATA)-1ATb

(8)

根据以上公式推导，在大靶面的标定过程中通过获取同一平面上的4个点(8个数据)，根据式(8)计算可得到R、T相关位姿参数信息，完成单目视觉大靶面平面位置测量系统的标定。

2 区域分割算法研究及实现

所谓图像分割，主要指的是根据灰度、颜色、纹理和形状等目标图像自身的特征，把图像划分成若干个互不交迭的区域，并使这些特征在同一区域内呈现出相似性，而在不同区域间呈现出明显的差异性。在本文的研究中，图像分割的作用是将大视场的标定问题转化到多个小视场内解决，这样就避免了大视场光学成像系统成像边缘畸变过大导致失真的问题。

2.1 现有区域分割算法

图像分割算法常用的主要有3种，分别是基于阈值、边缘和区域对图像进行相关处理。顾名思义，阈值法主要需要是按照某个准则函数来求解最佳灰度阈值，根据图像的灰度特征来将其分到合适的类别中。边缘法则是根据边缘线中的特征突变信息，具体实现可利用图像与模板进行卷积来完成。区域法中最常见的算法为分水岭算法，是基于拓扑理论的数学形态学的分割方法进行。

基于边缘的区域分割算法中，传统的canny算法[12]依旧是由边缘检测和连接边缘形成边界两部分组成。首先对图像进行平滑，采用一维零均值高斯滤波器进行卷积操作，其中滤波器函数为：

(9)

接下来需要从水平和垂直两个方向，通过一阶偏导的有限差分，采用2×2大小的模板，计算出图像的梯度幅值和方向，计算公式如下：

(10)

最后通过设定高、低阈值，通过与阈值比较确定图像的边缘[13]。

经过改进的canny边缘检测分割算法中，对平滑过程中的滤波函数进行引导，代替原始的高斯滤波，或借鉴不同的边缘检测算子，对边缘的梯度进行改进计算，以便能够使边缘定位更加准确。同时，阈值的选择也十分重要，根据图像自适应选取，可以提高图像的信噪比，对后期进一步进行图像处理有很大的促进作用。

2.2 线扫描激光器区域分割

在本文的研究中，线扫描激光器有很好的准直性，如图2所示，实验所用线扫描激光器在10 m内的误差为±1 mm，对标定产生影响较小。

利用线扫描激光器对待测区域进行逐行或者逐列扫描，结合摄像机进行等时间间隔成像，获取多个单根激光线的图像。扫描过程中，摄像机处于静止状态，最后将多幅图像进行合成即可完成大靶面的高精度区域分割，形成一副完整的扫描图。

最终单根激光线图像的叠加，本质上就是每一组对应点像素值的求和。灰度值越高，图像越趋近于白色，灰度值越低，图像越趋近于黑色。进而叠加的图像越多，图像就越白，线激光器的颜色就会被白色取代。因此，需要对待叠加的图像进行处理，提高图像的对比度，将图中的背景设置为黑色(像素值为0)，消除灰度值叠加带来的影响。

图2 线扫描激光器对大靶面进行区域分割

2.3 区域分割测量系统

基于区域分割的图像处理技术可分为3个步骤进行，首先对采集到的图片进行滤波，滤除噪声干扰。滤波后的图像如图3所示。

图3 滤波后的图像

本文用线扫描激光器把5 000 mm×2 200 mm的视场分割成多个连续的400 mm×400 mm矩形区域，对摄像机经过透视变换进行标定。

对实验中的每张图片来说，其光照强度不同，阈值也就不同。将其RGB色彩空间转换为HSV空间，进行重复多次试验，确定出在HSV空间提取线激光的最佳阈值范围为0.38～0.14，阈值随光照变强而逐渐减小。所以要根据图像像素值的不同选取不同阈值的累加器。

激光线准直性好，且待处理图像中的背景噪声少，可用霍夫直线检测算法提取激光线特征。所谓直线检测，即对于直角坐标系中的任意一点A(x0,y0)，经过点A的直线满足y0=kx0+b(k是斜率，b是截距)。但这种坐标系下，会出现一种特殊情况，那就是k是无穷大时，无法表示直线方程。此时，将坐标系换为极坐标系，根据对偶性将图像中的像素点映射到参数空间下一条正弦曲线,使用直线的法线表示:l=xcosθ+ysinθ，其中-D≤l≤D,-90°≤θ≤90°，θ为与正x轴的夹角,D是图像对角线最大距离[14]。这就是霍夫变换直线检测的基本原理。

设置一个合适的门限值，将累加器中累计值小于所设定门限的点归零。图像中低于所设门限值的点与图像中的线扫描激光器成像直线没有直接的对应关系。查找霍夫变换累加器，用累加器中最大累计值标记该点，将其余区域设置为零，继续查找剩余图像，并记录下一个点，直到霍夫变换累加器中的所有累加值都设置为零。没有置零的点就是需要提取的直线上的点[14]。将所有的非零点连接起来，记录检测结果，如图4所示。

图4 检测结果

最后，将所有采集到的图像处理后叠加到一起的效果图如图5所示。扫描区域需要覆盖或大于整个测量靶面，从图5中可以看出，除红色的激光外，所有区域均为黑色，说明本文区域分割算法对于大靶面的处理效果显著。

图5 线扫描激光器分割的网格

3 实验结果及分析

在对整个靶面进行区域分割后，需要对视场内的某一点的空间位置进行处理定位。首先对图像进行处理，提取出目标在图像中精确的坐标位置，根据生成的激光网格，找出这个点对应的小区域，最后按照标定的数学模型以及物象对应关系计算出实际目标点的空间位置。

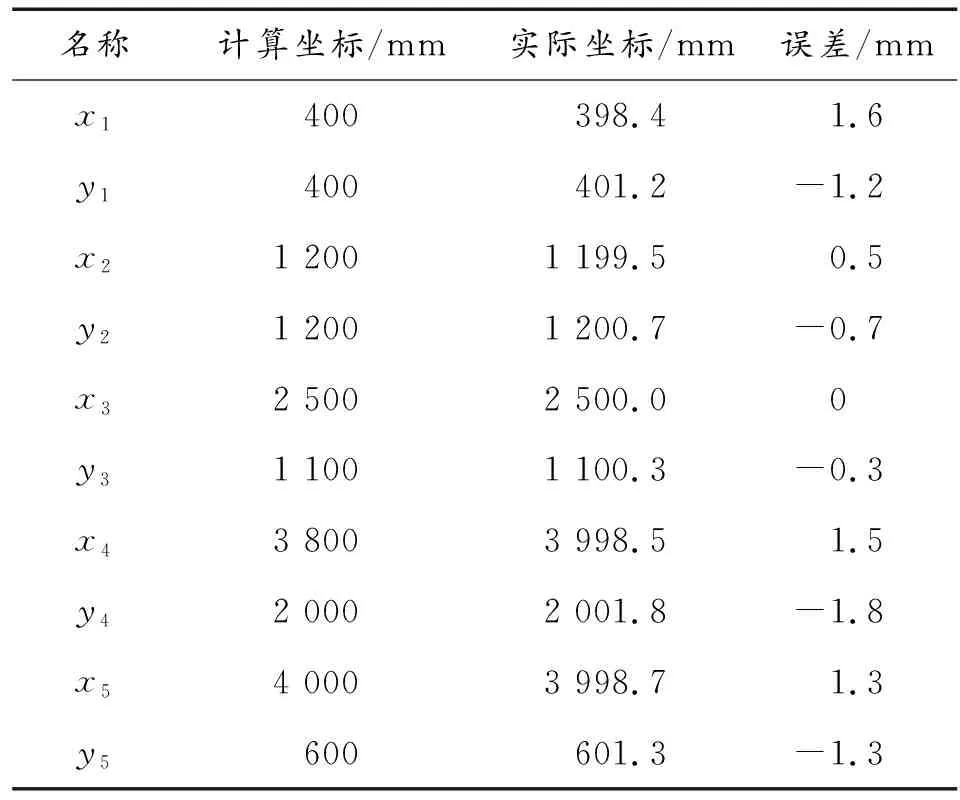
目标所在位置如图6(a)所示，首先对图像中捕捉到的目标进行图像坐标提取，得到目标的中心点坐标后，找出它所属的小分割区域。如图6(b)所示，在这个小区域内求得点的位置，根据标定时线激光扫描的宽度以及高度，就可以将这个点还原到整个大靶面内的位置，从而得到其在靶面中的精确坐标。实验中选取50组点进行精度验证，所得部分结果如表1所示。

图6 目标与解算区域的关系

名称计算坐标/mm实际坐标/mm误差/mmx1400398.41.6y1400401.2-1.2x21 2001 199.50.5y21 2001 200.7-0.7x32 5002 500.00y31 1001 100.3-0.3x43 8003 998.51.5y42 0002 001.8-1.8x54 0003 998.71.3y5600601.3-1.3

从计算结果可以知道，列出的5个目标点计算精度均小于2 mm。误差分布范围在测量平面的中心区域精度最高，边沿区域精度有所下降，总体精度能够满足大靶面位置测量要求。