适用于光伏发电直流并网的DC-DC变换器

任向阳，周 攀，戴朝波

(1.广西电网有限责任公司南宁供电局，广西 南宁 530022；2.国网北京市电力公司昌平供电公司，北京 昌平102200；3.先进输电技术国家重点实验室(全球能源互联网研究院有限公司)，北京 昌平 102209)

0 引言

太阳能作为一种新型的绿色可再生能源，是未来人类重点开发利用的新能源之一。过去几十年来，太阳能光伏发电也由最初的“屋顶计划”发展到今天的大规模并网，这也是光伏发电未来发展的主要方向[1]。当前，光伏并网主要是将光伏组件产生的直流电能通过逆变器转换成交流电能送入电网，实现并网发电。

未来以光伏发电为代表的可再生能源在国家政策的推动下将得到大规模的推广应用，分布式新能源的就地消纳会成为未来配电网的重要特征。未来配电网中，变频电器、电动汽车充换电站、数据中心以及新型电子类终端等新型负荷不断涌现，负荷类型趋于多样化。

国家电网公司已在张家口启动张北可再生能源柔性直流送出与消纳示范工程，针对高渗透率可再生能源的接入和敏感负荷的广泛应用，对配电网的潮流控制，交直流接入能力、电能质量隔离控制以及优质供电能力所带来的问题，国家电网公司提出了柔性变电站的概念。柔性变电站可同时引出直流馈线和交流馈线，满足用户对交、直流不同电能形式的用电需求。通过柔性变电站交、直流馈线分别供电，可省略部分变换环节和变换装置，使得配电网结构简单，控制更加灵活、损耗降低，因而适用于负荷多样化且集中的区域。

本文提出了一种适合光伏发电直流并网的组合型DC-DC变换器，首先根据实际工程要求，对电路参数进行了设计；然后建立小信号模型对影响变换器输出电压及模块间均压因素进行了分析；最后提出了一种移相控制和均压控制策略。

1 并网拓扑结构选择

图1为光伏发电直流并网接入柔性变电站示意图，图中MPPT为最大功率点跟踪(maximum power point tracking)。

图1 光伏发电经DC/DC变换器接入柔变直流母线Fig.1 Photovoltaic power generation connect the DC/DC converter to DC bus of flexible substation

在直流DC-DC变换器中，传统的Boost电路因其具有采样和控制电路简单，成本低廉等优点而广泛应用于光伏发电最大功率跟踪控制中。而在其他应用场合，有时为了实现电压高增益，需要把Boost电路开关管的占空比调节到接近于1的极限值。极限占空比制约了占空比变化区间调节范围，导致动态特性较差。因此，传统Boost电路不适合应用在高增益高效率变换场合[2]。

Mustansir H．Kheraluwala 最早提出了隔离式双向全桥(dual-active-bridge, DAB) DC-DC 变换器的拓扑结构[3 -7]，DAB式 DC-DC 变换器可实现直流电压变换、功率双向流动、故障隔离等功能。由于光伏发电并网功率是单向流向，单向全桥无论是从经济上来说还是从控制角度来看都更适合用于光伏发电直流电压变换[8]。

文献[9]提出用隔离型DC-DC全桥变换电路为光伏发电模块级联终端，输出端器件为二极管整流结构，形成多二极管串联电路。然而，串并联绝缘栅双极型晶体管 (insulated gate bipolar transistor, IGBT)，器件间的均压和均流问题却又是个难题。若采用多个DC-DC变换器单元串联的方式，可减小各变换器子模块中开关器件的电压应力，适合高电压的应用场合；而采用多个 DC-DC 变换器单元并联的方式，可减小各变换器子模块中开关器件的电流应力，适合大电流场合[10]。目前，移相全桥电路是国内外应用非常广泛的软开关电路。与传统的全桥硬开关电路相比，移相全桥电路仅需在隔离变压器原边侧串联一个谐振电感，就可以实现功率开关管的零电压开通。因此，可以选用移相全桥ZVS变换器为基本单元来构成输入侧并联输出侧串联组合型DC-DC 变换器，移相全桥电路及其主要工作波形分别如图2—3所示，组合型DC-DC 变换器如图4所示。其中：Uin表示输入电压；Tj(j=1,2,3,4)表示功率开关管；Dj(j=1,2,3,4)表示功率开关管的反并联二极管；Cj(j=1,2,3,4)表示功率开关管的寄生电容；Lr表示谐振电感；DRj(j=1,2,3,4)表示输出整流二极管；Lf表示滤波电感；Cf表示滤波电容；R表示等效负载。T1和T3的驱动信号超前T2和T4一定相位，T1和T3构成超前桥臂，T2和T4构成滞后桥臂。分析之前，先做出如下假设:

图2 移相全桥变换器Fig.2 Phase shift full bridge converter

图3 移相全桥变换器主要波形图Fig.3 Main waveforms of phase shift full bridge converter

图4 组合型DC/DC变换器Fig.4 Combined DC/DC converter

1) 所有元器件均为理想的。

2)C1=C3=Clead，C2=C4=Clag。这里，Clead为超前桥臂的寄生电容，Clag为滞后桥臂的寄生电容。

3)Lf≫Lr/K2，K为变压器变比[11]。

2 工程参数计算

工程设计要求：光伏发电功率P=2.5 MW，输入电压Uin=750 V(±5%)，输出电压Uo=±10 kV。

根据工程设计要求，选用20个移相全桥电路通过输入侧并联输出侧串联级联成组合DC-DC变换器，每个模块传输额定功率125 kW，控制每个模块输出电压为1 kV，输出端等效额定负载8 Ω。

2.1 隔离变压器变比计算

假设副边最大占空比Demax=0.85，二极管导通压降UD=1.5 V，输出滤波电感压降ULf=2 V，变压器副边最低电压为

(1)

原副边变比为

(2)

为了减小变压器副方整流二极管的反向电压，降低变压器原方开关器件上的电流应力，并有效提高变压器的利用率，高频变压器的额定变比应该尽量选小一些。因此，选定变压器变比K=0.6。

2.2 超前桥臂电容计算

在超前桥臂开通过程中，谐振电感Lr与折算到原边的输出滤波电感Lf串联，用Lf和Lr中的能量是来实现超前桥臂ZVS。一般来说，Lf很大，所以在超前桥臂开通过程中，可以认为变压器原边电流近似不变，等效于1个恒流源。因此，为了实现超前桥臂的零电压开通，必须使T1和T3驱动信号的死区时间满足以下关系

(3)

由上式容易看出，当输出电流I0变小时，C3放电到0的时间将会变长，即超前桥臂在轻载时可能失去零电压开关条件。因此，选择电容C1和C3要依据超前桥臂死区大小和要求实现零电压开关的负载范围来确定，考虑在最高输入电压，也就是最难实现零压开通时来确定。

实际上，大功率装置设备中，由于采用IGBT作为开关器件，死区时间不宜设置过小，一般为2.0～2.5 μs，设置超前桥臂死区时间为2.0 us。考虑变换器在大于20%额定负载时都能实现零电压开关，即IP大于41.6 A时能实现零电压开关，输入最高电压为787.5 V，则有

(4)

2.3 滞后桥臂电容计算

在滞后桥臂开关过程中，变压器副边是短路的，此时用来实现ZVS的能量只是谐振电感中的储能，因此滞后桥臂实现ZVS比较困难。

当滞后桥臂工作时，变换器谐振电感Lr和开关器件的并联电容C2、C4谐振，A点电位由Uin逐渐减小，当低于低电位时，D2导通，此时开通T2，则T2实现零电压开通。由此可见，若要实现滞后桥臂的零电压开通，必须满足以下条件:

(1) 串联谐振电感储能大于滞后桥臂谐振电容储能，即

(5)

忽略变压器寄生电容CTR，简化可得：

(6)

(2) 在滞后桥臂开通时，原边电流近似为恒定。滞后桥臂的并联电容满足下式

(7)

(3) 滞后桥臂开关的死区时间应小于或等于四分之一的谐振周期，即

(8)

在这3个约束条件及滞后桥臂死区时间2.0 μs和ZVS软开关41.6 A电流条件下，可以选择合适的谐振电感Lr和谐振电容Clag。由于串联谐振电感和开关器件并联电容均不宜过大或过小，故谐振电感应与开关管并联电容协调确定。

在上述约束条件下，有：

(9)

代入参数计算滞后桥臂电容得，Clag<5.28×10-8F。这里选取Clag=40 nF，根据上式得到串联谐振电感Lr≥2.03×10-5H。

2.4 输出滤波电感电容的设计

工程设计中，一般要求输出滤波电感电流的脉动量ΔI为额定输出电流的20%。也就是说，要使输出电流为额定电流的10%×Io的情况下，流过输出滤波电感上的电流保持连续。所以，上式中的Io_nom可取10%。全桥DC-DC变换器副边整流后得到的方波电压频率为2fs，即fLf=2fs。为了保证输出滤波电感电流的最大脉动量ΔImax不超过最大输出电流的20%，则输出滤波电感为

(10)

式中：Uo=1 kV；Io=125 A；fs=3 kHz；Uin_max=787.5 V；ULf=2 V；UD=1.5 V；K=0.6，代入参数计算得Lf= 1.56 mH。

输出滤波电容的容量大小应该根据电源对输出电压纹波Uo-pp的要求来设计。输出滤波电容的电容量Cf可依据以下公式计算得到:

(11)

要求输出滤波电容将电压波动限制在较小的范围，波动允许幅值取Uo-pp=100 mV。这里，fcf=2fs，代入上式并代入参数计算得Cf=5.2 mF[12-13]。

3 小信号建模分析

以2个基本模块单元组合变换器为例，建立组合变换器的小信号模型如图5[14-15]。

图5 两模块组合全桥变换器小信号模型Fig.5 Small signal model of two-module combination Full-bridge converter

根据小信号模型推导副边有效占空比De为

(12)

稳态时，根据输入输出功率平衡有(不计损耗):

(13)

因为输出侧串联，所以有Io1=Io2=Io，代入式(13)可得

(14)

由式(12)(14)可得

(15)

把De1Uin/K=Uo1和De2Uin/K=Uo2，代入式(15)可得

(16)

由式(16)可见，两模块参数匹配且原边占空比相同时，有Lr1=Lr2、Lf1=Lf2和D1=D2，根据式(14)(16)有：Uo1=Uo2；Io1=Io2。

由式(16)可知，影响均压的因素有谐振电感、滤波电感、开关管和整流二极管的导通压降、原边占空比等。

3.1 谐振电感不同对均压影响

假设两模块间其他参数完全相同，设置Lr1=20uH,Lr2=19uH，仿真结果如图6。仿真结果表明：谐振电感不一致会导致各模块输出电压的不均衡，且谐振电感大的模块的输出电压低。这是因为两模块的原边占空比相等时，谐振电感较大的模块占空比丢失大，副边所得到的有效占空比较小，导致了该模块输出电压较低。

图6 谐振电感不同时输出均压情况Fig.6 Impact on voltage among modules due to the differences of resonant inductors

3.2 滤波电感不同对均压影响

假设两模块间其他参数完全相同，设置Lf1=1.56 mH,Lf2=1.46 mH，仿真结果如图7。仿真结果表明：输出滤波电感影响模块间输出电压均衡，输出滤波电感小的模块输出电压的纹波较大，输出滤波电感大的模块输出电压纹波较小。

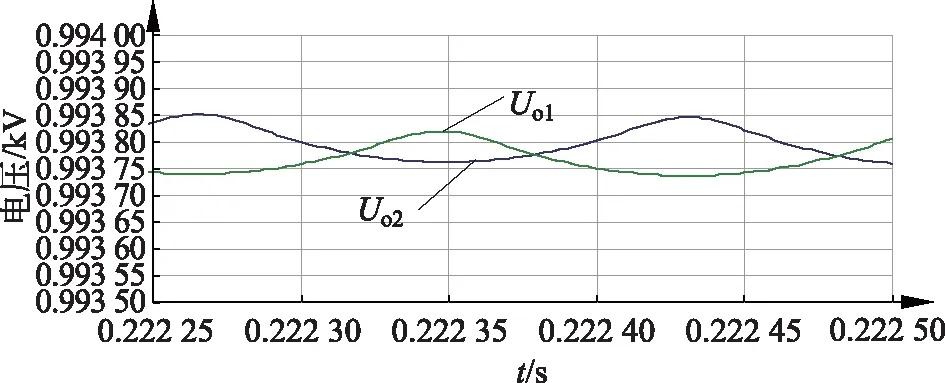
图7 输出滤波电感不同时输出均压情况Fig.7 Impact on voltage among modules due to the differences of filter inductance

3.3 导通压降不同对均压影响

同样假设模块间其他参数完全相同，而在模块2的整流二极管上串联1个0.15 Ω电阻，仿真结果如图8。仿真结果表明：模块中整流二极管的导通压降会影响输出电压均衡,这是因为导通压降大的模块对应副边整流后得到的电压较低，因此整流二极管或开关管导通压降大的变换器模块输出电压较低。

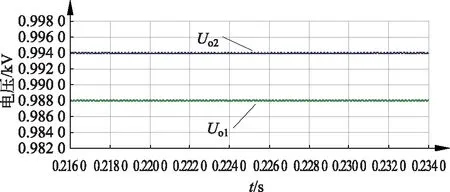
图8 导通压降不同时输出均压情况Fig.8 Impact on voltage among modules due to the differences of conduction pressure drop

3.4 滤波电容不同对均压影响

由式(16)可知，滤波电容对占空比丢失没有影响，也不影响模块间电压差异大小。实际电路中，输出滤波电容一般采用容值较大的电解电容，但其实际的容值与标称值大小之间存在一定的差异，因此两变换器模块输出滤波电容的容值不可能完全相同。假设两模块间其他参数完全相同，设Cf1=5.2 mF，Cf2=5.0 mF，仿真结果如图9。仿真结果表明，输出电容不一致不影响均压。

图9 输出滤波电容不同时输出均压情况Fig.9 Impact on voltage among modules due to the differences of filter capacitance

4 全桥变换器控制策略研究

4.1 闭环控制策略

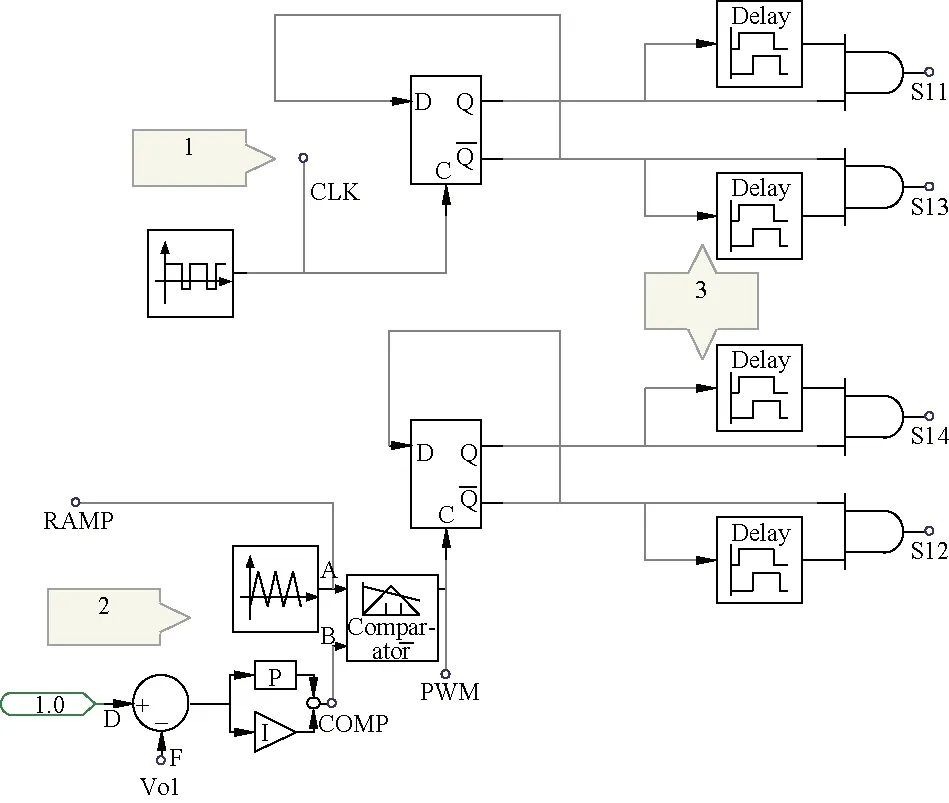
图10 脉冲驱动模型Fig.10 Pulse drive model

图11 功率开关管驱动波形Fig.11 Drive waveforms of power switch tube

运用如图10的脉冲驱动模型来驱动移相全桥的4个功率开关管， 4个功率开关管的驱动波形如图11所示，脉冲驱动控制主要波形如图12所示。

为验证控制策略的有效性，设定输入电压在仿真时间0.5 s时由750 V阶跃到730 V，0.75 s时又恢复到750 V，仿真输出电压变化波形图如图13所示；输出等效负载在仿真时间0.5 s由8 Ω阶跃到40 Ω时，仿真输出电压变化波形图如图14所示。仿真结果表明，无论是输入电压发生突变还是负载发生突变，输出电压都能很快的迅速稳定在1 kV。

4.2 均压控制策略

图12 单模块控制相关波形图Fig.12 Relevant waveforms of single module control

图13 输入电压阶跃变化时输出电压变化波形图Fig.13 Impact of input voltage step change on output voltage

图14 负载阶跃变化时输出电压变化波形图Fig.14 Impact of load step change on output voltage

图15 均压控制框图Fig.15 Control block diagram of sharing output voltage

控制框图如图15所示，控制策略有19个输出均压环和1个共用的输出电压环组成。组合系统中前19个模块中各模块的输出电压值与系统总输出电压值的1/n经过比较器后进入比例积分(proportional integral, PI)调节输出；系统总输出电压与参考电压比较后经过PI调节。前19个模块将共用输出电压调节输出值与每个模块各自输出均压调节值做差值比较后，再与三角波交截产生各自模块的驱动信号，第20个模块的驱动信号是通过输出电压环调节输出信号与各个模块均压环调节输出信号累加后再与三角波交截形成。

设置差异性参数如下：第3个模块的谐振电感为19 μH；第7个模块滤波电感为1.46 mH；第12个模块的整流二极管上串联1个0.1 Ω电阻。对20个模块级联组合变换器仿真分析，总输出电压仿真结果如图16所示，各子模块输出电压仿真结果如图17所示，均压控制仿真结果如图18所示。仿真结果表明：在级联组合变换器模块间参数存在细微差异时，采用上述均压控制时，能够维持模块间输出电压均衡。

图16 20模块组合变换器总输出电压波形图Fig.16 Total output voltage waveform of 20 module combination converter

图17 20模块组合变换器各模块输出电压波形图Fig.17 Output voltage waveform of each module of 20 module combination converter

图18 均压控制仿真波形图Fig.18 Simulation waveform of sharing voltage control

5 结论

本文提出了一种基于移相全桥电路，采用输入侧并联输出侧串联的组合DC-DC变换器拓扑，能够实现低电压输入、高电压输出，适用于光伏发电直流并网系统。通过对两个移相全桥电路级联建立小信号模型，分析了影响模块间输出均压的因素，提出了一种简化控制策略及均压控制策略。在PSCAD/EMTDC仿真平台验证了影响模块间均压的因素，并验证了所提控制策略的有效性。