新能源接入的多时间尺度协调响应调度模型

胡兵轩， 覃禹铭

（贵州电网有限责任公司遵义供电局，贵州遵义563000）

0 引 言

近年来，新能源凭借其清洁、无污染、可再生等诸多优点，在电力发电领域保持着较高的发展势头［1-2］。但同时其出力不确定性、波动性又制约着新能源的高效利用。当主动配电网中新能源的渗透率比较高时，会在一定程度上影响配电网中可调功率资源出力的调度以及备用容量的选择［3-4］。国内外学者针对含有大量新能源的主动配电网协调调度问题进行了大量的研究，并取得了一定成果。文献［5］中按照单位调节成本对主动配电网中的可调资源进行了动作优先级设置，构建了多目标优化函数求解出各可调资源的协调出力情况。文献［6］中根据随机机会约束建立了含有风力发电机组的配电网最优潮流调度模型。但上述文献未考虑分布式电源等可调资源出力的不确定性。文献［7］中提出了新能源出力具有随机性的概念，并建立了“源荷储”调度模型，但未考虑柔性负荷以及储能装置出力的不确定性。

模型预测控制技术根据被控系统的动态性能进行闭环控制，能够有效克服被控系统模型的不确定性，具有良好的鲁棒控制效果，在电力系统优化控制领域发挥着越来越重要的作用［8-9］。文献［10］中为了对风力发电出力进行较高精度的预测，提出了将预测时间逐渐细分的短时间优化调度，实现了风机与传统能源的协调控制。文献［11］中首先将模型预测控制理论应用于配电网的调度优化中，实现了分布式电源与负荷的在线滚动出力优化。文献［12］中将模型预测理论与分层递推理论相结合提出了一种分层调度控制方法，来解决风机出力调度问题。上述文献虽然都考虑了可调资源出力的不确定性，但仍属于开环控制，具有较高的预测和控制误差。

本文根据主动配电网中可调功率资源的不同特性，提出多时间尺度协调调度优化模型。首先建立了分布式电源、柔性负荷和储能装置预测模型来降低其出力不确定性对调度建模的影响。然后以当前调度成本最低为优化目标，建立日前和日间优化调度模型；在MPC滚动优化中引入反馈校正环节实现闭环实时反馈优化调度，降低可调功率资源预测误差和不确定扰动对优化结果的影响。最后以改进IEEE33节点仿真算例为例进行仿真验证。

1 MPC控制原理

模型预测控制是一种闭环模型优化控制，适用于强非线性复杂系统，并且能够克服被控系统的扰动性和不确定性，其控制思想的核心是利用系统当前的测量量和预测模型通过一定的优化算法得到一段预测周期内的最优控制策略，并根据系统下一时段的实际值进行反馈校正重复这一优化过程［13］。

图1所示是模型预测控制原理图，纵轴表示被控系统的输出，横轴为时间序列。图中：Δu（k）表示k时刻系统的控制增量；Nc表示控制时域步长；Ny表示预测时域步长，并且Ny≥Nc。在k时刻，利用当前的测量数据根据预测模型求得Nc控制步长内的控制变量增量：

从而使得被控系统指标在预测时域k＋Ny内满足要求。虽然得到的控制变量增量序列有Nc，但在实际控制中只执行第1个控制增量Δu（k），在k＋1时刻利用最新的测量数据重复上述过程。

图1 MPC控制原理图

2 基于MPC的配电网协调调度模型

高渗透新能源的大量接入，使得配电网传统的调度方法已经不适合主动配电网的调度要求，并且随着分布式电源数量的增多，在现有主动配电网通信水平下无法做到对各个光伏电站、风电变化的实时响应。

本文基于模型预测理论提出多时间尺度协调优化调度模型；长时间尺度包括日前优化调度和日间优化调度；短时间尺度为实时反馈优化调度。3个优化调度阶段的关系如图2所示。

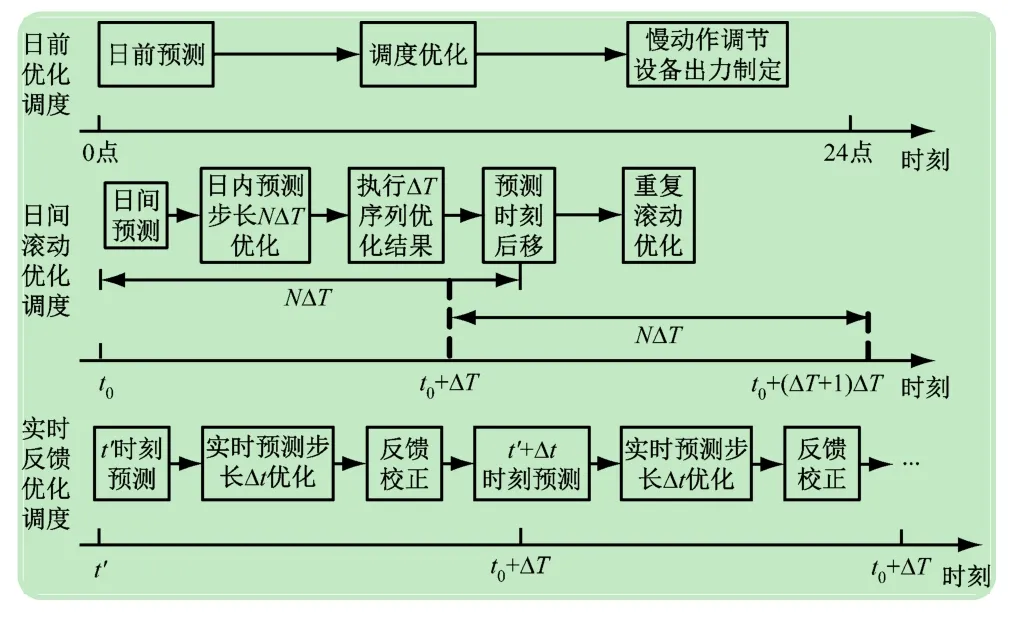
图2 基于模型预测的调度优化模型框架

2.1 长时间调度优化模型

2.1.1 日前优化目标函数

日前优化调度是根据主动配电网中各设备的日前状态信息进行的优化控制，其优化调度周期为1 h。主动配电网中的电力电容器组、有载调压变压器（On Load Tap Changing，OLTC）等设备的动作调节速度一般都比较慢，不适合短周期的滚动优化和实时反馈控制，故需要在日前优化中确定这些慢动作设备的动作量。日前优化调度的目标函数是在保证主动配电网各项指标合格的前提下，系统的调度成本。并且为了限制在一定时间段内有载调压变压器和并联电容器组频繁动作，本文根据有载调压变压器和并联电容器组单位调节代价，将其动作次数约束转化成控制成本性问题。具体优化目标函数如下：

式中：T1表示日内调度优化的周期；Cgrid和Pgrid分别表示当前时刻主动配电网与主电网交换功率单位调度成本和交换功率；CDGi、Cloadi、Csti、COLTCi、Cci分别表示第i分布式电源有功和无功功率调度调节代价、主动配电网柔性负荷（可中断供电）调度成本、储能装置功率调度成本、有载调压变压器调度成本和并联电容器组调度成本；ng、nl、ns、nO、nc分别表示可调分布式电源、配电网柔性负荷、储能装置、有载调压变压器和并联电容器的个数；αi和βi均表示配电网需向第i个柔性负荷支付补偿成本系数；ΔPloadi表示调度时第i个柔性负荷的功率改变量；λst表示调度储能装置时的单位成本系数；Pst表示调度时储能装置充放电功率改变量；ai、bi、ci分别表示分布式电源调度单位成本系数；PDGi表示调度时分布式电源有功功率增发量；TK.i和NC.i分别表示第i台有载调压变压器可调节分接头的档位和并联电容器组投放数量；ΔCT、ΔCQ分别表示有载调压变压器单位调节代价和并联电容器组单位调节代价。

2.1.2 日间优化目标函数

日前优化调度中分布式电源、柔性负荷以及储能装置的预测步长比较长，影响这些设备预测的不确定因素增加时会导致预测的精准度大大降低，因此需要缩短预测步长。日间优化调度的优化周期为ΔT，其预测步长为MΔT。根据分布式电源、柔性负荷和储能装置的预测结果进行优化，优化的目标函数为当前系统调度成本最低。虽然日前优化调度的预测步长为MΔT，但根据MPC的控制原理只执行第一序列控制量，然后预测时间后移，重复滚动优化。日间优化调度的目的是制定除慢动作设备外其余可调设备的动作量，而慢动作设备的动作量按照日前制定的执行。其具体优化目标函数为：

2.2 短时间调度优化模型

日间优化调度虽然已经降低了外界不确定因素对分布式电源以及柔性负荷的影响，但这种控制方式仍属于开环控制。实时反馈优化调度以比ΔT更短的时间Δt为调度周期，对可调功率进行超短期时间预测，并将当前t0时刻系统的实际输出量设定为初始值，进行反馈预测，从而构成闭环控制来校正模型预测的误差，提高调度精度。实时反馈调度优化的目标是当前时刻主动配电网可调功率资源的出力调整量最小，从而减小可调功率资源的波动。其具体二次优化目标函数为：

式中：u0（k）表示当前时刻可调功率资源的初始测量值； （k＋i｜k）表示优化阶段可调有功资源调整量；u¨（k＋i）表示t＋ i时刻系统可调功率资源出力值，即日间优化调度求得的各可调功率资源的出力。

实时反馈调度优化中的可调功率资源包括系统联络线功率、柔性负荷、分布式电源以及储能装置，则：

式中：Δu（k＋i｜k）表示k时刻预测出k＋i时刻各可调功率资源的出力增量。

根据目标函数求得的可调功率资源优化解是Nc个控制变量增量序列

但只将控制变量增量的第1序列即Δu（k＋1｜k）下发，计算得到k＋1时刻主动配电网可调功率资源出力u（k＋1｜k），进而进行新一轮的滚动预测优化。为了降低预测优化带来的误差将当前时刻（k＋1）可调功率资源的实际出力值作为新一轮滚动优化的初始值，即：

式中：u0（k＋1）表示k＋1时刻滚动优化可调功率资源出力的初始值；ureal（k＋1）表示k＋1时刻主动配电网可调功率资源出力的实际值。

2.3 预测模型

本文针对柔性负荷、分布式电源和储能装置的特点分别建立预测模型。

（1）柔性负荷预测模型。主动配电网中的柔性负荷在短时间内的波动范围一般较小，其预测模型可以利用加权移动平均法来建立，本文采用3阶平均，则第m个负荷的预测模型为：

式中：Ploadm（k＋i｜k）和Qloadm（k ＋i｜k）分别表示在当前k时刻预测出k＋i时刻的负荷有功和无功功率；ωt表示权重值。

（2）分布式电源的预测出力模型。主动配电网中的分布式电源主要受天气的影响，波动随机性比较大，故利用自回归滑动平均法进行模型预测，第m个分布式电源的预测模型为

式中，各个变量值详见参考文献［14］。

（3）储能状态预测模型。

式中：ESOCm（k＋i-1｜k）表示基于当前k时刻测量值预测出的k＋i-1时刻储能装置状态；ηm表示储能充放电效率；ΔPEm（k＋i-1）表示k＋i-1时刻储能装置的充、放电功率；Eratem表示储能装置的总容量。

2.4 约束条件

（1）有功功率平衡约束

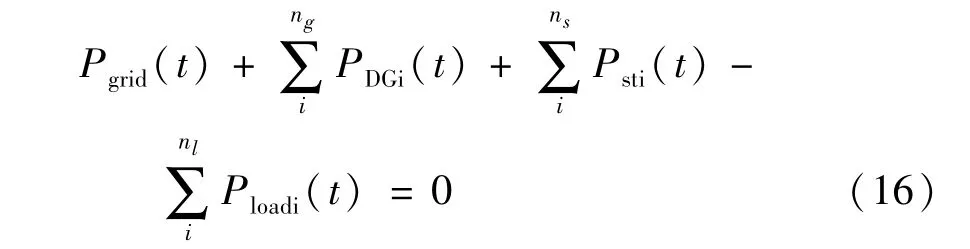
式中：主电网向配电网传输有功功率时Pgrid为正；储能装置放电时Pst为正，否则为负值。

（2）配电网安全运行约束

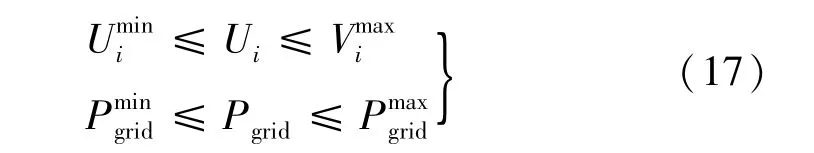
（3）分布式电源出力约束。分布式电源发出有功功率的同时也可以利用逆变器的复用特性产生一定的无功功率，但光伏发电时的有功功率和无功功率出力会受到逆变器容量的约束：

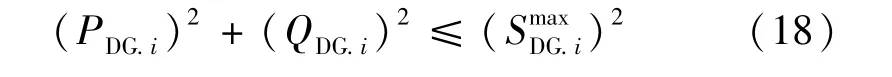
式中：PRE.i.t和QRE.i.t分别表示在t时刻第i个清洁能源发电的有功功率和无功功率。

清洁能源发电电源进行功率输出时会受到爬坡率的约束：

（4）储能出力约束。储能装置的有功功率和无功功率出力总额受逆变器容量的约束：

式中：Pch.i.t和Pfa.i.t分别表示t时刻第i个储能装置充电和放电有功功率；Qch.i.t和Qfa.i.t分别表示t时刻第i个储能装置充电和放电无功功率；表示第i个清洁能源发电的逆变器的最大视在功率。

系统中的储能装置在任意时刻只能处于充电状态或者处于放电状态，并且在此过程中储能装置存储的电量一般被限制在其电量总额的20% ～90%，故储能装置需要遵循以下约束条件：

（5）并联电容器组约束

（6）有载调压变压器约束

3 算例仿真分析

本文在Matlab仿真平台典型IEEE33节点系统中加入了分布式电源、储能装置、并联电容器组等模块，构成改进IEEE33节点配电网系统来验证本文所提的多尺度调度优化模型，如图3所示。其中各个可调设备在系统中的位置和参数如表1所示。令预测时域步长和控制时域步长相等，日前优化步长为1 h，日间优化步长为15 min，实时反馈优化步长为5 min。

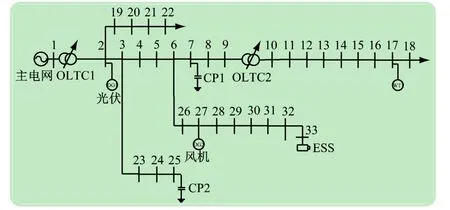
图3 改进的IEEE33节点仿真系统结构图

表1 可调设备位置及参数

如图4所示分别在日前1 h、日间15 min和实时反馈5 min优化调度的作用下，风电功率的预测值曲线图。从图中可以看出，预测步长越大风电预测值与实际出力值的误差就越大，并且实时反馈优化中的风电预测值与实际出力值的误差很小，验证了所提预测模型的正确性。

图4 多尺度下风电功率出力预测值

图5和图6所示分别为日间优化调度和实时反馈优化调度下主动配电网中部分可调功率资源的计划出力情况。从图5和图6可以看出，微型燃气轮机的有功出力成本比较低，所以几乎一直处于较高的有功出力状态中；光伏电池随着时间的推移其有功出力水平保持着增大的趋势。

图5 日间优化调度各可调功率资源出力计划值

图6 实时反馈优化调度可调功率资源出力计划值

为了充分验证本文所提实时反馈优化调度方法的精准性，将其与传统的一次预测开环优化调度方法［15］进行对比仿真，图7所示的是在两种调度方法的作用下微型燃气轮机和储能装置的计划出力情况。从中可以看出，两种调度方式下微型燃气轮机和储能装置的处理趋势大体相同，但在滚动预测优化和实时反馈校正的闭环调度优化作用，可调功率资源的出力变化比较平滑，能够有效减小可调功率资源的机械磨损，延长使用时间。

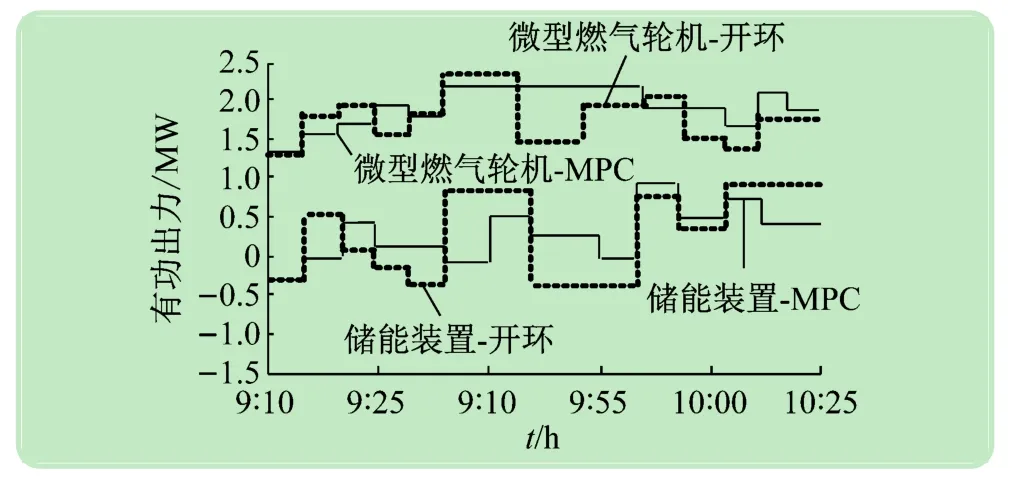
图7 两种调度方式下可调功率资源出力计划值

4 结 论

本文针对含有大量新能源接入的主动配电网中各种可调功率资源有功和无功功率的协调调度问题，结合可调功率资源出力预测精度随着预测步长的增加而逐渐降低的特性，基于MPC提出了多时间尺度功率协调调度优化模型，主要结论如下：

（1）设计日前—日间—实时反馈优化调度模型：日前优化确定慢动作设备出力值；日间优化确定快速可调资源出力计划值；实时反馈优化以日间优化出力值为参考，进行实时反馈滚动优化，提高了调度决策的准确性。

（2）根据可调功率资源特性建立了分布式电源、负荷以及储能装置的预测模型，有效降低其出力不确定性对调度建模的影响。

（3）模型预测技术通过闭环控制能够有效跟踪可调功率资源出力值，并在改进的IEEE33节点系统上验证了所提控制策略的有效性。