基于四波混频过程和线性分束器产生四组份纠缠*

余胜 刘焕章 刘胜帅† 荆杰泰2)‡

1) (华东师范大学, 精密光谱科学与技术国家重点实验室, 上海 200062)

2) (山西大学, 极端光学协同创新中心, 太原 030006)

多组份纠缠是量子信息处理的重要资源, 它的产生通常涉及到许多复杂的线性和非线性过程.本文从理论上提出了一种利用两个独立的四波混频过程和线性分束器产生真正的四组份纠缠的方案, 其中, 线性分束器的作用是将两个独立的四波混频过程联系起来.首先应用部分转置正定判据研究了强度增益对四组份纠缠的影响, 结果表明, 在整个增益区域内都存在真正的四组份纠缠, 并且随着强度增益的增加, 纠缠也在增强.然后研究了线性分束器的透射率对四组份纠缠的影响, 发现只要线性分束器的透射率不为0或1, 该系统也可以产生真正的四组份纠缠.最后, 通过研究该系统可能存在的三组份纠缠和两组份纠缠来揭示该系统的纠缠结构.本文理论结果为实验上利用原子系综四波混频过程产生真正的四组份纠缠提供了可靠的方案.

1 引 言

多组份纠缠不仅在检验基本量子效应方面具有重要作用[1], 而且在量子通信以及量子计算领域也有着广泛的应用[2−5].在连续变量量子系统中,已经有大量产生多组份纠缠的方案在理论上提出并在实验上实现[6−12].在这些方案中, 比较典型的方法是利用光学参量振荡器和线性分束器网络产生的独立单模压缩光束来生成连续变量多组份纠缠[9].此外, 另一种有效且简单的方法是在时域[13]和频域[14−16]中使用复用技术产生大规模连续变量簇态.最近, 我们课题组已经在实验上证明了热铷原子蒸气池中的级联四波混频过程可以产生多个量子关联光束[17−22], 并在理论上提出了产生真正的三组份纠缠[23]和四组份纠缠[24,25]的方案, 这种级联是基于铷原子的双L能级结构.不同于铷原子池的级联, 类原子系统能级级联的多波混频过程是基于类原子系统的N型能级结构, 这种级联不仅可以产生关联光束[26−28], 而且关联和压缩可以通过修饰场引起的相对非线性相移来控制[27].检验多组份量子纠缠时, 有很多判据可供选择[29−35].本文选择部分转置正定判据[34,35].

由于强的非线性过程、空间多模性和可产生空间分离的非经典光束等优点, 热铷原子蒸气池中的四波混频过程是产生连续变量多组份纠缠的一项有前景的技术[36].本文提出了一个基于两个独立的四波混频过程和一个线性分束器来产生真正的四组份纠缠的方案, 其中, 线性分束器的作用是将两个独立的四波混频过程联系起来.然后, 应用部分转置正定判据从理论上研究了系统的纠缠特性对强度增益和线性分束器的透射率的依赖性, 证实了该系统存在真正的四组份纠缠.此外, 为了更好地解释系统的纠缠结构, 研究了该系统中可能存在的三组份纠缠和两组份纠缠.

2 理论推导

图1(a)为由线性分束器连接的两个独立的四波混频过程的结构图.该方案可以产生四组份纠缠的关键是引入了线性分束器, 它将两个独立的四波混频过程联系起来.图1(b)为铷-85 D1线的双L能级结构, 其中, 非线性相互作用强度极大地依赖于单光子失谐D和双光子失谐d.

在四波混频过程中, 湮灭的两个抽运光子会同时转换成一个探针光子和一个共轭光子.在这里,分别用标记探针光子和共轭光子, 相互作用强度用e表示,表示相互作用哈密顿量.在无耗尽及经典抽运近似条件下, 相互作用哈密顿量可以表示为

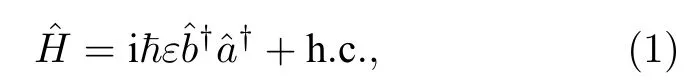
其中h.c.表示厄米共轭项.

为了方便, 我们分别用 1, 2, 3 和 4 表示光束C1, Pr1, Pr3和 C3.由 (1)式可得, 系统的输入输出关系可以写为

基于(2)式和上述分析, 本方案中的正交振幅算符和正交相位算符的输入输出关系可以表示为

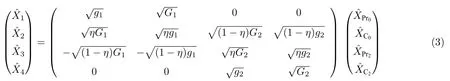
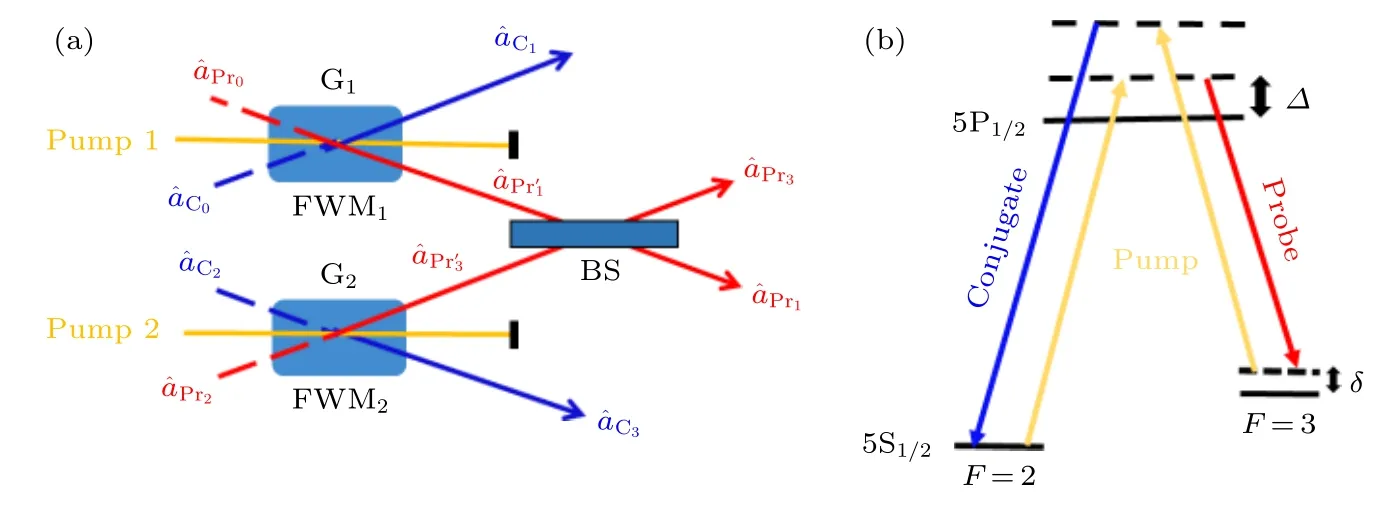
图1 产生四组份纠缠的简化图及铷-85 D1 线的双 L 能级结构 (a) C0 和 C2 是真空态注入, Pr0 和 Pr2 是相干态注入; C1 和是第一个四波混频过程产生的孪生光束, C3和是第二个四波混频过程产生的孪生光束; 光束Pr1和Pr3是光束和经过线性分束器混合后产生的; (b)铷-85 D1线的双L能级结构, D和d分别表示单光子失谐和双光子失谐Fig.1.A simplified diagram of quadripartite entanglement and an energy level diagram of rubidium-85: (a) C0 and C2 are vacuum states, Pr0 and Pr2 are coherent states; C1 and are the twin beams generated by the first four-wave mixing process, C3 and are the twin beams generated by the second four-wave mixing process; Pr1 and Pr3 are produced by mixing beams and through a linear beam splitter; (b) the double L energy level structure of D1 line in rubidium-85, D and d represent one-photon detuning and two-photon detuning respectively.

和

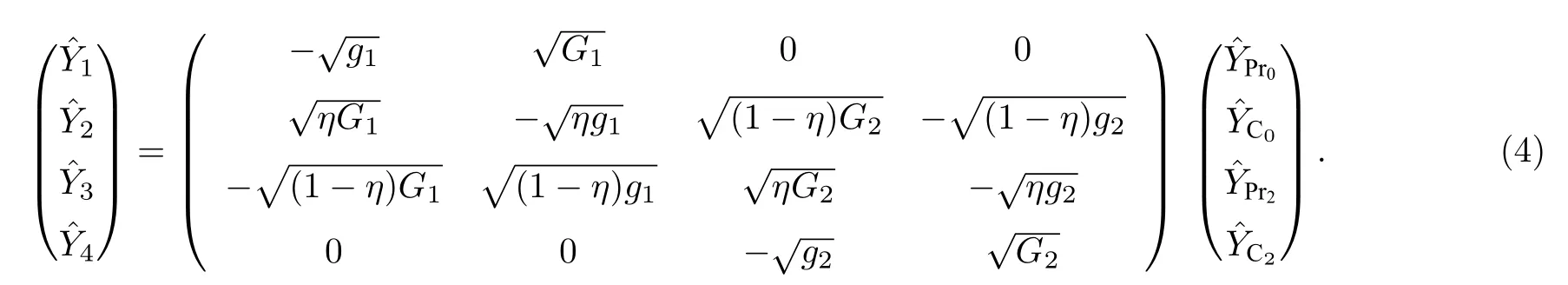
在本方案中, 两个四波混频过程的强度增益G1和G2是相互独立的.在这里分别用

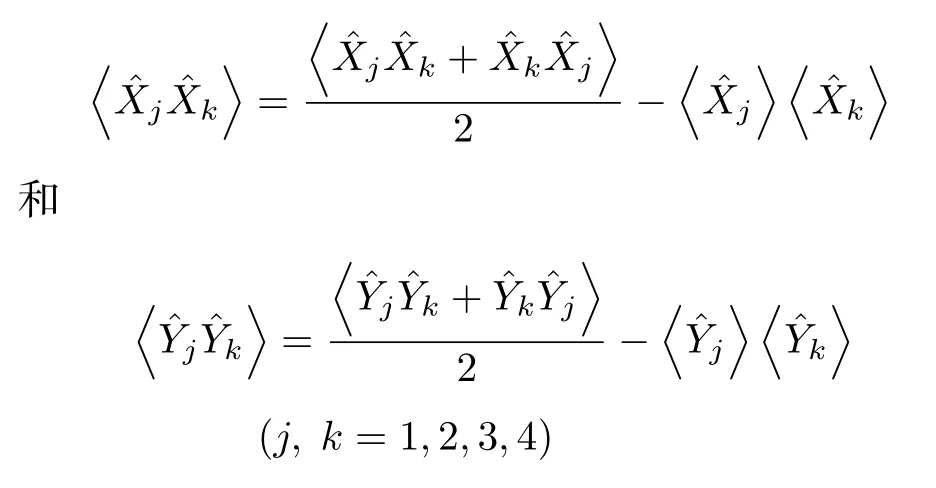
来表示输出场的正交振幅算符和正交相位算符的协方差, 并且在 j = k 情况下时, 其代表的是相应的正交算符的方差.此外, 正交振幅算符和正交相位算符相互正交[3], 即因此,所有光束的协方差如下:

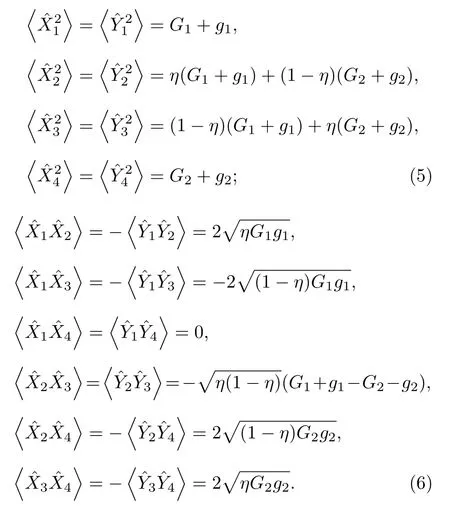
这一节推导了由线性分束器连接的两个独立的四波混频过程的输出场表达式, 接下来将重点研究该系统产生真正的四组份纠缠的可能性以及系统的纠缠结构.

3 系统纠缠结构研究

3.1 四组份纠缠

这一节用部分转置正定判据[34,35]来检验系统的四组份纠缠, 该判据是使用部分转置协方差矩阵s的辛本征值来表示系统的纠缠特性, 如果所有的最小辛本征值v都小于1, 则表示系统是不可分离的.首先研究了这个方案产生四组份纠缠的可能性.在四组份情形中, 需要检验七种可能的两分形式, 其中包括四种 1 × 3 形式和三种 2 × 2 形式, 这七种二分形式如表1所列.

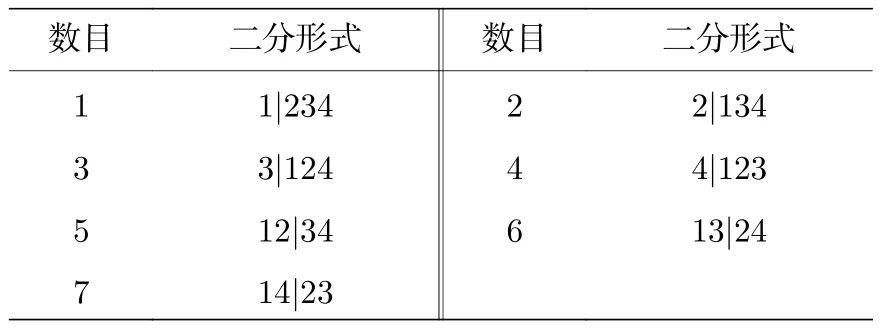
表1 四组份态的七种二分形式Table 1.Seven partitions of quadripartite state.

为了方便, 假设线性分束器的透射率h = 0.5.这里首先研究了四种1 × 3形式, 这种形式描述了每束光是如何与其他三束光纠缠的.图2为四种1 × 3 形式的最小辛本征值 v, 它们都是 G1和G2的函数, 其中图2(a)—(d)分别是部分转置应用于光束 C1, Pr1, Pr3和 C3时的最小辛本征值 v.在图2 中, 对于任何 G1> 1, G2> 1, 最小辛本征值v都小于1, 这表明每束光与剩余的三束光都存在纠缠, 并且纠缠随强度增益G1和G2的增大而增强.此外, 可以看出, 图2(b) 和图2(c) 的最小辛本征值v是相同的, 这是系统的对称性导致的.而当部分转置分别应用于光束C1和C3时, 其最小辛本征值v与另外一个四波混频过程的强度增益无关, 这说明它们的纠缠来源于对应的四波混频过程, 而与另外一个四波混频过程无关.

图2 四种 1 × 3 情形的最小辛本征值 v, 其为强度增益 G1 和 G2 的函数 (a) C1 被部分转置; (b) Pr1 被部分转置; (c) Pr3 被部分转置; (d) C3 被部分转置Fig.2.The smallest symplectic eigenvalue v of all 1 × 3 scenarios, as a function of the power gains G1 and G2: (a) C1 is partially transposed; (b) Pr1 is partially transposed; (c) Pr3 is partially transposed; (d) C3 is partially transposed.

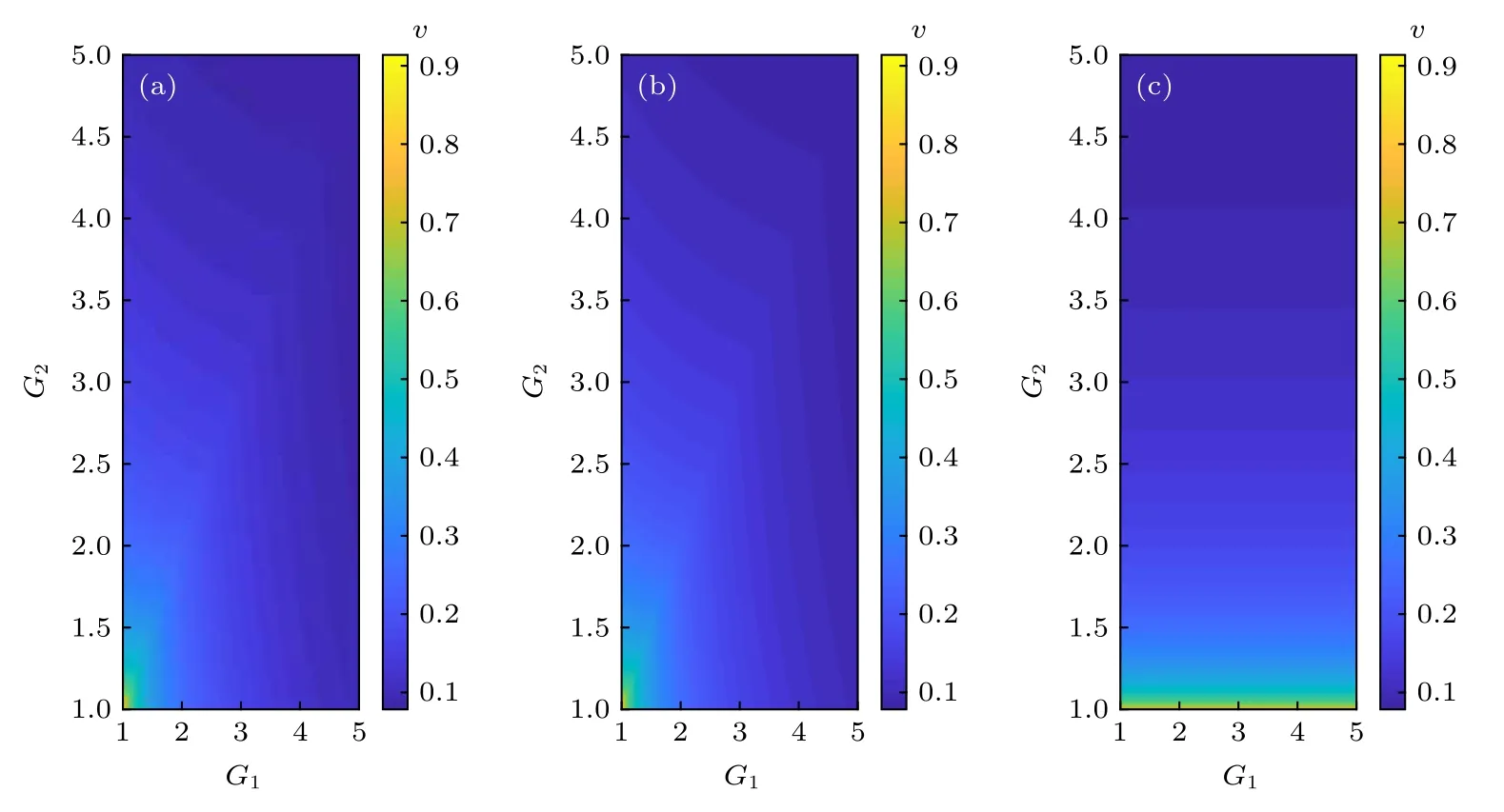
图3 三种 2 × 2 情形的最小辛本征值 v, 其为强度增益 G1 和 G2 的函数 (a) C1 和 Pr1 被部分转置; (b) C1 和 Pr3 被部分转置;(c) C1和 C3被部分转置Fig.3.The smallest symplectic eigenvalues v of all 2 × 2 scenarios, as a function of the power gains G1 and G2: (a) C1 and Pr1 arepartially transposed; (b) C1 and Pr3 are partially transposed; (c) C1 and C3 are partially transposed.

同样地, 也研究了三种 2 × 2 形式, 这种形式是将部分转置应用于四束光中的任意两束光.图3为三种2 × 2形式的最小辛本征值v, 其为强度增益G1和G2的函数, 其中图3(a)—(c)分别是部分转置应用于光束C1和 Pr1, C1和 Pr3以及 C1和C3时的最小辛本征值v.由图3可得, 所有的最小辛本征值v都小于1, 这表明在四组份系统中, 每对光束都与其他光束纠缠, 并且强度增益G1和G2越大, 纠缠越强.值得注意的是, 当部分转置应用于一对光束C1和C3时, 其最小辛本征值v与强度增益G1无关, 并且只受强度增益G2的影响.换句话说, 它们的纠缠来源于第二个四波混频过程,而与第一个四波混频过程无关.

基于上述的分析可知, 在线性分束器的透射率 h = 0.5 以及强度增益 G1> 1, G2> 1 时, 系统所有的最小辛本征值v都小于1, 并且随着强度增益G1和G2增加, 纠缠也在增强, 这表明本文系统可以产生真正的四组份纠缠.

在研究了强度增益G1和G2对四组份纠缠的影响之后, 研究线性分束器的透射率h对四组份纠缠的影响也十分必要.在这里, 为了研究透射率h对四组份纠缠的影响, 假设两个四波混频过程的强度增益 G1= G2= 3.图4 中所有的最小辛本征值v都是透射率h的函数, 其中图4(a)—(g)分别是 部 分 转 置 应 用 于 光 束 C1, Pr1, Pr3, C3以 及C1和 Pr1, C1和 Pr3, C1和 C3时的最小辛本征值v.由图4 可得, 在透射率 h ≠ 0 或 h ≠ 1 时, 系统存在真正的四组份纠缠.此外, 有些最小辛本征值v与透射率h无关, 有些则与其紧密相关.这是因为线性分束器仅连接了两束光, 这会导致部分最小辛本征值v与线性分束器的透射率h相关.

3.2 三组份纠缠

到目前为止, 我们已经证明该方案可以产生真正的四组份纠缠.同时, 研究系统所产生的三组份纠缠和两组份纠缠将有助于进一步了解该系统的纠缠结构.在这里, 假设线性分束器的透射率h =0.5.对于三组份态的纠缠特性, 我们是通过去除系统所产生的四束光中的一束光进行研究的.很明显, 这里有四种可能的三组份态, 并且每种三组份态有三种 1 × 2 形式, 因此, 总共需要检验 12 个1 × 2形式的最小辛本征值v.图5给出了所有三组份态的最小辛本征值v, 其中图5(a)—(c)是由光束C1, Pr1和Pr3组成的三组份态的最小辛本征值 v, 图5(d)—(f)是由光束 C1, Pr1和 C3组成的三组份态的最小辛本征值v, 图5(g)—(i)是由光束C1, Pr3和C3组成的三组份态的最小辛本征值v, 图5(j)—(l)是由光束 Pr1, Pr3和 C3组成的三组份态的最小辛本征值 v.由图5 可得, 在 G1> 1,G2> 1时, 所有三组份态的最小辛本征值 v都小于 1, 并且强度增益 G1和 G2越大, 纠缠越强, 这表明输出场的四束光在去除其中的任意一束光之后仍存在真正的三组份纠缠.此外, 由于系统的对称性, 三组份态 (C1, Pr1, C3)和 (C1, Pr3, C3) 的最小辛本征值v是一样的.而三组份态(C1, Pr1,Pr3)和 (Pr1, Pr3, C3)的最小辛本征值 v 却是不一样的, 其最小辛本征值v分别受到两个独立的四波混频过程的强度增益影响.

图4 线性分束器的透射率 h 对四组份态的最小辛本征值 v 的影响 (a) C1 被部分转置; (b) Pr1 被部分转置; (c) Pr3 被部分转置;(d) C3 被部分转置; (e) C1 和 Pr1 被部分转置; (f) C1 和 Pr3 被部分转置; (g) C1 和 C3 被部分转置Fig.4.Effect of the transmissivity of the linear beam splitter on the quadripartite entanglement of the system: (a) C1 is partially transposed; (b) Pr1 is partially transposed; (c) Pr3 is partially transposed; (d) C3 is partially transposed; (e) C1 and Pr1 are partially transposed; (f) C1 and Pr3 are partially transposed; (g) C1 and C3 are partially transposed.

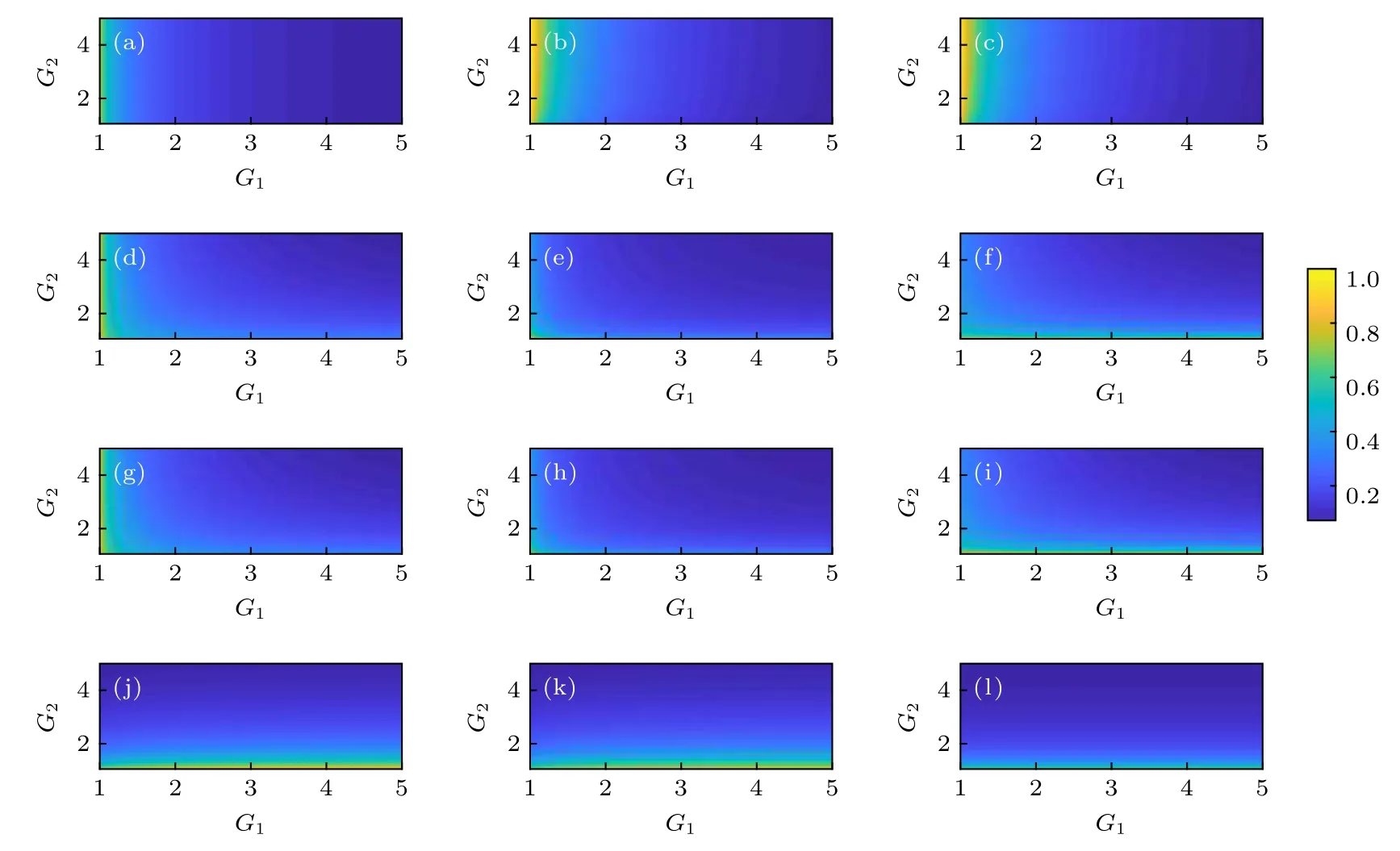
图5 四个三组份态的最小辛本征值v, 其为强度增益G1和G2的函数 (a)−(c)是由C1, Pr1和Pr3组成的三组份态的最小辛本征值v; (d)−(f)是由C1, Pr1和C3组成的三组份态的最小辛本征值v; (g)−(i)是由C1, Pr3和C3组成的三组份态的最小辛本征值v; (j)−(l)是由Pr1, Pr3和C3组成的三组份态的最小辛本征值vFig.5.The smallest symplectic eigenvalues v of all tripartite states as a function of power gains G1 and G2: (a)−(c) The smallest symplectic eigenvalues v of tripartite state composed of C1, Pr1 and Pr3; (d)−(f) the smallest symplectic eigenvalues v of tripartite state composed of C1, Pr1 and C3; (g)−(i) the smallest symplectic eigenvalues v of tripartite state composed of C1, Pr3 and C3;(j)−(l) the smallest symplectic eigenvalues v of tripartite state composed of Pr1, Pr3 and C3.

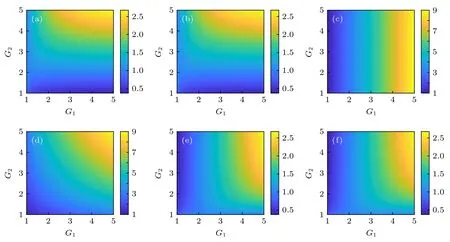
图6 六种两组份态的最小辛本征值v, 其为强度增益G1和G2的函数 (a) 由C1和Pr1组成的两组份态的最小辛本征值v;(b) 由C1和Pr3组成的两组份态的最小辛本征值v; (c) 由C1和C3组成的两组份态的最小辛本征值v; (d) 由Pr1和Pr3组成的两组份态的最小辛本征值v; (e) 由Pr1和C3组成的两组份态的最小辛本征值v; (f) 由Pr3和C3组成的两组份的最小辛本征值vFig.6.The smallest symplectic eigenvalues v of all bipartite states as a function of power gains G1 and G2: (a) The smallest symplectic eigenvalues v of bipartite state composed of C1 and Pr1; (b) the smallest symplectic eigenvalues v of bipartite state composed of C1 and Pr3; (c) the smallest symplectic eigenvalues v of bipartite state composed of C1 and C3; (d) the smallest symplectic eigenvalues v of bipartite state composed of Pr1 and Pr3; (e) the smallest symplectic eigenvalues v of bipartite state composed of Pr1 and C3; (f) the smallest symplectic eigenvalues v of bipartite state composed of Pr3 and C3.

3.3 两组份纠缠

接下来将通过去除系统输出场中的任意两束光来研究剩余两束光的纠缠特性.这里需要检验六种不同的两组份态的纠缠特性.图6为所有的两组份态的最小辛本征值v, 其中图6(a)—(f)分别是由 C1和 Pr1, C1和 Pr3, C1和 C3, Pr1和 Pr3, Pr1和C3以及Pr3和C3组成的两组份态的最小辛本征值v.如图6所示, 有些两组份态(例如由C1和C3组成的两组份态)总不存在纠缠, 这是由于两个四波混频过程是相互独立而导致的.而有些两组份态(例如由C1和Pr1组成的两组份态)的纠缠特性则随着强度增益G1和G2的增大而逐渐减小直至消失, 这是因为随着强度增益G1和G2的增大,线性分束器引入的额外噪声迅速增大, 从而导致纠缠消失.

由于线性分束器的引入, 该系统存在真正的四组份纠缠和三组份纠缠, 并且随着强度增益G1和G2的增大, 纠缠也会逐渐增强.至于系统两组份态的纠缠特性, 有些两组份态总是可分离的.而有些两组份态的纠缠的存在与否却是有条件的, 即它们的纠缠特性受强度增益G1和G2的影响, 随着两个四波混频过程的强度增益G1和G2的增大, 这些两组份纠缠都会逐渐减小直至消失.

4 结 论

本文从理论上提出了一种利用两个独立的四波混频过程和线性分束器产生真正的四组份纠缠的方案, 两个独立的四波混频过程由线性分束器连接.首先应用部分转置正定判据研究了强度增益对四组份纠缠的影响, 结果表明在整个增益区域内都存在四组份纠缠, 并且强度增益越大, 纠缠程度越强, 这表明本文系统能够生成真正的四组份纠缠.然后研究了线性分束器的透射率对系统的四组份纠缠的影响, 发现只要线性分束器的透射率不为0或1, 系统也存在真正的四组份纠缠.最后, 通过研究该系统中可能存在的三组份纠缠和两组份纠缠揭示了系统的纠缠结构.我们的理论研究为实验上利用原子系综四波混频过程产生真正的四组份纠缠提供了一个有效的方案.