量子扩散通道中Wigner算符的演化规律*
2020-05-16张科李兰兰任刚杜建明范洪义
张科 李兰兰 任刚 杜建明 范洪义
1) (淮南师范学院电子工程学院, 淮南 232038)
2) (中国科学技术大学研究生院科学岛分院, 合肥 230031)
众所周知, 量子态的演化可用与其相应的Wigner函数演化来代替.因为量子态的Wigner函数和量子态的密度矩阵一样, 都包含了概率分布和相位等信息, 因此对量子态的Wigner函数进行研究, 可以更加快速有效地获取量子态在演化过程的重要信息.本文从经典扩散方程出发, 利用密度算符的P表示, 导出了量子态密度算符的扩散方程.进一步通过引入量子算符的Weyl编序记号, 给出了其对应的Weyl量子化方案.另外,借助于密度算符的另一相空间表示—Wigner函数, 建立了Wigner算符在扩散通道中演化方程, 并给出了其Wigner算符解的形式.本文推导出了Wigner算符在量子扩散通道中的演化规律, 即演化过程中任意时刻Wigner算符的形式.在此结论的基础上, 讨论了相干态经过量子扩散通道的演化情况.
1 引 言
近来, 量子调控已经成为研究微观世界的一个重要手段, 而用单光子实现量子操控尤为可行, 例如向光腔中逐个注入光子制备非高斯态, 理论上这属于量子扩散机制[1,2].鉴于量子态的Wigner函数包含了量子态的概率分布和相位等信息, 量子态的演化可代之以研究相应的Wigner函数的演化[3−5].本文旨在研究量子相空间的Wigner算符在量子扩散通道的时间演化规律, 它简洁而物理清晰, 展现了从点源函数向时刻高斯型函数的演变, k 是扩散系数, 这里代表 Weyl编序; a†,a是玻色产生和湮灭算符.用有序算符内的积分方法也可进一步将Wigner算符的Weyl编序式转化为其他排序形式, 如正规乘积序等, 为计算量子态的Wigner函数演化规律带来便利.本文安排如下, 先从经典扩散方程推导出量子扩散方程, 并以相干光场为例, 讨论其量子扩散.鉴于初始相干光场的反正规乘积形式是Delta函数, 其演化就体现在从演化为


2 从经典扩散导出量子扩散方程
经典扩散方程是

其中 k 是扩散率, P (z,t) 是系统的某种密度分布函数.下面推导相应的量子扩散方程.我们将密度算符 ρ 用相干态表象中的 P -表示[8,9]:

其中

是相干态, 则密度算符的时间演化满足方程为

将经典扩散方程(1)式代入(4)式即有

利用分部积分法, 并注意到在无穷远处 P (z,t) 消失, 则有

所以

现在利用相干态投影算符的正规乘积表示


则有

将(10)式代入(6)式得到
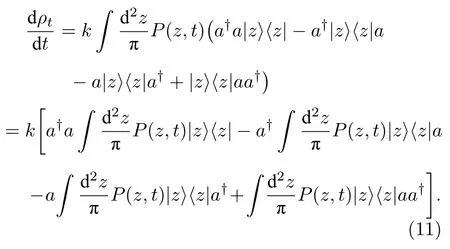
这说明量子扩散方程为

这是从经典扩散方程过渡到量子扩散方程的捷径.
3 相干光场的扩散
当初态是纯相干光场时,

它的正规排序是

利用范洪义等[10]给出的把正规乘积排序变为反正规乘积排序的公式

所以初态是纯相干光场时的反正规乘积排序是
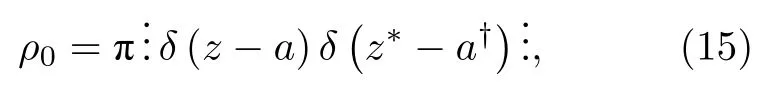
故而它的 P − 表示为

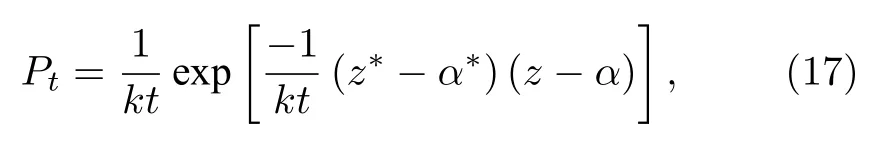
此解满足初始条件, 即:

Pt是密度算符 ρt在相干态表象中的表示, 所以便可得到 ρt的反正规乘积形式为

这就是相干态在扩散通道中的演化公式.再用相干态表象[11]和有序算符内的积分技术[12−14]可以将它化为正规乘积,

通过(20)式可发现它不再是纯态.同时可验证 t rρt=1 , 故而 ρt是一个新光场密度算符, 代表一个广义的混沌光场[15,16].计算 t 时刻的光子数:

4 Wigner算符的 Weyl排序形式
现在讨论Wigner函数在扩散通道中的演化.鉴于 t 时刻的密度算符 ρ (t) 的Wigner函数是[17,18]

这里 ∆ (p,q) 是 Wigner算符, 所以 也可转而讨论Wigner算符在扩散通道中的时间演化, 即从∆(p,q,0)演化为 ∆ (p,q,t).历史上, Wigner算符最早是在坐标表象中定义的[19],

利 用 | q +v/2〉=e−iPv/2|q〉 和 | q 〉〈q|= δ(q−Q) , Q是坐标算符, P 是动量算符, (23)式可化为




与一般算符 H (P,Q) 及其经典对应 h (p,q) 的Weyl对应式为[23]
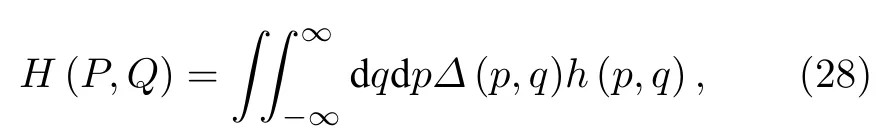
通过比较可见Wigner算符的Weyl排序形式是

从而
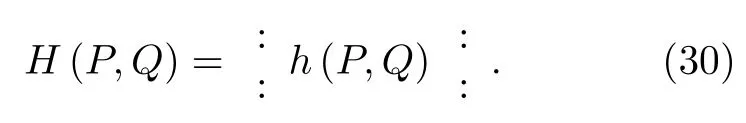
可见 H (P,Q) 的 Weyl排序形式, 可以直接将h(p,q)中的 p →P,q→Q , 并放入内得到.例如,的经典对应是

进一步令

可得Wigner算符的Weyl排序形式是
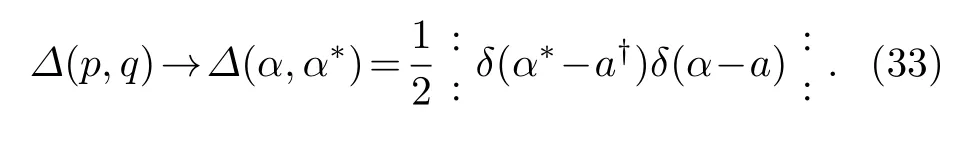
5 扩散通道中Wigner算符的演化方程
由于Wigner算符满足:

Wigner算符本身看作是一个混合态的密度算符,根据(12)式, 它所满足的扩散方程是

此方程也可从Wigner算符的正规乘积形式方程(37)直接导出(具体详见附录A).

对照本文第2节内容可见此扩散方程的经典对应是
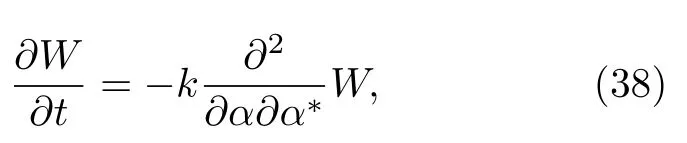
此方程即为Wigner函数 W 应该满足的扩散方程.
6 Wigner算符的演化方程之解
初始的Wigner算符 ∆ (α,α∗,0) 在Weyl编序下是[24−26]

那么类比于本文第2节的结果可知:

其满足的初始条件为

(41)式就是量子扩散通道中Wigner算符的演化律公式, 可以看出, 它简洁明了, 同时展现了从点源函数向高斯型函数的演变, 所以此数学表达式的物理意义十分明晰.
从(40)式可知 ∆ (α,α∗,t) 的经典对应是

根据(28)式可知

而对(24)式做积分可得:

所以 ∆ (α,α∗,t) 的正规乘积是

这样就从(40)式的Weyl编序形式导出了其正规乘积形式.另外, (45)式还可进一步得到验证(具体详见附录B), 即将正规乘积形式转化为Weyl编序形式.举例, 当初态是纯相干态, 那么经过扩散通道后, 从(40)式可知它的Wigner函数为

图1所示为Wigner算符的演化规律, 图1(a)描绘了相干态初始的Wigner函数, 尖峰象征Delta函数; 图1(b) 描绘了 k t=0.8 时高斯型 Wigner函数.对比两图中Wigner函数的峰值及形状, 可以看出相干态在耗散通道的演化情况.

图1 (a) k t=0 , (b) k t=0.8 时, 相干态下 Wigner算符的 演 化 规 律( α =1/2(1+i) )Fig.1.Evolution law of Wigner operator for the coherent state with α =1/2(1+i) for (a) k t=0 ; (b) k t=0.8.
7 结 论
本文引入算符的Weyl编序记号, 导出量子扩散通道中Wigner算符的演化律公式, 它简洁而物理清晰, 展现了从点源函数

向高斯型函数

的演变, k 是扩散系数.由此也可转化为 Wigner算符的其他排序形式, 如正规乘积序.值得指出,对于相干态的演化用了反正规乘积来讨论, 而对Wigner算符的演化用Weyl排序来讨论, 这两者的演化在数学形式上是一样的.
附录A 相空间中Wigner算符所满足的扩散方程
本节验证Wigner算符所满足的扩散方程.由Wigner算符的正规乘积表达式(44)式可算出:

因此有
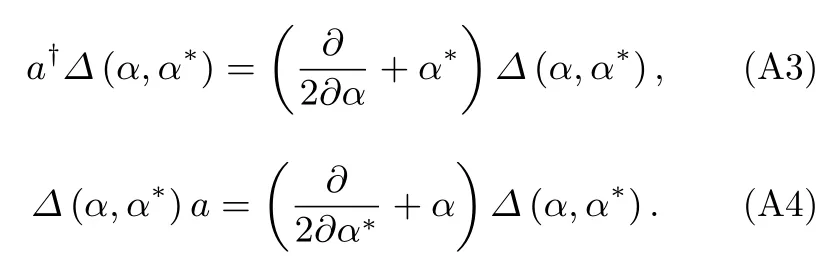
另一方面, 从Wigner算符的反正规乘积表达式

可以推导出:

所以

由以上这些关系式就能导出(36)式.
附录B 化算符为Weyl排序的公式
相干态 | z 〉〈z| 的经典对应是

其Weyl对应式则为

由于是Delta函数型, 所以 | z〉〈z| 的Weyl排序形式为

代入(2)式得到

鉴于

这里 | β〉为相干态, |β〉=exp−|β|2/2+ βa†|0〉, 所以

这就是将算符转化为Weyl编序的形式.当取 ρ 为(45)式时,
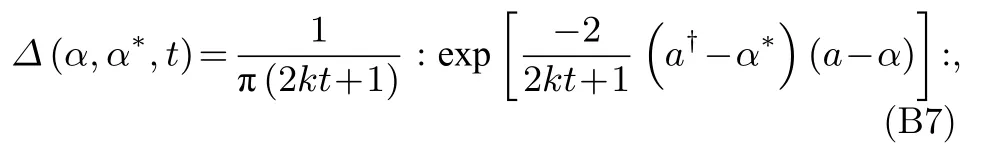
此为正规乘积形式, 则代入(B6)式便可得到Weyl编序形式.

此即验证了(40)式.
