新型冠状病毒肺炎的流行病学参数与模型*

李盈科 赵时 楼一均 高道舟 杨琳 何岱海‡

1) (新疆农业大学数理学院, 乌鲁木齐 830052)

2) (香港中文大学赛马会公共卫生及基层医疗学院, 香港 999077)

3) (香港理工大学应用数学系, 香港 999077)

4) (上海师范大学数学系, 上海 200234)

5) (香港理工大学护理学院, 香港 999077)

一种新型冠状病毒感染导致的肺炎自2019年12月至今在我国以及200多个国家和地区传播.本文旨在介绍近期关于新型冠状病毒肺炎的几个重要流行病学参数的研究进展和估计方法, 包括基本再生数、潜伏期和代间隔, 同时还介绍两个动力学模型及其结果.这些参数刻画了新型冠状病毒肺炎的传播特点, 影响控制策略的制定和有效性.简要来说, 新型冠状病毒肺炎的基本再生数 R0 的中位数为2.6, 潜伏期均值约为5.0 d,代间隔均值约为5.5 d.这表明新型冠状病毒肺炎传播速度快.诸如对确诊病人的隔离治疗、对疑似病例的隔离、对密切接触者的追踪、对疾病信息的宣传和采取自我防护等防控措施能有效降低疾病暴发的风险和规模.

综述

1 引 言

2020年1月30日, 世界卫生组织将新型冠状病毒疫情列为国际关注的突发公共卫生事件(PHEIC).2月8日, 中国国家卫健委将这种肺炎暂命名为“新型冠状病毒肺炎(novel coronavirus pneumonia, NCP)”, 简称“新冠肺炎”.2月11日,世界卫生组织将新型冠状病毒感染的肺炎命名为“ coronavirus disease 2019 (COVID-19)”.3月11日, 世界卫生组织将此次疫情定性为全球大流行(pandemic), 意味着此次疫情的影响范围已远超2003年的非典疫情, 达到全球性传播.这是20世纪以来首次由一种冠状病毒导致的大流行,此前的几次大流行全部是由甲型流感病毒引起的.其中1918-19 A/H1N1流感导致全球约三千万人死亡, 1957-58 A/H2N2 流感和 1968 A/H3N2 流感各导致1百万至4百万人死亡.截至2020年4月10日新冠肺炎已经导致160多万病例和9万多人死亡.在实施有效措施等前提下, 我国的本地疫情已经基本受控, 目前以输入病例为主.防控的成功与对病毒传播特点的了解密不可分.本文旨在介绍描述新冠肺炎传播特点的几个关键参数和建模的一些经验.

武汉金银潭医院的Huang等[1]发表在医学期刊《柳叶刀》上的研究结果给出了受新型冠状病毒感染的41位早期入院治疗病人的流行病学特征.他们指出, 对这种新型冠状病毒的起源、传播途径、人类传播持续时间和疾病临床表现等方面认识尚不够清楚, 需要进一步研究以增进认识.中国疾控中心的Li等[2]发表在《新英格兰医学杂志》和香港大学Joseph等[3]发表在《柳叶刀》上的文章给出了疾病早期传播特征和流行病学重要指标.这三篇文章被后来的研究者广泛引用.

基本再生数 R0(basic reproduction number)是传染病学中最核心的指标之一, 表示一个典型的感染者(一代)在其传染期内, 在一个完全易感的人群中所能感染人数(二代)的期望.通常地, 如果R0>1, 则表明传染病会流行.反之, R0<1 则表明传染病将会逐渐消失.基于传染病传播特征, 建立仓室微分方程模型, 再在无病平衡态处线性化系统得到下一代矩阵, 最后通过计算下一代矩阵的谱半径得到基本再生数[4].实际中, 也可以通过拟合传染病数据(基于确诊日期或发病日期的每日新增病例数据), 得到早期指数增长阶段的增长率(记为r), 再利用增长率和其他参数(如代间隔)来估计基本再生数.根据 R0的定义, 大体有三种估计方法: 第一, 直接从病例调查报告看一个一代病例会导致几个二代病例(假定所有人都易感), 这是一线公卫人员的常用方法.第二, 因为疫情初期感染人数往往指数增长(流行病的特点), 所以用指数函数拟合初期一段时间的病例数据得到增长率r.R0等于代间隔的概率分布(通过分析病例调查报告得到)的矩量生成函数 (moment generating function)在 − r 取值的倒数.第三, 在了解传染病传播的特点后, 写出其传播的动力学模型, 这时 R0等于疾病传播速度乘以病人平均传染期, 通过拟合动力学模型到每日新增病历数据, 从而得到 R0的估计.考虑到防控措施的影响, 有效再生数 Re(effective reproduction number)可以更好地刻画传染病动力学[5],它的计算方法与基本再生数类似.

有证据显示新冠肺炎病人在潜伏期后期有明显的传染性, 所以有必要介绍一下潜伏期的概念.潜伏期常被用作 incubation period和 latent period的中文翻译, 但事实上两者有着显著差异.一般地, incubation period是从个体感染病原体到出现症状的这段时间, 而latent period是从个体感染病原体到具有传染性所经历的时间段(也可以称为潜隐期).换句话说, incubation period 是通过临床上有无症状来刻画的, 但是latent period是通过是否有传染性来刻画的.一般来说, latent period 可以比 incubation period 短, 也可以一样.潜伏期的估算对防疫有重大意义.譬如从最后一个病例连续两次检测为阴性起, 连续观察两个最大潜伏期没有新增病例, 通常看作是本地疫情结束的标志.目前新冠肺炎的疫情数据是基于临床症状统计的, 所以本文所述潜伏期估计主要针对incubation period[6−8].

代间隔 (generation interval, GI)指一代病例被感染的时间到二代病例被感染的时间之间隔.代间隔对于衡量疾病的传播速度具有重要作用[9,10].因为通常不知道病人被感染的时间, 所以代间隔不可观测.而有症状的病人发病时间(首次出现症状)通常是可知的.所以通常用相邻两代病例出现症状的时间差来近似, 也称为代间隔(serial interval,SI).实际上这两者有差别, 然而因为前者通常不易观测, 所以在实践中常以后者来代替.关于新冠肺炎, 有些文献发现代间隔接近或者短于潜伏期, 由此推断染病者在潜伏期后期即具有传染性[11].有工作发现43%的传染是发生在症状出现前[12].

2 基本再生数公式与重要参数统计

Wallinga和Lipsitch[9]从种群增长的角度由Lotka-Euler公式导出的基本再生数 R0的计算公式为

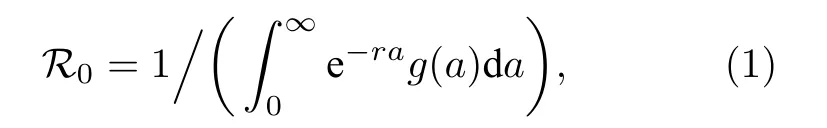
由常微分方程刻画的传染病动力学模型, 以van den Driessche 和 Watmough[4]提出的计算基本再生数 R0的方法被普遍使用.在此基础上, 基本再生数 R0的计算方法推广到年龄结构模型、周期微分方程模型、反应扩散方程模型以及时滞微分方程模型等.

表1 不同模型或分布下的基本再生数 R0 的计算公式Table 1.The formula of the basic reproduction number R0 under different models or distributions.

增长率r也可通过其他方法得到.在这次疫情中, 国内外的多个团队利用在海外确诊的病例数、病例从暴露到被检测到的时间、以及向海外人员输出流量估计出武汉市在不同时间的可能感染人口规模和基本再生数[13−15].我们在 PubMed, bio-Rxiv, medRxiv 和 Google Scholar等数据库及预印本平台分别按关键词“basic reproduction number& 2019-nCoV (COVID-19, NCP)” , “ incubation period (latent period) & 2019-nCoV (COVID-19,NCP)”, “serial interval & 2019-nCoV (COVID-19, NCP)” 进行搜索, 时间段是 2019年11月1日至2020年2月10日左右, 筛选获取的关于前述3个参数的信息汇总见表2—表4[1,2,3,5−7,11,16−25].

厘清关键参数的定义和最新估值是非常重要的.比如在疫情初期Li等[2]根据6例病人得到代间隔 7.5 d.因为病例数少, 估计的可靠性偏弱.后期的大样本统计发现7.5 d可能高估了.但是相当多的建模仍然继续使用初期估计.而且有发现代间隔SI为负的情况(一代病例出现症状的时间晚于二代病例出现症状的时间), 但是要注意, 根据定义, 真正的代间隔GI是不可能为负的(一代病例被感染的时间必然早于二代病例被感染的时间).只有在充分了解定义后, 才能明白此时那些负的观测是不能用于估计GI的分布的.只有理解潜伏期(以症状论)与潜隐期(以传染性论)的差别, 才能写出简洁合理的动力学模型.所以, 对传染病基本参数的理解和估计是极其重要的.

表2 新冠肺炎基本再生数总结Table 2.Summary of the basic reproduction number R0 for COVID-19.

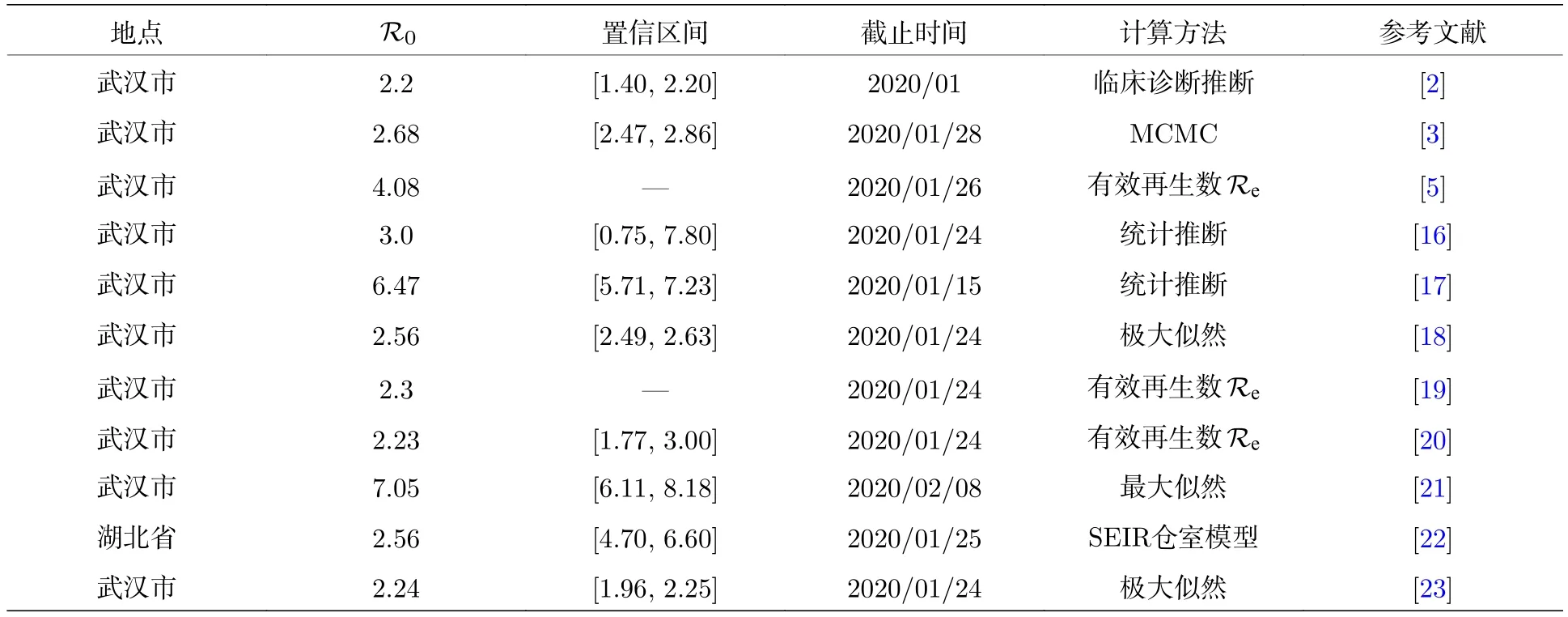
表2 新冠肺炎基本再生数总结Table 2.Summary of the basic reproduction number R0 for COVID-19.

注: 表2—表4中参考文献数据均来自国家卫健委、湖北卫健委、中国CDC等网站及已发表文献.

?

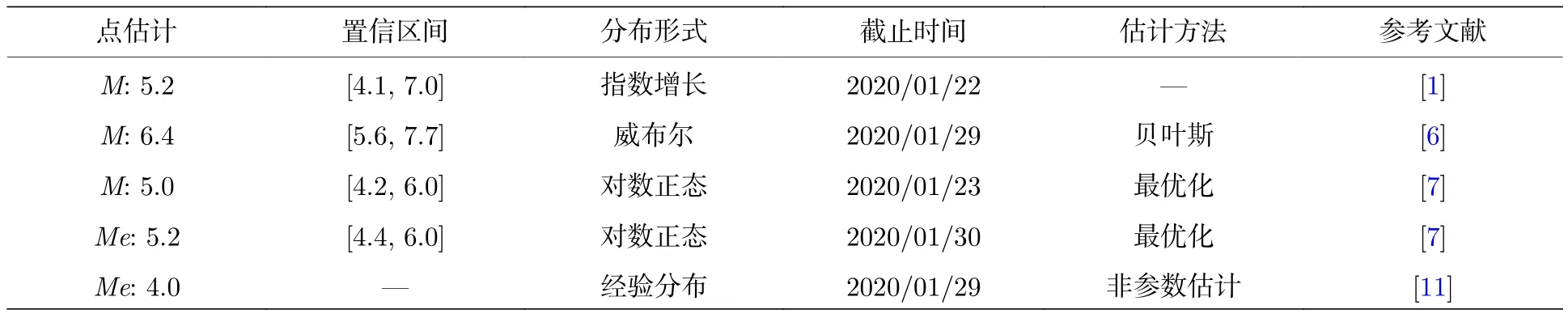
表3 新冠肺炎潜伏期统计Table 3.Summary of the incubation period for COVID-19.

表4 新冠肺炎的代间隔统计Table 4.Summary of the serial interval for COVID-19.

3 动力学模型

经过两个多月的努力, 武汉市的新冠肺炎疫情得到了全面有效的控制, 终于在2020年4月8日迎来解封.但是对武汉市的新冠肺炎疫情的研究在一段时间内仍然是重要的.比如1918年流感一直被研究, 已经有一百多年了.针对武汉市的新冠肺炎疫情, 根据疫情的发展阶段、研究动机以及模型呈现形式, 目前已经有不少出色的建模研究.下面简要介绍本课题组所做的部分工作, 分别称之为概念模型(conceptual model)和模拟动力学模型(imitation dynamics model).

3.1 概念模型

3.1.1 模型及其参数

团队成员此前对1918年流感在英国伦敦的三波疫情的研究于2013年发表在英国皇家学会的通讯上[26], 受到媒体广泛关注, 被认为首次揭示了这一现象背后的机理.此次新冠肺炎轻微症状患者的比例高和代间隔相对短的特征与非典(SARS)和中东呼吸综合征(MERS)相差较大, 而与1918年流感在伦敦流行的特点有相似之处, 体现在具有相近的基本再生数与粗感染死亡率(raw infection fatality rate).有临床工作发现两种病毒从病人呼吸道排出的时间规律也相似.同时注意到, 此次疫情发展过程中政府的控制措施和民众的反应, 诸如封锁城市、延长假期、隔离患者和入院治疗等措施都影响新冠肺炎的流行趋势.综合这些因素, 根据仓室建模的思想, 提出了以下概念模型[27]:

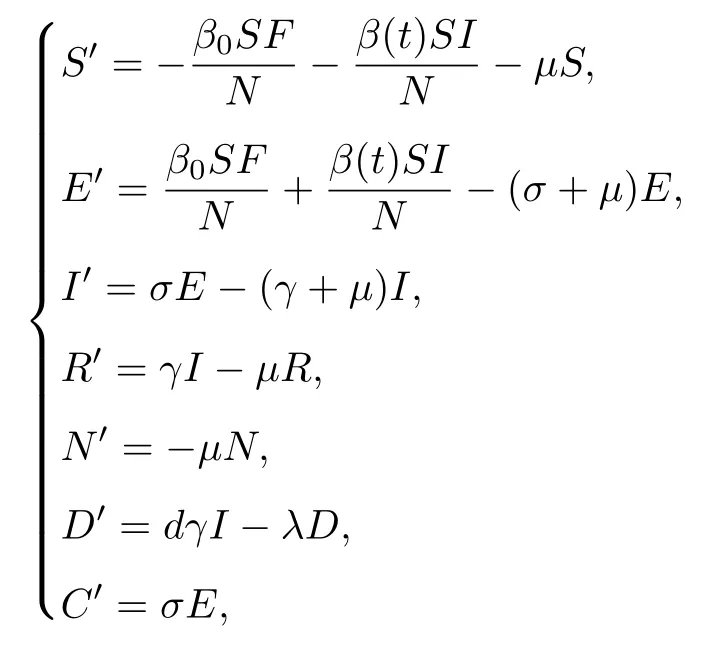
其中β(t)= β0(1− α)(1−D/N)κ.

模型基于经典的 SEIR (易感-暴露-染病-移出)模型, 这里环境传染源F (来自动物的病毒),总人口数N, 对危重和死亡病例的重视人数D, 累积病例数C (包含报告和漏报)的耦合.模型基于以下3条假设: 1) 2019年12月前疾病的传播方式是动物感染人(由F刻画), 这之后主要是人传人(由 β (t) 刻画); 2) 政府的阶段性控制措施效力主要发生在 2020年1月23日之后, 由 β (t) 中 α 刻画,如2020年1月23日—29日期间 α =0.4249 , 在这之后 α =0.8478.β (t) 中 κ 主要用来刻画民众对疫情的响应强度; 3) 武汉市居民出城主要集中在2019年12月31日至 2020年1月22日之间.病例数据主要来自官方公开数据和公开发表文献数据, 模拟过程中也考虑了报告数据的不完整性和滞后性等因素.模型中的一部分参数由合理假设给出, 如儿童病例较少, 可假设易感人群占总人口比例为90%, 其他参数由病例数据拟合而得, 详见概念模型[27]中表1.

此模型强调了公众采取自我保护措施的重要性, 这一非药物手段的作用已被许多国内外研究者所认可, 也符合逻辑.同时在模拟过程中考虑确诊率和确诊延迟也非常重要, 但仍有相当多的工作忽视它.确诊率在1月3日以前可能只有2%, 因为人们对于这种新病毒认知有限, 而不可避免地出现错漏.但是随着人们对病毒认识的增加和检测能力的改善, 到封城前确诊率已达 14%.事实上, 早期武汉市的新冠肺炎病人采样需要送北京检测, 后来才可以在武汉本地检测.检测能力从开始的每天200例, 到2月5日增长到每天上万例.只有快速检测确诊, 病人才能及时收治, 疫情才可能得到控制.我们关注的是能否通过模型模拟确认检测能力的变化.在不清楚检测能力的情况下, 认为不能简单地追求拟合的好坏.错误的假设(比如认为检测能力是恒定的)往往得出错误的结论.概念模型的新颖之处包括: 考虑了公众自我保护行为的效果,考虑了确诊延迟(即模型的结果在早期要后推两周才能与报告新增病例对比), 考虑了确诊率的变化(没有直接拟合, 而且通过对比模型结果与报告新增反推检测率的变化), 使用了较合理的潜隐期(从而考虑了潜伏期末期的传染性), 考虑了封城前人口的移出, 考虑了12月前环境到人的传播等.

3.1.2 概念模型结果

排除政府举措强度和公众响应强度一方或者双方不发挥作用的两种极端情形.考虑两种强度均存在的情形, 主要模拟结果如下 (这与其他研究团队的研究结果基本一致).

(I) 相对于最初动物感染的41例病例, 我们预测有145例, 得到确诊的报告率约为28%.

(II) 截止2020年1月18日, 武汉市的累积病例为4648人.

(III) 相对于香港大学专业团队估计的2020年1月27日的累积病例数 25630 (95% CI: 12260—44440), 我们预测为16589例, 估计值处于此置信区间内.

(IV) 武汉市的累积病例在2020年4月底将会达到84116例(其中包含无症状和未登记的).

(V)在 2月17日后, 基本再生数 R0降为 0.疫情的确诊率随时间的仿真结果见图1.

图1(a)展示了概念模型结果与实际报告病例的比对.注意概念模型关注的是整体上的符合, 并不是完美的拟合, 而图1(b)展示了确诊率的变化.这个模拟的确诊率的变化是政府强有力控制措施的一个体现.只有确诊率达到一定程度, 武汉市的疫情才能在相对短的时间内得到控制.早期的快速扩散正是由于确诊能力不足导致的.有没有考虑确诊率的变化严重影响模型的拟合和对结果的解释.当一种新的传染病出现时, 开始人们对疾病的病原学和流行病学认识有限, 导致确诊率不高, 随着对传染病的逐步了解, 检测试剂盒的研发与投放, 检测能力逐步提升.这些情况在建模和拟合数据时都应该考虑, 否则得到的结论很可能与实际情况产生较大偏差.

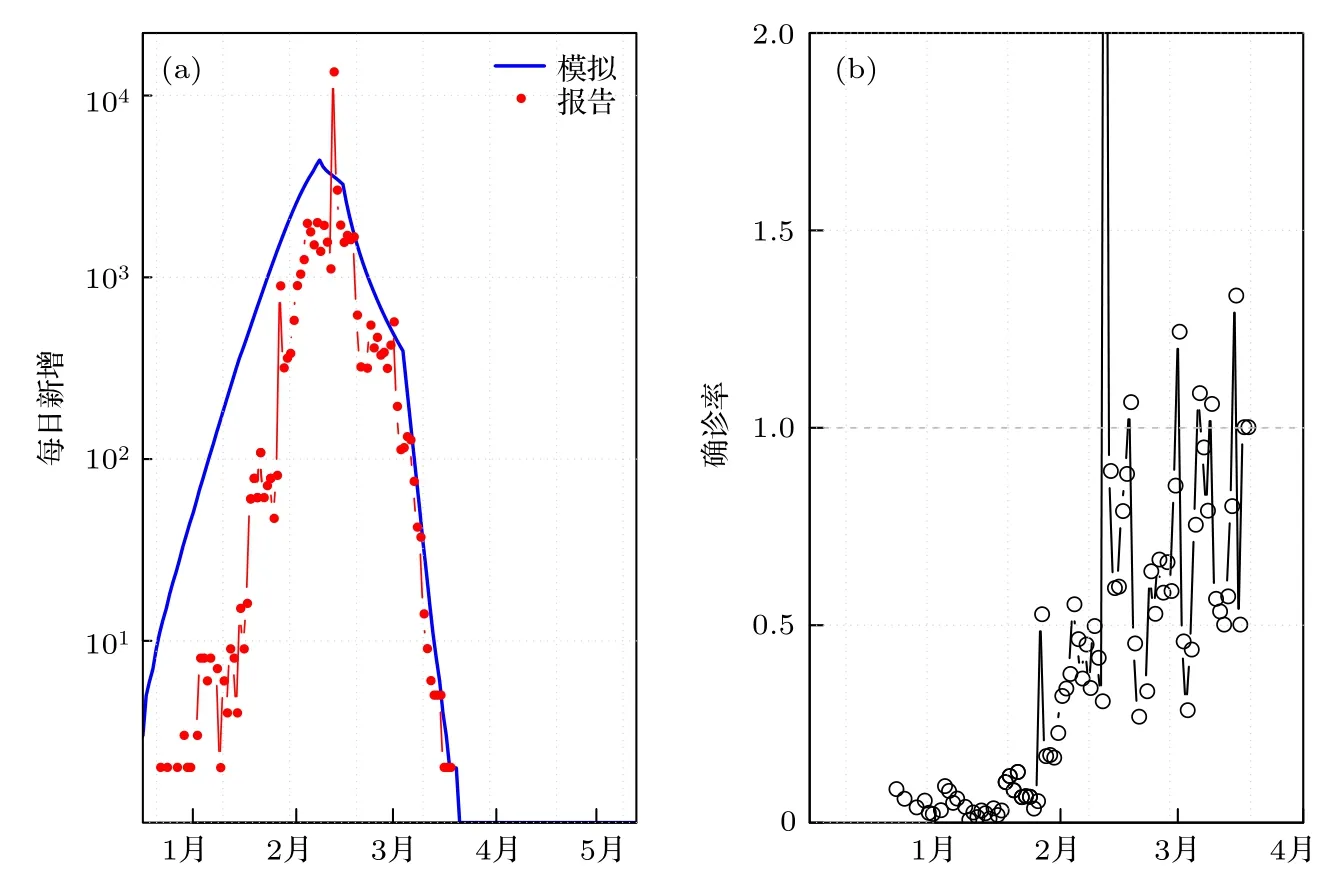
图1 (a)每日新增病例模拟与确诊报告对比; (b) 每日确诊报告率Fig.1.(a) Daily new cases simulated versus reporting; (b) daily reporting rate.

3.2 模拟动力学模型

在模拟动力学模型[28]中我们进一步考虑了公众的行为改变.实际上是用不同的建模思想再次强调公众的行为改变(我们假定是自主的, 实际上有部分是政府引导)的重要性.这里仍以武汉市为例.我们强调模型应该考虑公众的行为改变, 这样得到的预测结果(比如疫情规模)才能比较合理.不能简单地套用经典的传染病模型.因为经典的传染病模型给出的疫情规模往往是高估的, 疫情规模(在一次暴发中被感染人口占总人口的比例, 假定初始所有人易感)记为 z, 则 z =1−exp(−R0z) 给出 z与 R0的关系[29].这个关系再次突出了 R0的重要性.在1918年流感和2009年流感中, 一年后感染率都远低于理论上的预测, 其中一个重要原因是理论预测忽视了公众行为的改变对疫情发展的影响.

3.2.1 模型及其参数

根据人们采取的防护措施(如戴口罩、勤洗手、减少聚集性活动等)的意愿和防护效果的不同,我们在传统的SEIR模型的基础上, 将易感人群分成采取防护措施者M和没有采取防护措施者U两部分.此时总人口 N =U+M+E+I+R.另外加入参数p用来描述人们愿意采取防护措施的概率.疫情的有效控制在很大程度上也取决于民众采取防护措施意愿的大小, 模型如下[28]:

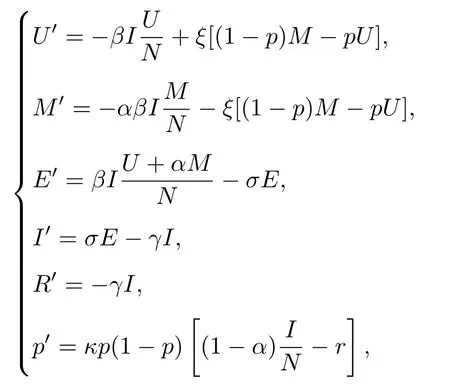
这里 β 是传播系数, α 表示采取防护后传染系数减少的幅度, ξ 表示对采取防护措施与否态度的转变量, κ 为态度转变后的得失的敏感系数.

3.2.2 模型结果

选择欧拉固定步长多项式分布(Euler fix-step multinomial distribution)来模拟自然系统的噪声,选取泊松分布作为似然函数来模拟观察噪声和拟合数据, 并且以此选取置信区间的评判准则以及初值等.同时也将估计的参数值和模型输出结果(如病例数等)和文献中的发现做对比, 来检验我们的分析结果.通过调整得失系数 κ 和措施有效性系数α来模拟它们对武汉市的新冠肺炎疫情高峰、规模等的影响.主要结果为:

(I) 武汉市的新冠肺炎的基本再生数 R0= 2.5(95% CI: 2.4—2.7);

(II) 高峰时期 1000 人中大约有 0.28 (95% CI:0.24—0.32)个染病者, 人群中最终大约有1.35%(95% CI: 1.00%—2.12%)的染病者;

(III) 疫情大体在 2月9日 (95% CI: 01/31/2020—03/27/2020)得到了遏制(此时有效再生数Re<1);

(IV) 民众提高认知(增加 κ )和加强阻断传播(减少 α )可以有效控制新冠病毒的传播.

这里只简要介绍建模思想、模型方程和主要结果.我们认为经典模型一般不适用于疫情最终规模的预测, 应该考虑公众行为的改变(有部分是政府措施导致).确诊率随时间的变化也应该在对比模型结果与实际报告数据时加以考虑, 才有可能得出较合理的疫情发展趋势和规模预测.规模的预测是相当困难的课题, 通常需要血清学研究来证实.

4 全球疫情趋势

在厘清概念的基础上, 有很多现成的程序包可以使用.比如EpiEstim R程序包就是基于(1)式的R程序包.我们研究中除使用这个程序包外, 同时结合一个数据包nCoV2019, 它提供的实时各国每日新增确诊数据, 总确诊数前40位的国家的疫情显示在图2和图3中.这里的粉红色曲线代表瞬时再生数, 就是在一个时间窗口内使用(1)式.当瞬时再生数高于1时, 每日新增会快速增长.当瞬时再生数低于1时, 每日新增会逐渐下降.瞬时再生数通过1对应的时间为拐点.随着各国局部出现一定程度的群体免疫(感染人口增加、易感人口下降)及社交距离扩大, 一部分国家已经出现拐点.同时, 仍然有一部分国家处于上升阶段.由图2和图3可知, 再生数曲线(红线)在绿线以下, 即当时的瞬时再生数小于1, 表明此时疫情得到控制.在3月30日之后, 奥地利、意大利、澳大利亚和挪威等国家疫情基本得到控制.而巴西、印度、日本和塞尔维亚疫情形势依然严峻.中国自3月份以来,尽管再生数在一段时间有大于1的情况, 但这段时间主要是输入病例, 与以本地病例为主的其他国家不同.总的来说, 进入 4月份, 全球疫情出现放缓趋势, 但巴基斯坦、秘鲁和法国等国也出现了反弹,各国家仍需警惕.中国控制新冠肺炎的经验值得其他国家借鉴.

5 结论与讨论

我们的统计分析表明, 在疫情初期, 基本再生数 R0的均值为 3.4, 中位数为 2.6, 潜伏期均值约为 5.0 d, 世代间隔均值为 5.5 d.利用 van den Driessche和Watmough[4]提出的下一代矩阵的方法, 在疫情暴发初期由概念模型得到的基本再生数R0=2.8, 但整个疫情过程中有效再生数 Re随时间在变化.新冠肺炎的病死率与1918年大流感的病死率2%大体一致.

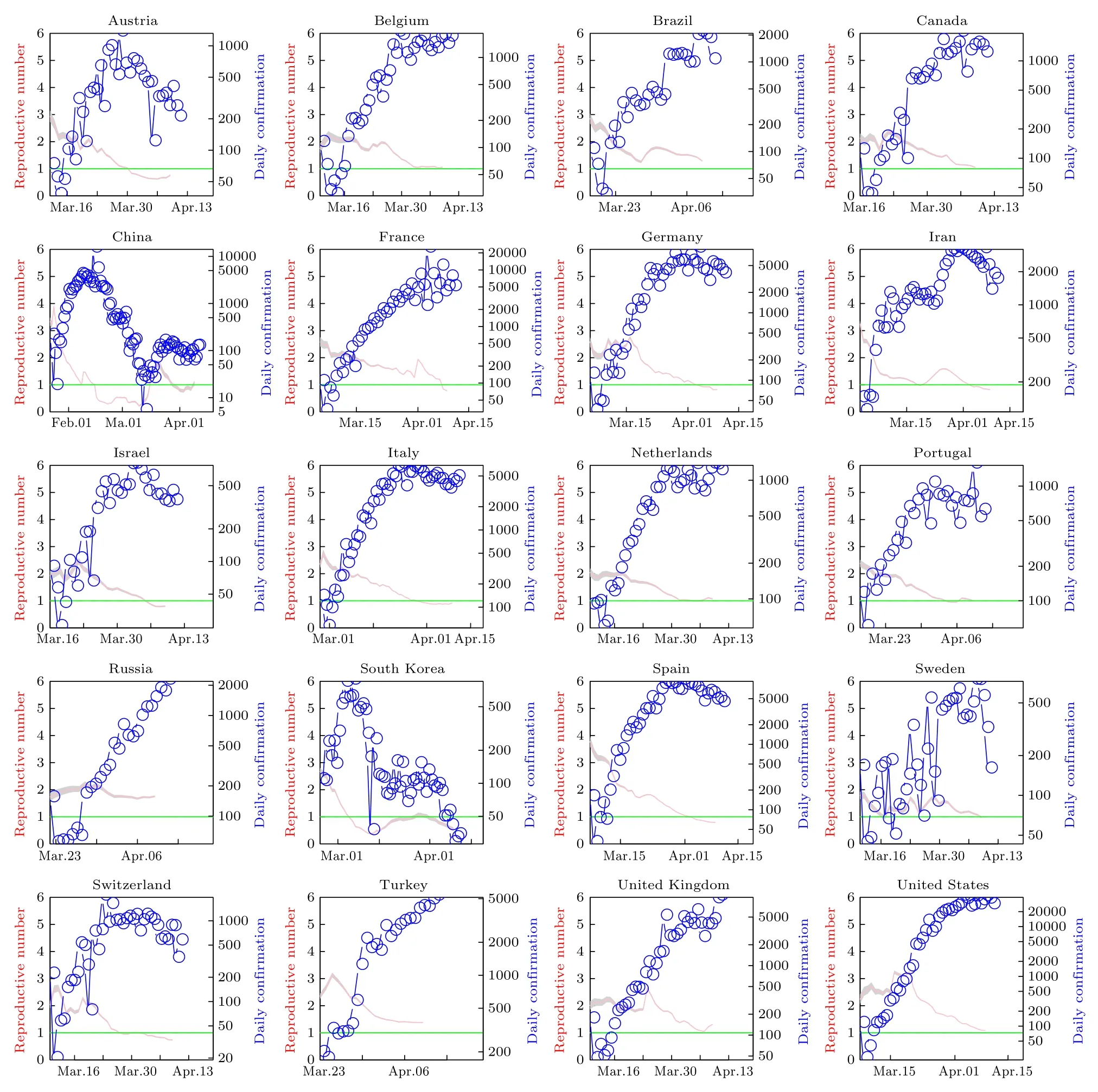
图2 累积病例最多的前20个国家的日确诊病例和瞬时再生数的曲线关系图Fig.2.Curves of daily confirmed cases and instantaneous reproductive number of the top 20 countries with the most cumulative cases.

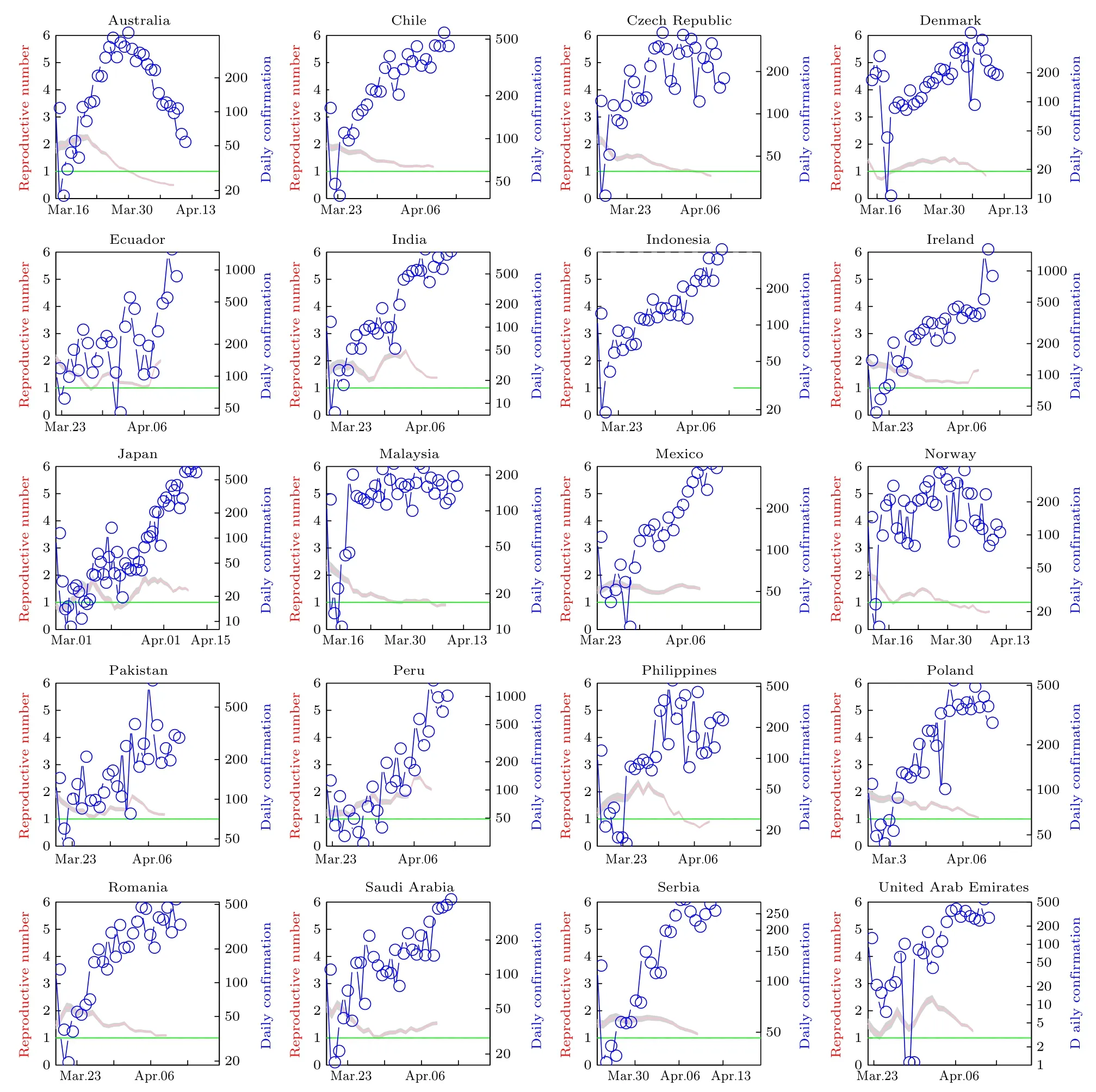
图3 累积病例最多的第21—40国家的日确诊病例和瞬时再生数的曲线图Fig.3.Curves of daily confirmed cases and instantaneous reproductive number of the 21st − 40th countries with the most cumulative cases.

对基本再生数 R0、代间隔(SI)和潜伏期的估计的准确性一方面受到所建立的数学模型及其假设的影响, 另一方面也取决于收集到的数据数量和质量、数据的分布形式的假设、数据的完整性和纯粹性等因素.Guan等[11]对早期1099例入院患者进行的研究表明潜伏期的中位数可能较短, 为4 d.除了基本再生数、潜伏期和代间隔, 倍增时间(doubling time, 感染人口规模加倍所花费的时间)也是研究传播力的重要参数[2,3].医学及健康大数据分析和建模在此次疫情的防控过程中得到体现[30,31].有团队利用腾讯或百度平台得到人口在城市间的流动数据, 还有团队利用了手机数据[32].

疫情暴发早期, 新增病例以指数增长, 这个指数体现了基本再生数和代间隔的概率分布的关系.随时间变化的新增病例、基本再生数和代间隔的概率分布这3个量, 理论上知道其中两个可以求出第3个.通常是根据新增病例的时间序列、代间隔的概率分布求出基本再生数(在疫情初期成立).随着疫情的发展, 也可以根据新增病例的时间序列和代间隔的概率分布, 求出瞬时再生数.以3月9日至4月6日期间公开的数据为基础, 我们绘制出了目前累积病例全球前40位的国家的再生数随时间的变化图(见图2和图3).

疫情能否得到控制取决于把有效再生数降到1以下.通过疫情数据, 结合报告率(reporting rate)可以拟合推断出病例的增长速度, 再结合代间隔的分布, 就可以准确地估计基本(有效)再生数.防疫措施能降低有效再生数, 通过 Re=1 决定所需要采取的措施的强度.假设研发出安全便宜的疫苗, 且有效性为 100%, 根据 Re=ρR0, 其中 ρ 为易感人群占总人口的比例, 临界接种率为 1 −1/R0.即当疫苗接种率大于这个临界值时, 有效再生数Re将小于1, 传染病将逐渐灭绝.通过防疫措施,如对确诊病例的及时隔离和治疗、对疑似病例和密切接触者进行隔离和检查、提高个人的防疫意识,能在一定程度上降低有效再生数.利用优化方法可以更加合理地统筹调配各种防疫资源, 最大程度地降低有效再生数.此外防疫目标也需要考虑其他的重要指标, 如病死率 (case fatality rate, 在流行病学中指一定时期内因患某种疾病的死亡人数占总患者的比率)和倍增时间等[33], 这些都是新冠肺炎防疫的重大课题.

基于流行病学的大数据分析和统计建模, 在疫情暴发早期及时对传染病的传播速度、模式和流行规模作出准确估算, 对防控政策及时地进行评估,这些都对早期疫情控制起到了重要作用.随着疫情的发展, 政府也实施了一些强有力的防控措施, 我们相信大数据分析和数学建模将会继续在后续的防控措施效力评估和疫情预测中发挥重要作用.