利用比较揭示概念本质

朱莉萍

[摘要]数学概念是构建数学认知结构的重要基础。在数学概念教学中，比较是行之有效的教学方法，它能帮助学生通过比较找出事物的本质特征和非本质特征，并在此基础上加以概括，从而掌握概念的本质属性。

[关键词]概念;比较;比例;放大与缩小

[中图分类号]

G623.5

[文献标识码]A

[文章编号] 1007-9068（ 2020）11-0020-02

【案例背景】

数学概念是进行判断、推理、构建数学认知结构的重要基础，是发展学生智力和培养学生数学能力的前提，是数学教学的重要内容。

很多教师虽然也重视数学概念的教学，但是过分偏重定义的叙述，强调识记概念内容，忽略对概念形成过程的探究，加上利用大量练习代替探究，导致学生理解不透概念、辨别不清相似概念。由于没有经历概念形成的过程，学生的抽象、概括、归纳等思维能力也无法得到发展及提高。

比较是人脑把各种感性材料加以辨析，确定它们的异同及彼此间相互关系的思维过程。比较是以分析为前提，从一般到特殊的归纳方法。在数学概念教学中，比较是行之有效的教学方法。合理、巧妙地运用比较，可以帮助学生找出事物的本质特征和非本质特征，掌握概念的本质属性。下面以“按比例放大与缩小”的教学为例进行论述。

【教学片段】

出示：

师：看，老师带来了什么？

师：这么可爱的小猴，我把它变大一些。

出示：

师：同样是变大，有什么不同？与同桌交流你观察的结果。

生1：一幅图中的小猴变长了，另一幅图中的小猴变扁了，还有一幅图中的小猴不长不扁，但是变大了！

生2：变大的小猴形状没有变。

生3：变长和变扁的小猴虽然变大了，但是形状也变了。

师：像这样不改变形状的放大，数学上就叫作图形的放大。为什么变大后，形状变了，而放大后形状不变呢？（教师将4幅图放在方格图中，学生观察分析、思考交流）

生4：图2-3跟图1相比，长没有变，宽扩大了;图2-1宽没有变，长扩大了，所以才会变形。

生5：我发现图2-1的长扩大了2倍，宽也扩大了2倍。

生6：图2-1的长和宽同时扩大2倍，所以形状不变。

师：算一算，图2-1与原图形对应，边的长度比是多少？

生7：2：1。

师：我们可以说图2-1是把原图形按2：1的比放大的。

出示：

师：从大三角形到小三角形，是图形的缩小吗？

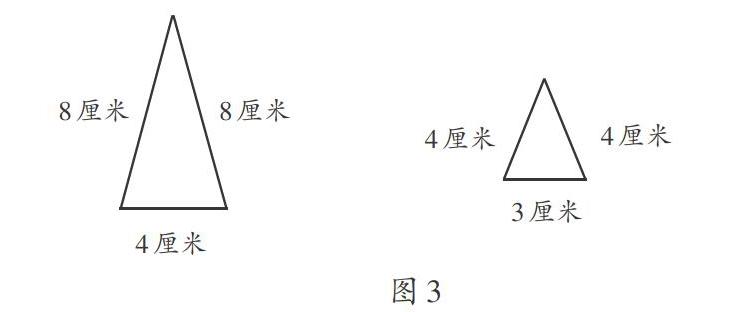
生。：不是，因为两条腰是按1：2缩小的，而底边是按3：4缩小的。

生9：每条边缩小的比应该一样，要么都按1：2缩小，要么都按3：4缩小。

师：也就是说三条边缩小的比例不同。

师：如果把大三角形按1：2的比缩小，那么缩小后的三角形的每条边长是多少厘米？

生10：两条腰的长度还是4厘米，底边应变成2厘米。

师：怎么算出底边是2厘米的？

生11：大三角形的底边是4厘米，按1：2缩小，就是4÷2=2。

師：把大三角形按3：4的比缩小，那么缩小后三角形的每条边长应是多少厘米？

生12：底边是3厘米，腰是6厘米。

师：左下角的小图是大图缩小后得到的吗？是按几比几的比缩小的？

生13：是按1：9的比缩小的。

生14：不对！应该是按1：3的比缩小的。

师：现在出现两个结果，到底是1：9，还是1：3？

生15（边说边比画）：小图的面积占大图的九分之一，所以是1：9。

生16：虽然小图的面积占大图的九分之一，但是按几比几的比缩小应该看对应边的比，缩小后的图形与原来的图形对应边的比是1：3，所以是按1：3缩小的。

师：想一想，判断一个图形是按几比几放大或缩小，应该看什么？

生17：应该看放大前后或缩小前后对应边长的比。

师：1：9是它们的什么比？

生18：面积比。

【案例反思】

一、利用比较，明确概念内涵

概念形成是一个由具体到抽象的过程。概念的学习是从感知大量的学习素材开始的，通过对学习素材的观察分析，在头脑中建立起学习对象的正确表象后，才能引入概念的意义。小学数学概念的描述普遍比较抽象，学生学习理解概念存在一定难度。对于概念教学，教师先要分析这个概念是建立在学生哪些已学的数学知识或学生已有的生活经验基础上，继而思考如何利用引申、点拨、比较等方法沟通新旧知识间的联系，巧妙地引出新概念。

六年级的学生在生活中都有过“图形变大”的直观感受，但要从生活中“图形变大”的感性认识上升到对数学中“图形放大”意义的理解，需要经历一个去粗取精的过程。教师在原图的基础上出示了三幅变大后的图，即长不变宽变、宽不变长变、长宽都按一定的比例变大的三幅图。因为对比夸张、特征明显，学生很快在三幅图中找出图2-1虽然变大了但没有变形。夸张的对比，直观凸显了“放大”的数学本质，使学生明确感受到图形变大有变形和不变形之分。在学生直观比较后，教师再揭示“不改变图形形状的变大，在数学上就称为图形的放大”，学生对图形放大的体会就更深刻。这次比较由生活意义上的“变大”自然过渡到数学上的“放大”，接着借助小方格让学生再观察，学生在比较中得出图形的长和宽得同时按照相同的比例变大才行，从而发现数学上“图形放大”与一般的“图形变大”的本质不同，更深刻地理解了图形放大的数学意义。至此，直观的感性认识升华为对概念本质的理性认识，从而顺利扩展和丰富原有认知结构。

知识迁移是指先前学习的知识对以后学习的知识所产生的影响和作用。在学生已经掌握了图形放大的数学意义之后，图形按比例缩小已经呼之欲出。教师自然地利用了知识的迁移进行教学，没再出示方格中的图形，而是直接呈现标有边长的两个等腰三角形，让学生判断“是大三角形到小三角形的缩小吗？”。比较的过程就是学生利用图形放大含义进行逆思考的自主迁移过程，是学生尝试运用图形缩小的意义自主进行探究、构建知识的过程，至此，学生初步学会怎样按一定比例计算图形缩小后各边的长度。这次比较是建立在学生认知的实际状态之上，利用并促成了知识的自主迁移，自然而然引出后序学习“如何根据一定的比画出已知图形放大或缩小后的图形”。

二、利用比较，区分易混淆的概念

有些数学概念、公式，表面上看非常相似，本质上却有很大差异，若不仔细观察，认真比较辨析，学生常常会混淆。因此教学时，教师要引导学生多角度、多方位进行思考、比较，帮助学生准确地抓住概念的本质属性、排除概念的无关特征。

例如，按一定比例将图形放大或缩小，指的是放大或缩小前后图形对应边的比，但是图形在放大或缩小时，除了边长的变化外，面积的变化也非常明显，因此学生很容易把图形按对应边的比缩小误以为是按图形面积的比缩小。把缩小的图叠放在原图左下角的图3-下引发了学生新的认知冲突：究竟是按几比几的比缩小呢？新的认知冲突诱使学生对图形放大与缩小的数学意义展开深入思考。结合对具体图形的观察，对照已经探索出的概念的理解，在对具体问题的比较辨析中，学生豁然开朗：“图形按照几比几放大（缩小）原来就是放大（缩小）后与放大（缩小）前对应边的比。”摒弃了面积比这一干扰。这次比较，使比的知识的特性更加清晰。

有比较才有鉴别，有鉴别才容易揭示规律、把握本质。在教学中找准学生的认知起点，精心选择对比的素材，适时、恰当地运用比较分析，能使学生深刻地理解概念的本质意义，知其然也知其所以然。这样既发展了学生的逻辑思维能力，又培养了学生运用所学知识解决实际问题的能力，使学生学得轻松、愉快，学得扎实，学习力悄然生长。

（责编金铃）