砂岩变形率与水理效应的力学特性研究

2020-05-15滕腾杜玉冰陈朋飞展鹏飞

矿业科学学报 2020年3期

滕腾，杜玉冰，陈朋飞，展鹏飞

1.中国矿业大学(北京)能源与矿业学院，北京 100083；2.煤炭安全与资源开采国家重点实验室，北京 100083；3.深部岩土力学与地下工程国家重点实验室，江苏徐州 221116

岩石的变形扰动过程与含水状态对其力学性质具有重要影响，任何岩土工程的设计与实施都必须把工程扰动和水文条件纳入考虑范围之内。

国内外学者对岩石的变形率效应进行了大量研究，并获得了诸多成果。尹小涛等[1]通过0.000 5 m/s、0.001 m/s、0.005 m/s和0.05 m/s 四个加载速率下的单轴压缩数值试验，分析了加载速率对岩石破裂形态、裂纹数量和扩展、应力-应变曲线和能量转换的影响，发现加载速率会造成岩石材料破坏形态的改变，材料破坏过程中存在塑性向脆性转变的临界速率。Wasantha等[2]研究了不同应变率下含不同颗粒尺寸砂岩的力学行为，发现砂岩的抗压强度随加载速率的增加呈增大趋势，其原因为颗粒破裂导致的应力重新分配。Gong等[3]研究了不同加载速率下煤岩组合体的力学性能，结果表明煤岩组合体在高加载速率范围内的动应力-应变曲线具有双峰特征。苏承东等[4]利用RMT-150B岩石力学试验系统，对义马曹窑煤矿顶板砂岩进行单轴、三轴压缩与声发射试验，指出岩样压缩变形破坏过程中的声发射参数与加载方式有关。宋义敏等[5]开展了不同加载速率下含Ⅰ型预制裂纹花岗岩试件的三点弯试验，研究表明花岗岩试件初始裂纹扩展速率随着加载速率的增加总体呈线性增大趋势。杨仕教等[6]定量分析了加载速率对石灰岩试件单轴抗压强度、峰值强度以及相应的应变、破坏形态、应力-应变关系等物理力学性态的影响，指出随着加载速率的提高，石灰岩的峰值强度线性增大。Hashiba等[7]通过砂岩试件在反复改变应变率条件下的压缩试验，发现砂岩的峰值强度与残余强度对应变率有依赖性。梁昌玉等[8]以若干硬质岩石试件在不同应变率加载条件下的试验数据为依据，研究了岩石材料在静态和准静态加载下的应变率临界值。Brantut等[9]通过多种脆性岩石压缩试验，建立了岩体微裂纹性质与应变率之间的关系。

此外，学者研究了水对岩石力学性质的影响。许江等[10]利用自主研发的煤岩细观剪切试验装置和声发射测试系统，研究3种不同含水状态下砂岩剪切破坏过程中的声发射特性，指出声发射活动伴随着砂岩整个剪切破坏过程，表现为剪应力峰值前声发射活动不显著，声发射信号均较小，而在剪应力峰值后声发射信号出现剧增。茅献彪等[11]试验研究了煤层冲击倾向性、煤层含水率和煤层孔隙率之间的关系。张娜等[12]分析了深部煤系页岩吸水软化效应的微观机理。Vásárhelyi和Ván[13]进行了砂岩的抗压强度对水的敏感性分析，确定了水对岩石强度的弱化效果。李鹏等[14]发现含水率是影响岩石软弱结构面蠕变特性的重要因素，并通过不同含水率下的剪切蠕变试验进行验证和分析。李尤嘉等[15]从细观力学的角度分析了水对岩石破裂全过程的影响。Tórók和Vásárhelyi[16]对比了饱水岩石和自然干燥岩石的密度、超声波速度、有效孔隙率和单轴抗压强度，利用统计学方法进行了分析。秦虎等[17]探讨了不同含水率下煤样受压变形破坏过程中的声发射特征，发现含水量的增加使声发射累计振铃计数减少，并产生明显的声发射时间滞后。

尽管众多学者进行了大量研究，但针对砂岩变形率效应和水理效应的评价指标与定量研究仍有许多工作需要做。本文利用MTS815.02电液伺服试验系统与PCI-2型声电数据采集系统进行了干燥和饱水砂岩的单轴压缩试验，对比分析了不同加载速率下2种砂岩力学参数的强化和弱化特性，并结合声发射特征建立了砂岩的一维本构模型。研究结果可对预测和评估岩土水力学、动力学等工程应用提供借鉴。

1 试验过程

采用中国矿业大学深部岩土力学与地下工程国家重点实验室MTS815.02电液伺服试验系统和PCI-2型声电数据采集系统，开展不同变形加载速率下干燥和饱水砂岩试样的单轴压缩和声发射试验。

试验采用的红砂岩质地细腻均匀，结构粒径较细，呈现褐红颜色。砂岩试样为直径50 mm、高度100 mm的圆柱体，端面平行度小于 0.05 mm，平面度小于0.02 mm。干燥岩样105 ℃烘干24 h以上，测得平均密度为2.44 g/cm3；饱水岩样纯水浸泡不少于24 h，直至不再增重，达到自然饱和状态，测得平均密度为2.47 g/cm3，饱和含水率为1.62%。图1为试验所用的测试系统与部分砂岩试样。

图1 试验设备与样品加工Fig.1 Test equipments and shaped specimens

试验采用位移控制加载方式，针对目前岩石静态压缩试验大多采用的变形加载速率，拟定变形加载速率分别为：0.05 mm/min、0.1 mm/min、0.2 mm/min和0.3 mm/min，研究该范围内干燥和饱水砂岩的变形率效应，每个速率下重复3组。根据本次试验环境的噪声水平与以往工作经验[18]，设定声发射信号去噪阈值为45 dB，数据采集定时参数为PDT=50 μs，HDT=200 μs，HLT=300 μs。

2 试验结果分析

2.1 全应力-应变曲线对比分析

图2为不同变形加载速率下干燥和饱水岩样的全应力-应变曲线。观察图2(a)可知，干燥岩样的应力-应变曲线可大致分为3个阶段：弹性变形与微弹性裂隙稳定发展阶段(OA段)，此阶段在整个应力-应变曲线中占80%～90%，应力与应变呈线性关系；非稳定破裂发展与弱塑性阶段(AB段)，占全程曲线的10%左右，仅出现在岩石峰值强度前期，表明岩样出现不可恢复塑性变形；失稳破裂阶段(BC段)，此阶段不足全程曲线的10%，经过变形累积，当外载超出岩石极限抗压强度时，岩样脆性破裂，抗压能力直线下降。

观察图2(b)可知，水对砂岩应力-应变曲线的影响主要有两个方面：一是出现较长压密阶段(OA段)，此阶段应力-应变曲线呈下凹状；二是岩石弹性阶段(AB段)缩短，塑性阶段(BC段)增长，表明岩石的弹性变形能力减弱，塑性变形能力增强。分析以上原因，砂岩中水的存在降低了矿物颗粒表面黏聚力，加剧了骨架颗粒间的细观错动与滑移，加强了微观晶体间的位错塞积。宏观上则表现为岩体变形的应变软化，峰后应变增大，砂岩由脆性向塑性转化。

图2 不同变形加载速率下干燥和饱水砂岩的全应力-应变曲线Fig.2 Stress-strain curves for dry and water-saturated rock specimens under different deformation rates

2.2 砂岩抗压强度的率效应与水理效应分析

图3(a)为干燥和饱水岩样单轴抗压强度随加载速率的变化曲线。从图3(a)可知，砂岩的抗压强度随加载速率的升高而依次增大，说明变形加载速率对干燥和饱水砂岩的抗压强度均具有强化作用。由于水能降低砂岩颗粒表面黏聚力，相同加载速率下，饱水岩样的抗压强度均小于干燥岩样的抗压强度，水的存在对砂岩强度起到弱化作用。

定义砂岩抗压强度的率效应强化因子μsv为高变形加载速率下砂岩强度σsv与低变形速率下砂岩强度σsv0的比值，砂岩抗压强度的水理效应弱化因子μsθ为饱水砂岩强度σsθ与干燥砂岩强度σsθ0的比值，即

(1)

(2)

图3(b)为不同加载速率下砂岩抗压强度率效应强化因子和水理效应弱化因子的演化图。结合图3(a)可知，对于干燥岩样，当变形加载速率由0.05 mm/min依次增加到0.1 mm/min、 0.2 mm/min和0.3 mm/min时，岩石抗压强度由52.9 MPa依次增大为54.7MPa、58.9 MPa和64.3 MPa，抗压强度的率效应强化因子依次增大，

图3 砂岩抗压强度的率效应与水理效应分析Fig.3 Effects of deformation rate and water saturation on the compressive strength of sandstone

分别为1.03、1.11和1.21；对于饱水岩样，当岩样抗压强度由45.2 MPa依次增加到47.4 MPa、52.4 MPa和60.9 MPa时，强度率效应强化因子依次增大，分别为1.06、1.16和1.35，且增长速度大于干燥岩石。砂岩抗压强度的水理效应弱化因子分别为0.85、0.87、0.89和0.95，且随着加载速率的增大而增大。当加载速率逐步增大时，干燥岩样和饱水岩样抗压强度的差值逐渐减小，其原因为砂岩强度水理弱化效应和变形率强化效应竞争作用的结果。水降低了砂岩颗粒表面黏聚力，在低变形速率下，砂岩强度的水理弱化效果比较明显；随着加载速率的提高，砂岩的饱水弱化效应被变形率强化效应掩盖。

2.3 砂岩弹性模量的率效应与水理效应分析

图4(a)为干燥和饱水砂岩弹性模量随加载速率的变化曲线。从图4(a)可知，加载速率对砂岩弹性模量具有显著强化效果：对于干燥岩样，当变形加载速率由0.05 mm/min依次增大为 0.3 mm/min时，砂岩弹性模量由13.4 GPa，依次增大为14.6 GPa、15.1 GPa和16.9 GPa；对于饱水岩样，弹性模量则由11.0 GPa，依次增大为11.6 GPa、 12.3 GPa和13.7 GPa。相同加载速率下饱水岩样的弹性模量低于干燥岩样的弹性模量，表明水对砂岩弹性模量具有弱化作用。

类似地，定义砂岩弹性模量的率效应强化因子μEv为高变形加载速率下砂岩弹性模量Ev与低变形速率下弹性模量Ev0的比值，砂岩弹性模量的水理效应弱化因子μEθ为饱水砂岩弹性模量Eθ与干燥砂岩弹性模量Eθ0的比值，即

(3)

(4)

通过式(3)和式(4)，计算不同加载速率下砂岩弹性模量的率效应强化因子和水理效应弱化因子，如图4(b)所示。由图4(b)可看出，当变形加载速率由0.05 mm/min依次增加到0.3 mm/min时，干燥岩样的弹性模量率效应强化因子分别为1.09、1.13和1.26，饱水岩样的弹模强化因子分别为1.05、1.12和1.25，两者都呈线性增长趋势；不同加载速率下，饱水砂岩与干燥砂岩弹性模量的比值基本保持不变，即不同加载速率下砂岩弹性模量的水理效应弱化因子变化不大，分别为0.82、0.80、0.81和0.81，即μEθ≅0.81，这说明对于文中设定的自然饱水砂岩，在试验的静态变形加载速率范围内，水对砂岩弹性模量的弱化作用不具有变形率敏感性。

图4 砂岩弹性模量的率效应与水理效应分析Fig.4 Effects of deformation rate and water saturation on the elasticity modulus of sandstone

2.4 砂岩峰后应变的率效应与水理效应分析

图5(a)为干燥和饱水岩样峰后应变随加载速率的变化曲线。可以看出，加载速率对砂岩峰后应变的影响较小，而饱水岩样的峰后应变普遍远大于干燥岩样，平均增大31.8%。分析以上原因：一方面，由于水对砂岩的软化作用，矿物颗粒本身塑性变形能力增强，压密阶段增长；另一方面，矿物颗粒表面黏聚力降低，导致颗粒之间错位或开裂所需的能量降低，砂岩内部脆性断裂单元减少，而塑性滑移单元增多，最终导致砂岩宏观塑性能力增强，即峰后应变增大。

类似地，定义砂岩峰后应变的率效应强化因子μev为高变形加载速率下砂岩峰后应变εev与低变形速率下砂岩峰后应变εev0的比值，砂岩峰后应变的水理效应强化因子μeθ为饱水砂岩峰后应变εeθ与干燥砂岩峰后应变εeθ0的比值，即

(5)

(6)

综上分析可知，砂岩峰后应变的率效应强化因子对加载速率并不敏感，即μev≅1；峰后应变的水理效应强化因子较大，且对加载速率的敏感性也不强，即μeθ≅1.32，如图5(b)所示。

根据式(1)至式(6)与本研究的试验，计算砂岩基础力学参数与强化、弱化因子的平均值，见表1。

表1 砂岩基础力学参数与强化、弱化因子

2.5 不同速率下干燥和饱水岩样声发射事件特征

图6和图7为不同加载速率下干燥和饱水岩样的应力-应变-声发射振铃计数率曲线。从图中可以看出，随着加载速率的增大，砂岩损伤破裂的声发射信号总量具有递增趋势，其中干燥砂岩的规律性较明显，而饱水砂岩的规律性较差。对于干燥岩样，声发射-应变曲线与应力-应变曲线有很好的对应关系：在弹性阶段，声发射信号很少，在塑性变形阶段和峰值前声发射聚集，随着峰后岩石应力跌落，声发射信号恢复到平寂状态；对于饱水岩样，岩石变形的压密阶段仍出现较多声发射信号，这是压密导致裂隙闭合期间内部排水，同时砂岩含水软化导致内部颗粒错动滑移的缘故。对比图6和图7中声发射事件计数率强度可以发现，干燥岩样声发射事件计数率的超大信号强度高于饱水岩样，而中小信号的强度小于饱水岩样。这是因为干燥岩样硬度大、脆性强，岩石颗粒破碎急促，能量释放剧烈且短暂，容易出现超强声发射信号，但中小强度信号相对少；反之，饱水岩样颗粒破碎强度略弱，但破碎之前的变形调整时间长，即破碎持续时间较长，因而中小强度信号较多。

图6 不同速率下干燥岩样应力-应变-声发射曲线Fig.6 Curves of stress-strain-AE for dry rock specimens at different deformation rates

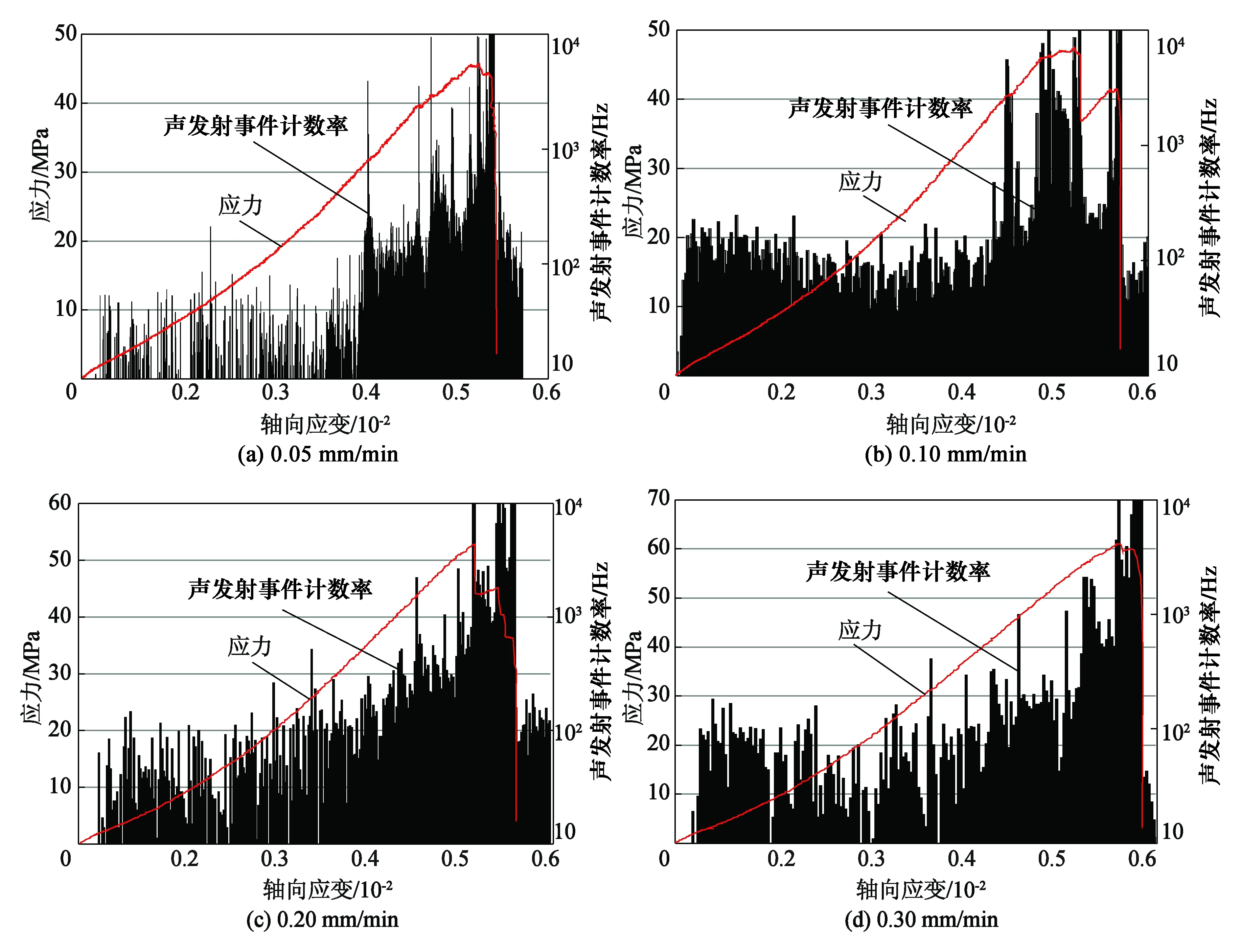
图7 不同速率下饱水岩样应力-应变-声发射曲线Fig.7 Curves of stress-strain-AE for water-saturated rock specimens at different deformation rates

2.6 不同速率下干燥和饱水岩样声发射能量特征

图8为干燥和饱水岩样的声发射能量累积与应变的关系曲线。对比图8(a)和(b)可看出，饱水岩样在加载到破碎整个过程中所释放的能量累积明显高于干燥岩样，是后者的3～5倍。这是因为饱水岩样的峰后应变较大，砂岩的能量释放时间长，由2.1节可知，饱水砂岩应力-应变曲线的延长阶段主要为压密、塑性和破坏阶段，此阶段的声发射信号多(图7)，对于能量累积的贡献较大；尽管饱水砂岩应力-应变曲线的弹性阶段缩短，但此阶段的声发射信号少，对能量累积的削弱作用可以忽略。由图6至图8可看出，砂岩声发射能量累积增长过程主要集中在砂岩变形的塑性阶段与峰值破坏阶段。考察塑性区砂岩声发射能量累积曲线的演化方式发现：干燥砂岩能量累积随变形加载速率的提高呈增大趋势，累积速度提前；饱水砂岩能量累积随着变形加载速率的提高呈减小趋势，累积速度推迟。该结果表明，砂岩饱水不仅克服了加载速率提升对砂岩声发射信号的增强作用，同时存在一个排水延迟过程。变形加载速率越大，相对于轴向应变的排水延迟越长，造成不同变形加载速率下饱水砂岩在塑性区内的声发射演化趋势与干燥砂岩完全相反。

图8 声发射能量计累积与应变关系Fig.8 Relationship curves of cumulative AE event rate to strain

通过以上分析可知，不同力学参量对砂岩变形加载速率和水理效应的敏感度并不相同。利用砂岩的峰值强度和弹性模量来衡量加载速率对砂岩的强化效应效果显著，利用岩石的全应力-应变曲线和声发射特征以及破坏时的峰后应变值能够较为准确地评价砂岩的饱水软化效应。

3 考虑率效应和水理效应的一维本构模型

3.1 一维本构模型构建

以上研究表明，变形率和饱水对砂岩的应力-应变曲线及声发射特征具有显著影响。因此，应考虑岩石变形率效应和水理效应，建立岩石本构模型。

利用声发射能量累积定义岩石损伤变量，其形式[19]为

(7)

式中，DΩ为岩石损伤变量；Ω为声发射能量累积数；Ωm为破坏后总的声发射能量累积数。

损伤岩石变形的经典一维本构模型为

σ=Eε(1-DΩ)

(8)

式中，σ为岩石应力；ε为岩石应变；E为岩石弹性模量。

根据等效应变假设，条件变化对岩石本构的影响可以通过弹性模量修正系数μE进行修正，即

σ=μEE0ε(1-DΩ)

(9)

显然，本文考虑的弹性模量修正系数μE为砂岩弹性模量的率效应强化因子μEv和水理效应弱化因子μEθ，即

μE=μE(μEv，μEθ)

(10)

考虑加载速率的影响，根据弹性模量的率效应强化因子的定义，干燥砂岩的一维本构模型为

σd=μEvE0ε(1-DΩ)

(11)

根据其定义，考虑水理效应的影响，变形率效应和水理效应的砂岩一维本构模型可进一步表示为

σ=μEθμEvE0ε(1-DΩ)

(12)

由2.3节分析可知，不同加载速率下砂岩弹性模量的水理效应弱化因子基本不变，即不同加载速率下式(12)中μEθ为常数。

3.2 模型验证

选取变形加载速率为0.05 mm/min的干燥砂岩试样作为参考，则初始弹性模量E0=13.4 GPa，考察加载速率分别为0.05 mm/min、0.1 mm/min、0.2 mm/min和0.3 mm/min的干燥岩样和饱水岩样，通过式(3)和式(4)(或表1)计算获得μEv和μEθ，通过图8计算损伤变量DΩ，代入式(12)，得到砂岩单轴压缩的应力-应变曲线。图9为试验结果与基于一维本构模型的理论结果的对比，由图9可知，两者具有很好的拟合度。