遥感图像拼接中改进的图像预处理算法研究∗

么鸿原 王海鹏 林雪原 潘新龙

（海军航空大学 烟台 264000）

1 引言

无人机具有体积小、时效性强、操作灵活、成本低等优点，其航拍遥感技术被广泛应用于灾害监测、环境侦察等方面［1～3］。遥感图像预处理作为无人机图像拼接的第一环节，其处理效果会直接影响到后续拼接的速度、配准准确度以及图像拼接质量。

受限于无人机的飞行高度低、体积小、重量轻导致的抗风能力差、数码摄像头焦距不足等因素的限制，无人机遥感技术所拍摄的图像往往像幅小、数据量大；虽然大多数无人机均装载了陀螺仪以稳定重心，但在无人机图像采集过程中无法避免的会因颠簸、抖动等因素引起航拍图像的几何畸变；并且数码相机的成像过程也有可能产生不同程度的几何畸变，这些变形会直接影响后续的图像特征采集与配准，因此在预处理过程中进行有效的畸变校正极为重要。除去畸变因素，无人机遥感图像还会受到诸多环境变量的影响，如光照、烟雾等，这也导致了即使是相邻多幅图像之间，也会存在较大的亮度差异和色调差异，这些也会影响到特征点检测的准确度以及最后图像融合的质量，因此在预处理阶段中引入匀光处理十分必要。在任何图像采集过程中，噪声干扰都是需要考虑的因素，本文所提出的基于图像锐化的平滑处理能够有效地去除噪声并增强图像细节［2］，为下一步特征配准打下良好的基础。

2 航拍图像的畸变校正

在无人机图像采集过程中受飞行因素或相机因素影响，图像中的整体或局部有可能会存在一定程度的几何畸变，因此在预处理过程中进行有效的畸变校正极为重要。

畸变校正又称几何校正，指的是消除图像中几何变形的过程。其主要包含两个步骤［4］：1）建立畸变图像与未畸变图像之间的映射关系；2）对未畸变图像进行重采样。

畸变校正所需的数据可以通过查询相机参数获得，设径向畸变系数为K1、K2，像主点的坐标为O(x0，y0)，偏心畸变参数为 P1、P2。假设 P(xi，yi)为畸变图像中的一个像素点，则像素点的坐标变形可以由式（1）表示。

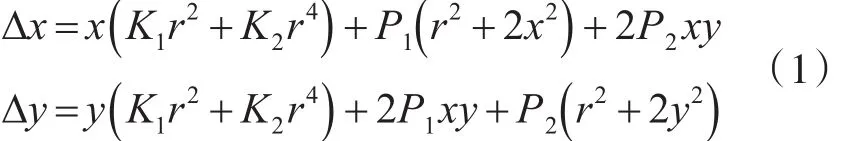
其中，x=xi-x0，y=yi-y0，r2=x2+y2。

因此，如果畸变图像中P点在畸变矫正结果中对应的点为 P′(xj，yj)，那么，P′的坐标可由式（2）求出。

确定了畸变前后图像的映射关系后，由于映射到畸变矫正结果上的像素点不一定是整数点，所以需要对畸变校正后的图像进行重采样。设畸变图像的像素点P，在校正结果中对应的点P′的坐标是(i +u，j+v)。式（3）表示的是 P′的像素值。其中，i，j代表像素点行和列的整数部分，u，v是相应像素点的小数部分。

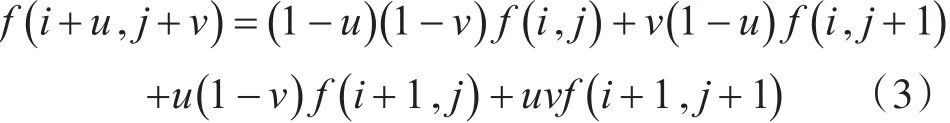
式（3）中 ， f(i ， j) ， f(i +1，j) ， f(i ， j+1) ，f(i +1，j+1)分别为畸变图像上像点 P1，P2，P3，P4的像素值。利用式（3）可以完成对畸变图像的校正。

图1为航拍图像畸变校正的原图和校正结果。由图1可以看出，经过畸变校正，图像中线条的曲度发生较为明显的变化。由此说明了本文提出的畸变校正算法真实有效，能够很好地实现畸变图像的校正。

图1 畸变校正前（左）后（右）对比图

3 航拍图像的匀光处理

航拍图像由于受到云层、烟雾、光照等影响，在亮度、色调、反差等方面存在一定差异，这种差异叫做不均匀光照。而不均匀光照对特征提取存在一定影响，同时也会对图像融合造成一定程度的影响［5］。所以在图像预处理过程中需要对航拍图像做匀光处理。图像的直方图代表的是图像的统计特征，它代表的是数字图像中每一灰度级与该灰度级出现的像素数或频数之间的数学统计关系。相邻的两幅航拍图像由于拍摄位置、时间的差异可能会导致其直方图也存在很大区别。但是，理论上说，相邻两幅航拍图像存在一定比例的重叠部分，直方图的相似度应该很高［6］。所以，可以在图像预处理的过程中，通过采用直方图配准的方式使相邻两幅航拍图像的直方图趋于一致，由此完成两幅图像间的匀光处理。采用直方图配准的方式进行匀光处理的基本思想是：首先计算出参考图像的直方图，然后根据参考图像的直方图信息对待校正图像的直方图进行校正，使得待校正图像的直方图与参考图像的直方图大体上趋于一致，最终实现航拍图像的匀光处理［7］。图2中两幅图像分别为参考图像和待校正的图像，可以明显看出两幅图像的光照不一致。

图2 参考图像（左）和待校正图像（右）

其中，参考图像和待校正图像对应的直方图如图3所示。从图3中可以看出，两幅图像的直方图形状大体上相似，但是参考图像的直方图像素频数分布更加均匀，待校正图像的直方图像素集中在中部，两边的像素比较少。这说明两幅图像还在色调和亮度上存在一定差异，有必要对待配校正像进行匀光处理。

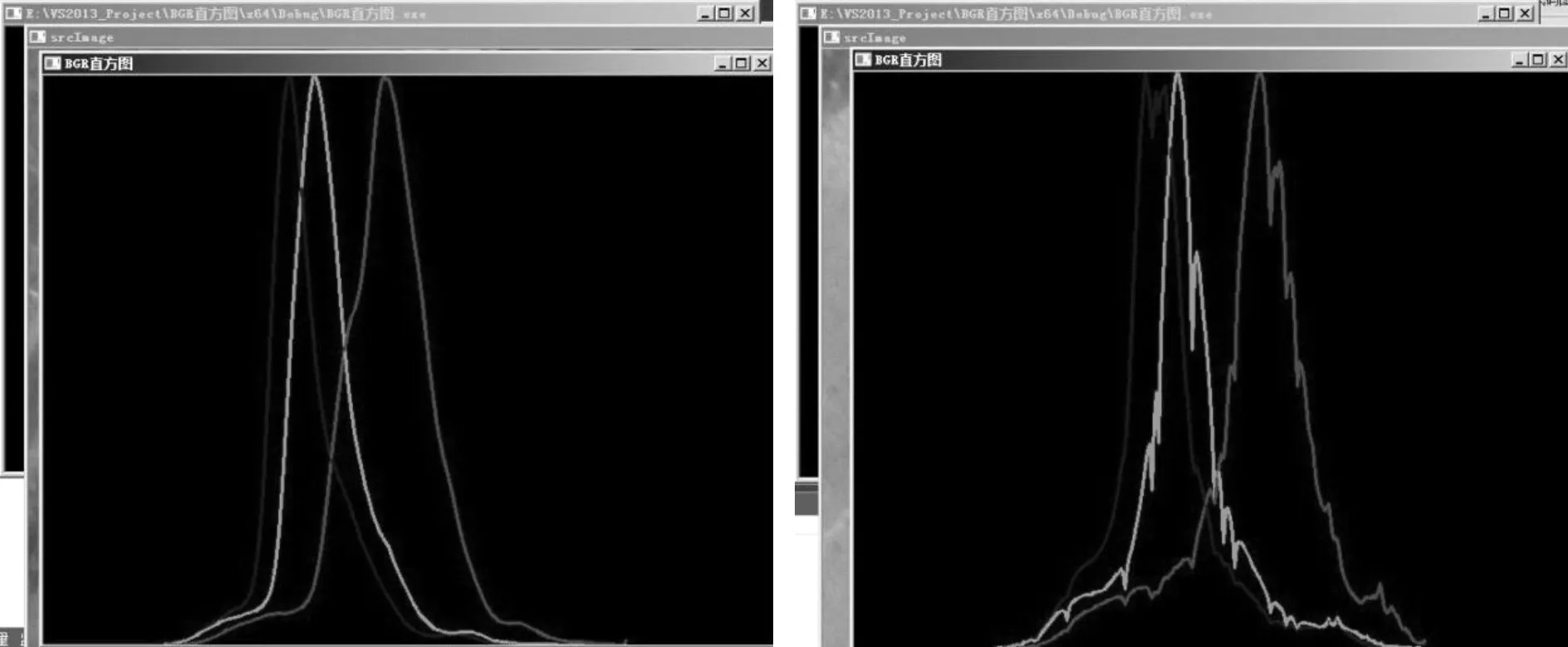
图3 参考图像（左）与待校正图像（右）的直方图

根据参考图像的直方图，对待校正图像进行匀光处理，可得到匀光后的图像以及其对应的直方图，如图4所示。从图中可以看出匀光校正［8］后的图像和参考图像在色调和亮度上更加一致，处理结果对应直方图的分布也更加均匀，达到了预期的效果。

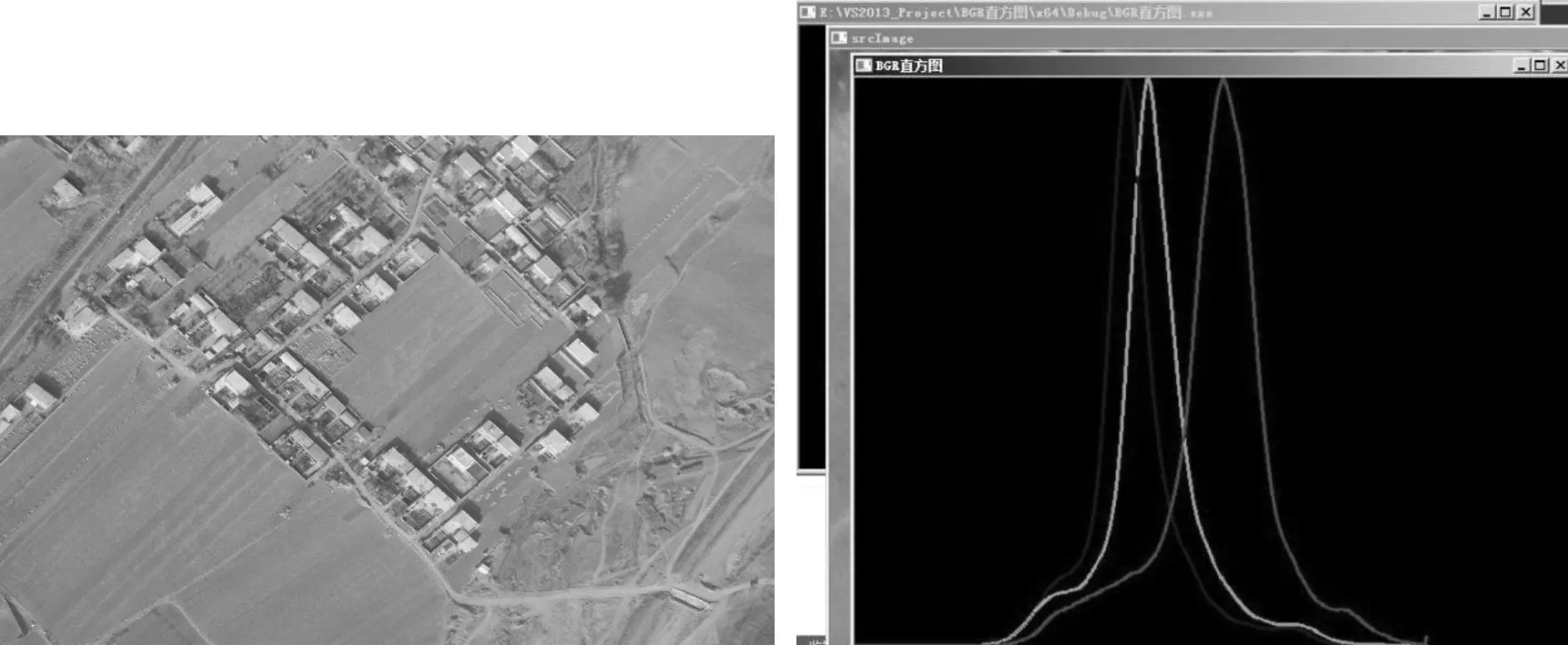
图4 匀光校正结果图（左）与校正后直方图（右）

由实验结果可以观察到，根据参考图像的直方图，对待校正进行直方图配准，配准后的结果在色调和亮度上与原始图像相比产生了明显变化，与参考图像的色调和亮度更加接近。同时，参考图像和待校正图像的直方图分布也存在很大差异，而经过配准后的图像在直方图分布上和参考图像也更为接近。由此可以看出，利用本文直方图均衡方法可以很好地实现对原始的航拍图像进行匀光处理，使航拍图像色调和亮度更为接近，直方图分布也更为一致，实验效果较为理想，具有一定的可行性。

4 改进的平滑处理

无人机航拍所采集的遥感图像可能会受到噪声干扰，如高斯噪声、椒盐噪声等；噪声的存在会对接下来的特征提取的速度与特征配准的准确度造成一定的影响，影响图像拼接结果，因此我们需要进行有效的处理以消除图像中的噪声干扰［9］。图像平滑是指直接对源图像数据做空间变换以达到平滑的目的［3］，这种计算通常也被称作模糊或滤波，常见的平滑处理有盒滤波、均值滤波、中值滤波、高斯滤波、双边滤波等［10］。

均值滤波又称邻域平均法，算法简单，计算速度快，但不能很好地保护图像细节，在去噪时也破坏了图像细节和边缘信息导致图像模糊。中值滤波在边界的保存方面优于均值滤波，画面清晰度基本得到保持，但在图像模板太大时，仍会存在一定的模糊［11］；相对于均值滤波和中值滤波，高斯平滑的平滑效果更柔和，而且边缘保留的也更好［12］。因此本文选择高斯滤波法作为平滑方法并进行改进。

高斯滤波是将输入数组的每一个像素点与高斯内核进行卷积计算，将卷积和作为输出像素值。假设构造宽（列数）为W、高（行数）为H的高斯卷积算子gaussKernelH×W［13］，其中W和H均为奇数，锚点位置在，计算高斯矩阵如式（4）所示，其中gaussr，c代表位置索引，且r，c均为整数。

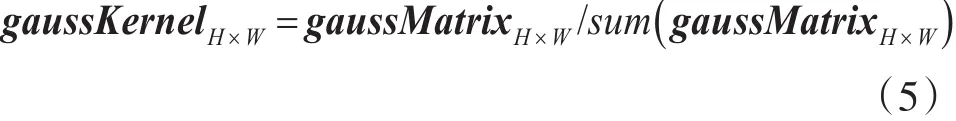
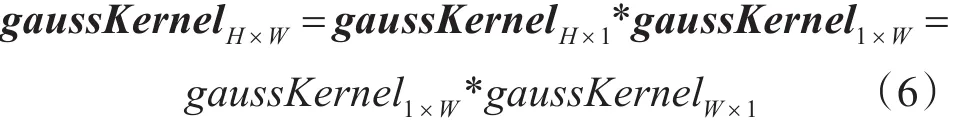
所以在对图像进行高斯平滑时，可以根据same卷积的结合律和卷积核的分离性对图像先进行一维水平方向上的高斯平滑［14］，然后在进行一维垂直方向上的高斯平滑，反过来也可以；因此高斯平滑的平滑效果更柔和，边缘、细节等信息保留的也更好。

高斯平滑处理结果如图5所示，从图中可以看出，高斯滤波能够消除图像中的孤立点与线段，并且较好的去除高斯噪声及椒盐噪声（受篇幅限制，本文只给出高斯噪声滤波结果）。

图5 带有高斯噪声图像平滑前（左）后（右）的对比

对于无人机遥感图像拼接而言，高斯平滑后虽然能够去除图像中的噪点，但是通过将图像转化为灰度图并放大后，可以发现多次的高斯平滑处理，会导致图像对比度较低，图像中的细节变模糊，且在图像拼接中，接下来还会通过构造高斯金字塔［15］来完成特征检测与提取，在这一步骤中还会进行多次平滑处理，这将会导致图像平滑过渡，对比度更低，细节更加模糊，反而使特征点提取数目变少，配准准确率变低；因此，我们需要对平滑处理算法进行了相应改进。

由前面提到的平滑处理可知，图像的模糊受到两方面影响：1）图像自身因素；2）平滑处理过程中对图像数据进行了一系列运算。从第二点出发进行考虑，若想增强平滑后图像的细节，那么对平滑后的图像进行与平滑算法相对应的反向运算即可，即对高斯平滑后得到的图像I( )x，y与矩阵F进行卷积，如式（7）所示，此时得到的新图像通过放大观察细节发现明显清晰了许多的同时，噪声点也并未出现。

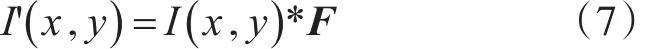
式（8）中的F为自定义的锐化滤波器，其实质上是一种微分算子。

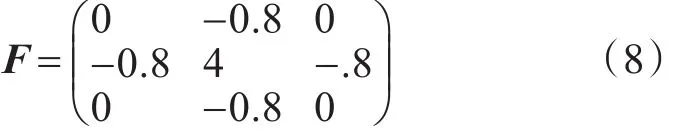
操作结果对比如图6所示。

图6 灰度图像锐化滤波前（左）后（右）对比图

5 结语

本文主要研究了航拍图像预处理中遇到的图像噪声大、光照差异大、视野中景物存在畸变、图像不清晰等问题。通过分析航拍图像产生畸变的原因，找到了校正畸变的方法，并验证了畸变校正算法的有效性。然后采用直方图配准法对原始图像进行了匀光处理，实验表明，本文采用的直方图配准法能够有效地统一两幅航拍图像的色调和亮度，达到了预期的效果。最后针对遥感图像经平滑去噪后图像细节不明显的问题，提出了基于图像锐化的高斯平滑处理，增强遥感影像的细节。实验表明，改进的高斯平滑算法可以有效地消除图像中的噪声，并能够很好地保留图像边缘信息，获得较理想的效果；在后期进行特征提取时，采用本文所提预处理算法后提取到的特征点数目比起采取其他常规图像预处理算法后提取到的数目平均增加了约16%左右，下一阶段应重点对算法运行时间进行研究改进。