S曲线加减速控制在数控机床研究中的应用进展*

韩业鹏，王孝伟，陈从桂，沈 腾，朱厚耀，贺香华

（广州大学机械与电气工程学院，广州 510006）

0 引言

数控机床（CNC）首先在美国诞生。1948年，帕森斯公司开发出一种处理直升机叶片轮廓检测的机床，提出了研制数控机床的初步设想。1949年，帕森斯公司和美国的高等学校进行交流与合作。1952年，全球第一台数控机床问世，是三轴数控铣床，其硬件系统用电子管来实现。自1960年以来，德国和日本等国家先后开发、生产和使用了数控机床。1968年，北京第一机床厂开发出第一台数控机床；1974年，微处理器直接应用于CNC，进一步加快了数控机床的推广应用。由于计算机技术和电子技术的不断革新，CNC的数控系统也一直在发展，经历了以下几代变化。

（1）第一代数控（1952～1959）CNC的硬件数控系统是用电子管制作的；（2）第二代数控（1959～1965）是基于晶体管电路的硬件电路系统；（3）第三代数控（始于1965年）使用中小型集成电路的硬件控制系统；（4）第四代数字控制（始于1970年）是小型通用电子计算机数控系统，采用大规模集成电路；（5）第五代数控（始于1974年），其在计算机数控系统的控制是小型控制；（6）第六代CNC（始于1990年）使用通用数控系统用于工业PC。其中，CNC主要由硬件和软件构成，硬件联动结构组成称为硬件数控；计算机数控主要由软件完成。近20年以来，随着国家经济水平和科技创新能力的提高，国家的工业与制造业也在发展，数控机床的应用越来越广泛。

目前，S曲线加减速技术在数控机床中比较稳定，所以本文主要论述S曲线加减速技术在数控机床中的相关应用与研究。

1 S曲线加减速的应用和原理

1.1 加减速在数控机床的应用

数控处理的目的是要达到高速度和高精度，这需要机床具有更高的加工速度，才不会损坏机床和刀具。目前，有很多技术可以实现这一目标，包括生成具有所需的加速和减速（acc/dec）特性。加减速可分为几种常见类型，其中线性加减速[1-2]是最简单、最容易实现的，但是其速度的突变会导致加速曲线不够平滑[3]；而指数加减速[4]具有强大的跟踪能力，但是在高速时稳定性较差、计算方式相对复杂[5]。

为了避免线性加减速的限制，对非均匀的弦误差和有理样条曲线（NURBS）等参数插值器提出了不同的约束组合。Yong等[6]和Du等[7]考虑弦误差和切向加速度分量极限；Feng等[8]考虑了弦误差和加速度极限；Du等[9]、Emami等[10]和Annoni等[11]考虑了弦误差、加速度和加加速度限制的切向分量；Lai等[12]、Tsai等[13]和Lee等[14]考虑弦误差、加速度和切向抖动限制。在双轴加工中，大多使用现有的参数插值器处理几何误差。但是，由于需要2个额外的旋转轴，随着复杂性和五轴加工中的约束数量，计算负荷会明显增加[15]。S曲线加减速具有三角形加速度曲线，因此是S型的速度分布。S型加减速同线性和指数加减速相比较，能生成更平滑的命令，有更好的准确性。此外，其计算量加载比参数插值器少。

2001年，S曲线加减速控制问题由Altintas等[16]首次提出。随着现代数控系统的发展，加减速控制方法引起了相当多的关注。Chen等[17]提出了一种具有S曲线的前瞻算法连续线性/圆形段的加减速。Wang等[18]提出了一种离散S曲线速度控制算法线性段。除了线性和圆形段，S曲线加减速也适用于NURBS工具路径。Lin等[19]根据尖角和预定的信息将NURBS路径划分为小段，其中的小段属于S曲线加减速的多个速度曲线。Heng等[20]开发了一种光滑连续的进给模态，采用S曲线和钟形曲线acc/dec进行多段NURBS刀具路径模拟。

1.2 S曲线加减速的原理

S曲线加减速法是根据系统加减速过程中速度曲线的形状推导出来的，是一种速度变化非常平稳的加减速运动控制算法。S曲线加减速的加速度是连续变化的，速度变化也比较柔和，能够有效减小冲击和振荡[21]。运动曲线的过程可分为7个阶段：加加速段、加速段、匀加速段、减速段、匀速度段、加减速段、匀减速段。其中，加加速段、减速段、加减速段、减速段的作用是防止力或加速度突然变化，减少冲击；匀加速段和匀减速段的作用是使其具有最大的力或加速度极限；匀速段的目的是存在最大速度的约束。

S曲线加速减速指的是加速和减速过程中，导数J在加速和减速的加速度是恒定的，和加速度控制导数，避免突然改变的加速度，从而减少了机械系统振动突然改变造成的加速度在加工过程中。采用S曲线加减速算法可以获得平滑的速度和加速度。

2 S曲线技术

2.1 加减速控制

常用的加速和减速控制规律有很多种，如直线型加减速和S型曲线加减速等。国内的郭新贵[22]和赵国勇[23]利用三角函数构造了基于j控制的新的加减速曲线。这些加减速控制的特点如下所述[24-27]。

（1） 梯形加减速控制运用数学公式简单、占用时间短、机器反应快，具有高能和高速的特点；缺点是对机床运动有柔性冲击，速度转换不够平稳、运动精度低。

（2） S曲线加减速的控制方式是让速度没有波动，加速度的变化也是稳定的。速度是加速度的积分，加速度是加加速度的积分，顾名思义，控制加速度的变化是重要的。S曲线加减速能够让加速度更加稳定，让机床运行得快而平稳，也不会有撞击；但该计算量比较大，难度较高。

（3）正弦加减速曲线与S型速度曲线相比，正弦加速和减速可以实现平稳运动，这相对简单且易于实现。

现代工业领域用梯形速度曲线控制方法比较多[1，28]，其结构简单、计算方便，广泛应用于控制精度较低的控制系统中。梯形速度曲线以加减速为特征，加速度为一个固定值，其值是人为定值。给出一个真实的加工轨迹，如果给定每个加工点的位置、加工过程的速度，并设置加速度值，就可以得到一个完整的梯形速度曲线。

图1为梯形速度曲线，包括速度曲线、加速度曲线以及加加速度曲线（jerk曲线）。梯形的速度曲线可分为简单的3个部分，即加速度增加部分、匀速运动部分和加速度减小部分，加速度增加部分和加速度减小部分的加速度大小相等。由图可知，速度曲线为典型的梯型速度曲线，因此在加速度的变化处就会产生一定的脉冲，会让正在加工中的数控机床有抖动，危害很大，严重损害机床的使用寿命，影响工件的加工精度。

图2所示为正弦加减速曲线示意图。其中，amax是最大的加速度；v1为开始的进给速度；v2为结束时的进给速度。正弦加减速算法比直线型加减速算法更好，正弦曲线中的加速度没有波动、更稳定，能够达到机床的运动精度，但是计算量大。正弦型速度曲线和S型速度曲线所表达的相差不大，不同的是正弦曲线的加速度是正弦曲线固有的[29-30]。正弦的速度曲线划分为3个部分，即加速段、匀速段和减速段。正弦的加速度曲线是速度曲线的导数。正弦速度曲线与S型速度曲线相比较，在让速度达到稳定的情况下，也减少了速度曲线的段数，速度曲线依然具有平滑性，比S型速度曲线的复杂性要低，更容易应用在实际数控中。

S型速度曲线是工业常用的速度控制方法，可以解决梯形速度曲线的一些缺点。S型速度曲线可以控制加速度的变化率。此外，S型速度曲线的加速度曲线在速度接合处是连续且平滑地过渡。因此S型速度曲线是一种能限制震动的速度控制方法[31-33]。

图3所示为S型速度曲线，可以分成3个部分，即速度曲线、速度曲线每个段所对应的加速度曲线、加加速度曲线。S型速度曲线匀速段的最大速度为vmax；起点速度为vstr；停止速度为vend；达到的最大加速度为amax；加速度的导数为J（加加速度）。

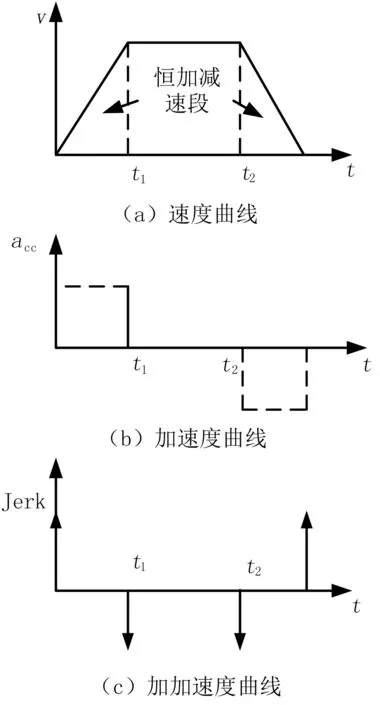
图1 梯形速度曲线

图2 正弦速度曲线

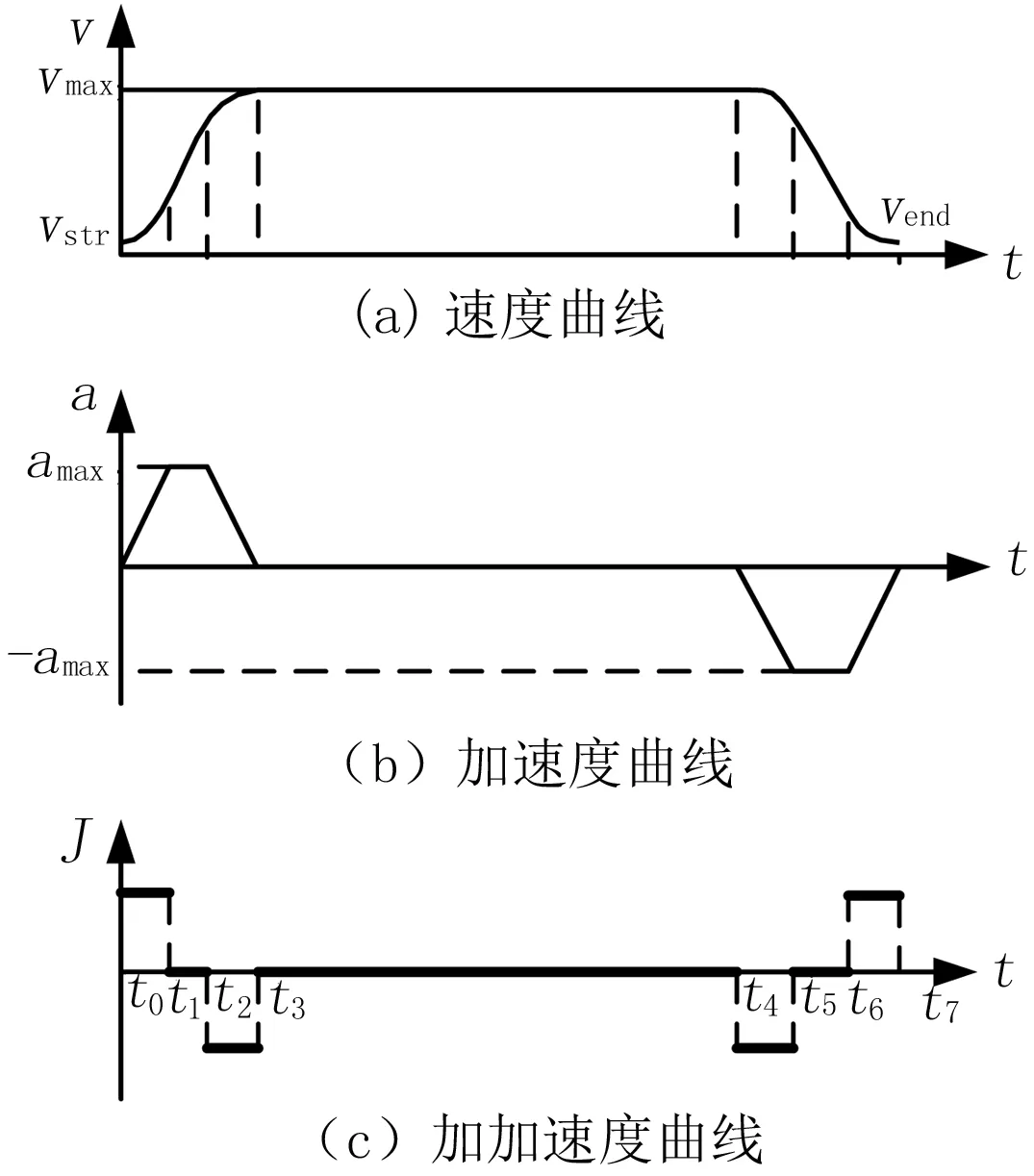
图3 S速度曲线

2.2 S曲线算法

形状比较复杂的工件加工一直是数控机床研究的难点和重点。传统的CNC加工系统使用离散化直线逼近曲线，其显而易见的不足是形成速度分布的曲线间断和波动较大，并且形成的数据量较多；另外，重复使用加减速产生轨迹会对机床带来很大的冲击，难以满足高速、高精度加工的要求。为了更好地解决此类难题，提高加工稳定性与零件表面加工质量，许多专家和学术界的领军人士产生了对数控使用曲线插补方法的想法。Shpitalni M[34]参照Taylor展开式来编写一阶和二阶的参数曲线插补方法，体现了稳恒参数插补的良好特性；Yeh S等[35]提出弦高误差的自适应参数曲线插补算法；Yong T等[6]在控制弦高误差的同时规划了数控加工过程中的加减速问题。然而，这些研究的内容主要集中在插补过程中插补点的计算，在插补过程中，并没有深入去探索加速和减速问题。

此外，一些专家也研究了NURBS插补的加减速。如Xu-Rongzhen等[36]提出了一种自适应的前瞻插补算法，同时对速度自适应控制也要进行前瞻控制，找到速度变化范围的容许值和不容许的范围值，再进行加减速变化；王海涛等[37]在S型加减速离散采样模型的基础上，提出了一种S型加减速前瞻算法；在加速度恒定的条件下，周胜德等[38]提出了一种基于NURBS曲线插补的5段S曲线加减速控制方法，解决了插补之前的加减速控制中难以预测减速点的问题。S型速度曲线具有连续的加速度变化，可有效地减弱对系统的冲击和振动。此外，每段的平稳加速和减速将使系统运行更加平稳。

2.3 S曲线数学模型

数学模型已广泛应用于社会、经济和科学等各个领域，显示出强大的生命力。数学模型在解决特定的实际问题方面具有优势。首先，数学模型为原型提供了简洁的形式语言。使用数学符号、图像和公式来揭示原型的性质、规律和结构，以便人们可以掌握原型系统。其次，数学模型提出的数学问题的解完全依靠于数学的概念、命题、微积分方法和逻辑推理。

目前，有很多学者对S曲线数学模型进行相关研究。武小虎[39]分析了数控系统加减速控制方法的基本原理，通过对样条曲线的数据处理，建立了一个新的数学模型，完成了样条插补算法的设计。胡建华和廖文和等[40]对数控系统中的几种加速和控制曲线进行了研究，分别分析了该数控系统的梯形、S型和直线加减速曲线，比较这几种控制方法的优缺点及其应用场合，主要研究了速度时间曲线在步进电机驱动的经济型数控系统中的应用。结果表明，直线段逼近曲线算法可以显著提高步进电机驱动的经济型数控系统的性能；但缺点是加速度变化突然、机床冲击灵活、速度过度不够平稳，不适合高速数控系统。石川等[41]提出使用S曲线加减速算法来总结可能出现的8种S曲线加减速模式，速度和位移采用运动学公式，使算法变得复杂、计算时间长。

在此基础上，陈友东等[42]推导出S曲线离散采样迭代公式，但该算法不包括匀加速阶段和匀减速阶段。潘海鸿[43]总结了不同参数条件下的17种S型曲线加减速类型，但大多数可以组合成统一的数学模型。田军锋等[44]根据S型曲线的对称性、初始速度、最终速度的不同特点简化了算法，可以快速计划每个阶段的运行时间和MATLAB验证算法，这样可以获得平滑的速度和加速度轮廓。通过简化S形曲线的速度和位移公式，可以快速判断S形曲线的几个阶段，从而节省了前瞻模块处理时间和系统资源，使系统能够更有效地进行处理。上述S型加减速规划涉及对称S型加减速控制，起止速度相等。如果要使用这样的加减速，电机在处理每个线段时需要从零开始加速。电机在达到最大转速后，再从最大转速降至零，电机频繁启动，不仅影响加工效率，还会引起抖动或振动，严重影响加工精度。杨亮亮等[45]指出非对称S型加减速时间的规划在初始和末速度均为非零的情况下比较困难。将加速度曲线划分为7个时间段，分析了加速度变化时间方程，并将其简化为一维高阶方程。变化的单调性构造其平方函数，将其转化为一个单凸函数，然后利用牛顿迭代法求出其收敛值，并根据效率原理和加速度、速度约束条件进行修正。对于匀加速时间，直接根据其公式的特点，将其转化为二次方程进行规划，并根据效率原理和加速度、速度约束条件进行修正。对于匀速运动时间，直接根据函数进行分析。这样能够解决现有始末速度不为零的S型曲线加减速和不对称的时间规划过程复杂、繁琐问题，给出一种方便、简单、高效的加减速时间算法。

3 结束语

通过对加减速控制方法的分析可知，S曲线加减速控制在数控机床中的应用主要有3个方面。

（1）通过对速度曲线的分析比较，S曲线控制可以避免速度和加速度的突然变化，减少冲击，提高数控机床运动的平稳性。

（2）采用S曲线算法有效地解决了预插补加减速控制中减速点预测困难的问题。S型速度曲线加速度的变化是连续的，可以有效减弱对系统的冲击和振动。

（3）采用S曲线数学模型对数控系统的加减速控制进行分析，能够有效地了解当前对数控机床系统加减速算法的研究，以解决初始速度不为零对加减速时间的规划问题。随着科学技术的发展与进步，数控机床不断地创新与改进，在数控中应用到的算法也会不断地推陈出新，但对数控机床的研究分析也变得愈加复杂。对于数控机床新出现的问题，S曲线的控制方法会不断地完善，从而满足数控机床对加工精度、速度和稳定性的需求。