全桥三电平LLC谐振变换器的控制研究*

彭秋雨，赵葵银，周惠芳，熊 赛

（1.湖南工程学院电气信息工程学院，湖南湘潭 411104；2.湖南电气职业技术学院，湖南湘潭 411101）

0 引言

随着现代工业制造水平的提高，越来越多的仪器和设备都需要DC电源，在DC电源中LLC谐振电路凭借其谐振特性，实现了前级开关管零电压开通（Zero-Voltage Switching，ZVS），次级整流二极管零电流关断（Zero-Current Switching，ZCS），满足当今DC电源所需求的高效率[1]、高功率密度和体积小等苛刻条件。而在高电压输入领域，三电平LLC谐振电路对比于两电平LLC谐振电路，有效降低了开关管电压应力和输出电压的谐波含量而被广泛应用于工业生产之中。

在生产实践中，通常采取调节LLC谐振电路的开关频率来调节电路的输出电压和电流，但由于电路具有非线性的特点使得传统的线性控制方法难以达到较好的效果。而在一些文献中，提到了许多非线性的控制方法，例如自适应模糊控制、滑模控制和鲁棒控制等，但由于这些算法过于复杂而难以在工程实践中实现。文献[2]中提出状态平均模型用以消除电路非线性特性，但由于LLC谐振电路是一种随时间变化的非线性电路，使得此模型方法失效。文献[3]中，基于扩展描述函数（Extended Description Function，EDF）方法建立了LLC谐振电路的非线性状态模型，但这种方法一般不能给出确切的时间响应。

本文使用变压器二次侧电流来表示LLC谐振电路的谐振特性，提出了一种简化的线性模型。基于此模型，提出了具有次级电流反馈的双回路控制策略，用于控制LLC谐振电路。最后通过Matlab中Simulink模块搭建仿真模型，验证了控制方法的正确性和可行性。

1 全桥三电平LLC谐振电路工作状态分析

全桥三电平LLC谐振电路拓扑结构如图1所示，开关管（Q1～Q8），开关管外加电容（C1～C8），开关管寄生二极管（D1～D8），钳位二极管（D9～D12）实现输入电压钳位，飞跨电容C11和C12辅助外加电容进行充放电。谐振腔由谐振电感Lr、谐振电容Cr和励磁电感Lm构成[1]，其中Cr除了有谐振作用外还起到隔离直流的作用，同时又能平衡变压器磁通并防止饱和。变压器二次侧二极管（VD1～VD4）构成整流电路，输出电容Co用于滤波和稳压，当前级无输出时，能继续为负载供电[4]。

图1 全桥三电平LLC谐振电路

当开关频率fs工作在谐振频率fr附近时，前级开关管可以实现零电压开通（ZVS），后级整流二极管可以实现零电流关断（ZCS）。谐振频率定义为：

针对全桥三电平LLC谐振电路的8个开关管，有着许多的开关方式。文献[5]提出了斩波加移相控制方式，但导致谐振腔的输入电压既不是奇函数也不是偶函数，存在着较大的谐波。本文根据研究内容和LLC谐振电路的特点，将采用变频和变占空比的控制方法。一个开关周期内的主要工作波形图如图2所示，以图1中谐振电流iLr方向为正方向。

图2 全桥三电平LLC谐振电路主要工作波形图

时段1（t0～t1）：t0时刻，开关管Q1、Q2、Q7、Q8开通，此时谐振电感电流iLr流过开关管Q1、Q2，进入谐振腔，从开关管Q7、Q8流入负极。整流二极管开关管VD1、VD4导通，此时Lm电感电压被输出电压钳位，使iLm呈线性增加，Cr和Lr参与谐振。

时段2（t1～t2）：t1时刻，iLr与励磁电流iLm相等，此时变压器不再向二次侧传播能量，整流二极管VD1、VD4实现零电流关断（ZCS）。负载由输出电容Co供电，Cr、Lr和Lm参与谐振，因为Lm较大，导致谐振周期较长，iLr可认为保持不变。

时段3（t2～t3）：t2时刻，开关管Q1、Q8关断，此时iLr给开关管外加电容C1、C8充电，同时通过飞跨电容C11和C12分别对C4、C5放电。由于C1、C8的缓冲作用，使得开关管Q1、Q8零电压关断。当C1、C8上的电压达到Vin2时，钳位二极管D9、D12导通，则此时Vab=0。

时段4（t3～t4）：t3时刻，开关管Q2、Q7关断，此时i Lr给C2、C7充电，同时通过飞跨电容C11和C12分别对C3、C6放电。由于C2、C7的缓冲作用，使得开关管Q2、Q7零电压关断。由于此时iLr将比iLm小，导致变压器二次侧电流反向，VD3、VD2导通，此时Lm电感电压被输出电压钳位，使i Lm呈线性减小，Cr和Lr参与谐振。

时段5（t4～t5）：t4时刻，由于C3、C4、C5、C6两端电压均降为零，谐振电流iLr将流过寄生二极管D3、D4、D5、D6。则t5时刻开通Q3、Q4、Q5、Q6可以实现零电压开通（ZVS）[6]。

后半个切换周期与前周期相似，此不赘述。

2 基于EDF对谐振电路进行建模及简化

2.1 谐振电路的建模

三电平谐振电路是非线性的，而且满足扩展描述函数（EDF）分析非线性系统的条件[7]。为了方便分析问题，根据电路特性做出以下假设：

（1）所有开关管均为理想器件，忽略死区时间和器件内部电阻，输入谐振腔的电压类似于方波信号；

（2）谐振变量均为正弦波，忽略谐波；

（3）每个控制周期内所有谐振状态变量均达到稳定（因为控制频率远小于开关频率），在切换期间忽略每个谐振变量的动态响应，图3为LLC谐振电路的等效电路。

图3 LLC谐振电路等效电路图

图中iVD为整流电路的输出电流，基于图3等效电路图建立状态方程：

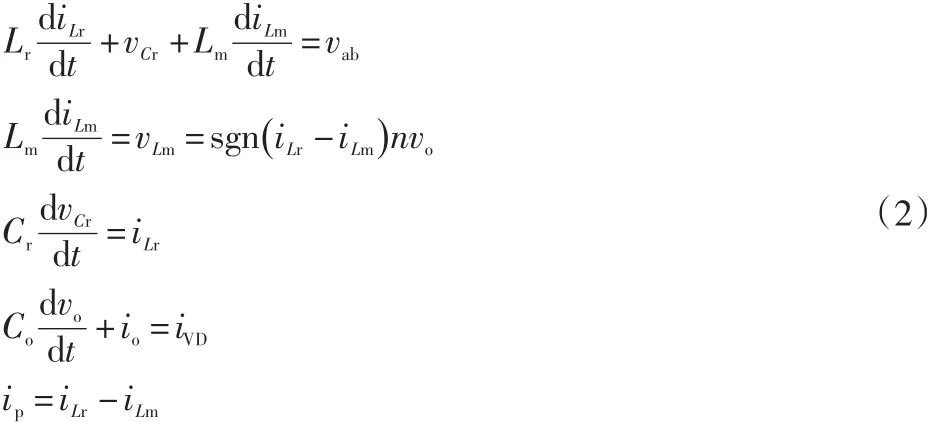
式中：vab、vo、vLm、vCr、iVD、io和ip分别为输入电压、输出电压、励磁电压、谐振电容电压、整流电流、负载电流和变压器原边电流。根据假设（2）和（3），谐振变量可以被分为正弦波和余弦波，如下所示：

式中：ILr1和ILr2分别表示谐振电流的正弦和余弦分量的幅度值；ILm1和ILm2分别表示励磁电流的正弦和余弦分量的幅度值；Ip1和Ip2分别表示变压器原边电流的正弦和余弦分量的幅度值；V Cr1和V Cr2分别表示谐振电流的正弦和余弦分量的幅度值。同理可列出vab和vLm的基波分量：

结合公式（2）～（4），用谐波平衡法消除正弦和余弦分量，可以导出正弦和余弦分量的幅度值状态方程：

基于扩展描述函数所建立的状态方程，仅仅只描述了电路的特性，并没有得到开关频率与输出电压之间的传递函数，不利于控制器的设计。

2.2 模型的简化

由于所建立的状态方程仍然是非线性的，且过于复杂，并没有给控制器的设计和分析提供帮助，因此需要对模型进行简化。

从上述分析可知，变压器原边电流ip起到连接谐振腔和整流电路的作用，它还包含了所有谐振变量的信息，结合公式（3）可得：

基于简化模型中推出新的等效电路如图4所示。从图可知受控电压源vn代替了原来的谐振腔和整流电路。基于假设（3），并参考文献[8]，则vn还可以写成：

然而vn与归一化频率fn之间的传递函数还是非线性的，针对这一问题，可采用泰勒级数将此方程线性化：

图4 化简后等效电路图

3 系统双闭环控制的研究

本文将在传统单回路电压控制的基础上，引入整流电流内环控制器，以改善系统动态性能，增加系统抗干扰能力，同时使系统具有快速限制谐振电流的能力[9]。控制系统结构框图如图5所示。

图5 控制策略方框图

图中kv1和kv2分别为外环电压控制器的比例参数和积分参数，ki1为内环电流控制器的比例参数。系统闭环传递函数可写为：

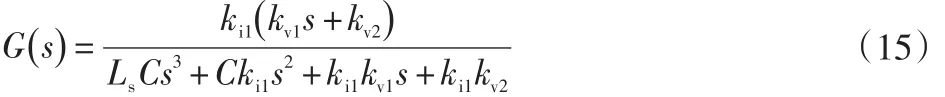
本文通过极点配置法来获取上式中的3个控制器参数[10]，假设阻尼比为ζ，固有频率为ω，则控制器参数可由以下公式获得：

式中：h通常取3～5；阻尼比ζ＞0.7；固有频率ω为500～1 000 rad/s。

4 仿真验证结果分析

为验证所提出控制方法的可行性，将使用MATLAB/Simulink仿真软件搭建全桥三电平LLC谐振变换器进行模拟仿真。在仿真模型中，利用以输出电流作为反馈电流的传统双闭环控制模型和以整流电流作为反馈电流的双闭环控制模型进行对比。为使效率达到最高，谐振变换器将工作在谐振频率，该模型的主要参数设置如表1所示。

图6所示为传统双闭环控制模型的输出电压，图7所示为新的双闭环控制模型的输出电压。从图可以看出新的双闭环控制模型有效地降低了输出电压纹波。

图6 传统双闭环控制模型输出电压波形

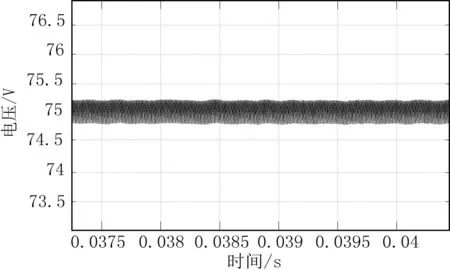
图7 新的双闭环控制模型输出电压波形

图8 所示为后级二极管电压与电流波形图，在电压上升时，电流降至为零，实现后级二级管零电流关断。

图8 整流二极管上电压及电流波形

图9 所示为开关管Q1驱动电压与开关管电压波形（为使驱动电压更加清晰，将开关管电压波形缩小25倍）。从图中可以看出当驱动电压信号Vq1到来时，开关管电压降至为0，实现前级开关管零电压开通。

图9 开关管上电压及驱动电压波形

图10 所示为每相输出端相对于点O的电压波形，从图中可以看出存在着3个电平，使每个开关管承受一半的输入电压，有效减小了开关管的电压应力。

图10 每相输出端相对于O点的电压波形

5 结束语

本文通过研究全桥三电平LLC谐振电路的工作原理，使用扩展描述函数法对电路进行建模，得出了谐振电路状态方程。由于状态方程仅仅只描述了电路的特性，并没有得到开关频率与输出电压之间的传递函数，因此控制器的设计较为困难。本文在原有状态方程的基础上进行了化简，得出了线性简化模型，并基于新的模型设计了控制器。最后用MATLAB/Simulink仿真软件进行了模拟仿真，电路前级开关管实现了零电压开通，次级整流二极管实现了零电流关断，成功降低了开关损耗，验证了控制方法的可行性。