大厚径碳纤维复合材料三维钻削有限元仿真及试验研究*

2020-05-14徐九华杨浩骏陈逸佳

金刚石与磨料磨具工程 2020年2期

张勋，陈燕，徐九华，杨浩骏，陈逸佳

(南京航空航天大学，江苏省精密与微细制造技术重点实验室，南京 210016)

碳纤维增强树脂基复合材料(CFRP)由于具有高比强度，高比模量，耐腐蚀，耐疲劳等优异性能，在新一代大型民用客机中的使用比例逐年增加。复合材料的使用比例是衡量民用飞机先进性的重要指标。在波音B787和空客A350宽体客机上，复合材料的用量分别达到了50%和52%。相比于C919 复合材料12%的用量，CR929宽体客机的复合材料用量预计会达到51%[1-4]。随着宽体客机的承力构件厚度增加，为了满足后续定位装配的需求，构件的装配孔直径随之变大，其制孔工艺面临许多难题，如加工中易造成分层、撕裂、树脂烧伤等质量问题[5]，以及刀具磨损快、成本高等问题。因此，需要对复合材料高质量制孔工艺进行优化。

目前，复合材料制孔刀具的选择及工艺参数优化主要通过工艺试验来进行，其成本高，难以预测加工过程中工件表面的应力分布、刀具各部分的载荷分布及工件出口的分层缺陷等。近年来，计算机技术及有限元仿真软件的飞速发展，使得利用有限元仿真方法来研究加工过程成为可能。与其他传统方法相比，有限元方法可以有效减少反复试验次数，降低试验成本，且正确的有限元模型可以为优化刀具结构、加工工艺参数提供理论指导。安立宝等[6-8]用ABAQUS材料库中的复合材料模型，基于二维壳单元建立CFRP钻削有限元仿真模型，并通过试验验证了有限元模型的正确性，对不同工艺参数条件下的制孔轴向力进行了预测。但该种方法仿真计算效率低，不适用于模拟大孔径厚板的钻削。PHADNIS等[9]自定义子程序，碳纤维与基体分别采用Hashin及 Puck准则判断失效，开发了用于三维实体单元建模的CFRP本构模型，建立了孔径为3 mm的单向CFRP三维钻削仿真模型。研究结果表明：该仿真模型弥补了壳单元建模的不足，能更准确地预测制孔的轴向力、扭矩和界面的分层损伤和演化；并利用验证的有限元模型对工艺参数进行了优化。ISBILIR等[10]采用复合材料宏观三维Hashin失效准则，在复合材料界面定义黏性接触，建立了直径为8 mm的单向CFRP钻削有限元模型，该模型可以预测CFRP入口处一维损伤因子的大小及钻削过程中的轴向力、扭矩。FEITO等[11]建立了孔径为8 mm的正交编织CFRP钻削有限元模型，对比了不同切削刃几何形貌的钻头对钻削轴向力及制孔质量的影响。研究结果表明：相比于工艺参数，刀具的几何形貌对制孔轴向力及工件入口分层的影响最大，该仿真结果为优化钻头几何形貌提供了参考。MAKHDUM等[12-13]构建了基于能量的线性退化碳纤维复合材料宏观力学模型，将CFRP用三维实体单元建模，建立了传统钻削及超声辅助钻削CFRP的有限元模型。研究结果表明：钻削轴向力仿真结果与试验结果有很好的匹配性，与传统钻削相比，超声辅助钻削CFRP可以明显降低钻削过程中的最大平均轴向力。

综上所述，碳纤维复合材料的钻削有限元仿真模型中复合材料的建模，从二维连续壳单元的面内损伤演化发展到自定义子程序编写的三维实体单元的连续渐进损伤，且制孔孔径大多是中小孔径。由于复合材料的多相多尺度特点[14]，大孔径厚板的三维钻削过程要基于宏观尺度，同时大孔径的三维钻削仿真钻削区域网格要细化，在相同的撒种尺度条件下，相比于中小孔区域，其网格数量大大增加。此外，渐进式损伤演化方式依赖于网格单元的特征长度，采用渐进式损伤演化方式仿真的计算时间会更长。而突变式损伤演化不依赖于单元的特征长度，仿真计算效率更高，更适合于模拟分析步时间较长的大孔径制孔过程。

由于基于突变式损伤演化的CFRP宏观尺度建模及大孔径厚板的三维钻削有限元仿真鲜有报道。因此，为了预测大孔径CFRP层合板三维钻削过程中的力载荷及出口分层缺陷，基于复合材料宏观力学，采用突变式刚度退化方式建立CFRP层合板本构模型，并在出口处嵌入Cohesive单元模拟出口的分层缺陷，最终建立大孔径CFRP三维钻削仿真有限元模型。根据相同工艺参数下的试验结果，验证有限元模型的正确性；利用验证后的有限元模型预测不同工艺参数下的钻削轴向力、出口分层缺陷，并与试验结果进行对比，计算仿真的误差范围。

1 CFRP三维钻削仿真模型的建立

1.1 CFRP本构模型

为了提高T800复合材料三维钻削仿真有限元模型的精度与可靠性，需采用三维实体单元建模，并基于ABAQUS用户中的自定义子程序接口，利用Fortran语言编写宏观等效均质单向板力学本构模型。由于CFRP三维钻削仿真过程建立的分析步是显示动力学分析的，没有建立温度位移耦合分析步，因此在本构模型中不考虑温度变化对CFRP力学性能的影响[15]。

通过ABAQUS局部坐标系分配复合材料层压板的铺层方向即可实现CFRP的铺层建模，图1为子程序执行过程流程图。

随着钻削过程的进行，材料的应力状态发生变化，材料的刚度矩阵就要进行相应的更新。为了模拟CFRP钻削过程中材料的损伤起始，需要定义CFRP损伤初始准则，因此在材料本构中纤维的失效采用Hashin失效准则，基体失效采用Puck准则。CFRP的4种失效准则如式(1)～式(4)。

图1 子程序执行流程

Hashin纤维拉伸失效准则(σ11≥0)：

(1)

Hashin纤维压缩失效准则(σ11<0)：

(2)

Puck基体拉伸失效准则(σ22+σ33≥0)：

(3)

Puck基体压缩失效准则(σ22+σ33<0)：

(4)

其中：σ11、σ22、σ12分别为材料积分点的应力分量。

仿真中用于失效准则计算判定的材料属性如表1所示，其中的X1t、X2t、X3t分别为T800在1、2、3方向上的拉伸强度，X1c、X2c、X3c分别为T800在1、2、3方向上的抗压强度，S12、S13、S23分别为12、13、23面内的剪切强度。当材料满足任意一种失效准则后，材料的损伤开始产生，材料的刚度开始退化。本文子程序中采用突变的方式进行材料的损伤演化，dft、dfc、dmt、dmc分别代表控制纤维的拉伸、纤维的压缩损伤变量及基体的拉伸、基体的压缩损伤变量，当损伤变量为1时，单元完全失效而删除，材料的刚度退化为0。仿真中用来计算刚度矩阵的T800材料力学性能参数如表2所示。

表1 平均随机一致性指标值

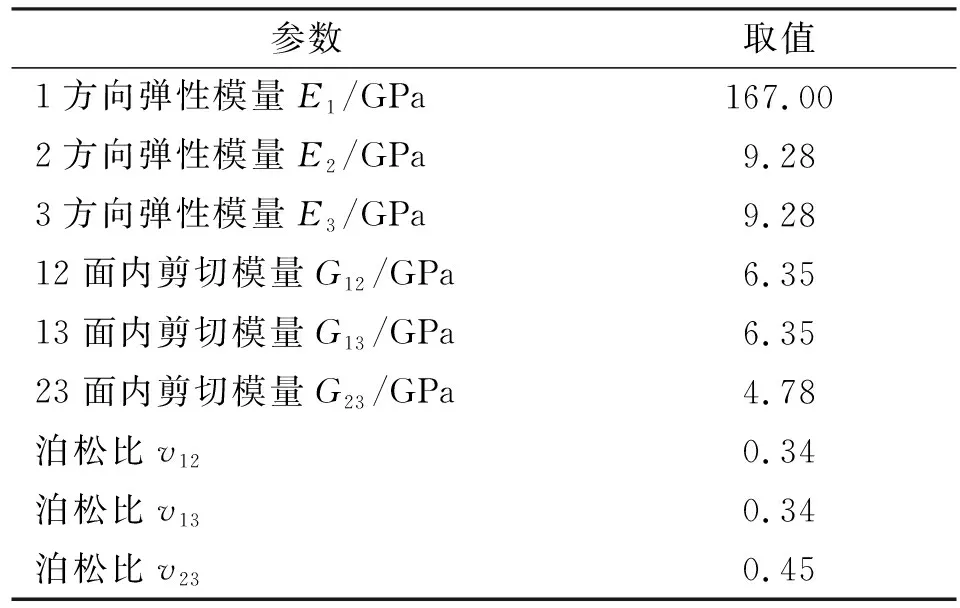
表2 T800材料力学属性

1.2 分层损伤本构模型

钻削出口处的分层损伤扩展及演化通过Cohesive单元来模拟。图2所示为Cohesive单元本构模型。

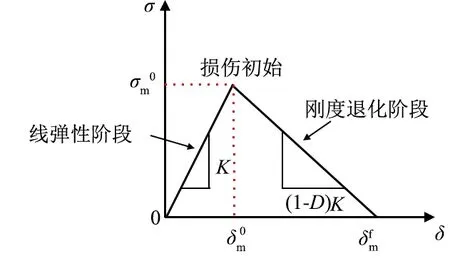
图2 Cohesive单元本构模型

Cohesive单元本构模型是基于双线性的牵引-分离响应，第一阶段的线弹性表示Cohesive单元承载阶段，第二阶段表示Cohesive单元产生损伤后的线性软化阶段。

基于Quads准则来判断Cohesive单元的初始损伤，Cohesive单元的初始损伤条件为：

(5)

当满足损伤初始条件时，Cohesive单元开始损伤并开始刚度退化，Cohesive单元的刚度退化采用线性退化方式，由损伤变量D来定义：

(6)

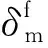
出口分层损伤的演化扩展基于能量的B-K混合模式准则来判断，基于能量的B-K混合模式损伤演化准则为：

(7)

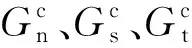
当满足B-K能量准则以后，单元完全损伤。仿真中用到的Cohesive单元材料属性如表3所示。

表3 Cohesive材料属性[9]

1.3 有限元建模流程

建立的CFRP三维钻削仿真有限元模型如图3。图3a中的刀具几何模型从UG导入，金刚石涂层刀具直径为22 mm，密度为3.52×103kg/m3，弹性模量为1.1×106MPa，泊松比为0.07；工件模型的尺寸为40 mm×40 mm×8.02 mm，其中的T800每层厚度为0.25 mm，按照[0°/90°/45°/-45°]4s的铺层顺序共32层，出口处2层的Cohesive单元厚度为10 μm。实际钻削过程中，出口分层往往发生在最后几层间，因此为了提高仿真的计算效率，仅在出口处嵌入2层黏结单元。图3b中为了模拟实际加工过程中工件与刀具的边界条件，约束了工件四周表面所有的自由度，使U1w=U2w=U3w=UR1w=UR2w=UR3w=0；钻头沿x方向与y方向的位移及角位移也被完全约束，即U1d=U2d=UR1d=UR2d=0，只对钻头施加沿z方向的进给速度及绕z轴的角速度。

(a) 铺层顺序示意图

(b) 边界条件

为了准确预测钻削载荷及出口分层，钻头及工件的网格划分质量极其重要。图3中的CFRP层合板模型被剖分成34层，每一层划分一个单元，为了在不影响仿真计算的精度同时提高计算效率，对钻头钻削的圆柱区域网格进行加密，局部撒种大小为0.5 mm，在远离钻削区域的正方形四周采用全局撒种，全局撒种大小为2 mm。采用扫掠式网格划分方式对工件进行网格划分。

CFRP材料层单元类型采用缩减积分的八节点线性六面体单元C3D8R，Cohesive层单元撒种及网格划分方式与CFRP层相同，Cohesive层单元类型为C3D8RH。为了模拟材料的去除过程，单元删除选项设置开启。为了防止网格畸变，在网格控制中均开启大变形控制，Cohesive单元的刚度退化参数设置为0.99[15]。钻头采用自由式网格划分，全局撒种大小为1 mm，在横刃及主切削刃处局部撒种加密，撒种尺寸为0.2 mm，钻头单元类型为R3D4。

在CFRP三维钻削仿真过程中，钻头与工件间存在多个接触对的接触关系，因此采用通用接触算法来定义钻削过程的接触。在通用接触设置中，每个接触对选择独立的接触属性，全局设置无摩擦。在每个独立的接触属性中，切向接触属性通过罚函数定义，法向接触属性采用硬接触。刀具与CFRP工件及Cohesive单元的接触，摩擦系数设置为0.3[16]。当Cohesive单元失效删除以后，为防止CFRP层与层间单元的侵蚀，还需定义层与层间的接触，CFRP每层间的接触摩擦系数设置为0.1[17]。且钻头通过参考点绑定为刚体。

2 钻削试验条件与方法

为了验证有限元模型的正确性，钻削试验在五轴加工中心Mikron U710机床上进行，机床的最高转速为18 000 r/min，功率为12 kW，扭矩为87 N·m，最大工作进给速度为20 m/min，最大进给加速度为7.84 m/s2。钻削过程中轴向力、扭矩通过Kistler9272测力仪采集，采集的测量信号通过5070A电荷放大器传输到PC端并进行处理，试验中所用刀具为金刚石涂层冠齿钻，刀具参数见表4。

表4 金刚石涂层刀具参数

为了防止粉尘污染机床，在CFRP入口处附近用工业吸尘器吸取加工过程产生的碎屑，钻削试验加工平台如图4所示。

图4 试验装置

试验加工参数如表5所示，每组参数做3次试验，在计算轴向力、扭矩及出口分层时取3次试验平均值与仿真结果对比。

分层损伤检测采用KSI -V400E超声波扫描显微镜检测，扫描方式采用C扫描，超声波探头工作频率为75 MHz，超声波扫描速度为0.1 m/s，待检测的制孔工件放在去离子水介质中。制孔出口的分层损伤通过分层损伤因子C来评价：

(8)

其中：Adel为制孔名义直径周围分层损伤扩展面积，Anorm为制孔孔径的名义面积。

表5 试验参数

将分层损伤检测的图像导入Matlab软件，对图像进行二值化处理得到损伤面积并计算损伤因子，同理，仿真分层损伤的面积也按上述方法处理。

3 结果与讨论

3.1 有限元仿真试验验证

为了验证大孔径碳纤维复合材料三维钻削有限元模型的正确性，准确地预测制孔过程中的轴向力、扭矩，试验对比了转速1 800 r/min、进给量0.03 mm/r、进给速度为54 mm/min时的轴向力与扭矩仿真与试验结果。图5为轴向力与扭矩仿真与试验结果对比。

从图5中可以看出：仿真与试验结果的变化趋势大致相同，大孔径碳纤维复合材料钻削过程中的轴向力及扭矩变化可分为3个阶段：第一阶段为入钻阶段，随着钻头切削刃不断钻入工件，被去除材料体积逐渐增大，轴向力及扭矩不断增大；第二阶段为稳定钻削阶段，此阶段主切削刃完全钻入工件，轴向力及扭矩达到稳定；第三阶段为钻出阶段，当钻头逐渐钻出工件时轴向力和扭矩逐渐下降，直至为零。且稳定钻削阶段的轴向力及扭矩在整个钻削过程中最大，因此选取稳定钻削阶段的轴向力、扭矩平均值进行仿真与试验结果对比分析。此时，轴向力的平均值有限元仿真结果为422.8 N，试验结果为480.4 N，扭矩平均值的有限元仿真结果为1.343 N·m，试验结果为1.659 N·m。轴向力及扭矩的仿真结果和试验结果的相对误差分别为12.0%、19.0%，证明了有限元模型预测钻削轴向力、扭矩的正确性。

(a) 轴向力仿真与试验结果对比

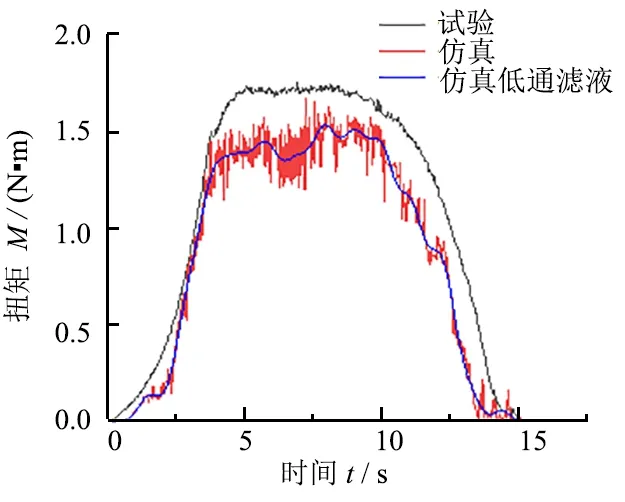
(b) 扭矩仿真与试验结果对比

图6所示为工件出口处分层损伤的仿真演化过程。图6中随着钻削的进行，钻头与工件接触面积不断增大，轴向载荷逐渐增大，当钻头逐渐钻到工件底部时，由于出口处刚度逐渐变差，CFRP开始产生分层损伤。由图6可知：钻头首先在横刃处产生损伤，发生单元失效删除，随后在横刃周围0～45°纤维切削角方向处损伤继续扩展，单元不断删除，进而分层损伤不断向四周扩展，最终呈椭圆状。

(a) 损伤开始Initial damage(b) 分层扩展Damage propagation(c) 损伤加剧Damage aggravation(d) 完全损伤Complete damage图6 出口分层损伤演化过程Fig. 6 Evolution process of exit delamination

将图6的分层损伤图像输出，导入Matlab软件计算最终的仿真分层损伤因子为1.42。而根据如图7的试验计算的分层损伤因子为1.27，仿真结果和试验结果的相对误差为 11.80%。证明了有限元模型预测出口分层的正确性。

(a) 出口分层仿真结果Simulation results of exit delamination(b) 出口分层试验结果Experimental results of exit delamination图7 出口分层仿真与试验结果对比Fig. 7 Comparison of simulation and experimental results of exit delamination

3.2 轴向力与扭矩预测分析

图8所示为转速1 800 r/min时，不同进给速度条件下，平均最大的轴向力仿真与试验结果对比。由图8可以看出：轴向力仿真结果在228.7 N至422.8 N间变化，进给速度为18 mm/min时，轴向力最小；进给速度为54 mm/min时，轴向力最大。随着进给速度的增大，轴向力不断增大，当进给速度从18 mm/min分别增大到36 mm/min和54 mm/min时，轴向力从228.7 N分别增大到346.1 N和422.8 N，即分别增大了51.3%和84.9%。此时，轴向力试验值与仿真结果的变化规律相同，轴向力试验结果在269.1 N至480.4 N间变化，仿真与试验结果相对误差在12.0%至15.0%间变化，且仿真值均比试验结果偏小。其主要原因是CFRP本构模型采用突变式刚度退化，当材料的应力状态满足失效准则时，单元即删除，单元刚度突变为零，单元失去承载能力，而实际钻削CFRP时，虽然材料产生损伤但材料并未失去承载能力，因此仿真的轴向力比试验结果偏低。

图8 轴向力预测结果对比

图9为转速1 800 r/min时，不同进给速度条件下，平均最大扭矩仿真与试验结果对比。图9和图8的结果相同，即进给速度越大，钻削CFRP的扭矩越大。扭矩的仿真结果在0.691 N·m与1.343 N·m间变化，扭矩的试验结果在0.842 N·m与1.659 N·m间变化，仿真结果与试验结果相对误差变化范围为17.9%～19.0%。同样平均最大扭矩仿真结果比实际结果小。这是由于当转速一定时，进给量增大，未变形切屑的横截面积增大，导致切削抗力增大，因此扭矩的仿真与试验结果随进给速度增大而增大。

图9 扭矩预测结果对比

3.3 出口分层预测分析

图10所示为转速1 800 r/min，不同进给速度条件下，有限元仿真预测的出口分层损伤大小与试验结果的对比。图10中随着进给速度的增大，仿真结果与试验结果均呈现上升的趋势，且有限元仿真预测结果比试验结果偏大。这是由于Cohesive单元界面刚度变化造成的。随着进给速度从18 mm/min分别增大到36 mm/min 和54 mm/min，分层因子的试验结果分别增大了4.30%和9.48%，分层因子的仿真结果分别增大了8.80%和13.60%。这是因为当转速一定时，随着每转进给量的增大，未变形切屑的横截面积增大，导致轴向力增大，当CFRP出口处层间强度一定时，轴向力越大CFRP出口越容易分层，分层损伤越大，出口分层因子也越大。有限元仿真预测结果与试验结果误差在7.76%～12.40%间变化。