基于势博弈的拥堵收费双层定价模型

刘鹏煌 （上海大学 管理学院，上海200444）

LIU Penghuang (School of Management, Shanghai University, Shanghai 200444, China)

0 引 言

随着城镇化进程不断加快和汽车工业快速发展，我国许多城市面临严重的交通拥堵问题，缓解交通拥堵刻不容缓。交通拥堵的原因主要有道路基础设施不足，私家车数量急剧增加和出行者出行决策低效。道路基础设施不足和私家车数量急剧增加都是刚性约束，在未来一段时间内还难以彻底改变，而出行者出行决策低效更易于改变。出行者出行决策低效主要体现在：出行者在选择出行路径时，相互争夺出行成本较低的路径，忽略自身决策对路网环境的影响；此外，出行者在选择出行方式时放弃容量大的公交车而选择更舒适的私家车，出行者低效的出行决策降低路网资源利用率，如果能够通过某种方式改变出行者低效出行决策，提高路网资源利用率，就能有效缓解城市交通拥堵。

道路拥堵收费在提高出行者出行效率，缓解城市交通拥堵上卓有成效，目前已在伦敦、新加坡、斯德哥尔摩等城市成功实施，其本质是一种交通需求管理的经济手段，目的是利用价格机制限制繁忙时段和繁忙路段上的车流密度，提高路网资源利用率。拥堵收费的难点在于拥堵收费定价，目前构建拥堵收费定价的方法主要有边际定价法、瓶颈模型法和双层规划法。关于边际定价法，Walter[1]首次定量研究道路拥挤的外部效应，提出短期边际成本定价模型，确定传统拥挤定价理论；Dafermos[2-3]将边际成本定价理论应用于确定路网中不同等级用户的收费模式，并将路段收费和路径收费的问题公式化。关于瓶颈模型法，Vickrey[4]应用确定性排队理论提出道路拥堵收费单通道瓶颈模型，该模型论述排队拥挤的消涨过程和用户的时间决策，用动态过程分析道路拥堵状况，给出基于时间的拥堵收费定价方案；Henderson[5]在道路瓶颈模型中考虑计划时间延误和出行者出发时间决策，给出从道路流量出发的动态拥堵收费定价方法；吴子啸和吴海军[6]对Vickrey 提出的瓶颈模型进行改进，将出行需求由固定值改为弹性需求，将出行者特征由相同改为有差异，得到一个新的拥堵收费定价模型；卢晓珊等[7]基于瓶颈理论构建出行成本均衡的分层拥堵收费定价模型，讨论不同机制下地铁票价和停车收费策略。关于双层规划法，Yang 和Lam[8]认为双层规划模型是最佳的拥堵收费定价模型，并利用双层规划法对道路拥堵收费进行研究；Yang 和Bell[9]将次优分析的思想应用于双层规划，提出基于双层规划的次优收费方法，并采用基于灵敏度分析的算法进行求解；李志纯等[11]建立弹性需求下以用户盈余最大化为上层目标的道路拥堵双层规划模型，下层模型为弹性需求下的随机用户平衡，并利用惩罚函数法和步长加速法相结合的算法框架求解；姚红云等[12]考虑异质出行者的影响，以时间价值不同对用户特性进行分类，得到弹性需求下多类型用户的拥堵收费模型。从现有的拥堵收费定价模型来看，边际定价法未考虑时间、空间和交通量的变化，即路网在任意时间均处于稳定状态，交通需求和出行成本不随时间变化而变化；瓶颈模型法太过理想化，它把道路瓶颈的容量描述为一个连续的出行时间函数，并且是部分线性的，甚至将排队过程纳入静态问题的范畴；双层规划法最贴近实际情况，它同时优化交通管理者与出行者的决策，但双层规划模型太复杂，不易求解。本文拟采用双层规划法构建拥堵收费定价模型，由于双层规划不易求解，考虑运用势博弈将双层规划转化成单层规划，在保证拥堵收费定价模型贴近实际情况的同时，降低双层规划求解难度。

拥堵收费能否顺利实施依赖公众对该策略的支持，虽然拥堵收费能够有效缓解城市交通拥堵，但该策略由于其收入的不透明和不公平仍然没有被公众所接受，为了克服该缺陷，提高公众对该策略的支持程度，很多学者对拥堵收费及其返还政策进行研究。Goodwin[13]提出将道路拥堵收入三等分，分别分给政府、快轨和城市道路基础设施建设及公交系统；Mireabel 和Rrymond[14]提出将拥堵收费收入重新分配给地铁系统，并得到使拥堵收费政策更有效率的地铁票价；姜沂兵等[15]应用累积前景理论分析用户出行行为，建立拥堵收费及其返还的优化模型，得到不同需求分布下的最优收费和最优票价折扣费率。针对拥堵收费的不公平性问题，本文拟将拥堵收费与公交系统联系起来，考虑将拥堵收费收入以公交票价打折的形式补贴出行者，如此既可以提高公众对拥堵收费的支持程度，又能鼓励出行者选择公交车出行。

1 符号说明与模型假设

本文研究的路网由节点、路段和路径组成，分别对应网络图中的点、边和链。路网的决策者有出行者和交通管理者，首先考虑出行者与交通管理者的决策。出行者根据交通管理者给出的路段拥堵收费和路网补贴率选择出行成本最低的路径出行；反过来，交通管理者根据路段的出行者数量决定路段拥堵收费和路网补贴率，目标是最小化路网总出行成本。出行者与交通管理者的决策相互影响构成一个双层规划模型。其次考虑出行者之间的决策，出行者根据其他出行者的决策选择出行路径，只要出行者发现路网中有更低出行成本的路径，就会改变自身的策略，而出行者的策略变化又会影响其他出行者的决策，出行者之间的决策相互影响构成一个非合作博弈。综上，本文研究的问题可描述为一个双层规划模型，上层为交通管理者的决策模型，其目标是最小化路网的总出行成本，下层为出行者非合作博弈模型，每个博弈方最小化自身的出行成本。

1.1 符号说明

A为路网中路段的集合，A=｛1,2 ,…,a｝；R为路网中路径的集合，R= ｛1,2 ,…,r｝；W为路网中OD对的集合，W= ｛1,2 ,…,w｝；M为路网中出行者类型的集合，M= ｛1,2 ,…,m｝；Rw为OD对w间的路径的集合；Bm为第m类出行者对私家车的偏好程度；Va为路段a的出行者数量；对w间第m类出行者的数量；τa为路段a的拥堵收费；γ 为拥堵收费上限；θa为路段a的道路容量；为路段a上的自由流出行时间；β 为出行时间与出行量的相关系数，β 为常数，且β∈［0,1 ］；ta为路段a的出行时间；λ 为出行者单位出行时间的成本，且λ∈［0,+ ∞ ］；为0-1 变量，当路径r通过路段a时为1，否则为0；μ 为公交补贴率，即公交票价减免的比例；εa为路段a的公交票价；为第m类出行者选择路径r的出行者数量；Pm为第m类出行者的策略，为非合作博弈的策略集，为第m类出行者选择私家车出行时路段a的出行成本；为第m类出行者选择公交车出行时路段a的出行成本为第m类出行者选择路径r的广义出行成本；Um为第m类出行者的总出行成本；U为路网的总出行成本。

1.2 模型假设

假设1 假设出行者的出行方式只有公交车和私家车两种，且出行者没有固定的出行方式，具体选择哪一种出行方式取决于出行者对公交车和私家车的偏好程度，出行者对哪种出行方式的偏好程度越大，选择该出行方式出行的机率就越大。

假设2 假设路网中出行者不同时间的出行决策是在同一时间进行的，若以天为时间单位，则路径的出行量等于当天选择该路径的出行者数量。

假设3 假设路网中的出行者均为日常上下班通勤的出行者，故认为出行者有自己固定的交通起止点，即OD对。假设4 假设路段的出行时间与出行量正线性相关，路段a的出行时间为其中Va为路段a的出行量为路段a的自由流出行时间，即车辆在不拥堵情况下正常驾驶消耗的时间，假设路网中所有出行者的单位出行时间成本相同。假设6 假设同种类型的出行者出行策略相同，即选择各路径的概率相等。

假设7 假设出行者是完全信息和完全理性的，即出行者能够准确获取路网上的信息，包括路段的出行时间、拥堵收费和路网的公交补贴率，且出行者总是选择出行成本最低的路径。

假设8 假设交通管理者只对私家车出行者收取拥堵收费，并以票价打折的形式补贴公交车出行者，交通管理者收取拥堵收费主要根据道路的剩余容量，不妨设路段a的拥堵收费。

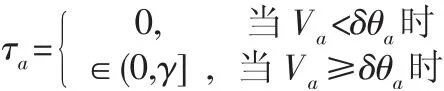
其中：θa为路段a的道路容量，γ 为拥堵收费的上限，δ 为比例系数，即一定比例的道路容量，δ 为常数，且

2 模型建立与分析

2.1 出行成本函数

本节拟构建第m类出行者的总出行成本函数和路网总出行成本函数。

引理1 路网中第m类出行者的总出行成本为：

路网的总出行成本为：

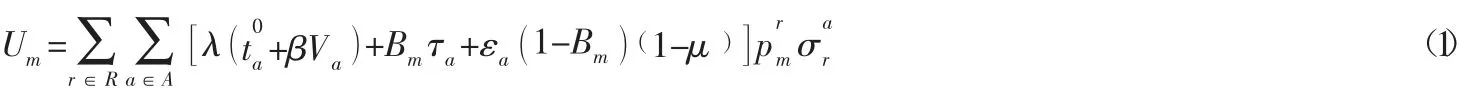
证明：按照出行者对公交车和私家车的偏好程度对出行者划分，用表示第m类出行者对私家车的偏好程度，则1-Bm表示第m类出行者对公交车的偏好程度。又 表示第m类出行者选择路径r的数量，根据假设2 可得路径r的出行量为：

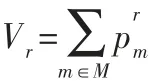
而路段出行量为通过该路段所有路径的出行量的总和，故路段a的出行量为：

当出行者选择私家车出行时，出行成本由时间成本和拥堵收费组成，根据假设4 可得第m类出行者选择私家车出行时，路段a的出行成本为：

当出行者选择公交车出行时，出行成本由时间成本和公交票价组成，其中公交票价为补贴后的公交票价，故第m类出行者选择公交车出行时，路段a的出行成本为：

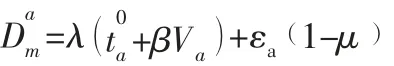
由假设1 可知出行者没有固定的出行方式，因此用公交车出行成本和私家车出行成本的加权和表示出行者的广义出行成本，路径的广义出行成本为该路径所有路段广义出行成本的总和，故第m类出行者选择路径r的广义出行成本为：

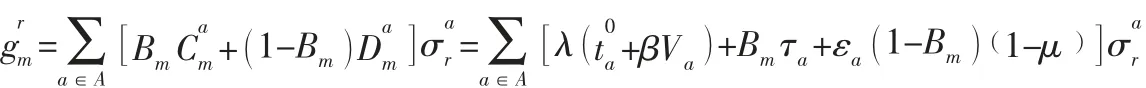
第m类出行者的总出行成本为所有路径上第m类出行者出行成本的总和，故第m类出行者的总出行成本为：

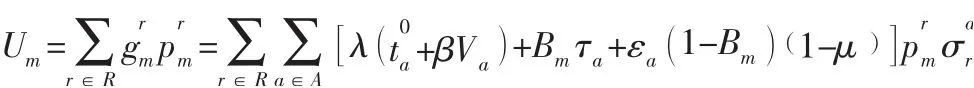
路网的总出行成本为所有类型出行者出行成本的总和，故路网的总出行成本为：

2.2 非合作博弈模型

本节拟构建出行者非合作博弈模型，由假设6 可知同类型的出行者选择各路径出行的概率相等，因此将路网中同类型的出行者视为一个博弈方，故路网中有多少种类型的出行者就对应多少个博弈方，博弈方m的策略为非合作博弈的策略集为P=P1×P2×…×Pm，博弈方m的支付函数为第m类出行者的总出行成本，则非合作博弈模型可描述为G

引理2 博弈G是一个精确势博弈，且势函数为：

证明：将式（3） 代入式（1） 得：

令：

则：

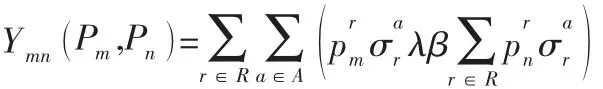
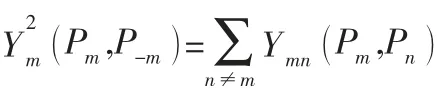
引理1 证明博弈G为精确势博弈，根据精确势博弈的性质，博弈G至少存在一个纯策略Nash均衡，博弈G的Nash均衡策略满足：

其中：P-m为除博弈方m外的博弈方策略，为博弈方m改变策略后的策略。

2.3 双层规划模型

在制定路段拥堵收费和公交补贴率时，交通管理者的目的最小化路网的总出行成本，当交通管理者给出每条路段的拥堵收费和公交补贴率后，各类出行者之间进行非合作博弈，各类出行者不断调整自身的策略，最终得到Nash均衡，交通管理者根据Nash均衡策略调整路段拥堵收费和公交补贴率，直到非合作博弈Nash均衡条件下，路网的总出行成本最低，故可将式（4）作为交通管理者决策模型的约束，得到双层规划模型：

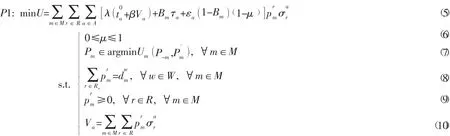
其中：式（5） 为交通管理者的目标函数，即最小化路网的总出行成本；式（6） 为公交补贴率的取值范围；式（7） 为博弈G的Nash均衡条件；式（8） 为出行者的出行需求约束，即第m类出行者分配到OD对w间的出行者总数应等于第m类出行者在OD对w之间的总出行需求；式（9） 为第m类出行者选择路径r出行数量的取值范围；式（10） 为路段a上的出行者数量。

2.4 双层规划模型转换

由式（7） 可知，下层博弈G为多目标规划，即所有博弈方的支付函数最小，这样的特征使得P1 非常复杂，用现有方法很难直接求解。本文拟利用Nash均衡的定义，将博弈G转换为若干个约束，利用这些约束限制博弈G的策略空间，进而将P1转换为单层规划。

对于每一个博弈方，其单方面的策略改变称为策略偏差，本文用r维的向量表示博弈方m的策略偏差，其中为博弈方m在路径r上的出行量变化。由于博弈方m的出行者总数不发生改变，即某条路径上博弈方m的出行者数量增加，必有其它路径上博弈方m的出行者数量减少，因而博弈方m的出行者数量变化满足：

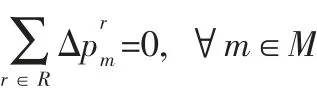
此外，路径r上博弈方m的出行者数量变化满足：

当博弈方m的策略从Pm变化为Pm+ΔPm时，支付函数的变化为：

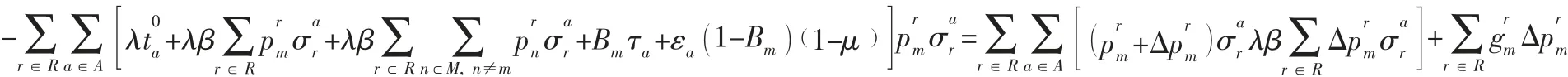
在Nash 均衡条件下，没有哪个博弈方能够通过策略偏差来降低自身的出行成本，因此出行成本变化满足：

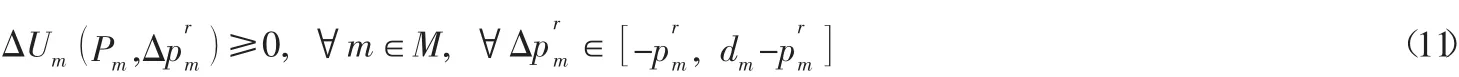
用式（11） 替换式（7） 得到下面的单层规划模型：

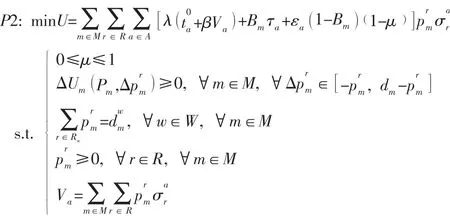
从式（11） 可以看出，变量的取值非常多，包括整数变量和连续变量，且整数变量的取值范围非常大，处理比较困难，需要对式（11） 进一步简化。本文考虑一种更简单的策略变化，即简单策略偏差，利用简单策略偏差缩小整数变量的取值范围。

简单策略偏差是指博弈方只改变一对纯策略的概率，其它纯策略的概率保持不变。同样用r维向量表示博弈方m的简单策略偏差，博弈方m只改变纯策略x和y的概率。令同理可得简单策略偏差情况下，博弈方m的支付函数变化为：

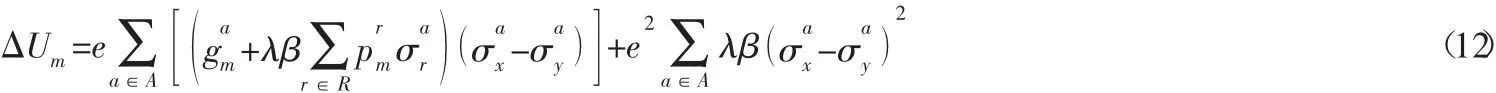
在Nash均衡条件下博弈方m的支付函数变化满足由式（12） 可知ΔUm是关于e的一元二次函数，且开口向上，令ΔUm=0，可得：内成立，即满足Nash均衡条件，必须要求e2＜0，故博弈G的Nash均衡条件为：

为保证

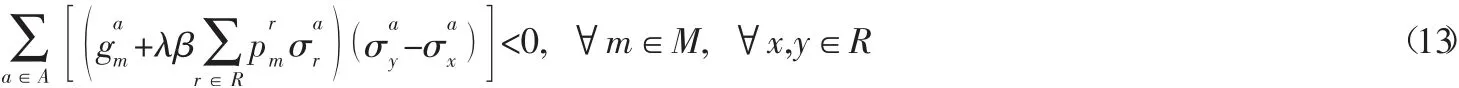
用式（13） 替换式（11），得到下面的单层规划模型：

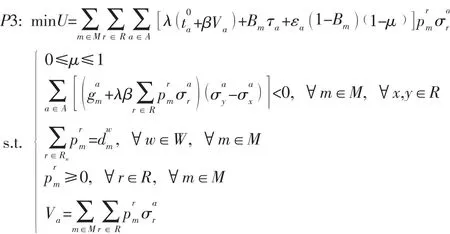
2.5 出行决策效率分析

Price of anarchy（POA） 是博弈论中的一个重要概念，字面意思是博弈方由于自私自利行为导致的效率损失，具体来讲，它是度量博弈方分布式自私行为与Pareto最优的效率偏差，定义为博弈方非合作博弈的总支付函数值与合作博弈的总目标函数值之比。

在非合作博弈情形下，每一个博弈方最小化自身的支付函数：

在合作博弈情形下，每一个博弈方最小化博弈方的总支付函数：

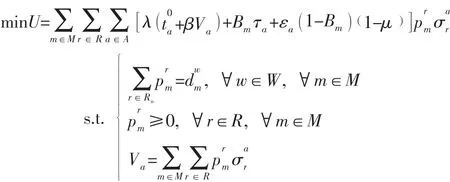
由式（14） 可知，对于交通管理者给出的τa和μ，POA的值越小，博弈方的总出行成本越接近Pareto最优，出行者的出行决策越高效，反之，出行者的出行决策越低效。

3 算例分析

通过一个具体的算例对单层规划模型P3 进行分析，考虑如图1所示的路网有4 个OD对：

路网中包含四种类型的出行者，各类出行者的数量均为230，各类出行者对私家车的偏好程度分别为：B1=0.2，B2=0.4，B3=0.6，B4=0.8。各OD对之间各类出行者的数量如表1 所示：

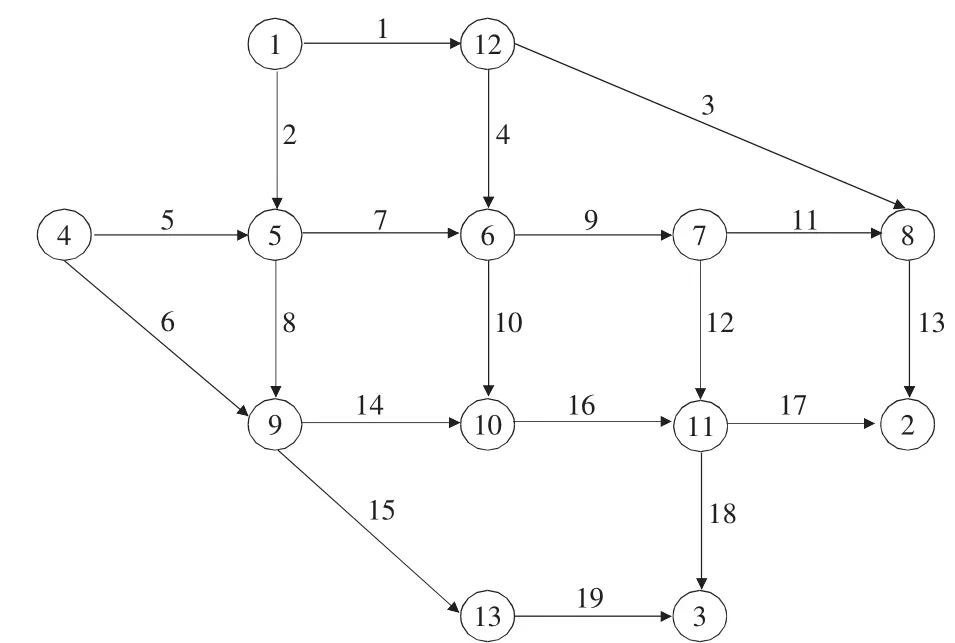
图1 路网示意图

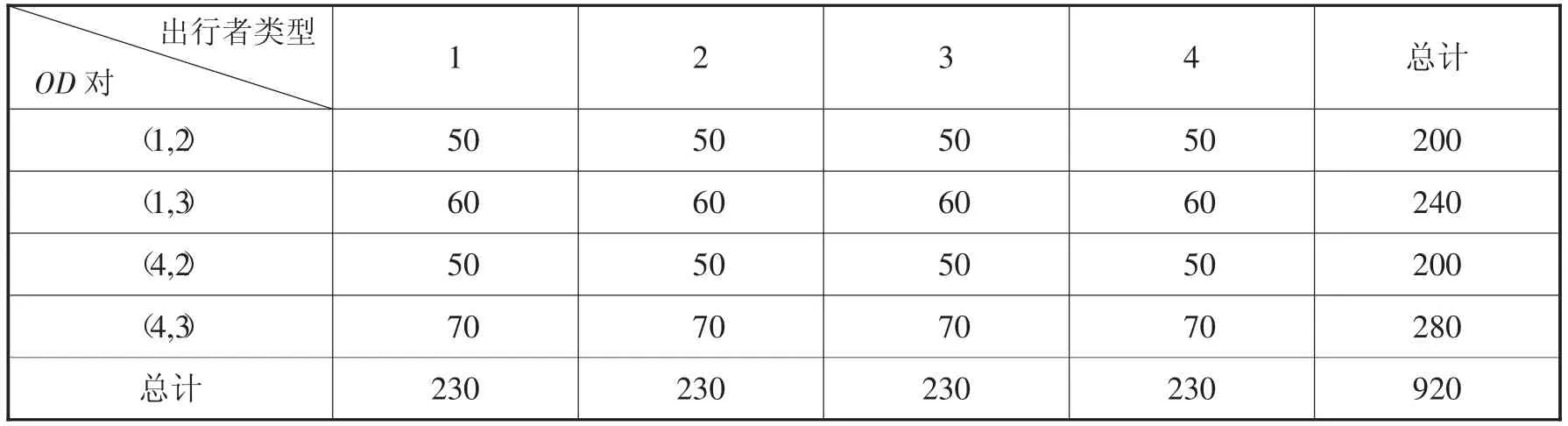
表1 OD 对之间各类出行者的数量

基于上述参数，通过Matlab7.0 软件在无收费无补贴、有收费无补贴、有收费有补贴三种情形下，计算各类出行者的出行成本、路网的总出行成本和POA值。三种情形下各类出行者的出行成本如图2 所示，横坐标表示交通管理者的策略类型，纵坐标为各类出行者的出行成本。

从图2 可以看出，从无收费无补贴，到有收费无补贴，再到有收费有补贴，各类出行者的出行成本逐次降低，这说明拥堵收费和公交补贴均能有效降低各类出行者的出行成本。比较出行成本的下降幅度可知，有收费有补贴的出行成本下降幅度最大，有收费无补贴次之，这说明拥堵收费和公交补贴同时实施的效果优于仅拥堵收费。

三种情形下，路网的总出行成本如图3 所示，横坐标表示交通管理者的策略类型，纵坐标表示合作与非合作两种情形下路网的总出行成本。

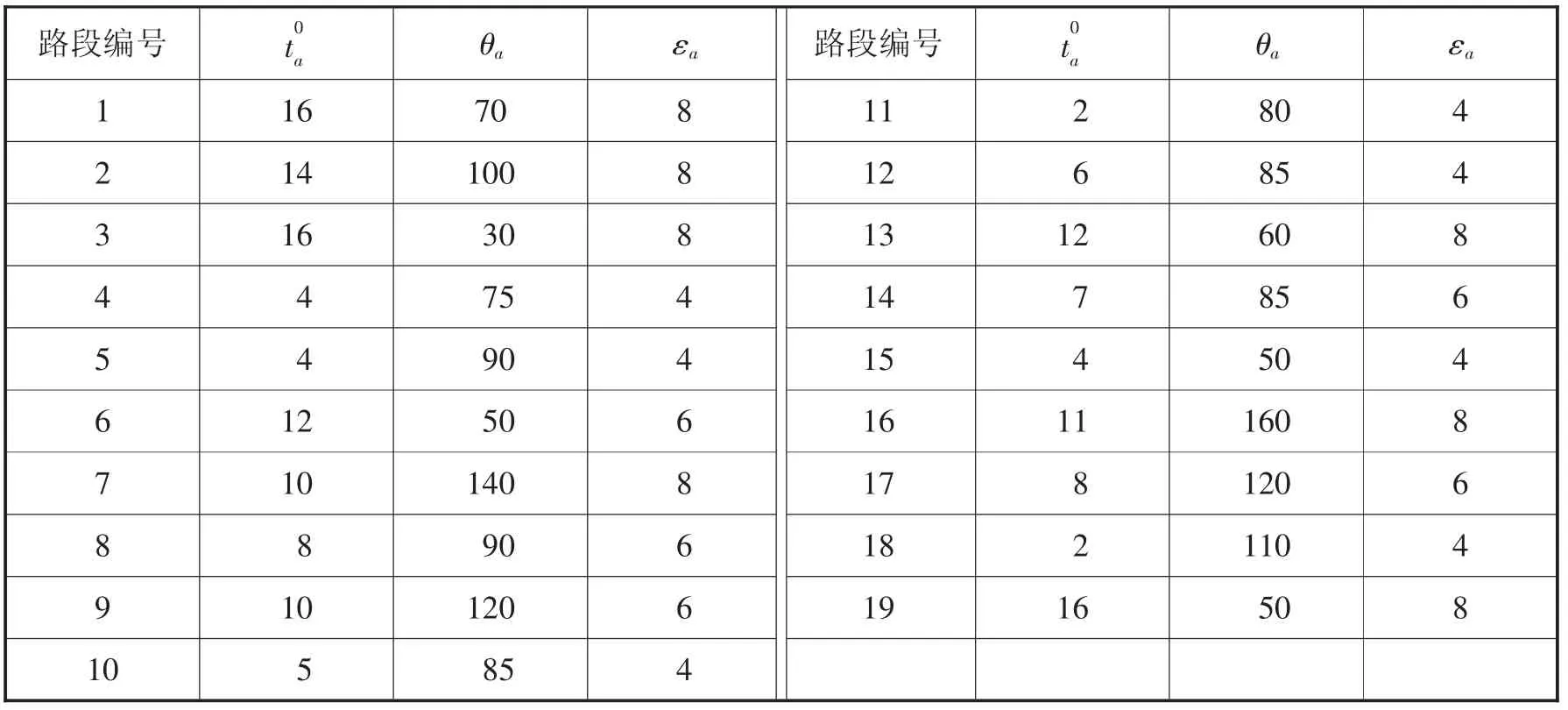
表2 路段参数

图2 三种情形下各类出行者的出行成本

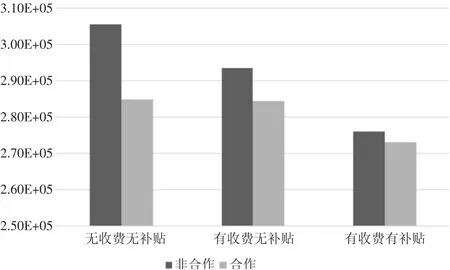
图3 三种情形下路网的总出行成本

从图3 可以看出，从无收费无补贴，到有收费无补贴，再到有收费有补贴，合作与非合作的路网总出行成本均逐次降低，这与图2 得到的结果一致。比较出行者合作与非合作两种情形下路网总出行成本可知，合作的路网总出行成本总是低于非合作的路网总出行成本。此外，有收费有补贴出行者合作与非合作的路网总出行成本差值最小，这说明拥堵收费和公交补贴均能减少出行者因利益博弈造成的损失，且拥堵收费和公交补贴同时实施时效果最佳。

三种情形下POA值如图4 所示，横坐标表示交通管理者的策略类型，纵坐标为相应的POA值。

从图4 可以看出，三种情形下POA值均大于1，即非合作的路网总出行成本总是高于合作的路网总出行成本，这说明非合作得到的是低效率的Nash均衡，而合作博弈得到的是高效率的Pareto最优。比较三种情形下的POA值，从无收费无补贴，到有收费无补贴，再到有收费有补贴，POA的值逐次降低，这说明有收费有补贴时出行者的出行决策最高效，有收费无补贴其次，无收费无补贴最低。

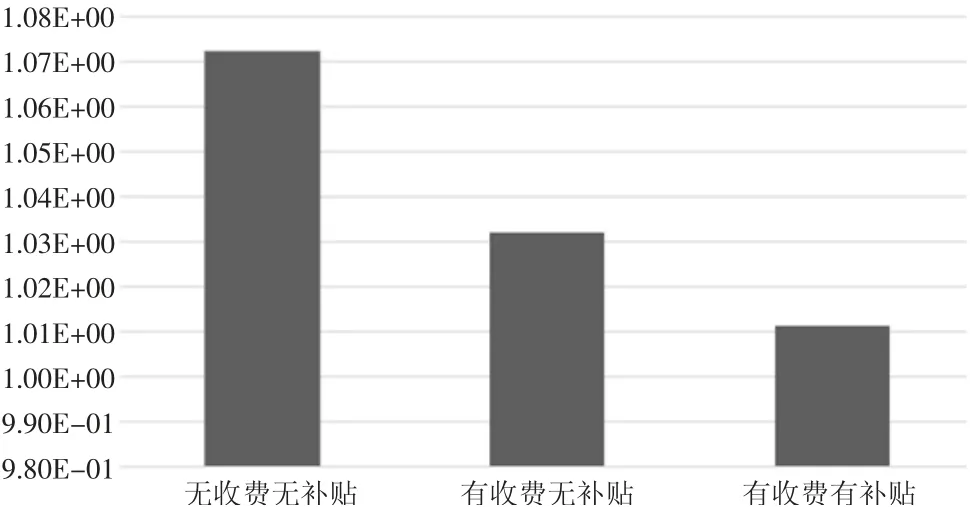
图4 三种情形的POA 值

4 结 论

本文同时考虑拥堵收费和公交补贴，采用双层规划与博弈论结合的方法，构建拥堵收费定价模型，上层为交通管理者的决策模型，下层为出行者非合作博弈模型。利用势博弈理论证明下层非合作博弈为势博弈，从而下层非合作博弈存在Nash均衡。基于博弈方的策略偏差将双层规划模型转换为易于处理的单层规划。最后，通过具体的算例在不收费不补贴、有收费无补贴、有收费有补贴三种情形下，计算各类出行者的出行成本、路网总出行成本和POA值，结果表明：拥堵收费和公交补贴均能有效降低各类出行者的出行成本和路网总出行成本，使出行者的出行决策更高效，且拥堵收费和公交补贴同时实施的效果最优。