HUIM-IPSO:一个改进的粒子群优化高效用项集挖掘算法
2020-05-14王常武尹松林刘文远魏小梅郑红军杨继萍
王常武,尹松林,刘文远,魏小梅,郑红军,杨继萍
1(燕山大学 信息科学与工程学院,河北 秦皇岛 066004)
2(北京联合大学 机器人学院,北京 100101)
E-mail:wcw@ysu.edu.cn
1 引 言
频繁项集挖掘(Frequent Itemset Minging,FIM)的任务是挖掘出事务数据库中的频繁项集[1],即挖掘出交易数据库中频繁出现的项目组合.频繁项集挖掘是许多应用的基础,其中最经典的应用是购物篮分析问题[2].人们对频繁项集挖掘已经做了很多工作,频繁项集挖掘需要满足两个假设:1)每个项目在每次交易中不会出现多次;2)所有项目具有相同的重要性(单位利润或价值).在实际生活中,这两个假设却经常得不到满足.例如考虑客户交易数据库,客户通常会购买同一商品的几个单位(例如,客户可能会购买几瓶果汁),并且商品具有各不相同的单位利润(例如,销售钻石比销售一瓶果汁产生更多的利润).频繁项集挖掘算法不能同时考虑到商品的购买数量和单位利润,只能找到频繁出现的商品组合,而不是那些能够产生高利润的商品组合[3].
考虑到购买数量和单位利润,人们进一步提出了高效用项集挖掘(High Utility Itemset Mining,HUIM)[4].高效用项集挖掘的目标是发现具有高效用(例如,高利润)的项集,即高效用项集(High Utility Itemset,HUI).高效用项集的传统挖掘算法都会面临项集的搜索空间呈“指数增长”的趋势[5].
生物启发计算能通过迭代不断改进候选解决方案,从而优化问题.2014年,Kannimuthu和Premalatha提出了基于遗传算法(Genetic Algorithm,GA)的高效用项集挖掘算法—HUPE-GARM算法[6,7].由于每一次迭代中随机选择和变异生成的新项集会明显不同于上一代的结果,算法的收敛速度会很慢.因此HUPE-GARM算法在一定的迭代次数中只能挖掘出少量的高效用项集.2017年,Lin等人提出了一种基于粒子群优化(Particle Swarm Optimization,PSO)的高效用项集挖掘算法—HUIM-BPSO算法[8,9].高效用项集挖掘问题不同于只有少量最优值的问题,它需要挖掘出所有效用值不小于效用阈值的项集.由于高效用项集在数据集中的分布是不均匀的,粒子群优化算法将上一代种群的最优值作为下一代种群的优化值进行搜索可能会导致在一定次数的迭代次数中遗漏一些高效用项集.
本文提出了一个改进的粒子群优化(Improved Particle Swarm Optimization,IPSO) HUIM-IPSO算法.算法(1)通过轮盘赌选择法在当前代种群的高效用项集中,以一定概率选择下一代种群的优化值,增加了种群的多样性;(2)使用位图矩阵来表示事务数据库和非期望编码向量修剪策略去除事务数据库中不存在的项集,加快了算法挖掘高效用项集的速度.实验结果显示,HUIM-IPSO算法比HUPE-GRAM算法和HUIM-BPSO算法有更高的挖掘效率和更快的收敛速度.
2 高效用项集挖掘和粒子群优化
2.1 高效用项集挖掘
令I={i1,i2,…,in}是一个有限的项目集合.事务数据库DB由1个事务表和1个外部效用表构成.事务表由多个事务{T1,T2,…,Tn}构成,其中每个事务Tc⊆I,同时每一个事务Tc都有唯一的标识符Tid.外部效用表则保存了每个项目的单位利润或者重要度.
定义1.由若干个项目构成的一个集合,称为项集.包含k个项目的集合一般称为k-项集.
定义2.对于每个事务Tc中的每个项目i∈Tc都会对应一个表示项目购买数量或者出现频次的正整数iu(i,Tc),称为项目的内部效用.每个项目还会对应一个表示单位利润或者重要度的正整数eu(i),称为项目的外部效用.
表1和表2给出了一个事务数据库示例.数据库包含10条互不相同的事务(T1,T2,…,T10).在事务T2中包含项目(b,d,e,f),项目对应的内部效用值分别为(6,1,1,1).其中,事务T2中项目b对应的内部效用为6,表示事务T2中b出现了6次.从表2可得,事务T2中这些项目的外部效用为(9,5,6,1),其中项目b对应的外部效用为9,表示项目b的重要度为9.
定义3.在事务中项目的外部效用与内部效用的乘积,称为项目效用.记为u(i,Tc),如式(1)所示.
u(i,Tc)=eu(i)×iu(i,Tc)
(1)
式中,i表示事务Tc中的项目;eu(i)表示项目i的外部效用;iu(i,Tc)表示事务Tc中项目i的内部效用.
由定义3容易得到事务Tc中项集X的效用如式(2)所示.
u(X,Tc)=∑i∈X∧X⊆Tcu(i,Tc)
(2)
它表示项集X中每个项目i的效用加和.
例如在表1和表2的示例中,事务数据库中事务T2中项目b的效用为u(b,T2)=6×9=54.在事务T2中项集{b,e}的效用为u({b,e},T2)=u(b,T2)+u(e,T2)=54+6=60.
定义4.在事务数据库中项集的总效用,称为项集总效用.记为u(X),如式(3)所示.
u(X)=∑Tc∈DBu(X,Tc)
(3)
式中,X表示事务Tc中的项集.
例如在表1和表2的示例中,事务数据库中项集{a,c}的总效用u({a,c})=u({a,c},T1)+u({a,c},T3)+u({a,c},T8)=21+7+34=62.
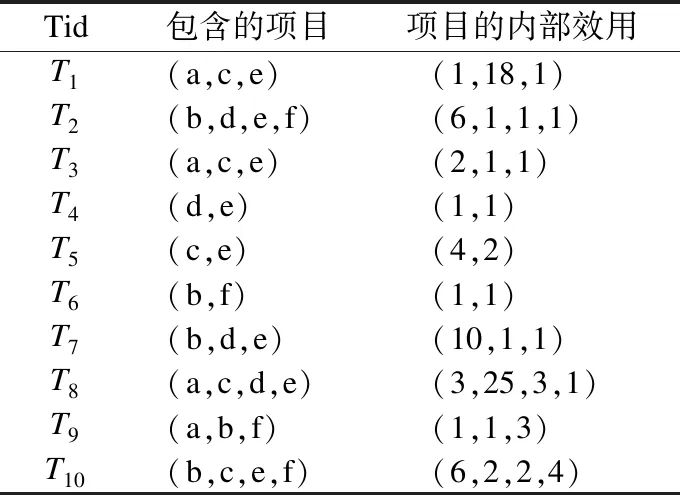
表1 事务信息

表2 项目的外部效用
定义5.在事务数据库中项集总效用大于等于效用阈值的项集,称为高效用项集.记为HUI,如式(4)所示.
HUI={X|u(X)≥minutil}
(4)
式中,minutil表示效用阈值.
例如在表1和表2的示例中,如果minutil= 115.项集{b,f},{b,e,f},{b,d},{b,d,e},{b},{b,e}都是高效用项集,它们的效用分别为135,131,154,166,216和222.
能够证明项集的效用既不是单调的,也不是反单调的.由此可知,一个项集可能有低效用的、相等效用的或者高效用的子集[10].因此,在频繁项集挖掘问题中使用的修剪项集搜索空间的方法,在高效用项集挖掘问题中不能直接使用.
为了解决项集效用值既不是单调的,又不是反单调的这个问题,一些高效用项集挖掘算法中提出了事务加权效用,而它是反单调的[11].
定义6.事务数据库中事务的效用,称为事务效用.记为TU(Tc),如式(5)所示.
TU(Tc)=∑i∈Tcu(i,Tc)
(5)
式中,u(i,Tc)表示在事务Tc中项目i的项目效用.
表3给出了事务T1,T2,…,T10的事务效用.

表3 事务效用
定义7.事务数据库中,经常会出现多个事务包含某个项集,这些事务的效用加和称为某项集的事务加权效用.记为TWU(X),如式(6)所示.
TWU(X)=∑Tc∈DB∧X⊆TcTU(Tc)
(6)
定义8.设项集X,如果TWU(X)≥minutil,则X称为高事务加权效用项集,记为HTWUI;反之,称X为低事务加权效用项集,记为LTWUI,如式(7)和式(8)所示.
HTWUI={X|TWU(X)≥minutil}
(7)
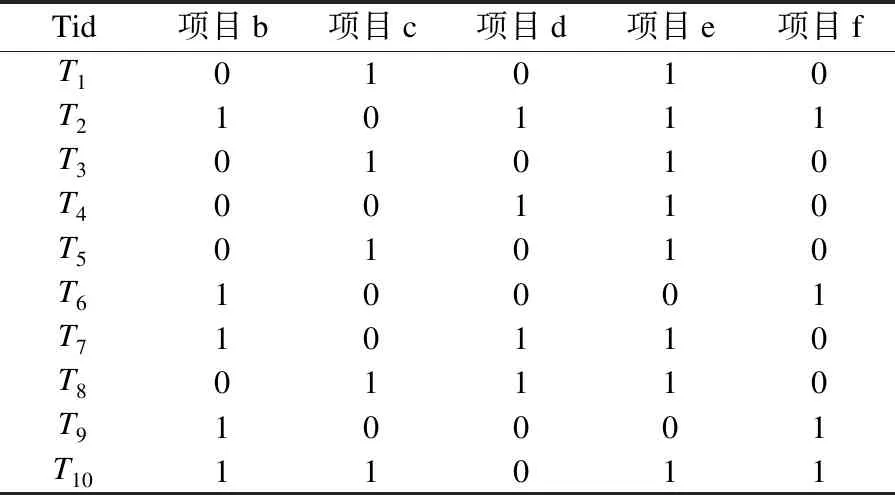
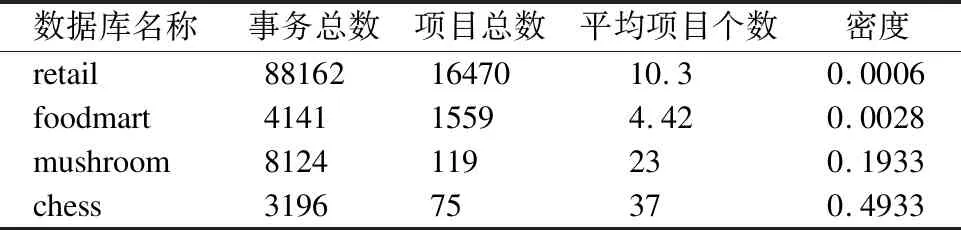
LTWUI={X|TWU(X) (8) 式中,minutil表示效用阈值.包含k个项目的HTWUI和LTWUI分别记为k-HTWUI和k-LTWUI. 事务加权效用具有3个重要的性质. 性质1.令项集X,则有TWU(X) ≥u(X),说明项集的事务加权效用是它本身效用值的向上估计. 性质2.设项集X、Y,如果X⊆Y,那么有TWU(X)≥TWU(Y).这说明事物加权效用是反单调的. 根据定义2,性质1和性质2是显然成立的. 性质3.设项集X,如果TWU(X) 性质3可以使用性质1和性质2进行证明,同时该性质在高效用项集挖掘算法中经常被用来修剪项集的搜索空间. 1995年,Eberhart和Kennedy提出了粒子群优化算法. 粒子群优化采用公式(9)和公式(10)对粒子的位置进行更新. (9) (10) 式中,i= 1,2,…,m;w是大于等于0的数,称为惯性因子;加速常数c1和c2也是大于等于0的数;r1和r2是范围在[0,1]内的随机数. 迭代终止的条件根据具体问题设定,一般是迭代次数达到预定的最大值或者是粒子群优化所能够搜索到的最优值满足了目标函数的最小容许误差. 基于粒子群优化的高效用项集挖掘算法中,项集用来表示粒子,项集总效用用来表示适应值.然后选择一个合适的迭代次数就可以进行高效用项集的挖掘了. 算法输入为效用阈值和需要挖掘的事务数据库.用位图矩阵表示事务数据库.通过轮盘赌选择法和非期望编码向量修剪策略初始化种群.粒子适应值通过公式(3)计算,保留适应值不小于效用阈值的粒子作为高效用项集.通过轮盘赌选择法在当前代种群的高效用项集中选择下一代种群的初始优化值.当前代种群中第i个高效用项集被选中的概率记为Si,如公式(11)所示. (11) 式中,SHUI表示当前代种群中所有高效用项集的集合,|SHUI|表示集合SHUI中元素的数量,fitnessi表示发现的第i个高效用项集的适应值.通过粒子位置更新公式(9)和公式(10)以及非期望编码向量修剪策略生成下一代种群.每次迭代中都有适应值的计算、高效用项集的识别和下一代种群的生成,直到达到最大迭代次数. 3.2.1 位图表示法 定义9.设Veci和Vecj是两个长度为len的编码向量,编码向量是由0或1构成的向量,则这两个向量中具有不同值的位置集合,称为编码向量的异位集.记为BitDiff(Veci,Vecj),如公式(12)所示. BitDiff(Veci,Vecj)= {num|1≤num≤len,bnum(Veci)⊕bnum(Vecj)=1} (12) 式中,bnum(Veci)表示Veci第num个位置的值;⊕表示异或运算. 定义10.将事务数据库表示成矩阵的形式称为事务数据库的位图矩阵.已知DB={T1,T2,…,TN}是一个事务数据库,M为事务数据库DB中项目的总数,则DB的位图矩阵记为B(DB).B(DB)是一个N×M的布尔型矩阵,其中B(DB)中每一个元素要么是1,要么是0.B(DB)第j行、第k列元素表示事务Tj是否包含项目ik,如公式(13)所示. (13) 在公式(13)中,如果项目ik在事务Tj中,那么DB中第j行,第k列为1.否则,该位置的元素为0. 定义11.位图矩阵中包含指定项目的某一列称为该项目的位图覆盖.位图矩阵B(DB)中项目ik的位图覆盖记为Bit(ik),即位图矩阵的第k列.这个概念容易扩展到项集,项集X的位图覆盖记为Bit(X),如公式(14)所示. Bit(X)=∩i∈X(Bit(i)) (14) 在公式(14)中项集X的位图覆盖是一个编码向量,即项集X中的每一个项目的位图覆盖Bit(i)通过按位与运算得到.同样,对于两个项集X和Y,Bit(X∪Y)可由Bit(X)∩Bit(Y)计算得到. 表1和表2的示例中,设置效用阈值minutil=115.如表4所示,给出了由位图矩阵表示的整理之后的事务数据库. 表4 事务数据库的位图表示 3.2.2 项集修剪策略 改进的粒子群优化算法中将每个粒子编码成向量.编码向量由0或1组成的,表示粒子中某个项目不出现或者出现.如果在一个粒子中对应的第j位为1,就表示第j个位置对应的项目出现在项集中.否则,就表示第j个位置对应的项目没有出现在项集中.同时,每个粒子对应的编码向量的长度由事务数据库中高事务加权效用项集的数量决定.为了加速高效用项集的挖掘过程,需要修剪掉事务数据库中不存在的项集. 定义12.项集的编码向量的位图覆盖如果只由0元素构成,则该向量称为非期望编码向量(unpromising encoding vector,UPEV).反之,称为期望编码向量(promising encoding vector,PEV).项集的编码向量若为非期望编码向量,则该向量不可能是高效用项集.在高效用项集挖掘算法中去除非期望编码向量的项集,称为非期望编码向量修剪策略(unpromising encoding vector cut strategy,UPEVC).非期望编码向量修剪的伪代码由算法1给出. 算法1.非期望编码向量修剪策略 输入:表示粒子的编码向量Vec 输出:期望编码向量PEV BEGIN 1. 计算Vec中1的数量,记为VN 2. 用i1,i2,…,iVN表示Vec中包含的项目 3. RV = Bit(i1) 4. FORk从2到VNDO 5. | RV′ = RV∩Bit(ik) 6. | IF RV′是一个UPEV THEN 7. | | RV′ = RV 8. | | 将Vec中对应的ik从1变成0 9. | END IF 10.| RV = RV′ 11.END FOR 12.RETURN RV END 算法1的输入为一个粒子的Vec,输出为一个PEV.第1行计算出Vec中1的个数.第2行识别出Vec中1代表哪些项目.第3行用第1个项目的位图覆盖初始化最终结果.第4-11行进入循环,在循环中执行非期望编码向量的修剪.第12行返回最终结果.如果Vec是一个UPEV,通过算法1将会得到一个PEV,并且它是原始Vec的一部分.否则,原始Vec保持不变.在HUIM-IPSO算法(详见算法4)中,一旦生成新的粒子,就会使用算法1修剪该粒子,确保该粒子在事务数据库中真实存在. 3.2.3 轮盘赌选择法 轮盘赌选择法的基本思想是个体被选中的概率与其适应值的大小成正比,算法2给出了轮盘赌选择法的整体流程. 算法2以种群中所有的个体作为输入,输出被选中的个体.第1行算出每个个体的适应值.第2行根据公式(11)算出每个个体被选中的概率.第3行初始化一个空集RES.第4行算出每个个体的累积概率qk.第5-10行选出SN个个体保存在RES中.第11行返回选出个体的集合RES. 算法2.轮盘赌选择法 输入:种群中的每个粒子 输出:被选中的粒子RES BEGIN 1. 计算出种群中个体的适应值fitnessi 2. 根据公式(11)算出每个个体被选到下一轮的概率Si 3.RES=Φ 5. FORk从1到种群规模SNDO 6. | 在[0,1]区间内产生一个服从均匀分布的随机数r 7. | IFqk-1 8. | | 个体k→RES 9. | END 10.END 11.RETURNRES END 3.2.4 种群初始化 种群初始化的主要功能是随机生成若干个粒子,详细的初始化过程由算法3给出. 在种群初始化流程中,第1行扫描一遍事务数据库保留1-HTWUI.第2行将修剪后的事务数据库用位图矩阵表示.第4行随机生成一个数numi,并且1≤numi≤|1-HTWUI|.第5行设置Vec中有numi个1,其余都为0.项目ij被设为1的概率由公式(15)给出. (15) 式中,HN表示高事务加权1-项集的个数,即HN=|1-HTWUI|.由公式(15)计算出1-HTWUI的事务加权效用.该值越大的1-HTWUI在初始种群中被选中的概率就越大.第6-8行非期望编码向量修剪策略只会修剪numi>1的Vec.Vec中的每个位都表示一个1-HTWUI,所以这些1-项集一定被1个或多个事务所包含,这种类型的编码向量显然都是期望编码向量. 算法3.种群初始化 输入:事务数据库DB;种群包含的粒子个数SN; 输出:初始种群 BEGIN 1. 扫描事务数据库DB,去除1-LTWUI 2. 将调整后的事务数据库转为位图表示法的位图矩阵 3. FORi从1到SNDO 4. | 生成一个随机数numi 5. | 生成一个编码向量Veci并通过算法2将向量中numi个位设置为1 6. | IFnumi>1 THEN 7. | | 调用算法1生成新的编码向量Veci 8. | END IF 9. END FOR 10.RETURN 初始种群 END 3.3.1 算法设计 算法4第1行调用种群初始化算法3.第2行将初始迭代次数iter设为1.第3行将所有粒子经历过的最好的位置gbest设为空集.第4行将所有高效用项集的集合SHUI设为空集.第5-22行在循环中通过一个种群到下一个种群的迭代挖掘所有的高效用项集.第6-17行,种群中所有的粒子都需要进行效用值的检查.第7-9行,当迭代次数为1,种群中的粒子pi会被赋值给pbesti.第10行确定粒子pi对应的项集.函数IS通过项目i在粒子pi中对应的位置是否为1,返回相应的项集.第11-13行,产生的粒子表示的是高效用项集并且该高效用项集还没有被发现过,就记录下这个高效用项集.第14-16行更新当前粒子经历过的最好的位置.第18行记录下当前种群经历过的最好的位置.第19行通过算法2在当前种群的SHUI中选择下一代种群的初始优化值.第20行通过调用算法5来生成下一个种群.第21行更新迭代次数.最后,在第23行输出SHUI. 算法4.HUIM-IPSO算法 输入:事务数据库DB;效用阈值minutil;最大迭代次数max_iter 输出:高效用项集HUI BEGIN 1.调用算法3,得到初始种群 2.iter=1 3.gbest=Φ 4.SHUI=Φ 5.WHILEiter 6.| FORi从1到SNDO 7.| | IFiter==1 THEN 8.| | |pbesti=pi 9.| | END IF 10.| |X=IS(pi) //粒子pi对应的项集X 11.| | IFu(X)≥minutil∧X∉SHUITHEN 12.| | |X→SHUI 13.| | END IF 14.| | IFu(X)>u(pbesti) THEN 15.| | |pbesti=pi 16.| | END IF 17.| END FOR 18.| 将SN个粒子中效用值最大的添加到gbest 19.| 用算法2在SHUI中选择下一代种群的初始优化值 20.| 调用算法5 21.|iter++ 22.END WHILE 23.RETURNSHUI END 生成下一个种群时,HUIM-IPSO算法将公式(9)改为公式(16)来生成编码向量中需要改变的位置. vi=vi1+vi2+vi3 (16) 式中,vi1总是设为1;vi2和vi3分别由公式(17)和公式(18)给出. vi2=⎣|BitDiff(pi,pbesti)|·r1」 (17) vi3=⎣|BitDiff(pi,gbesti)|·r2」 (18) 公式(17)和公式(18)中,r1和r2是两个随机数;vi1表示随机接近最优值;vi2表示根据粒子pi和它之前经历过的最好位置的差异接近最优值;vi3表示根据粒子pi和所有粒子经历过的最好位置的差异接近最优值.其中两个编码向量之间的差异BitDiff,由公式(12)给出. 算法5描述了生成下一个种群的流程.第2-6行,首先通过反码运算随机改变粒子pi的编码向量中一个位置;然后通过反码运算随机改变粒子pi的编码向量中vi2个位置;最后通过反码运算随机改变粒子pi的编码向量中vi3个位置.第7行,调用子算法1确保生成的粒子真实存在. 算法5.生成下一代种群 输入:种群 输出:下一个种群 BEGIN 1.FOR 种群中的每一个粒子piDO 2.| 随机选择粒子pi的编码向量中一个位置,对其进行反码运算 3.| 通过公式(16)计算粒子pi的vi2 4.| 随机选择粒子pi的编码向量中vi2个位置,对其进行反码运算 5.| 通过公式(17)计算粒子pi的vi3 6.| 随机选择粒子pi的编码向量中vi3个位置,对其进行反码运算 7.| 调用算法1生成新的编码向量pi 8.END FOR 9.RETURN 下一个种群 END 3.3.2 算法演示 使用表1和表2的事务数据库来演示HUIM-IPSO算法.假设效用阈值minutil=115,表4给出了去除1-LTWUI并转化为位图矩阵的事务数据库.同时,假设种群的规模SN为3.由于1-HTWUI的个数为5,粒子经过编码得到编码向量有5个比特位.首先,将SHUI初始化为空集.为了生成第1个粒子,先随机生成一个数表示粒子的编码向量中1的个数.其次,使用公式(15)确定粒子的编码向量中哪些位置设为1.再次,假设第1个粒子对应的编码向量为“11110”,使用同样的方式可以得到另外两个粒子对应的编码向量.最后,假设第1个种群的三个粒子的编码向量如图1所示. 从图1中,得到第一个粒子对应的项集为{b,c,d,e}.根据算法3,RV被初始化为Bit(b).RV∩Bit(c)=0100011011∩1010100101=0000000001,由于结果是期望编码向量,RV更新为0000000001.下一步,RV∩Bit(d)=0000000000,结果为非期望编码向量,所以从p1中删除项目d,同时RV保留原来的值0000000001.接下来,RV∩Bit(e)=0000000001,由于结果是一个期望编码向量,最终RV=0000000001.最后,p1变成11010代表项集{b,c,e}被包含在事务T10中.因为u({b,c,e})=68 图1 初始粒子的编码向量 图2 第1个种群 Fig.1 Encoding vector of initial particles Fig.2 First population 类似的,p2也是期望编码向量,表示项集{b,d,e}.项集{b,d,e}出现在事务T2和T7,同时u({b,d,e})=166≥minutil,得到SHUI={{b,d,e}:166},其中冒号后面的数字表示项集的效用值.最后,p3代表项集{c,e}且不是一个高效用项集,SHUI保持不变.到目前为止,得到的第一个种群如图2所示. 由于是第1个种群,pbesti和粒子pi是一样的,即pbest1=11010,pbest2=10110,pbest3=01010.接下来,gbest是所有粒子中效用值最大的那个,这里gbest就是10110. 通过考虑粒子p1,演示如何生成下一个种群.随机选择粒子中的第5位,让它从0变成1,p1变成11011.假设随机数r1为0.5,BitDiff(p1,pbest1)={5},进一步v12=⎣1·0.5」=0,p1仍然保留11011.接下来,随机生成r2为0.8,BitDiff(p1,gbest)={2,3,5},进一步v13=⎣3·0.8」=2.因此,需要使用反码运算随机改变p1的两个位值.假设随机选择了p1的第2位和第3位,那么第2位从1变到0,第3位从0变到1,得到新的p1为101111,表示项集{b,d,e,f}.由于p1是一个期望编码向量,并且u({b,d,e,f})=66 使用同样的方法,也可以得到p2和p3的值.经过第2次迭代,假设SHUI={{b,d,e}:166,{b,e}:222},pbest1=11010,pbest2=10110,pbest3=10010,而gbest=10010. 在标准粒子群优化算法中,由于项集{b,e}是效用值最大的项集,它的编码向量10010会作为下一代种群的初始优化值.HUIM-IPSO算法中,项集{b,d,e}的编码向量10110也可能被选为下一代种群的初始优化值,并且它被选中的概率为166 /(166 + 222)≈0.428. 最后上面的过程一直重复直到达到最大迭代次数. HUIM-IPSO算法的时间复杂度,与传统的PSO算法时间复杂度一致.假设PSO算法中粒子的数量为m,迭代次数为N,每个粒子每一次迭代需要的运算时间为T.算法总的运行时间为m×N×T. 算法通过轮盘赌选择法在当前代种群的高效用项集中以一定概率选择下一代种群的初始优化值.该方法增加了种群的多样性,使得算法在每一次迭代中能够挖掘出更多的高效用项集.同时,算法通过非期望编码向量修剪策略删除了在数据库中不存在的项集,避免了算法去探索这些项集,进一步提高了算法挖掘出高效用项集的概率.因此在有限的时间内,算法能够挖掘出更多的高效用项集,算法挖掘高效用项集的收敛速度更快. 实验在Windows10操作系统,CPU AMD FX-8300八核 @3.3GH和内存 8GB下用JAVA语言实现. 实验中,共使用了4个公开的真实数据集retail[12],foodmart[13],mushroom[14]和chess[15].真实数据集的有关信息如表5所示.其中,事务数据库的密度表示事务平均包含的项目数量与数据库项目总数的比值.事务数据库的密度也代表数据的稀疏性. 表5 几个真实事务数据库的数据统计 retail是稀疏的数据集,它来自比利时的一个匿名零售商店.这个数据集中包含了88162个不同的事务和16470个不同的项目.foodmart是稀疏的数据集,包含零售商店4141个顾客的交易记录,具有1559个不同的项目.mushroom是一个来自奥杜邦协会北美蘑菇野外指南的数据集,包含8124个记录和119个不同的项目.chess是University of California Irvine(UCI)中的chess数据集经过改进得到的,共包含了3196个事务和46086个不同的项目. 本小节共进行了两组实验.第1组实验,测试了HUIM-IPSO算法、HUIM-BPSO算法和HUPE-GRAM算法在不同数据集上挖掘出的高效用项集数量.第2组实验,测试了HUIM-IPSO算法、HUIM-BPSO算法和HUPE-GRAM算法在不同数据集上挖掘高效用项集的收敛速度. 4.3.1 挖掘出的高效用项集数量 实验1中的相关参数由表6给出.在所有数据集上不断减小效用阈值,运行HUIM-IPSO算法、HUIM-BPSO算法和HUPE-GRAM算法.各算法挖掘出的高效用项集数量由表7-表10给出. 表6 实验1算法参数 表7 在chess数据集上挖掘出的高效用项集数量 表8 在mushroom数据集上挖掘出的高效用项集数量 表9 在foodmart数据集上挖掘出的高效用项集数量 表10 在retail数据集上挖掘出的高效用项集数量 观察表7-表10,发现在各个效用阈值下,HUIM-IPSO算法挖掘出高效用项集的数目都是最多的,HUIM-BPSO算法次之,最后是HUPE-GRAM算法.表9中发现在foodmart数据集上HUIM-BPSO算法和HUPE-GRAM算法都不能在有效时间内挖掘出任何高效用项集,HUIM-IPSO算法仍然能挖掘出大量高效用项集.表10中发现所有的算法都不能挖掘出任何高效用项集.因此HUIM-IPSO算法相较于HUPE-GRAM算法和HUIM-BPSO算法,能够在规定的时间内挖掘出更多的高效用项集. 4.3.2 挖掘高效项集的收敛性 实验2比较了不同算法的收敛速度.实验2设定使用相同的效用阈值来挖掘同一数据集中的高效用项集,迭代次数从200-2000次不断增大.实验参数由表11和表12给出.实验2结果如图3所示. 表11 实验2算法参数 表12 实验2不同数据集使用的效用阈值 图3 挖掘不同数据集的收敛性 通过观察图3,发现HUIM-IPSO算法能够通过较少的迭代次数,挖掘出更多的高效用项集.其他算法挖掘高效用项集的数量要么一直很小,要么随着迭代次数的增加挖掘高效用项集的数量会产生较大波动.该组实验结果说明,HUIM-IPSO算法能够在各种数据集上很好地挖掘出高效用项集并且具有很好的收敛性. 实验显示HUIM-IPSO算法能够通过较少的迭代次数挖掘出更多的高效用项集,算法有很好的收敛性.算法使用了轮盘赌选择法选择下一代种群的优化值.说明随机选择种群的初始优化值,能更加有效地遍历搜索空间.因此该方法提高了粒子群优化中种群的多样性,使得算法能够在更少的迭代次数中挖掘出更多的高效用项集. 本文针对基于粒子群优化的高效用项集挖掘算法在实际应用中存在的问题和不足,针对性地提出了一些新的思路和方法.本文的主要贡献如下. 提出了一种改进粒子群优化的高效用项集挖掘算法—HUIM-IPSO算法.算法使用了位图矩阵来表示事务数据库,使用了非期望编码向量修剪策略去除在事务数据库中不存在的项集,加快了项集的挖掘速度.算法还通过轮盘赌选择法在当前代种群的高效用项集中以一定概率选择下一代种群的优化值,增加了种群的多样性.这些策略最终使得算法相比HUPE-GRAM算法和HUIM-BPSO算法有更高的挖掘效率和更快的收敛速度.2.2 粒子群优化
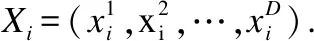
3 改进的粒子群优化高效用项集挖掘算法
3.1 算法总体思想
3.2 事务表示、项集修剪及种群初始化
3.3 HUIM-IPSO算法设计及演示

3.4 时间复杂度和收敛性分析
4 实验结果与分析
4.1 实验环境配置及编程语言
4.2 实验数据集
4.3 HUIM-IPSO算法挖掘高效用项集的对比实验

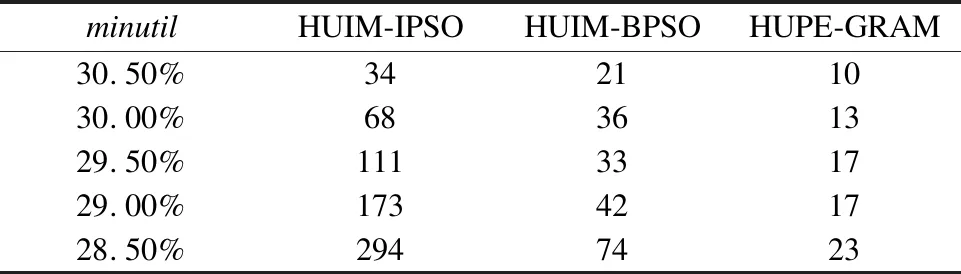
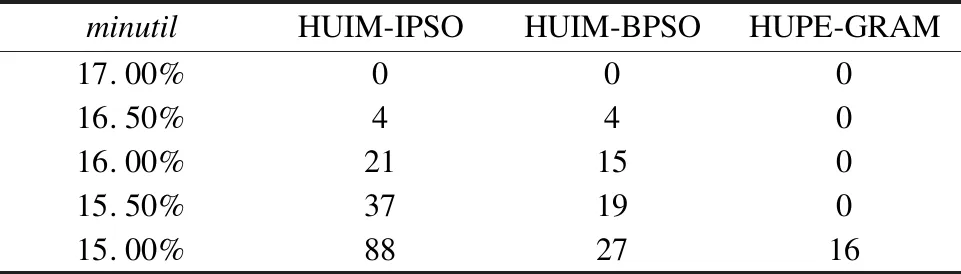
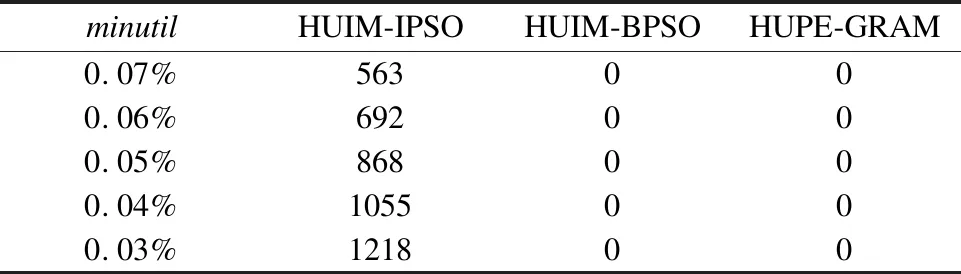
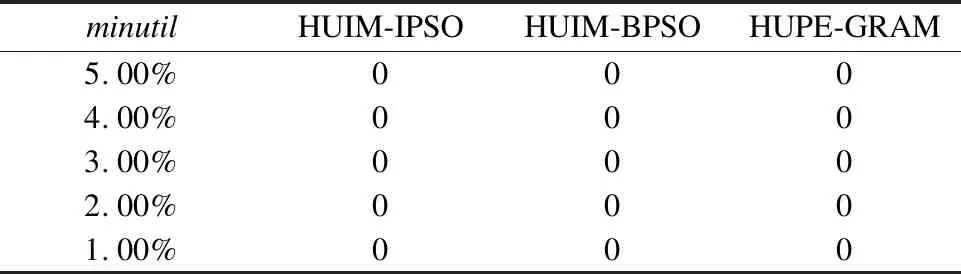


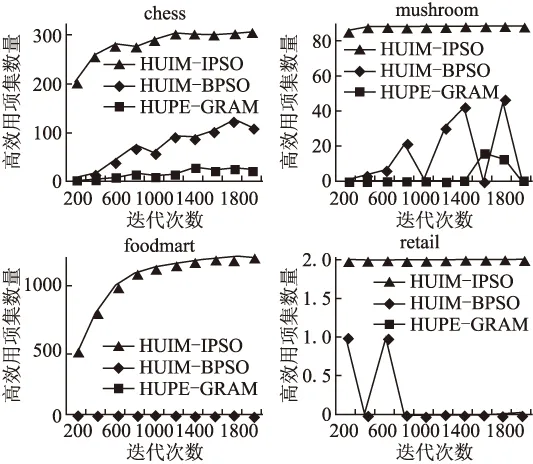
4.4 实验小结
5 结 论
