平面并联机构的形式化建模与验证

陈 琦，王国辉，张倩颖，施智平，陈善言，关 永

(高可靠嵌入式系统技术北京市工程研究中心，首都师范大学 信息工程学院，北京 100048)

E-mail：ghwang@cnu.edu.cn

1 引 言

并联机构是指含有两个或两个以上自由度且以并联方式驱动的一种闭环机构，它的动平台和静平台通过至少两个独立的支链相连接.常见的并联机构包括平面并联机构和空间并联机构.其中具有三自由度的平面并联机构在3D打印[1]、数控机床[2]等方面有着广泛的应用.它能够完成灵活、精细的抓取操作的同时具有较强的承载力，但这也增加了平面并联机构的控制难度.平面并联机构控制算法是为了解决工作空间[3]、奇异位置[4]、校对零位置[5]等问题而被学术界提出的，这些问题的研究基础是正运动学求解.正运动学求解[6]是指根据支链的杆长对动平台相对静平台的位置和姿态进行求解.常用的正运动学求解方法是D-H法，但它存在消元求解技巧性强、计算过程复杂等问题，极易导致求解过程错误.为了解决这一问题，学术界基于几何代数对平面并联机构进行了研究.例如：张立先[7]提出了基于几何代数的并联机构分析，利用旋量和关节速度的几何表示，研究并联机构的奇异性，但其表达式不够简洁.而相比于几何代数，共形几何代数[8](Conformal Geometric Algebra，CGA)具有几何概念清楚、物理意义明确、表达形式简单、代数运算方便等优点，便于工程应用中的几何解释、问题描述，极大地降低了机器人运动学的研究难度.因此，学术界基于CGA对平面并联机构进行了研究.例如：倪振松[9]提出了基于CGA的一种平面并联机构位置正解分析方法，建立了运动学正解模型.它是CGA在平面并联机构运动学应用的一个初步尝试.之后，针对3RPR平面并联机构，张英[10]提出了平面并联机构正运动学分析的几何建模和免消元计算，为平面并联机构运动学求解理论提供了一种新思路.以上算法都是基于特定机构进行研究，而黄昔光[6]提出的基于CGA的平面并联机构位置正解求解方法，是一种一般性求解方法，普遍适用于所有平面并联机构，但该方法仍处于数值验证阶段.因此，本文基于CGA对平面并联机构的正向运动学求解方法进行形式化建模与验证.

与基于计算机代数系统等传统方法不同，形式化方法是是建立在严格完备的数学基础上，采用精确数学语义的推理方法[11].它可以根据数学逻辑的严密性来提高发现微小错误的机率，具有较强的准确性和完备性.目前形式化验证技术主要有以下两种：模型检验和定理证明.模型检验[12]是将系统表达为有限状态机的自动验证技术.定理证明[13]是将研究内容建立物理模型，提取属性性质后转化成数学模型，根据语言规范和运算变成逻辑模型.与模型检验相比，定理证明不仅可以处理大规模的系统，而且可以对无限状态系统进行推理，拥有更好的灵活性.因此，本文采用定理证明的方法.常见的定理证明器有：ACL2、Mizar、Coq、PVS、HOL等，其中HOL家族中HOL Light[14]是最流行的定理证明器之一，它包含了高效的证明策略和丰富的数学定理库，如：几何代数库、共形几何代数库、实分析库、多维向量库等，而且使用了更加简单易懂的逻辑核心，能够准确检查定义和定理的形式化表达的正确性，使系统更加轻便、高效、简洁，为我们接下来的工作提供了重要的保障.本文选择HOL Light对CGA进行验证.

目前，几何代数形式化工作也取得了一些成果，例如：李黎明[11，15]完成了几何代数库的搭建，形式化证明了几何代数结构及基本运算，为我的工作奠定了理论基础.马莎[8，16]完成了共形几何代数库的搭建，形式化验证了几何表示和几何变换，同时，建立了5-R 串联机器人位置逆解和串联机器人抓取算法的模型，但目前并没有对并联机构进行形式化建模与验证.

本文以几何代数、CGA的高阶逻辑表达为基础，在HOL Light定理证明器中形式化描述了平面并联机构相关数学理论，通过运动变换等效模型、点运动变换表达式方程、杆长约束方程、位置正解封闭方程组实现平面并联机构正向运动学的高阶逻辑模型的建立，形式化分析与验证正向运动学的一般性求解算法，验证位置正解方程与一元六次方程的等价性，从而确保平面并联机构运动学分析的正确性和分析求解方法的可靠性.

2 基于CGA的刚体运动的形式化

几何代数是一种用于描述和计算几何问题的代数语言，实现了高维几何计算与几何分析的统一[16]，使其成为连接几何和代数的统一的描述性语言.几何代数包括三种重要的运算积：外积、内积和几何积.外积主要用于几何体的构建，内积主要用于距离与角度的计算，几何积主要用于运动的描述.表1是几何代数的运算符号.

表1 几何代数的运算符号

内积是一个降维运算，它与向量代数中的标准内积不同.几何代数的内积运算对象既可以是同维度空间对象也可以是不同维度空间对象，它能表示空间对象的距离、角度等几何表达.Inner是HOL Light中定义的高阶逻辑函数，表示几何代数的内积运算.

外积是一个升维运算.Outer是HOL Light中定义的高阶逻辑函数，表示几何代数的外积运算.当向量a，b线性相关时，其外积为零.此外，外积也满足反对称性.

几何积是连接内积和外积的混合运算.对于向量来说，几何积等于其内积和外积之和.

下文是基于CGA的刚体运动的形式化.空间刚体运动主要包括旋转和平移.

定义1.旋转算子的旋量可表示为

(1)

可形式化如下：

|-∀tmn.Rotation_CGAtmn=cos(t/& 2)%mbasis{}-

sin(t/& 2)/(norm(multivecmoutermultivecn)%

(multivecmoutermultivecn))

其中，t，m，n是变量.“&”是将自然数类型(：num)转换为实数类型(：real)的运算符.“%”表示向量的数乘.为了保持类型统一，实数与mbasis{}相乘可以把实数类型转化为向量类型.函数norm是HOL Light中定义的高阶逻辑函数，输入变量是N维向量，输出结果是N维向量的范数.函数multivec可将向量转换为对应的多重向量的形式.

定义2.平移算子的旋量可表示为

T=1-(t1e1+t2e2+t3e3)e∞/2

(2)

其中，t=t1e1+t2e+t3e3为平移向量.

可形式化如下：

|-∀t.Translation_CGAt=mbasis{}-& 1/& 2%(t＄1%

mbasis{1}+t＄2%mbasis{2}+t＄3%mbasis{3})*null_inf

当运算对象为实数“*”表示数乘.当运算对象为多重向量时表示几何积.其中mbasis{i}表示静坐标的基底ei.t＄1%mbasis{1}+t＄2%mbasis{2}+t＄3%mbasis{3}表示平移向量.

定理1.旋转算子的共轭

旋转算子R的共轭

(3)

可形式化如下：

|-∀tmn.reversion(Rotation_CGAtmn)=cos(t/& 2)%mbasis(t/& 2)/(norm(multivecmoutermultivecn)%(multivecmoutermultivecn))

其中，reversion(Rotation_CGAtmn)表示旋转的共轭.通过旋转定义、共轭、几何积和外积的基本运算性质，结合策略REWRITE_TAC简化目标，进而利用策略COND_CASES_TAC拆分目标，最后使用向量基本运算性质实现定理1的形式化证明.该定理在刚体运动方程的共轭(定理4)中将被使用到.

定理2.平移算子的共轭

平移算子T的共轭

(4)

可形式化如下：

|-reversion(Translation_CGAt)=mbasis{}+& 1/& 2%

(t＄1%mbasis{1}+t＄2%mbasis{2}+t＄3%mbasis{3})*null_inf

通过平移定义、共轭的基本运算性质，结合有限集合相关定理对不同情况进行分类讨论，并使用实数推导策略完成定理2的形式化证明.

定义3.刚体运动的运动算子

在CGA中，旋转(定义1)和平移(定义2)在旋量下的复合是简单的几何积，所以刚体运动的运动算子

M=RT

(5)

可形式化如下：

|-∀tmnl.motor_CGAtmnl=Rotation_CGAtmn*

Translation_CGAl

其中，t，m，n，l表示变量.其中，motor_CGAtmnl表示刚体运动算子.Rotation_CGAtmn表示旋转算子，它包含三个变量；Translation_CGAl表示平移算子，它包含一个变量.

定义4.刚体运动的运动算子

在CGA中，任意刚体o的刚体运动变化都可以借助几何积来实现，广泛适用于CGA中所有刚体的空间运动变换.它的表达式为：

(6)

其中，origid_motion为o变化后的刚体；M为规范化的运动变换算子.

可形式化如下：

|-∀xtmnl.geometry_CGAxtmnl=motor_CGAtmnl*

x*reversion(motor_CGAtmnl)

其中，x表示任意刚体，motor_CGAtmnl表示刚体运动的运动算子，reversion(motor_CGAtmnl)表示运动算子的共轭.

3 平面并联机构的形式化建模与验证

平面并联机构正运动学的一般性算法是指根据杆长的约束条件，建立1140种平面并联机构等效机构模型的普适方法.该算法可以解决实际生产过程中所有平面并联机构的正运动学问题.研究内容主要分为两部分：一是对平面并联机构等效模型的位置正解封闭方程组进行形式化建模；二是验证平面并联机构位置正解方程与一元六次方程的等价性.具体步骤如下：

S1：为了将具体的实际问题抽象成为CGA问题，需要建立运动变换等效模型，如图1所示.这一模型可以代表所有平面并联机构，通过这一模型就能够得到刚体运动算子方程.

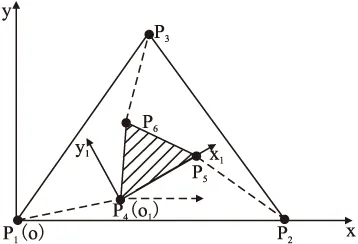
图1 平面并联机构等效模型

S2：基于这个等效模型，建立点运动变换后的表达式方程.接着，通过刚体运动算子方程，得到动平台的点在静平台下的坐标.

S3：将上述步骤求得的点坐标与杆长结合得到杆长约束方程.

S4：通过步骤2、步骤3的运算结果，建立了平面并联机构等效模型的位置正解封闭方程组.

S5：对封闭方程组的消简过程进行形式化验证.也就是验证平面并联机构位置正解方程与一元六次方程的等价性.

3.1 建立运动变换等效模型

图1为平面并联机构的等效模型，虚线表示连接动平台、静平台的等效运动支链，其长度为支链的实际长度.它是一个一般性的方法，普遍适用于所有平面并联机构.

取点P1为静坐标xoy的坐标原点，P1P2方向为x轴，三个静平台点坐标分别为P1(0，0)，P2(P2x，0)，P3(P3x，P3y)；取P4为动坐标x1o1y1的原点，P4P5方向为动坐标x1轴，点在动坐标x1o1y1中的坐标为P4(0，0)，P5(P5x，0)，P6(P6x，P6y).设点P4在静坐标xoy中的坐标为(Px，Py)，动坐标x1o1y1相对于静坐标xoy的姿态角为θ.平面并联机构正运动学的一般性算法就是已知三条等效支链的杆长q1(P1P4)、q2(P2P5)、q3(P3P6)，求点P4在静坐标的坐标(Px，Py)及姿态角θ.

动坐标到静坐标的运动变换可以看做三个点的变换过程，P4可看作静坐标中的P1沿x轴平移Px，沿y轴平移Py，再绕z轴旋转θ角得到，P5、P6也如此，这样子就可以得到P4、P5、P6在静坐标下的坐标.通过建立运动变换等效模型，得到刚体运动算子方程.

定义5.横向平移

静坐标沿x轴平移Px，即

(7)

可形式化如下：

|-∀Px.Translation_CGA_TxPx=mbasis{}-& 1/& 2%Px%mbasis{1}*null_inf

横向平移表示静坐标只沿着x轴移动Px.依据定义2平移算子的定义，横向平移中的mbasis{2}、mbasis{3}分别表示y方向与z方向.横向平移并未向这两个方向进行平移，所以它们前面的系数t＄2、t＄3均为零.

定义6.纵向平移

静坐标沿y轴平移Py，即

(8)

可形式化如下：

|-∀Py.Translation_CGA_TyPy=mbasis{}-& 1/& 2%

Py%mbasis{2}*null_inf

同理，定义6也如此.它表示静坐标沿着y轴平移Py，因此只包括mbasis{2}.

定义7.旋转公式

静坐标绕z轴旋转t，即

Rz=cos(t/2)-(e1∧e2)sin(t/2)

(9)

可形式化如下：

|-∀t.Rotation_CGA_Rzt=cos(t/& 2)%mbasis{}-

(mbasis{1}outermbasis{2})*sin(t/& 2)%mbasis{}

旋转公式表示静平台沿着z轴旋转t.依据旋转算子、外积的运算性质，可得norm(mbasis{1}outermbasis{2})等于1，可以省略norm(multivecmoutermultivecn)不写.因此，旋转算子简化为上式所示.

定义8.模型的刚体运动算子

该模型的刚体运动算子为

M=TxTyRz

(10)

可形式化如下：

|-∀PxPyt.M_CGAPxPyt=Translation_CGA_TxPx*

Translation_CGA_TyPy*Rotation_CGA_Rzt

刚体运动算子就是旋转和平移的几何积.本文建立的运动变换等效模型包括两次平移和一次旋转，即模型的刚体运动算子表示为它们三者的几何积.

定理3.刚体运动算子方程

刚体运动算子方程表示如下：

(11)

可形式化如下：

|-∀tPxPy.Translation_CGA_TxPx*

Translation_CGA_TyPy*Rotation_CGA_Rxt=

cos(t/& 2)%mbasis{}-

(mbasis{1}*mbasis{2})*sin(t/& 2)%mbasis{}-

(& 1/& 2*Px*cos(t/& 2)+& 1/& 2*Py*

sin(t/& 2))%(mbasis{1}*null_inf)-

(& 1/& 2*Py*cos(t/& 2)-& 1/& 2*

Px*sin(t/& 2))%(mbasis{2}*null_inf)

该式为刚体运动算子方程.通过横纵向平移、旋转公式的定义和几何积等于外积的性质，结合策略SIMP_TAC化简目标，继而通过几何积的自动证明策略CONV_TACGEOM_ARITH自动解算各种积运算的混合表达式实现刚体运动算子方程的证明.

定理4.刚体运动方程的共轭

刚体运动算子方程的共轭表示如下：

(12)

可形式化如下：

|-Reversion(Translation_CGA_TxPx*

Translation_CGA_TyPy*Rotation_CGA_Rxt)=

cos(t/& 2)%mbasis{}+(mbasis{1}*mbasis{2})*

sin(t/& 2)%mbasis{}+(& 1/& 2*Px*cos(t/& 2)+

& 1/& 2*Py*sin(t/& 2))%(mbasis{1}*null_inf)+

(& 1/& 2*Py*cos(t/& 2)

该式刚体运动算子方程的共轭.该定理的证明步骤与定理1、定理2的证明步骤类似.

3.2 建立点运动变换后的表达式方程

首先，先定义平面上的点坐标，即P1、P2、P3在静坐标下的坐标，P4、P5、P6在动坐标下的坐标；接着，定义点变换的表达式方程，这里会涉及刚体运动算子方程、刚体运动算子方程的共轭.通过点变换的表达式方程，可以得到P4、P5、P6在静坐标下的坐标.

定义9.平面点坐标方程

在CGA中，点可以写成

S=s+s2e∞/2+e0

(13)

其中，s=s1e1+s2e2+s3e3，s1、s2、s3为三维欧式空间点的坐标.

可形式化如下：

|-P.point_planeP=P$1%mbasis{1}+P$2%mbasis{2}+(& 1/& 2*(PdotP)%null_inf+null_zero)

该式为平面点的表达式方程.S＄1表示x轴上的系数，即s1；S＄2表示y轴上的系数，即s2.在平面中，点坐标是二维的，只包括x轴和y轴，所以平面中的点只包括mbasis{1}和mbasis{2}.其中，dot是HOLLight中定义的高阶逻辑函数，表示向量的点积.

pow是HOLLight中定义的高阶逻辑函数，输入变量是两个实数x、y，输出结果是xy，P1、P2、P3在静坐标中的表示如表2所示，P4、P5、P6在动坐标中的表示如表3所示.

表2 P1、P2、P3在静坐标中的表达式

定义10.动坐标的点P4、P5、P6在静坐标xoy的坐标

可形式化如下：

|-∀pM_CGA.point_transpM_CGA=M_CGA*p*

(reversionM_CGA)

该式是把动坐标的点转化为静坐标下.运用3.1中的刚体运动算子方程M_CGA可以得到动坐标的点P4、P5、P6在静坐标下所对应的坐标.

表3 P4、P5、P6在动坐标中的表达式

3.3 建立杆长约束方程

上面已经得到了每个点在静坐标下所对应的坐标.接下来需要根据各支链的杆长约束方程，建立点与点的约束方程，把点与点建立关系.

定义11.杆长约束方程

内积与距离的表达式方程：

P·S=-(s-p)2/2

(14)

可形式化如下：

|-get_square_qab=-& 2%(ainnerb)

根据2个点P、S的内积与距离的关系，建立杆长约束方程，该方程表示2个点P、S的内积与距离的关系.这里的get_square_qab指的是a与b两点实际距离的平方.

定义12.P1、P4约束方程

可形式化如下：

|-∀PxPy.-& 2%

(point_plane_P1innerpoint_plane_P4PxPy)=

get_square_qpoint_plane_P1(point_plane_P4PxPy)

定义13.P2、P5约束方程

可形式化如下：

|-∀tPxPyP2xP5x.-&2%(point_plane_P2P2x)inner

(point_trans(point_plane_P5P5x)(M_CGAPxPyt))=

get_square_q(point_plane_P2P2x)(point_trans

(point_plane_P5P5x)(M_CGAPxPyt))

定义14.P3、P6约束方程

可形式化如下：

|-∀tPxPyP3xP6xP3yP6y.-& 2%

(point_plane_P3P3xP3yinner(point_trans

(point_plane_P6(P6x：real)(P6y：real))

(M_CGA(Px：real)(Py：real)(t：real))))=

get_square_q(point_plane_P3P3xP3y)

(point_trans(point_plane_P6P6xP6y)

(M_CGAPxPyt))

3.4 建立位置正解封闭方程组

结合点运动变换后的表达式方程和杆长约束方程，建立位置正解封闭方程组.

(Px)2+(Py)2=(q1)2

(15)

(Px)2+(Py)2+(P2x)2+(P5x)2-2(P2xP5x-PxP5x)cosθ+2P5xPysinθ-2PxP2x=(q2)2

(16)

(Px)2+(Py)2+(P3x)2+(P3y)2+(P6x)2+(P6y)2+

2(PyP6y+PxP6x-P3xP6x-P3yP6y)cosθ+

2(PyP6x-P3yP6x-PxP6y+P3xP6y)sinθ-

2PyP3y-2PxP3x=(q3)2

(17)

定理5.P1、P4封闭方程

可形式化如下：

|-∀PxPy.Pxpow2%mbasis{}+Pypow2%mbasis{}=

get_square_qpoint_plane_P1(point_plane_P4PxPy)

定理6.P2、P5封闭方程

可形式化如下：

|-∀tPxPyP2xP5x.Pxpow2%mbasis{}+Pypow2%mbasis{}+P2xpow2%mbasis{}+P5xpow2%mbasis{}-

& 2%(P2x*P5x-Px*P5x)%cost%mbasis{}+

& 2%P5x%Py%sint%mbasis{}-

& 2%(Px*P2x)%mbasis{}=

get_square_q(point_plane_P2P2x)

(point_trans(point_plane_P5P5x)(M_CGAPxPyt))

定理7.P3、P6封闭方程

可形式化如下：

|-∀tPxPyP3P6P3xP6xP3yP6y.Pxpow2%mbasis{}+

Pypow2%mbasis{}+P3xpow2%mbasis{}+

P3ypow2%mbasis{}+P6xpow2%mbasis{}+

P6ypow2 %mbasis{}+& 2%(Py*P6y+

Px*P6x-P3x*P6x-P3y*P6y)%cost%mbasis{}+

& 2% (Py*P6x-P3y*P6x-Px*P6y+P3x*P6y)%

sint%mbasis{}-& 2%(Py*P3y)%mbasis{}-

& 2%(Px*P3x)%mbasis{}=

get_square_q(point_plane_P3P3xP3y)

(point_trans(point_plane_P6P6xP6y)(M_CGAPxPyt))

定理5-定理7是平面并联机构等效模型的位置正解封闭方程组，其中t，Px，Py为待求量，其余变量都为已知机构参数.利用约束方程替换封闭方程，继而使用策略将点的表达式方程重写，通过化简得到位置正解封闭方程组，实现封闭方程组到二元一次方程组的变换，进而推导出一元六次方程.

3.5 封闭方程组的消简过程的形式化验证

验证平面并联机构位置正解方程与一元六次方程的等价性证明.结合P1、P4封闭方程、P2、P5封闭方程、P3、P6封闭方程得到Px、Py的二元一次方程组.

APx+BPy+D=0EPx+CPy+G=0

(18)

其中，

A=2P5xcosθ-2P2x

B=2P5xsinθ

C=2P6ycosθ+2P6xsinθ-2P3y

D=(q1)2-(q2)2+(P2x)2+(P5x)2-2P2xP5xcosθ

E=2P6xcosθ-2P6ysinθ-2P3x

G=(q1)2-(q3)2+(P3x)2+(P3y)2+(P6x)2+(P6y)2-2(P3xP6x+P3yP6y) cosθ+2(P3xP6y-P3yP6x) sinθ

为了简化后面代码的形式化描述，A～G的形式化表示如下：

A=& 2*P5x*cost-& 2*P2x∧

B=& 2*P5x*sint∧

C=& 2*P6y*cost+& 2*P6x*sint-& 2*P3y∧

D=get_square_qpoint_plane_P1(point_plane_P4Px

Py)-get_square_q(point_plane_P2P2x)

(point_trans(point_plane_P5P5x)(M_CGAPxPyt))+

P2xpow2%mbasis{}+P5xpow2%mbasis{}-

(& 2*P2x*P5x*cost)%mbasis{}∧

E=& 2*P6x*cost-& 2*P6y*sint-& 2*P3x∧

G=get_square_qpoint_plane_P1

(point_plane_P4PxPy)-get_square_q

(point_plane_P3P3xP3y)

(point_trans(point_plane_P6P6xP6y)(M_CGAPxPyt))+(P3xpow2+P3ypow2+P6xpow2+P6ypow2-& 2*(P3x*P6x+P3y*P6y)*cost+& 2*

(P3x*P6y-P3y*P6x)*sint)%mbasis{}

定理8.关于Px、Py方程组

可形式化如下：

|-∀PxPyABD.

(A*Px)%mbasis{}+(B*Py)%mbasis{}+D=vec0

|-∀PxPyCEG.

(E*Px)%mbasis{}+(C*Py)%mbasis{}+G=vec0

其中，vec0表示的是零向量.上式是Px、Py的二元一次方程组.结合封闭方程的定义square_q1、square_q2、square_q3，得到Px、Py的二元一次方程组.

Px、Py关于t的表达式如下：

(19)

定理9.Px关于t的表达式

可形式化如下：

|-∀ABCDEG.

((A*C-B*E)*Px)%mbasis{}=B%G-C%D

该式为Px关于t的表达式方程.对二元一次方程组进行消元，消去Py，得到定理9.利用移项化简实现逻辑推理.

定理10.Py关于t的表达式

可形式化如下：

|-∀ABCDEG.

((A*C-B*E)*Py)%mbasis{}=E%D-A%G

同理，消去Px，得到Py关于t的表达式.该定理的证明步骤与定理9的证明步骤类似.当A*C-B*E等于零时，表示该机构为退化构型，而本文讨论的是非退化构型，也就是本文只讨论A*C-B*E不为零的情况.

定理11.一元三次方程

其数学描述如下：

r1(cosθ)3+r2sinθ(cosθ)2+r3(cosθ)2+r4(sinθcosθ)+r5cosθ+r6sinθ+r7=0

(20)

可形式化如下：

|-∀r1r2r3r4r5r6r7ABDECG.

～(A*C-B*E=& 0)⟹r1=E1∧r2=E2∧

r3=E3∧r4=E4∧r5=E5∧r6=E6∧r7=E7

⟹(r1*costpow3+r2*sint*costpow2)%mbasis{}+

costpow2%r3+(sint*cost)%r4+cost%r5+

sint%r6+r7=vec0

r1～r7是与机构参数相关的常数，它是通过Maple16编程软件实现的.系数特别复杂因此很难使用传统的方法进行验证.该式是关于θ的方程，包含sinθ和cosθ.结合策略把Px关于t的方程、Py关于t的方程重写到P1、P4封闭方程square_q1中.在运算过程中，等号右边出现了cos4θ和sinθcos3θ，而等式左边不包含这两项，因此需要验证cos4θ和sinθcos3θ前面的系数为0，进而消去这两项.

引理1.a与其倒数相乘等于1(a不等于0)

可形式化如下：

|-∀t.inv(& 1+tan(t*inv(& 2))*tan(t*inv(& 2)))

*(& 1+tan(t*inv(& 2))*tan(t*inv(& 2)))=& 1

其中，inv是HOL Light中定义的高阶逻辑函数，函数的输入变量是实数，输出结果是该实数的倒数，且定义0的倒数仍然为0.当a不等于0时，它与其倒数相乘等于1.这里a=&1+tan(t*inv(& 2))*tan(t*inv(& 2))，因为a不等于零，所以它与其倒数相乘才等于1.为了证明定理12，需要结合该引理辅助证明.

定理12.一元六次方程

其数学描述如下：

w6t6+w5t5+w4t4+w3t3+w2t2+w1t+w0=0

(21)

式中，w0=r1+r3+r5+r7w1=2(r2+r4+r6)

w2=-3r1-r3+r5+3r7w3=4(-r2+r6)

w4=3r1-r3-r5+3r7w5=2(r2-r4+r6)

w6=-r1+r3-r5+r7

可形式化如下：

|-∀tr1r2r3r4r5r6r7E1E2E3E4E5E6E7

w1w2w3w4w5w6w0.

r1=E1∧r2=E2∧r3=E3∧r4=E4∧

r5=E5∧r6=E6∧r7=E7

⟹

w1=& 2%(r2%mbasis{}+r4+r6)∧

w2=(-& 3*r1)%mbasis{}-r3+r5+& 3%r7∧

w3=& 4%(-r2%mbasis{}+r6)∧

w4=(& 3*r1)%mbasis{}-r3-r5+& 3%r7∧

w5=& 2 %(r2%mbasis{}-r4+r6)∧

w6=-r1%mbasis{}+r3-r5+r7∧

w0=r1%mbasis{}+r3+r5+r7∧

～(cos(t/& 2)=& 0)

⟹

tan(t/& 2)pow6%w6+tan(t/& 2)pow5%w5+

tan(t/& 2)pow4%w4+tan(t/& 2)pow3%w3+

tan(t/& 2)pow2%w2+tan(t/& 2)%w1+

w0=vec0

4 总 结

平面并联机构是机构运动学研究的一部分，它的分析、求解一直广受学者们的关注.在平面并联机器人的求解过程中，CGA方法具有几何概念清楚、物理意义清晰、表达形式简洁的优点，极大地降低了机器人运动学研究的难度.本文以几何代数、CGA为数学基础，在高阶逻辑定理证明器HOL Light中，对平面并联机构建立模型并进行形式化验证，从而确保了算法的安全性和可靠性.本文中的形式化工作，不仅能填补验证在并联机构中的空白，而且为我们以后的相关工作奠定了基础，也为以后算法的验证积累了丰富的经验.此外，并联机构不仅包括平面并联机构，还包括空间并联机构.因此下一步工作将围绕基于共形几何代数理论的空间并联机构的形式化建模与验证展开.