一种面向枢纽现象的离群数据检测算法

马文强，赵旭俊，张继福，饶元淇

(太原科技大学 计算机科学与技术学院，太原 030024)

E-mail:mwq_93@163.com

1 引 言

离群点挖掘是数据挖掘中的一个重要领域，也被称作离群点检测.随着人工智能技术飞速的发展，对离群点检测研究的兴趣正在大大增加[1].Hawkins[2]将离群点定义如下：离群数据是数据集中偏离大部分对象的数据，它们的表现与大多数常规对象有着明显的差异，以至于让人怀疑它们可能是由另外一种完全不同的机制所产生的.但是，离群数据并不全是错误数据，离群数据中可能蕴含着极为重要的信息，并已广泛应用在许多领域，例如天文光谱[3]，信用卡欺诈[4]，网络异常检测[5，6]，道路交通异常[7]等.近年来，研究者提出了许多离群检测算法，其中基于k近邻(kNN)和逆近邻(RNN)的离群检测是重要算法之一.随着数据维度的增加[8]，一些数据对象(枢纽点)会经常出现在其他数据对象的kNN列表中，其逆近邻集合中包含的数据对象个数很多，同时，一些数据对象(非枢纽点)几乎成为不常见的邻居，其逆近邻集合中包含的数据对象个数很少或者为零，这种现象称为枢纽现象.

枢纽现象(Hubness)是高维空间学习中的一个普遍问题，在许多文献中将其作为一个新的研究方向[9，10].枢纽现象是“维度灾难”中与k近邻查询相关的概念，它是指数据对象出现在其他数据对象的kNN列表中的次数Nk(i)(即RNN).其出现的原因是由于随着数据维度的增加，导致数据对象的次数Nk(i)出现的分布出现向右偏斜，同时方差也随之增加.枢纽现象造成的后果是一些数据对象(hubs，称为枢纽点)会经常出现在其他数据对象的kNN列表中，同时，一些数据对象(antihubs，称为非枢纽点)会经常不出现或很少出现在其他数据对象的kNN列表中.非枢纽与离群数据在高维和低维数据上均存在着联系.本文针对离群检测中的枢纽现象，结合k近邻和逆近邻互补性能，分析了离群检测中的影响空间，并一种面向枢纽现象的双向近邻离群检测算法，HPOD算法.首先，算法引入并重新定义了对象的影响空间，在影响空间中，不仅考虑对象的k近邻的影响作用同时还考虑逆近邻的影响作用；其次，在HPOD算法的基础上引入了启发式信息，提出了改进算法HPOD2算法，有效的降低了k的取值，从而减少了算法的计算量和运行时间；最后，采用真实数据集对本文提出的改进算法进行了检测并证明了本文提出的算法要优于传统的基于枢纽现象的离群数据挖掘算法.

2 相关工作

传统的离群点检测算法，大致可以分为基于统计的离群检测[11]，基于距离的离群检测[12]，基于密度的离群检测[13，14]，基于近邻的离群检测[15]，基于角度的离群检测[16，17]等.枢纽现象是高维数据中普遍存在的现象，而且随着数据集维数的不断增加，枢纽现象会越来越明显，被作为“维度灾难”的新方面和高维空间学习的一般问题进行了研究.

枢纽现象是“维度灾难”中与k近邻查询相关的概念，而k近邻查询是一个理论上比较成熟的方法，也是最简单的机器学习算法之一[18].加权k最近邻算法[19]是k近邻查询最简单、最有效改进算法，其主要思想是根据它们的距离来分配同一个权重的邻居，权重随着距离变化而变化，距离越近，权重越大，反之，距离越远，权重越小；LOF算法[20]通过k近邻查询计算对象的 k-距离、可达距离和可达密度，用数据对象k最近邻的平均可达密度与数据对象自身的可达密度之比表示数据对象的离群程度，但计算量大，不适合高维数据；还有LOCI算法[21]和LoOP算法[22]等很多算法都用到了k近邻查询.

逆k近邻查询是在k近邻查询问题的基础上产生的，获得将查询对象作为kNN的数据对象集合，逆k近邻可以评价查询对象的影响力，同样在离群数据挖掘方面也有广泛的应用.ODIN算法[23]是基于k最近邻图的入度(即逆近邻)来实现异常检测的算法，如果数据的入度小就可以被看做离群数据，但是需要人为设定区分度，不适用于未知数据集；INFLO算法[24]是一种基于密度的技术，在估计点的离群值时，除了直接邻居之外还考虑反向邻居的密度，是对LOF算法的扩展，解决了LOF算法对密度变化不敏感的缺点，但是只适合在低维和中维数据集，在高维数据集中效果较差.在数据聚类方面，逆k近邻查询也得到应用，RNN-DBSCAN算法[25]用Nk(i)作为对观测密度的估计，不仅可以处理较大的密度变化，而且将阈值由两个降低到一个，减少了人为因素的干扰，但是k值的选择对RNN-DBSCAN算法有较大的影响；Radovanovic等人[26]提出了适用高维数据的AntiHub和AntiHub2算法.Antihub算法根据每个数据对象i的Nk(i)值来确定离群点，AntiHub2算法则是在Antihub算法的基础上同时考虑每个数据对象i的值Nk(i)及其k最近邻Nk(i)值，但是AntiHub算法只有在较大的k值上才能提高正常数据与离群数据的区分度，运算量代价昂贵，虽然AntiHub2算法可以在相对较小的k值获得较高的区分度，但是k的取值还是相对较大.Guo等[27]人在AntiHub2算法的基础上引入距离加权提出了WAntiHub算法，虽然提高了算法的准确性，但是并未解决AntiHub2算法所出现的问题，并且随着k值的逐渐增大，距离加权的效果逐渐降低.

综上所述，现有的大部分基于逆k近邻(RkNN)的离群挖掘算法主要使用逆近邻来检测离群数据.但是，这些算法需要较大的k值才能获得较高的正常数据与离群数据的区分度，运算量较大，耗费时间较长，并且未考虑k近邻等信息.

3 影响空间下的离群数据挖掘枢纽算法

现有的基于逆k近邻(RkNN)的离群挖掘算法均利用数据对象的Nk(i)值来确定离群值，文献[11]中算法在较低的k值上对正常数据与离群数据的区分度不高，主要是因为数据对象的Nk(i)值本质是离散的，要想得到较高的准确率，往往需要选择较大的k值，但是计算量较大，并且从未考虑k近邻因素.针对上述问题，提出了一种面向枢纽现象的离群数据检测算法(An Outlier Detection Algorithm for Hubness Phenomenon，HPOD)，算法利用对象的影响空间进行离群数据检测，同时考虑数据对象的逆近邻和近邻等信息，有效的消除只由逆近邻带来的局限性，提高了算法的准确率.为了进一步提高算法的性能，本文对HPOD算法进行了改进，提出了HPOD2算法，HPOD2算法在HPOD算法的基础上引入了启发式信息，可以减小k的取值，从而减少算法的计算量.

3.1 影响空间

针对现有的大部分基于逆k近邻(RkNN)的离群挖掘算法单纯只使用逆近邻来检测离群数据且并未考虑k近邻等原因，本文提出使用对象的影响空间来检测异常数据，同时考虑数据对象的逆近邻和近邻等信息，相关定义如下：

定义 1.数据对象p的k-距离.对∀p∈数据集D，p的k-距离，记作kdist(p)，定义为对象p和对象q之间的距离dist(p,q)，且满足：

1)至少有k个对象qi∈D，使得

dist(p,qi)≤dist(p,q)；

2)至多有(k-1)个对象qi∈D，使得

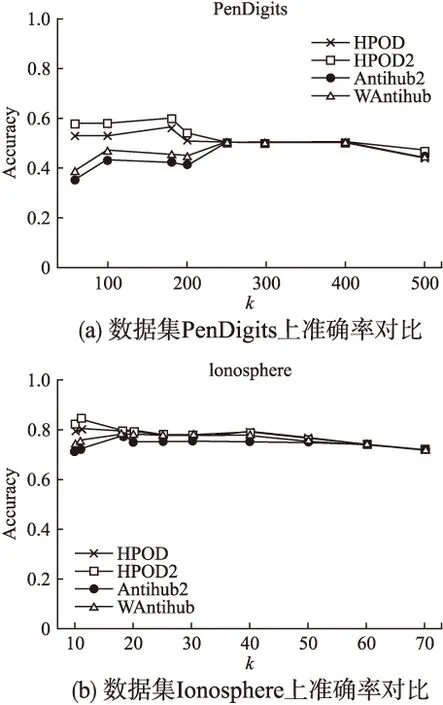
dist(p,qi)

定义 2.数据对象p的k最近邻集合.对p∈数据集D，p的k邻域点集NNk(p)，定义为数据集D的一个非空子集X，满足dist(p,X)≤kdist(p)即P的k邻域点集为

NNk(p)={X⊆D}dist(p,X)≤kdist(p)}

(1)

由定义1和定义 2可知，虽然数据对象p的k最近邻集合可能不是唯一的，但数据对象p的kdist(p)是唯一的.而且数据对象p的最近邻关系是不对称的.对于给定的数据对象p，p的最近邻可能并没有把数据对象p作为自己的最近邻之一.

定义 3.数据对象p的逆近邻集合.数据对象p的逆邻域点集RNNk(p)，定义为

RNNk(p)={q∈D|q∈NNk(p)}

(2)

由定义3可知对于任意数据对象p的k近邻数据集NNk(p)包含至少k个数据对象，而数据对象p的RNNk(p)取决于数据对象p作为其他点的k近邻次数可能为空，也有可能含有远远大于k个数据对象.而同时考虑数据对象p的RNNk(p)和NNk(p)，形成一个关于数据对象p的局部邻域空间，用来表示数据对象p的离群程度，定义如下：

定义 4.对象p的影响空间.数据对象p的影响空间ISk(p)，定义为对象p的k最近邻集合和逆近邻集合的交集，即

ISk(p)=NNk(p)∩RNNk(p)

(3)

由定义4可知离群数据都会较少或不出现在其他数据对象的近邻列表中，表示逆近邻集合包含的数据对象数量较少或者为空，其影响空间中包含的数据对象也会较少或不存在.采用对象的影响空间代替逆近邻进行离群数据检测，同时考虑数据对象的逆近邻和近邻等信息，可以消除只由逆近邻带来的局限性，有效减少误报率，除此之外，对象的影响空间同时考虑数据对象的逆近邻和近邻，对局部密度的变化有较高的敏感性，要优于其他方法.

3.2 HPOD算法

文献[25]利用数据对象的Nk(i)值来确定离群值，并选择全体数据对象中离群分数最小的n个数据对象作为离群对象，并未考虑数据对象的k近邻等因素.因此，根据定义4来定义对象的影响空间，并结合文献[25]，计算数据对象xi离群分数的标准化公式可重新定义为：

(4)

其中：ε为影响因子且ε∈[0,1]，dist(xi)为对象p的k-距离，sxi为数据对象xi的离群分数，Nk(i)为数据对象xi的逆近邻数量.

由公式(4)可得当数据对象xi为离群数据时，经常不出现或很少出现在其他数据对象的kNN列表中，其Nk(i)值较低，该数据对象的逆近邻所包含的数据对象也就较少，且数据对象的dist(xi)较大，sxi的得分也就越大.当数据对象的Nk(i)值较低时，其数据对象的dist(xi)则对数据对象的离群得分有较大的影响，从而保证了算法在较小的k值获得较高的正常数据与离群数据的区分度；虽然随着k值的增加数据对象的dist(xi)对数据对象的离群得分的影响逐渐降低，但数据对象的Nk(i)值逐渐变大，对数据对象的离群得分的影响逐渐增加，能保证算法在较高的k值也能获得较高的区分度.综上所述，数据对象的影响空间，可以保证算法无论在较高或者较低的k值上都能保持一个理想的正常数据与离群数据的区分度.

影响因子ε的给定可以调节dist(xi)和Nk(i)所占的比重，使算法适应不同的场景应用.当待检测数据比较适合逆近邻检测时，可以将影响因子ε变小；当待检测数据比较适合用距离检测时，可以将影响因子ε变大.在一些极端的情况下，例如，当待检测数据过度分散时，采用逆近邻检测，准确率极低，甚至干扰检测结果，此时可以将ε设为1，只靠dist(xi)来检测数据；反之，当待检测数据对距离信息不敏感时，此时可以将ε设为0，只根据待检测数据的逆近邻信息来检测数据.极端情况下，计算数据对象xi离群分数的公式(4)则变为：

(5)

3.3 HPOD2算法

为了能够在相对较小的k值上获得较高的正常数据与异常数据之间的区分度，减少计算量与运行时间，本文提出了HPOD算法的改进算法，HPOD2算法.

HPOD2算法在HPOD算法的基础上引入了启发式信息，不仅考虑数据对象xi本身的离群分数sxi，同时还考虑其k近邻对象的离群情况.数据对象xi的k近邻对象的离群得分之和annxi计算公式定义如下：

annxi=∑xj∈NN(xi)sxj

(6)

其中：annxi是数据对象xi的k近邻sxj得分之和，数据对象xj则是xi的k近邻，sxj为数据对象xj的离群得分.

对于每个数据对象xi，HPOD2算法按比列将(1-α)*sxi与数据对象xi的k近邻的离群分数之和α*annxi相加，其中α为最大区分度比列，能最大限度的区分离群数据与正常数据.数据对象xi的离群程度计算公式为：

ssxi=(1-α)*sxi+α*annxi

(7)

其中：ssxi为数据对象xi的离群总得分，sxi为数据对象xj的离群得分，annxi为数据对象xj的k近邻sxj得分之和，α是最大区分比例，α∈[0,1].

4 算法描述

HPOD算法的基本过程为：第一步，对数据集中的每个数据对象xi计算其k近邻，根据数据对象的k近邻得到每个数据对象xi出现在其他数据对象的kNN列表中的次数Nk(i)和dist(xi)；第二步，根据公式(4)，计算数据对象的离群分数，得到sxi；最后，根据上一步得到的每个数据对象的离群分数，从中选取离群分数最高的n个对象作为离群对象.其算法描述如下：

算法：HPOD

输入：

数据集D={x1,x2,…,xn},其中，xi∈D,i∈{1,2,…,n}

近邻数量k∈{1,2,…,n}

影响因子ε∈[0,1]

输出：离群分数最高的n个数据对象

步骤：

1)For each i∈(1, 2,…, n) in D

2) 计算数据对象xi的k近邻，得到数据对象xi的Nk(i)值

3) 和dist(xi)

4)end for；

5)For each i∈(1, 2,…, n) in D

6) 根据公式(4)，计算数据对象的离群分数，得到sxi

7)end for；

8)End HPOD

HPOD2算法在HPOD算法的基础上同时考虑其k近邻数据，在计算数据对象xi的sxi得分的同时，还考虑其k近邻数据对象的s得分，通过设置step参数进行遍历，找到最大区分度比例α，区分度比列α通过最大限度地区分离群程度最大异常对象的异常值得分自动确定，并且由两个参数控制：离群值与最大识别率之比ρ(其中，ρ∈(0,1])和搜索最大区分度比列α时的步长step(step∈(0,1])，并在最大区分度比例α的基础上将数据对象xi的sxi得分和其k近邻对象的离群得分之和annxi相加，得到最后的数据对象的离群分数，从中选取离群分数最高的n个对象作为离群对象.其算法描述如下：

算法：HPOD2

输入：

数据集D={x1,x2,…,xn},其中，xi∈D,i∈{1,2,…,n}

近邻数量k∈{1,2,…,n}

影响因子ε∈[0,1]

离群值与最大识别率之比ρ∈(0,1]

搜索最大区分度比列α时的步长step∈(0,1]

输出：离群分数最高的若干对象

局部函数：discScore(ssxi,ρ)：对于ss∈Rn和ρ∈(0，1]，输出ss中的[nρ]最小成员中唯一项的数目，并除以「nρ⎤.

步骤：

1)For each i∈(1, 2,…, n) in D

2) 计算数据对象xi的k近邻，得到数据对象xi的Nk(i)值和

dist(xi)

3)end for；

4)For each i∈(1, 2,…, n) in D

5) 根据公式(4)，计算数据对象的离群分数，得到sxi

6) 根据公式(6)，计算数据对象xi的k近邻的离群分数之和

annxi

7)end for；

8)disc :=0；

9)For each α∈(0,step,2·step,…, 1)

10) For each i∈(1, 2,…, n)

11) 根据公式(7)，计算数据对象xi的离群分数，得到ssxi

12) end for；

13) cdisc :=discScore(ssxi,ρ) //计算α对应的区分度

14) If cdisc>disc

15) t:=ssxi；disc:=cdisc；

16) end if；

17)end for；

18)For each i ∈ (1, 2,…, n) in D

19) 根据得到的最大区分度α值和公式(7)计算数据对象的离群

分数

20)end for；

21)End HPOD2

算法的复杂性分析：

HPOD算法中，计算每个数据对象的k近邻之后，可以同时得到数据对象xi的Nk(i)值和dist(xi)，因此HPOD算法的时间复杂度为O(n2)；HPOD2算法在HPOD算法的基础上引入了启发式信息，还考虑其k近邻数据，除此之外，还需要计算最大区分度，因此HPOD2算法的时间复杂度为O(n2s)，其中s为计算最大区分度α值的时间复杂度.

5 实验结果

为了验证提出的基于数据对象的影响空间算法的有效性，选取真实数据集进行性能测试，并与AntiHub2算法和WAntiHub算法的实验结果进行了比较.AntiHub2算法和WAntiHub算法是两种常见基于枢纽现象的离群数据检测算法，其中AntiHub2算法分析了枢纽现象，并且证明了非枢纽点和离群数据存在着联系；WAntiHub算法是对AntiHub2算法的改进，在AntiHub2算法的基础上利用k近邻中的距离信息作为权值，对逆k近邻中的离群分数进行了加权.本文所有的实验测试，均在以下环境进行：Inter(R)Core(TM)i5-4200CPU，8GB内存，Windows7操作系统，IntelliJ IDEA开发平台，采用java语言实现了所提出的算法以及涉及的相关算法.

实验全部采用真实数据集进行验证，且真实数据集全部来源于ELKI库(1)https：// elki-project.github.io/datasets/，分别为Ionosphere、SpamBase和PenDigits.数据集Ionosphere包含351条数据和32个属性，其中包括126个离群数据；数据集SpamBase包含2588条数据和57个属性，其中包括50个离群数据；数据集PenDigits包含9878条数据和16个属性，其中包括30个离群数据.测试数据集的详细信息如表1所示.

表1 测试数据集信息

Table 1 Details of test data

数据集数量n维度d离群点数量PenDigits98781630Ionosphere35132126SpamBase25885750

5.1 验证对象影响空间的有效性

为了验证算法采用对象的影响空间的性能要优于其逆近邻，本文将HPOD算法、HPOD2算法、Antihub2算法和WAntiHub算法在数据集SpamBase上进行测试，算法都使用相同的参数，搜索最大区分度比列α时的步长step=0.001，离群值与最大识别率之比ρ=0.1，HPOD算法和HPOD2算法中的影响因子ε=0.5，然后将两者的实验结果进行比较.

图1 数据集SpamBase上性能对比

由图1可知，Antihub2算法和WAntiHub算法的准确率随着k值的增加而逐渐变高，在k取值900以后才一直维持较高的区分度，主要原因是数据对象的逆近邻数量是离散的，需要较大的k值才能获得较高的区分度；而HPOD算法和HPOD2算法在k取值30到50之间就能获得较高的区分度，远远小于Antihub2算法和WAntiHub算法中的k取值，并且随着k值的增加，一直具有较高的准确率，主要原因是HPOD算法和HPOD2算法引入了数据对象的影响空间，同时考虑数据对象的逆近邻和近邻等信息，虽然在k值较小的时候，只靠数据对象的逆近邻数量无法获得较高的区分度，但是数据对象的近邻因素对数据对象的影响较大，使得HPOD算法和HPOD2算法能在较低的k值上有较高的准确率.

由图2可知，在数据集SpamBase上，WAntiHub算法和Antihub2算法和HPOD2算法都随着k值的增加耗费时间逐渐增加，并且在相同的k值上，效率差别不大，HPOD算法；但是由图1可知，HPOD算法和HPOD2算法在较低的k值上就可以得到较高的准确率，而WAntiHub算法和Antihub2算法却需要较大的k值；从图4(c)中的数据集SpamBase上，可以看出在各自最优k值上HPOD算法和HPOD2算法耗费的时间要远远低于WAntiHub算法和Antihub2算法，主要是由于WAntiHub算法和Antihub2算法的k值较大，计算量变大，从而导致算法耗费时间变长.

图2 数据集SpamBase上效率对比

在图1和图2中还可以看出，HPOD算法比HPOD2算法的准确率低，但算法效率明显高于其他算法，主要有两方面的原因：一是HOPD2算法中需要设置步长，step值越小，在搜索最大区分度比例时耗费时间O(s)将越长(可参见第5节HPOD算法的时间复杂度分析)，而在HPOD算法中不需要这一步骤，因此HPOD2算法的执行时间会高于HPOD算法，并受到步长step值的直接影响；二是由于HPOD2算法在HPOD算法的基础上进行了改进，引入了启发式信息，考虑数据对象的k近邻对象的离群情况，提高了算法的准确率，但增加了算法的执行时间.

如果应用场景对效率要求高的情况下，可以采用HPOD算法，在牺牲一定的精度下保持较高的效率；如果应用场景对准确率要求较高，可以采用HPOD2算法.

5.2 算法性能对比

在验证了影响空间的有效性之后，使用真实数据集Ionosphere和真实数据集PenDigits对算法的性能进行实验测试，并对所有算法在效率和准确率上进行比较来验证改进算法的有效性.在这里所有算法使用相同的参数，对比的是HPOD算法、HPOD2算法、Antihub2算法和WAntiHub算法在各自选取最优的k值时的准确率及其效率.

图3表明，在真实数据集Ionosphere和真实数据集PenDigits上，HPOD算法和HPOD2算法的准确率都要高于AntiHub2算法和WAntiHub算法，主要原因是HPOD算法和HPOD2算法引入对象的影响空间进行离群数据检测，同时考虑数据对象的逆近邻和近邻等信息，可以有效的消除逆近邻带来的在较低的k值上区分度不高的问题，提高了算法的准确率；在k取值较小时，WAntiHub算法的准确率要高于AntiHub2算法，主要是因为WAntiHub算法在AntiHub2算法的基础上引入了加权信息，从而提高了准确率，但是随着k值的增加，任意两个数据对象之间的k近邻中相同的数据对象会越来越多，两者距离慢慢地趋于一致，使基于距离信息加权的效果变差，并且WAntiHub算法同AntiHub2算法一样往往需要取较大的k值才能获得较高的准确率.

图3 真实数据集上算法准确率对比

由图4(a)和(b)可知，在相同k取值下AntiHub2算法和HPOD2算法的运行时间基本上相同，WAntiHub算法的运行时间略低于AntiHub2算法和HPOD2算法，但是相差不大，而HPOD算法的运行时间要小于其他算法；但是由图4(c)可以看出，所有算法为了获得最高的区分度而选取不同的k值情况，运行时间却是不同的.在数据集Ionosphere中，所有算法运行时间几乎没有差别，主要原因是数据集Ionosphere的数据量较小，在进行k近邻查询时耗时极少，差别不大；而在数据集PenDigits和SpamBase中HPOD算法和HPOD2算法所耗费时间要明显少于AntiHub2算法和WAntiHub算法，主要是原因数据集PenDigits和SpamBase数据量较大，而HPOD算法和HPOD2算法可以在较低的k值上获得最佳的正常数据与离群数据的区分度，而AntiHub2算法和WAntiHub算法则需要较高的k值，计算量的增加导致了算法运行时间变长，而且HPOD算法和HPOD2算法获得的最优区分度要高于其他算法的最优区分度.

6 结束语

针对在高维数据中进行离群数据挖掘导致出现的枢纽现象，提出了一种面向枢纽现象的双向近邻离群检测算法.该算法同时考虑影响空间中对象的k近邻和逆近邻对对象的影响作用；并且在HPOD算法的基础引入了启发式信息，提出了改进算法HPOD2算法，有效的降低了k的取值，从而大大提高了算法的效率；最后，对于本文提出的改进算法采用真实数据集对其进行了检测，实验表明本文提出的改进算法要优于传统的基于枢纽现象的离群数据挖掘算法.同时，面对海量高维数据，算法的并行化将是下一步的研究工作.

图4 真实数据集上算法效率对比