“导·学·讲·练·悟”教学模式下的物理规律教学研究

2020-05-13李俊永王长江陈亮

物理教学探讨 2020年4期

李俊永王长江陈亮

摘要：“導·学·讲·练·悟”教学模式是以学生学习为中心，以突出学生主体性地位为内涵，以发展能力为旨归，体现“学”为特点、“讲”为特色、“练”为特征、“悟”为特质的高效教学模式。文章着眼于导、学、讲、练、悟，以“机械能守恒定律”教学为例，探讨了该教学模式下的物理规律教学研究范式，进一步探索围绕教学五环节的教学范式研究之路，为物理教学理论提供实践支撑，以期丰富物理教学研究方式，开拓新的研究路径。

关键词：“导·学·讲·练·悟”教学模式;规律教学;机械能守恒定律

通过对“思维型”课堂教学理论的深入研究，我们认识到“思维型”课堂教学理论提出的四个教学环节虽然能够对具体教学实践起到指导作用，但是在操作层面往往会出现教学环节不完整，这既是理论问题又是实践问题。有鉴于此，从“思维型”课堂教学的基本原理出发并以此为重要理论根基，为使该理论具有更强的教学指导意义，我们提出了“导·学·讲·练·悟”教学模式，希望该模式能够成为沟通理论与实践的桥梁。以现行人教版物理必修2“机械能守恒定律”教学为例，对此加以阐释。

1 “导·学·讲·练·悟”课堂教学模式概述

“思维型”课堂教学理论认为，课堂教学中师生活动的核心是“思维活动”，通过引发学生积极思考、主动探究来加速认知过程。它强调以诱发思维动机为特征的教学导入，以引发思维动力为特征的教学过程，以进行思维监控为特征的教学反思，以达到灵活思考为目的的应用迁移。其核心部分为认知冲突、自主建构、应用迁移、思维监控四块[1]。

“导·学·讲·练·悟”课堂教学模式发源于该理论。其基本内涵是在教师的导引下调动学生的多感官，围绕学科基本知识主动、自发地进行自主学习，基于学习困惑积极、能动地进行小组合作学习，为发展学科能力、提升学科核心素养进行探究学习，最终实现导学目标。我们认为，在教学过程中，应显化并强调以诱发思维动机为特征的学本位式的“导”的环节，以引发思维动力为特征的自主建构式的“学”的环节，以触发思维广角为特征的“讲”的环节，以达到灵活思考为目的应用迁移式的“练”的环节，以进行思维监控为特征的学反思式的“悟”的环节，以体现“学”为特点、“讲”为特色、“练”为特征、“悟”为特质。

2 “机械能守恒定律”的教材分析

现行人教版物理必修2“机械能守恒定律”是继重力势能、动能、动能定理之后的一节内容，其后是关于能量守恒定律的介绍。本节课首先通过演示实验“小球能摆多高”引入，以“物体自由落体或沿光滑斜面滑下……由于惯性在空中竖直上升或沿光滑斜面上升”的说白构造情境，以“小孩松手后橡皮筋收缩，弹簧对模型飞机做功”插图为辅助，说明动能与势能的相互转化，并直接指出机械能的三种表现形式，以“物体沿光滑斜面滑下”“滑雪者沿斜面下滑时……只有重力做功”两幅插图为展现场景，结合动能定理、重力做功与重力势能变化的关系推导了机械能守恒定律，最后通过单摆运动阐释该定律的应用[2]。

如何做好这节课的教学，有3点值得思考：1.教材中该定律的描述有一个很重要的前提——忽略空气阻力、接触面光滑，从科学探究的角度讲，规律的学习应当从实际现象出发，那么教材“告诉式”（在理想化条件之下）的编排方式对学生思维能力提升究竟有多大帮助？2.科学方法未能体现，未能突出重力、弹力在机械能转化过程中的对等地位，未能让仅有弹力做功下的机械能守恒规律和仅有重力做功下的情形发生有机的联系。3.未把弹力做功下的机械能守恒与重力做功下的情形作比对，科学视域狭窄。

3 “导·学·讲·练·悟”教学模式下的物理规律教学

3.1 规律教学中“导”的研究

“导”的功能包括导向——揭示教学内容，导标——明细课堂任务，指导——学习方法提示，引导——避免盲目蛮干，定位——吸引学生注意。“导”立足于学生思维的发展，直接指向学习的核心，教师要为“导”注入源源不断的个性化的思想，力图体现以诱发思维动机为特征的学本位式的“导”的内涵。

通过教材解读本节有4项任务：1.知道何为机械能及动能与势能可以相互转化;2.理解机械能守恒定律成立的条件;3.经过情境分析与理论推导初步形成守恒思想，掌握规律的应用;4.通过能量守恒的教学树立科学观点，解决实际问题。教师需要让学生明白学习方法是什么。本节中，需要让学生从动能定理入手，紧扣机械能的概念，通过观察、分析，研究仅有重力做功下的机械能守恒与仅有弹力做功下的情形，建构较完备的知识结构。

开课前应当给学生展示导学目标及学习路径，以便学生做到心里有数。教学伊始，教师需要向学生呈现丰富的生活素材，如从高处飞落的瀑布产生巨大的能量，弹弓将石子抛出去，撑杆跳运动员越过横杆，秋千来回摆动等，以此充实认知表象。

“导”的策略：提出问题——引入新课。

问题1：观察、分析瀑布下落的过程中重力做功情况及动能和重力势能如何转化？

问题2：观察、分析弹弓抛石子的过程中弹力做功情况及动能和弹性势能如何转化？

问题3：分析撑杆跳运动员从助跑到越过横杆全程都有哪些能量相互转化？

借此总结出动能与势能（重力势能或弹性势能）可以相互转化以及机械能的概念。

设计说明：该教学片段补充、优化了教材内容，丰富了机械能转化类别，避免了教材中能量转化的单向研究。在多个情境中选取了3个镜头，观察、分析在有重力或者弹力做功时机械能相互转化的定性规律：（1）重力做正功，重力势能转化为动能;（2）弹力做正功，弹性势能转化为动能;（3）动能转化为弹性势能和重力势能，弹性势能转化为动能和重力势能。这样的设计，为科学、系统地学习机械能守恒定律做好了认知准备。

3.2 规律教学中“学”的研究

以引发思维动力为特征的自主建构式的“学”的环节是该部分的全部内涵，包括认知建构和社会建构。认知建构强调，学习是学习者积极主动建构的过程，知识是学习者经验的合理化;社会建构则强调师生互动、生生互动，应关注行为互动、情感互动。就课堂学习形态而言，表现为自学、互学、乐学等。因此，自主学习和互动学习是“学”的环节的关键构成。

在教材分析环节，我们已经提到教材始终让学生在理想化的条件之下分析问题，这不利于学生思维向纵深发展。那么，如何既能解决教材编写给教学带来的不足，又能高效地加速学生的认知发展。在此，我们因“导”诱“学”，立足现实物理情境，自主建构物理规律。

1.“学”的策略：因“导”诱“学”——规律建构。

如图1所示的演示实验——小球撞鼻子，细绳一端悬挂在铁架台上，另一端悬挂质量较大的小金属球。将细绳拉直并与竖直方向成较大角度且紧靠一名学生的鼻子（未画出）。由静止释放小球，当小球再次摆回来时，观察该学生的回缩反应动作。作为教师应引导学生分析该过程动能与重力势能转化的方向，并思考“回缩反应”是否有必要。

（1）因“导”诱“学”——定性分析1。

认知建构的关键问题：

问题1：在摆动过程中小球受到了哪些力？各力分别做何种类型的功？

问题2：“回缩反应”是否有必要？最关键的原因是什么？机械能怎么变化？

问题3：若将小球换成乒乓球，两者的机械能又将如何变化？哪个变化得更快一些？原因何在？

（2）因“导”诱“学”——定性分析2。

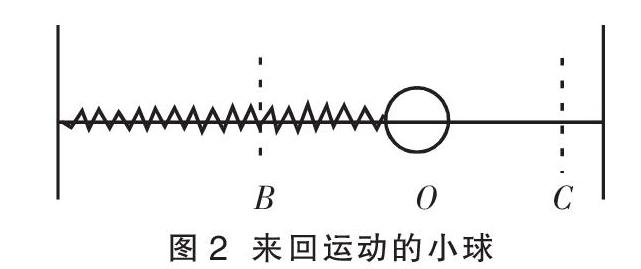
图2中水平放置的小金属球拴在一轻质弹簧上，中轴线上为一细丝，两端分别固定，O点位于平衡位置，先把小球拉离平衡位置到C点。

问题4：在运动过程中小球受到了哪些力？各力分别做何种类型的功？

问题5：能否回到C点？最关键的原因是什么？机械能怎么变化？

问题6：若将小球换成乒乓球，兩者的机械能又将如何变化？哪个变化得更快一些？原因何在？

设计说明：两组实验演示情境图为学生认真思考问题提供了依据，弥补了教材对弹力做功的苍白表述，逐步为实现机械能守恒定律内容的完备表述创造条件。两种情况下，运动过程中的阻力做功都将使机械能减少，但是在将金属小球换作乒乓球以后，对各自前后机械能变化快慢的分析，成为认知发展的重要节点。经分析便可知道，各阻力做功与重力做功或弹簧弹力做功相比较很少时，机械能减少得就比较慢，反之就快。当认为阻力可以忽略不计，则机械能守恒。此处设计有两个比较，同一演示实验先后不同操作下现象分析的比较，不同保守力做功参与下的平行比较。这样就顺利得到机械能守恒的条件，构造了与教材完全不同的教学路径。

2.“学”的策略：因“导”诱“学”——规律形成。

定性分析作为规律建构的先在思辨分析，需要理论推证增强分析结果的可信度。对两组演示情境分别取乒乓球的运动，以空气中摆动的乒乓球为例（如图3）。

问题7：能对乒乓球写出A—C过程动能定理的表达式吗？

问题8：A—C过程中重力势能的变化与重力做功关系的数学表达如何？

问题9：将你写出的两个式子综合起来，你能得到什么样的结果？请分析说明，并把该分析过程迁移到有弹簧弹力做功的情境中去。

问题10：请认真思考，除重力或者弹力以外的力不做功时，机械能将会怎样？

设计说明：通过反面揭示物理过程找到了建立机械能守恒定律的路径，体现了与教材截然不同的研究过程，同时也寻找到了机械能守恒的条件。这一连串的问题是学生自主学习的主要抓手，因此，为保证“学”的环节顺畅进行，精心设置关键问题是该教学模式在备课环节需要关注的焦点之一。

3.3 规律教学中“讲”的研究

“学”与“讲”是学生参与的重要外显行为，对掌握学习和提升教学质量至关重要。爱德加·戴尔发现并提出学习金字塔理论，揭示了不同的教学方式给学生带来的学习效果是不同的[3]。教学中应当发挥学生的主观能动性，让学生相互讨论，并讲出相关知识之间的来龙去脉;学生应当努力转变被动学习方法，要由被动听变为主动学，要多种器官综合使用[4]。“讲”的环节既涉及认知建构也涉及社会建构——生生互动、师生互动，该模式更看重社会建构。语言作为思维表达的有效工具，具有梳理思维、顺化思维、增强思维逻辑性与深刻性的功能。在认知建构的基础上，以合作学习的形式进行社会建构，把“问题”讲出来则学习效率将大大增强，以体现触发思维广角为特征的“讲”。

“讲”的策略：据“学”施“讲”——问题解决。

如图4所示，该环节学生将会围绕认知建构环节中的问题相互交流讨论，机械能守恒定律教学中，最应当理解和让学生讲出来的是该定律与动能定理之间的关系，该定律蕴藏了怎样的物理学思想或方法，又体现了什么样的物理观念。

行课至此，有必要活化、深化学生对该定律的认识。为此，需要解决的问题有以下几个：

问题1：加速度为g的物体机械能就守恒吗？反之就不守恒吗？

问题2：物体所受合外力为零，机械能就守恒吗？

问题3：系统所受到的合外力不为零，但合外力不做功或做功为零，系统机械能就守恒吗？

问题4：若系统无动能与势能的转化，能认为机械能守恒吗？

设计说明：在该阶段突出“讲”的功能，需要以“学”为铺垫，否则“讲”将会变成无本之木，无源之水。上述4个问题将会有力地帮助学生建构关于机械能守恒定律的正确认知图式，思维的张角因此变大。

3.4 规律教学中“练”的研究

在完成基本知识学习之后，掌握科学方法，形成和发展物理能力的教学任务亟需完成。能力形成最重要的特征就是能够在不同的情境中抓住问题本质，学会方法的迁移应用，并能够利用所学原理解释新现象、新问题。该部分力图体现为达到灵活思考为目的的应用迁移。

“练”的策略：析“变”抓“恒”——应用迁移。

从教材的例题出发（图3），把一个小球用细线悬挂起来，摆长为l，最大偏角为θ。如果阻力可以忽略，小球摆动到最低位置时的速度是多大？训练内容主要有：

问题1：分别选取悬点、最低点、释放点所在平面为零势能平面，列式计算会得到什么结论？

问题2：试利用机械能守恒定律的变式ΔEk=-ΔEP进行计算，有何心得？

在此基础上，可以进一步思考变式。

变式1，求解小球到达最低点轻绳的拉力;變式2，设细线的悬点距离地面高为h，当小球摆到最低位置时，摆线被拉断，求小球落地时的水平位移和速度大小;变式3，在悬点的正下方钉一个钉子D，小球从最大偏角为θ处摆下，则钉子到悬点的距离为多少时，小球恰好通过钉子的正上方。如此等等，不断变化条件改编教材习题，可以得到更多的变式。

设计说明：通过在变中求不变的不间断训练，有利于重新审视所学知识，增强知识的运用能力，一题多解，多解归一，一题多变，都是较好的研究策略。本环节中的3个变式，极大地拓展了学生的认知视野，为培育思维灵活性创造了新路子。

3.5 规律教学中“悟”的研究

“悟”的环节需要通过“启发式自问清单”撬动学生的思维，全程“反视”自己的学习历程。所谓“启发式自问清单”是指以自我发问的形式调动个人元认知的监控功能，所以教师对启发式问题的设置要巧妙构思，在实施过程中保持安静让学生思考整个过程，有可能的话让学生写出他们对本节课的认识，评价自己的学习过程。

借助图5所示的图谱，让思维的思悟活动更为清晰。

知识思悟清单：

问题1：什么是机械能？有哪几种类型，它们之间有何种联系？

问题2：机械能守恒定律的内容是什么？守恒条件是什么，与动能定理有何联系？

方法思悟清单：

问题3：你是经历了怎样的科学研究历程得到该定律的，都用到了哪些科学研究方法？

问题4：这些科学研究方法的有用性体现在哪里？请举例说明。

素养思悟清单：

问题5：你认为机械能守恒定律体现了什么样的科学观念？