地铁拥挤度和出行者异质性对时间价值的影响

刘建荣，黄 玲

(华南理工大学土木与交通学院，广州510640)

0 引言

公共交通中，车厢内拥挤会增加出行者的压力和不满意度，是影响出行体验的重要因素[1]，车厢内拥挤可能会影响出行者的时间价值.大部分学者利用陈述性偏好(Stated Preference,SP)方法获取数据，并利用Logit模型研究拥挤度的影响.分析文献，本文认为以下方面有待改进.

(1)出行者的异质性可能影响车厢内拥挤度的支付意愿.但仅有 Haywood[2]，Kroes[3]，Batarce[4]等少量文献考虑了出行者个体特征的影响.文献根据出行者的某些特征，如出行目的、性别等，将数据样本进行分类，进而分析不同子样本的出行选择行为.以上方法存在一定缺陷：当分类依据较多时，被划分出来的样本子集过多；数据样本的划分缺乏理论基础.

(2)除蒋盛川[5]，邵敏华[6]等的研究对象为中国公交系统，其他研究基本为发达国家或地区的研究成果.但各国对拥挤度的感知并不一致[7]，且由于生活水平、观念、公交系统服务质量的巨大差异，发达国家或地区的研究成果并不适用于中国.

考虑以上研究背景，本文选用潜在类别条件Logit模型(Latent-class Conditional Logit Model)研究出行者异质性和地铁拥挤度对时间价值的影响.潜在类别条件Logit模型能够根据出行者的选择行为对出行者进行类别划分，分析出行者个人特征对类别划分的影响，从而避免根据出行者某一特征进行盲目划分的缺陷.潜在类别条件Logit模型是在传统的Logit模型基础上发展起来的，较为复杂且出现较晚，故采用潜在类别条件Logit模型进行出行行为分析的文献较少.文献利用潜在类别条件Logit模型研究了出行选择行为，但均未涉及到拥挤度对出行行为的影响.

1 潜在类别条件Logit模型

1.1 模型基本原理

潜在类别条件Logit模型假定个人选择行为依赖于可观测的属性及潜在的异质性.潜在的异质性受研究者不能直接观测因素的影响.异质性通过离散参数变异来分析.

假定有N个顾客，每个顾客面临T个选择集，每个选择集有J个选项.如果在选择集t中，顾客n选择第j个选项，记ynjt为1，否则为0.每个选项由与选项相关的变量向量xnjt所表征，顾客n由一系列与顾客n相关的特征所表征.

潜在类别条件Logit模型假定N个顾客可以分为C个类别，每个类别的参数不一致，即β=(β1,β2,…,βC).如果顾客n属于类别c，则观察到他一系列选择的概率为

式中：xnjt为顾客n在选择集t中选项j的变量，其随个体n而变，也随选项j而变；βc为类别c的系数.

因为顾客属于哪个类别是未知的，因此需要指定顾客n的选择的非条件似然值，其值等于式(1)在所有类别上的加权均值.n属于类别c的概率可表示为

式中：θ是类别成员模型参数，θ=(θ1,θ2,…,θC-1) ，θC为识别参数时，θC设定为0；θc为类别c相关的类别成员模型参数；θl为类别l相关的类别成员模型参数，l为整数，取值范围1～C-1；zn为顾客n的个人属性，如性别，收入等.

样本的对数似然值是所有顾客的log非条件似然值之和，即

通过最大化式(3)求解参数值.

1.2 模型选择及模型拟合优度

样本总体类别数C在开始时是未知的，故需要预先指定C的取值.C取不同值，模型的对数非条件似然值之和取值也不一样.这就涉及到C的最优取值问题.采用ICAIC(Consistent Akaike Information Criterion)和IBIC(Bayesian Information Criterion)两个指标进行类别C的选择.ICAIC和IBIC的计算公式为

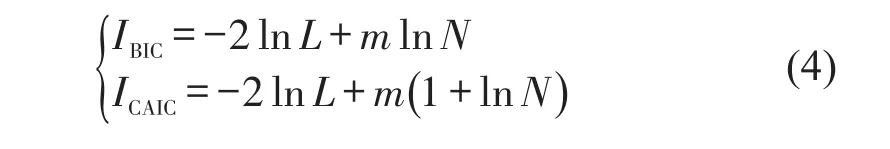
式中：L为最大样本对数似然值；m为模型的参数个数.ICAIC和IBIC值越小，模型拟合度越高.

关于潜在类别Logit模型的更多内容可见Bhat[8].

2 模型设定及问卷设计

2.1 模型设定

考虑不同类型地铁车厢座位数和空间的差异，选用站立乘客密度表征车厢内拥挤度.密度分为0.0，1.0，3.0，4.0，5.0，6.5人/m²这6个等级.

假定使用地铁的出行者分为C个类别.借鉴BATARCE[4]等，第c类出行者i对于选择集j的第k个选项的效用函数的可观测部分表示为

式中：c为虚拟变量，有座时为1，无座时为0；Pijk为对于出行者i，选择集j的第k个选项的地铁车票票价(元)；Tijk为对于出行者i，选择集j的第k个选项的乘坐地铁时间(min)；Dijk为对于出行者i，选择集j的第k个选项的地铁车厢内站立乘客密度(人/m2)，取值范围为[ 0.5,6.5 ；ηc、αc、βc、γc]为系数.

根据效用函数式(5)，出行者是在几种地铁系统中选择最合意的方式，地铁系统在车票价格、地铁乘坐时间和车厢内拥挤度等方面存在差异.

2.2 问卷设计

根据潜在类别条件Logit模型所需的数据格式，以及本文模型设定.问卷设计共包括3部分内容：出行者选择行为问卷，出行者个人统计学特征，出行者心理因素.

出行者选择行为问卷，使用SP调查方法，利用正交设计，共设置16个情景，每位被调查者对4个情景中的选项做出选择.

出行者个人统计学特征，对应式(2)中的zn设置具体的数据，如表1所示.

表1 个人统计学特征Table 1 Demographic characteristics

出行者心理因素部分，参考文献[9]等，结合我国地铁实际情况，设置对于交通方式的舒适性要求(lcomfort)这一潜在变量，选用4个显变量表征：Q1表示选择出行方式时，在意这种出行方式是不是拥挤；Q2表示选择出行方式时，在意环境舒适不舒适(如气味、温度、噪声等)；Q3表示如果某种出行方式不舒适，会选择更舒适的出行方式，即使要多付出5元以上；Q4表示如果某种出行方式不舒适，会选择更舒适的出行方式，即使要多付出15 min以上.显变量采用李克特五级量表进行调查，即1、2、3、4、5分别表示“完全不赞同”“有点不赞同”“不确定”“基本赞同”“完全赞同”.

3 实证分析

调查地点为南昌市地铁站，调查时间为2018年8月早高峰.共640人完整了问卷，每人回答4个假定情境，共回答2 560个假定情境.调查样本量符合要求，且出行者个体特征较符合使用地铁的群体.

3.1 潜在变量comfort的求解

选用Rasch模型求解潜在变量comfort，主要基于以下原因：潜在变量comfort的4个显变量的数据为定序数据.若将以上数据当作定距数据进行处理，实际就强加了定序数据之间间距相同的假定.Rasch模型主要用于定序数据分析，能够将被定序数据转化为定距和客观的数据.关于Rasch模型更详细地分析可见BOONE[10].

Rasch模型假定某人i对某一问题项j评价为q的概率表述为

式中：Pijq为某人i对某一问题项j评分为q的概率；τjq为step difficulty；θi、bj分别为与个人i和问题项j相关的一维定距数据，且为同一量纲(Logit).

利用极大似然估计对定序数据进行分析，得到Q1～Q4这4个问题项的IN MNSQ、OUT MNSQ、PTMEAS值信息如表2所示.IN MNSQ及Out MNSQ位于0.5～1.5，说明拟合度较好；PTMEAS介于0～1，显著大于0，说明显著性较好.故本文数据的拟合度较好.

表 2 Rasch模型统计参数信息Table 2 Estimation of item's difficulty and fit statistics

通过Rasch模型，还得到了与每位调查者相关的θ值.由于Q1～Q4这4个问题项均为出行者对于舒适性的要求，因此将θ值定义为出行者对于舒适性的要求(lcomfort)，lcomfort为一维定距数据，量纲Logit.由于每一位被调查者均有一个lcomfort，本文共调查640位出行者，有640个数据，数据量太大，在此不列出.

3.2 潜在类别条件Logit模型

使用stata中的lclogit工具包进行数据分析，关于lclogit工具包的更多细节，可以见说明书[11].对于潜在类别条件Logit模型，需要确定样本总体类别数量C.分别假定样本可被划分为2～5个子集，得到各子样本数量情况下的ICAIC和IBIC值如表3所示.当类别为2时，ICAIC和IBIC的值最小，样本可以分为2个子集.

表 3 模型ICAIC及IBIC比较Table 3 Comparison of values ofICAICandIBIC

将样本总体的子集数量设定为2，对样本总体进行潜在类别条件Logit模型回归，并将两个子类别分别定义为class1、class2.为对比潜在类别条件Logit模型是否能够提高对数据的拟合度，同时对数据进行传统的条件Logit回归.最终，潜在类别条件Logit模型的log likelihood值为-1 415，PseudoR2为0.202；传统的条件Logit模型的log likelihood值为-1 478，PseudoR2为0.166 8.因此潜在类别条件Logit模型对数据的拟合度优于传统的条件Logit模型.

潜在类别条件Logit模型的回归系数如表4中的class1、class2.为与传统方法进行对比分析，假定出行者不存在异质性，对数据整体进行传统的条件Logit模型回归，得到系数如表4中的“整体”部分.表4中class1、class2、“整体”中的回归系数，对应式(5).样本点的个体特征对分类的影响如表5所示.表5中是以class2为基准的，即将class2的各个系数设置为0，故在表中未列出.另外，表4中的“class1”“class2”，表5中的全部数据是同时估计的，但为了明显起见，分别列出.class1和class2占总体的比例分别为41.8%和58.2%.

表 4 潜在类别条件Logit模型回归系数Table 4 Regression coefficient of latent class conditional Logit model

表 5 出行者特征对类别的影响Table 5 Impact of demographic characteristics on classification

根据表4数据，class1类别中，γ不显著，即对于无座乘客，地铁车厢内站立乘客密度的增加不会对站立乘客的效用函数产生影响.class2中，γ显著小于0，即对于无座乘客，地铁车厢内站立乘客密度的增加会导致站立乘客的效用减少.因此class1中的无座乘客不在意车厢内拥挤度，而class2中的无座乘客极为在意车厢内拥挤度.

根据式(5)，有座、无座乘客的效用函数分别为

Vtime、分别表示乘客有座、无座时的时间价值(元/h)，即

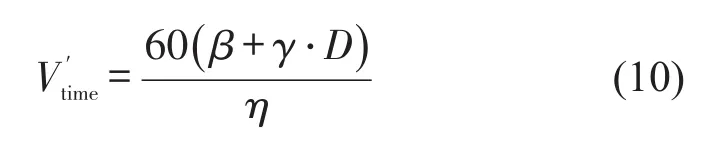
根据式(9)、式(10)及表4中数据，对于class1中的出行者，有座乘客与无座乘客的时间价值分别为14.7元/h、16.9元/h.无座乘客的时间价值是有座乘客1.16倍.对于class2中的出行者，有座乘客与无座乘客的时间价值为23.1元/h、(20+8.6⋅D)元/h.class2中出行者的时间价值大于class1中出行者的时间价值.对于class2的站立乘客，车厢内站立乘客的密度增加1人/m2，则时间价值增加8.6元/h，增加值极大.

对于class2的出行者及全部出行者，以有座乘客的时间价值为基准，将不同拥挤度情况下的无座乘客时间价值除以有座乘客的时间价值，得到不同拥挤度情况下的相对时间价值，具体如图1所示.随着车厢内无座乘客密度的增加，相对时间价值逐渐增加.

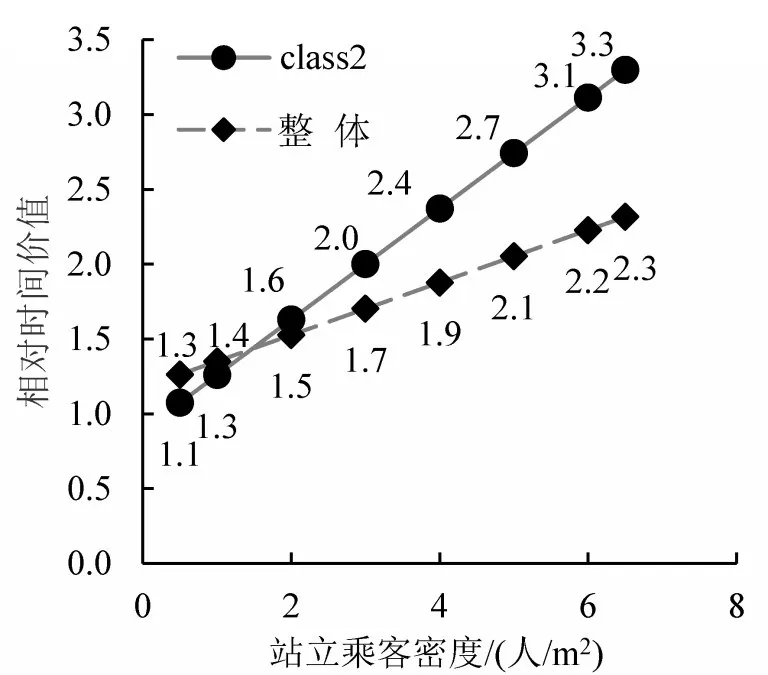
图1 不同密度情况下的相对时间价值Fig.1 Time multipliers under different standee densities

对于class2的出行者，当车厢内无座乘客密度为0.5人/m2时(只有很少的站立乘客，乘客在车厢内行动极为自由)，相对时间价值为1.1，即站立乘客的时间价值为有座乘客的1.1倍；当车厢内无座乘客密度为4人/m2时(有点拥挤，行动受到一定的限制)，相对时间价值为2.4，站立乘客的时间价值为有座乘客的2.4倍；当车厢内无座乘客密度为6.5人/m2时(极为拥挤，几乎不能移动)，相对时间价值为3.3，站立乘客的时间价值为有座乘客的3.3倍.分析图1中的class2和整体可以发现，当拥挤度超过2人/m2，同一拥挤度情况下，class2的相对时间价值大于整体的相对时间价值.因此若不考虑出行者的异质性，会低估地铁车厢内拥挤度对重视拥挤度的出行者(class2)的影响，且会高估地铁车厢内拥挤度对不在意拥挤度的出行者(class1)的影响.

分析表5数据，仅lcomfort的系数显著，且为负值.即lcomfort越大，出行者属于class2的概率越大.根据表5和式(2)，可以确定lcomfort的比例为exp(-0.157)=0.855.因此，lcomfort的1Logit，出行者属于class2的比例会减少14.5%，即1-0.855=0.145，因此lcomfort对出行者所有类别的概率具有很大影响.

4 结论

本文研究了出行者异质性和地铁车厢内拥挤度对地铁出行时间价值的影响.通过研究，得到以下结论：相比传统的条件Logit模型，潜在类别条件Logit模型对数据具有更高的拟合度；根据潜在类别条件Logit模型，出行者可以划分为class1和class2两个群体，占比分别为41.8%、58.2%，class1中无座乘客不在意车厢内拥挤度，class2中无座乘客极为在意车厢内拥挤度；class1中的出行者，有座乘客与无座乘客的时间价值分别为14.7元/h、16.9元/h，class2中无座乘客的时间价值分别为(20+8.6⋅D)元/h；出行者的舒适性需求对出行者类别划分具有显著影响，需求越高，出行者越有可能属于class2.