基于局部概率解的免疫遗传影响力最大化算法*
2020-05-13钱付兰张燕平
钱付兰,徐 涛,赵 姝,张燕平
1.安徽大学 计算机科学与技术学院,合肥 230601
2.安徽大学 信息保障技术研究中心,合肥 230601
1 引言
在线社交网络的流行引起人们对信息传播的极大关注。例如Facebook、Twitter、Microblog 和其他一些社交媒体。通过网络中朋友之间的“口碑传播”,一条信息很快就会传播整个网络。这种扩散现象已被证明很有应用前景,例如网络竞选。2016 年美国总统竞选活动,其中Twitter 几乎每天都被用作拉票竞选工具。社会网络的蓬勃发展,对其研究分析也显得越来越重要。社会网络研究有许多不同的研究方向,包括影响力最大化[1]、社团发现[2]和链路预测[3]等方向。
影响力最大化问题因其潜在商业价值而近来被广泛研究。该问题的形式化描述是在社会网络中寻找K个初始种子节点,使其通过社会网络关系的影响传播最终所产生的影响力延展度最大。Domingos 和Richardson 将该营销问题抽象定义成算法问题去求解[4]。Kempe 等人[5]首次将影响力最大化问题形式化为离散组合优化问题。他们证明该问题在独立级联(independent cascade model,IC)和线性阈值(linear threshold model,LT)传播模型下是一个NP 难优化问题,并提出爬山贪心算法。因为该算法需要数万次蒙特卡洛(Monte Carlo,MC)模拟[6],计算量非常巨大,不适用于大型复杂网络。
因此,本文提出IC 传播模型下有效的节点集影响力评估策略并且利用免疫遗传算法[7]处理复杂组合优化问题的优秀效果,提出基于免疫遗传的影响力最大化算法(immune genetic algorithm based influence maximization,IGIM),本文主要贡献如下:
(1)提出一种新颖有效的基于免疫遗传影响力最大化算法,该算法可以快速在大型复杂网络寻找到有影响力的种子节点。
(2)考虑到算法的运行效率,提出局部概率解节点集影响力评价函数作为IGIM 算法的适应值函数。
(3)为进一步加速算法的收敛,本文设计基于局部概率解适应值函数的启发式策略,加速算法的进化过程。
2 相关工作
近年来,很多研究者提出对影响力最大化问题算法效率的改进,可以分为两大类:(1)改进的Monte Carlo贪心算法。Leskovec 等人[8]提出CELF(cost-effective lazy forward)算法,该算法主要思想是利用子模性质来减少MC 模拟次数,降低时间复杂度。CELF 算法比传统贪心算法快大约700 倍。Wang 等人[9]提出贪婪算法与社会网络社团属性相结合的CGA(community based greedy algorithm)算法。CGA 算法思想是将网络划分成多个社团,从社团中利用贪婪策略选择种子节点降低模拟的复杂性。然而这些算法在大型复杂网络,时间复杂度依然很高。(2)基于启发式策略的影响力最大化算法。Chen 等人[10]基于度中心性提出DegreeDiscountIC 算法,该算法主要思想是当一个节点被选为种子节点后,考虑到影响重叠,计算此节点的邻居影响力时就要进行度折扣计算。Liu等人基于PageRank 算法拓展提出Group-PageRank算法[11],与仅能用于计算单个节点影响的传统Page-Rank 算法不同,Group-PageRank 可以在几乎恒定的时间内估计任何节点集之间的影响强度。Jung等人[12]提出IRIE(influence ranking influence estimation)算法,该算法使用少量的迭代来生成节点的全局影响力排名并结合简单的影响估计不断迭代调整种子节点集。这些算法忽略了扩散模型的性质,因此影响范围与扩散模型下的实际影响有明显差距。在IC 模型下,Kimura等人[13]第一个提出最短路径估计影响扩散SPM(shortest-path model)模型。SPM 通过Dijkstra算法获得从节点集S到任何节点v的最短路径,从而得到种子集的扩展,可以精确而有效地计算。同样的,Chen 等人[14]提出MIA(maximum influence arborescence)模型,该模型思路是影响力只沿节点间最大影响路径传播,并将节点影响范围局限在以节点为根的树状结构中。最近,有些工作是基于网络社区特征解决影响力最大化问题。Shang 等人提出CoFIM(community-based framework for influence maximization)算法[15],该算法分为两个阶段:种子扩展和社区内传播。基于传播过程,简化影响扩散估计,采用贪婪算法来选择种子节点。此外,许多工作利用智能优化算法解决影响力最大化问题。Jiang 等人[16]提出期望传播值(expected diffusion value,EDV)来近似计算节点组合的影响范围,并且提出基于模拟退火的影响力最大化算法SAEDV(simulated annealing expected diffusion value),从而可以更有效地解决影响力最大化问题。Gong 等人[17]提出离散粒子群影响力最大化算法DPSO(discrete particle swarm optimization)。该算法使用粒子群算法并结合度最大启发式策略和局部搜索方式加速算法收敛。Cui等人[18]使用度下降策略进行节点选择产生新节点集,并基于差分进化算法提出度下降的差分进化影响力最大化算法DDSE(degree-descending search evolution)。Şİmşek 等人[19]提出联合启发式策略重塑网络节点,以便群体智能优化算法在其目标函数状态空间上获得一般斜率,实验利用群体智能优化算法获得了很好的效果。除了以上的一些影响力最大化算法,Zhang 等人[20]提出采用精确概率解加策略计算影响力,并利用容斥定理证明精确概率解的计算,给出增量搜索策略来解决影响力最大化问题,极大地提高了算法的运行效率。以上方法在时间效率上和传播精度上并不能得到一个很好的平衡,也有些策略不适用于大型网络。
通过以上影响力最大化算法的研究与分析,现有算法并不能解决时间复杂度和传播影响范围之间的平衡问题。受到Zhang 等人和Jiang 等人工作启发,本文提出新颖的局部概率解影响力近似估计并采用免疫遗传优化算法寻找种子节点。
3 影响力最大化问题
本章将会给出影响力最大化问题形式化定义,并且介绍相关传播模型和影响力近似计算。
3.1 基本定义
在影响力最大化研究中,社交网络G=(V,E),其中V代表社交网络中的用户,E是对用户社交关系集合的建模。影响力最大化问题是在社会网络中找到一组大小为K的影响力最大的种子节点集S。σ(S)表示给定种子节点集S最终激活的期望节点数,即S的影响力。在特定传播模型M下,任意种子节点集S*的影响力可以表示为σG,M(S*)。通过以上对影响力的定义,影响力最大化问题形式化为:

3.2 传播模型
本文使用的传播模型为研究最为广泛的独立级联模型。IC 模型是以离散过程扩散,在此模型下用户只有两种状态:激活和未激活。在时间步骤t=0,给定初始种子集S0,每一个激活用户u∈St,将会以传播概率p尝试激活直接邻居v(未激活)并且只有一次机会,如果激活失败节点u将不会再影响节点v。在t+1 时刻,v∈St+1的概率为(1-p)l,l为节点v所有激活邻居的数量。该过程持续到没有新的用户被激活为止。
3.3 影响力近似估计
Zhang 等人从传播概率角度出发提出精确概率解加影响力估计策略,并证明该策略影响力计算遵循容斥定理(inclusion-exclusion,IE)。如图1 所示,假设节点1 为种子节点,节点5 被影响的路径有两条,分别是P1→2→5和P1→3→5。根据容斥定理计算节点5 激活概率为:

因此得出节点1 的影响力评估为:


Fig.1 Small network图1 小型网络
在复杂大型网络中,给定单个节点v所有入度邻居{ui|ui→v} 和传播概率pu,v,计算节点v的激活概率,可根据式(4)计算。Zhang 等人工作虽然极大地提高节点集影响力评估效率,但是该方法在全网络进行计算,仍然耗费许多时间。为了高效评估节点集的影响力,本文提出局部容斥概率解适应值函数,将会在4.2 节介绍。

其中,k表示节点v入度节点数量。
4 免疫遗传影响力最大化算法
本章将详细介绍本文提出的免疫遗传影响力最大化算法。如图2,算法主要利用免疫算法框架快速地迭代出网络中最具有影响力的节点。对记忆库采用启发式策略加速算法的进化。

Fig.2 Framework of IGIM algorithm图2 免疫遗传影响力最大化算法框架
4.1 编码方式
在IGIM 算法中,群体中每一个抗体Xi采用实数值编码。抗体Xi=(xi1,xi2,…,xiK)表示由K个节点组成一个集合,每一个抗体也代表着影响力最大化问题的可行解。举个例子,假设给定影响力节点集数目K=3,那么抗体Xi=(33,100,1)代表抗体由节点编号33、100 和1 的节点组成的集合,这里需要注意的是每一个抗体不能出现重复节点编号。
4.2 适应值函数
受到Zhang 等人工作启发,发现在计算节点集影响力概率,随着阶级增大而逐渐呈现收敛状态。如图1,根据容斥定理计算节点5 被激活概率为π5=0.064 7,评估节点1 的影响力可以忽略不计二阶邻居节点5 的激活概率,而只关注节点1 直接邻居节点2、4 和3。因此在IC 传播模型下,本文提出有效的局部容斥(local inclusion exclusion,LIE)概率解适应值函数,通过计算节点集的一阶邻居节点的激活概率,近似估计节点集的影响力。给定一个网络G=(V,E)和种子节点集S,每一个节点的激活概率πv,局部容斥概率解影响力评价函数LIE 可以定义为:

其中,v∈表示种子节点集的一阶非激活邻居节点,π表示激活概率向量,其元素是节点激活概率。适应值函数伪代码在算法1 中给出。
算法1局部容斥概率解LIE

4.3 抗体期望繁殖概率
在免疫遗传算法中,引入抗体期望繁殖概率是为了鼓励与抗原具有高亲和力的抗体,并且对高浓度抗体进行抑制。在本文中,与抗原的亲和力函数采用适应值函数。抗体浓度与抗体之间的相似度有关。抗体之间相似度计算,采用R 位连续匹配算法。由于抗体编码在影响力评估与编码之间的顺序无关,因此抗体之间相似度可表示为:

其中,li,j表示抗体i与抗体j相同的编码个数;K表示抗体的长度。因此抗体浓度ci即与抗体i相似的抗体所占群体的比例,可定义为:

其中,n为抗体的总数,,T为一个阈值。
抗体的期望繁殖概率是由抗体的适应值和抗体浓度共同决定的,因此抗体的期望繁殖率可定义为:

通过免疫机制进行个体选择作为父本与群体中其他个体做两点交叉操作,变异进化出优质可行解并更新种群。
4.4 IGIM 算法
IGIM 算法基本思想是利用免疫机制融入传统遗传算法,并集成局部容斥概率解适应值函数进行优化,寻找网络中最具有影响力的节点集。如图2,IGIM 算法主要包括抗体编码初始化和进化两个阶段。具体描述如算法2 所示。
算法2IGIM 算法

算法初始化阶段(行3),为获得较好的种群多样性,对每个抗体采用随机策略从记忆库当中选取K个节点进行抗体编码。算法进化阶段(行4~行16),采用传统两点交叉算子和变异算子。在两种操作中,均使用记忆库提供高质量节点进行抗体中元素替换,加速算法快速寻优到最优可行解。
根据算法2,对IGIM 算法进行时间复杂度分析。在算法中需要对产生的新节点集进行局部容斥概率解的影响力评估,根据算法1 得出影响力评估函数时间复杂度为。算法初始化阶段(行1、行2)时间复杂度为。算法的迭代进化阶段(行4~行16)时间复杂度为O(n2KImax)+O(2nmKImax)+O(mnK2Imax)。因此算法IGIM 在最差情况下,时间复杂度为Imax)。其中n表示种群的大小,K为种子节点集的数量,Imax表示算法的迭代进化次数,表示为网络节点的平均度。
5 实验与结果
为验证提出的IGIM 算法性能,本文选取4 个真实的数据集进行实验结果对比和分析,并验证所提出局部容斥概率解影响力评估性能。下面是对实验的详细设置。
5.1 数据集
本文选择4 个真实学术合作网络数据集Net-Science[21]、NetGRQC[22]、NetHEPT 和NetPHY[10]。这4个数据集描述的是不同领域科学家之间科研合作网络,节点表示科研人员,边表示科研合作人员之间的学术成果或出版刊物,均为无向图。4 个数据集的详细信息如表1 所示。
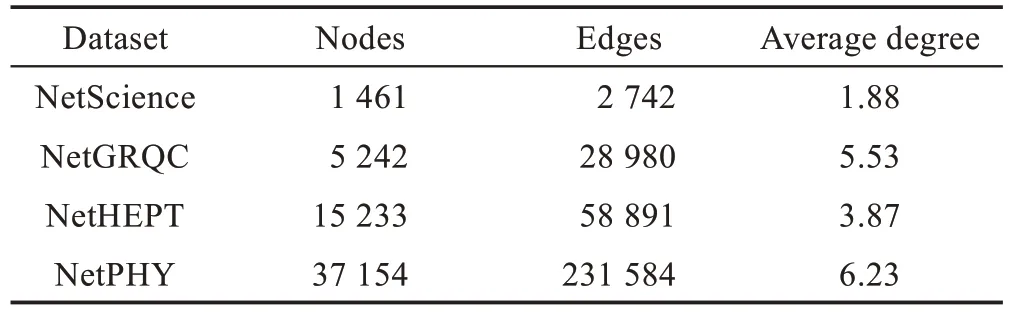
Table 1 4 real-world social networks表1 4 个真实社会网络
5.2 对比算法与实验设置
在对比实验中,选择CELF、SAEDV、DPSO、DDSE和Random 共5 个算法进行对比。其中CELF 算法是基于子模性质对贪心算法的改进,在传播影响范围上与贪心算法的性能一致。SAEDV、DPSO 和DDSE算法都采用智能优化算法解决影响力最大化问题,在时间效率上都是非常先进的算法。Random 算法是基线对比算法。
本文是在IC模型下运行10 000次Monte-Carlo模拟评估每个算法的种子节点集影响扩展。除CELF算法以外,其他所有算法均独立运行30 次取平均结果。SAEDV 算法参数设定:初始温度T0=500 000,最终温度Tf=8 000,内循环q=200,温度下降梯度ΔT=2 000。IGIM 算法实验参数是根据实验优化所得,如表2 所示。其他对比算法实验参数均使用各自论文中实验参数。
为了方便实验分析,传播概率p设置为0.01,与先前的研究一致[19]。所有算法都使用Java 语言编写。所有实验均在2.3 GHz Intel Core i5 和16.0 GB内存的PC 上运行。

Table 2 Parameters in IGIM algorithm表2 IGIM 算法参数
5.3 实验结果与分析
评价影响力最大化算法通常使用影响传播范围和运行时间这两个常规指标。传播影响范围为影响力最大化算法寻找到的种子节点集在特定传播模型下的影响节点数目;运行时间即算法寻找到种子节点集所花费的时间。
5.3.1 影响力评估函数对比
本文提出了局部容斥概率解影响力评估函数,为了验证该函数的性能,取IGIM 算法在4 个数据集上分别寻找到的30 个种子节点,使用局部容斥LIE、容斥IE 和蒙特卡洛MC 模拟分别计算种子节点集影响力估计和运行时间。
如图3(a)实验结果,在4 个数据集上,局部容斥概率解非常逼近MC 模拟的性能。在NetPHY 数据集上,LIE 的评估性能稍逊于MC 模拟,这可解释为在大型的复杂网络上,局部的影响力估计会丢失一部分传播信息。如图3(b)实验结果,在大数据集NetPHY上LIE 运行时间比其他两种方法快大约3 个数量级。因此,本文所提出的局部容斥概率解影响力评价函数能够高效准确地对节点集影响力作出近似估计。
5.3.2 传播影响范围对比
图4 实验结果显示6 个算法在不同种子节点集大小、4个数据集上影响传播范围的变化情况。根据图4实验结果得知,IGIM 算法和CELF 算法在4 个数据集上具有极其相近的性能,超过其他对比算法。其中,SAEDV 仅次于本文算法IGIM。数据集NetScience和NetHEPT 相对于其他两个数据集较为稀疏,因此在传播范围上,CELF、IGIM、SAEDV 和DDSE 之间的性能差距不是很大。

Fig.3 Comparison of performance of influence evaluation functions on 4 datasets图3 影响力评估函数在4 个数据集上的性能对比
在种子集大小K=30 的情况下,IGIM在NetGRQC数据集上传播精度分别优于SAEDV、DDSE 和DPSO算法2.18%、4.13%和11.09%,在NetPHY 数据集中分别是1.5%、7.87%和9.92%。DPSO 在4 个数据集上表现仅次于DDSE 算法,尤其在NetPHY 数据集上,随着K值不断增大,DPSO 和DDSE 算法的性能在不断下降。可以分析得出,在大型复杂网络上度中心性启发式策略存在一定的局限性,仅有节点的局部拓扑结构信息。Random 算法随机组合网络中的节点,在4 个数据集上表现是最差的。
5.3.3 运行时间对比
为验证IGIM 算法的时间效率,图5给出种子节点集大小为30的各个算法运行时间。在4个数据集上,IGIM 算法时间效率优于DDSE、DPSO 和SAEDV 算法。在数据集NetPHY 上,IGIM 算法比DDSE、DPSO和SAEDV 算法快大约20.38%、74.62%和79.71%。SAEDV 算法因为要万次的迭代进化,因此运行时间要差于利用启发式策略加速的DDSE 和DPSO 算法。DPSO 和DDSE 算法分别使用了度中心性和度下降启发式策略,但是收敛速度要次于算法IGIM。

Fig.4 Influence spread on 4 datasets under independent cascade model图4 独立级联模型下4 个数据集上的传播影响范围

Fig.5 Comparisons of running time of different algorithms图5 不同算法之间运行时间对比
在4 个数据集上,CELF 算法运行需要通过MC模拟寻找到最具有边际影响力的节点,时间开销很大,因此效果最差。Random 算法随机组合生成种子节点集,时间效率虽然是最好的,但在传播影响力范围上的性能是最差的。
6 结束语
本文提出局部容斥概率解评价函数,可以有效快速地估计节点集的近似影响扩散。在IGIM 算法中,采用LIE 函数进行单个节点影响力计算并选择优秀节点构造记忆库,用来加速算法进化过程。在传播影响范围和运行时间两个指标上,算法在4 个真实数据集上对比实验数据表明,IGIM 算法都有优秀的表现,在传播范围和时间复杂度取得良好的平衡。在未来工作中,将继续探究IGIM 算法在结合文本语意信息的传播模型上的应用。
