对第一类换元积分法的研究与改进

陈 思 闫伟杰

（浙江同济科技职业学院，浙江 杭州311231）

1 概述

第一类换元积分法（也称凑微分法）是在高等数学学习过程中遇到的第一种积分方法，也是在积分计算题目中运用最广泛的一种方法。其思路是通过引进中间变量作变量替换，使原式结构变得更加简单，从而解决较为复杂的不定积分问题。常规的换元方法存在选取合适的中间变量难、凑微分时容易配错常数等问题，尤其是对于数学基础薄弱、微分公式运用不够灵活的学生，在做题过程中特别容易出错，从而产生畏难情绪。针对这个问题，本文提出了一种更为简单且不容易出错的换元方法，避开了凑微分时配常数的计算，降低了换元难度。

2 第一类换元积分的常规解法

第一类换元积分法是复合函数链式法则的逆推。若F（x）是f（x）的一个原函数：

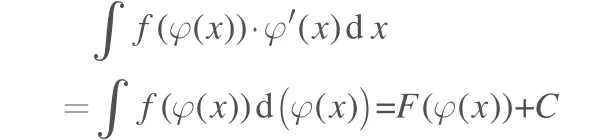
其中被积函数是以f（φ（x））·φ'（x）出现的，但解决实际题目时，很少会直接给出这样的结构，所以选取一个合适的中间变量u=φ（x），是解决题目的关键。

常规解题思路为：

（1）观察：选取合适的中间变量u=φ（x）；

（2）求微分：φ'（x）dx=d（φ（x））；

（3）换元：将原式中的φ'（x）dx 换为d（φ（x）），或是原式中的c·φ'（x）dx 换为c·d（φ（x）），其中c 为常数；

（4）求积分：将简化过的式子运用合适的积分公式，求出原函数。

下面以两道例题来说明：

（1）观察：选取u=1+x3；

（2）求微分：3x2dx=d（1+x3）；

（4）求积分：

（1）观察：选取u=3lnx+1；

（4）求积分：

从上面两道例题中，不难发现解题过程中存在两个难点：

第一，换元时，若题目中包含c·φ'（x）dx，需要进行常数的计算。学生经常在此处漏算或错算常数，考试中这常常是该类题目的主要失分点；

3 改进的换元方法——直接对被积变量进行换元求解

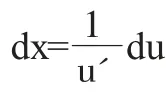
步骤如下：

（1）观察：选取合适的中间变量u=φ（x）；

（3）求积分：将简化过的式子运用合适的积分公式，求出原函数。

前面两个例子用直接对被积变量进行换元求解如下：

（1）观察：选取u=3lnx+1；

（2）计算微分公式并直接换元

（1）观察：选取u=3lnx+1；

（3）求积分：

4 结论