拱形张弦结构的优化设计

邹 荣， 张涵坤， 张佳庆

(1. 武汉正华建筑设计有限公司， 湖北 武汉 430090； 2. 新城控股集团股份有限公司， 上海 200333；3. 华中科技大学 土木工程与力学学院， 湖北 武汉 430074)

拱形张弦结构由上弦拱梁、拉杆和上凸式预应力拉索相互连接组成(如图1)，采用一端简支、一端滑动的支座。与传统张弦结构[1]相比，拱形张弦结构保留了自平衡特性，将传统张弦结构下垂的悬索变为上凸拉索，这样拱的矢高更大，同时大幅提升了建筑室内空间使用效率；连接上弦刚性构件与拉索的撑杆由压杆变为拉杆，避免由于长细比限制而使其截面尺寸过大，并降低拱结构的弯矩峰值。拱形张弦结构较传统张弦结构拥有更大的建筑室内净高、更高效的空间使用效率，内部视觉明快，目前已较多应用于大型工业厂房、物流仓储等建筑的屋盖结构。拱形张弦结构优美的造型、合理的结构形式以及高效的空间利用率使其具有广泛的应用前景。

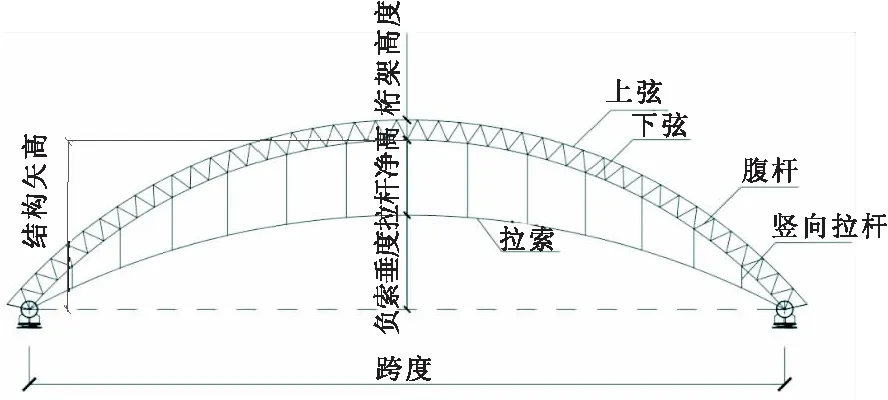
图1 拱形张弦结构的组成与设计参数

目前，国内对张弦结构的研究主要集中在传统的单、双向张弦梁上，陈楠[2]采用伽辽金法推导出了拱形张弦结构在各荷载状态下位移、内力的解析公式，并进行静力、动力性能实验，验证了理论公式的正确性。吴捷[3]对空间双向张弦梁结构采用零阶与一阶相结合的优化算法，提出了两步三级的优化设计方法，分别对结构形状、预应力和各构件截面尺寸等不同性质参数进行分层优化。蔡建国等[4]对新广州站工程三向张弦桁架进行形状参数与构件截面的综合优化，利用一阶优化方法，通过引入罚函数进行最小化求解，并给出最佳矢跨比、垂跨比，及矢高与垂度比值的最经济比值范围。以上研究主要针对传统的拉索下垂式张弦体系，而传统的张弦结构[5]对室内使用净高不利，新型的拱形张弦结构设计需要深入研究。

本文通过对拱形张弦结构进行非线性静力分析，研究了结构矢跨比[6]、高跨比、桁架高度、拉杆间距、拉索预应力对拱形张弦力学性能指标的影响；研究了结构矢高与拉杆净高的比值即矢高比在不同设计参数下的最经济取值范围，为结构设计提供参考建议。

1 拱形张弦结构的有限元模型

本文采用有限元软件SAP2000对拱形张弦结构进行计算，采用以下基本假设：材料处于弹性状态；拉索单元只能承受拉力；拉索单元与拉杆之间不会发生滑动，采用铰接固定；所有荷载均作用在拱桁架的上弦节点与檩条上，弦杆与腹杆刚接。

拱形张弦结构关键几何参数为：结构跨度L、拱矢高fa、负索垂度fc、拉杆净高fs(fs=fa-fc)、桁架高度H。

2 拱形张弦结构的参数分析

根据《空间网格结构技术规程》[7]，选取跨度为120 m、各榀间距为15 m的拱形张弦结构。以单榀张弦拱作为研究对象，其几何参数为：矢高27 m(矢跨比为1/4.44)，拉杆净高13 m(高跨比为1/9.2)，索负垂度14 m；桁架截面为高度与宽度均为3.2 m(结构跨度的1/10)的倒三角形截面(见图2)。拉杆采用竖向拉杆形式，共13根。结构一端为固定铰支座，另一端为可滑动铰支。

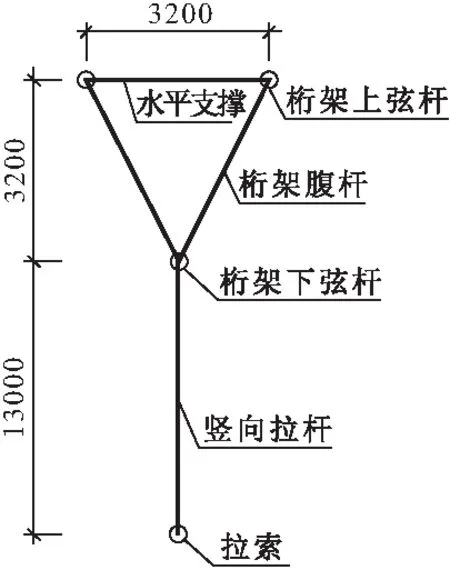
图2 拱形张弦结构跨中截面/mm

结构恒荷载为屋面板自重及檩条、支撑、各类管线设备的自重，合计取1.2 kN/m2；屋面活荷载为雪荷载等，取0.5 kN/m2；将恒载、活载均等效为作用在上弦杆上的均布荷载。选取竖直向上的方向为竖向位移的正方向，远离结构的方向为水平位移的正方向。构件的材料参数及截面尺寸见表1，2。

表1 构件的材料参数

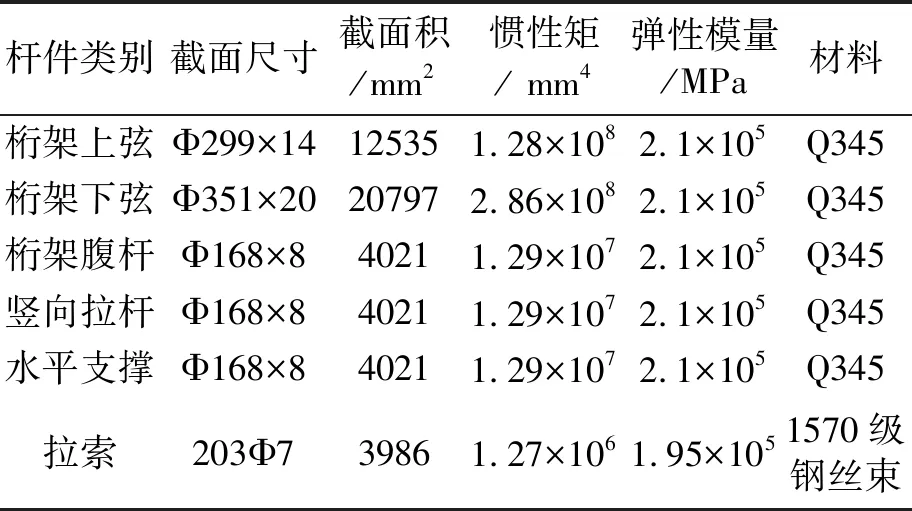
表2 构件的截面尺寸

在结构计算分析中共考虑四种荷载工况，分别为：工况一：杆件自重+预应力；工况二：杆件自重+预应力+屋面恒载；工况三：杆件自重+预应力+屋面恒载+活载；工况四：杆件自重+预应力+屋面恒载+1.4风荷载。当结构采用高重度的上弦杆或屋面板时，工况四中的屋面恒荷载可抵消掉方向向上的风吸力影响，故选取工况三作为最不利工况，并将荷载分成三级施加，模拟施工过程中的荷载变化状况，即LOAD0=杆件自重+预应力；LOAD1=杆件自重+预应力+1/2(屋面恒载+活载)；LOAD2=杆件自重+预应力+屋面恒载+活载。

选取拱形张弦结构的跨中竖向变形、滑动支座水平位移，以及上、下弦杆等关键杆件的内力作为分析对比指标。对钢拉索施加温度荷载[8](降温)使其收缩，由结构的约束限制使拉索产生预拉力。初始温度荷载的估算公式为：

式中：P为设计预应力值；α为钢索材料的线膨胀系数；A为钢索截面面积；E为钢索弹性模量。

2.1 初始预应力

选取初始预应力值依次为0，300，600，900，1200 kN，其余几何、荷载参数均保持不变。跨中竖向变形、水平位移和上、下弦杆内力随初始预应力取值的变化曲线见图3，其中弦杆内力变化曲线为在工况三荷载作用下改变初始预应力值获得。

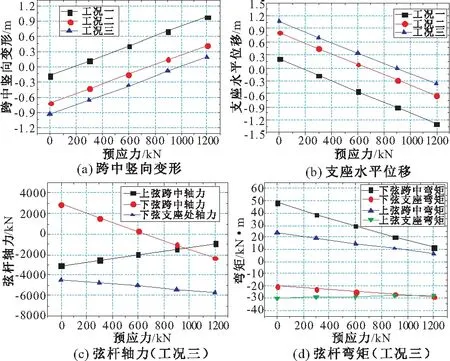
图3 结构位移、弦杆内力与预应力的关系曲线

对图3分析可知，对拉索施加适当的初始预应力可使拱桁架、拉索、拉杆协同受力，对降低拱桁架的跨中弯矩和竖向变形、支座水平位移的效果尤为明显，但施加过大的预应力会增大下弦杆的内力负担。由于拱形张弦结构的矢跨比较大，支座水平位移的变化更加敏感，因此在实际设计中，合理预应力应综合考虑控制支座水平位移与拱桁架的内力，并以前者为主。

具体步骤为：首先计算结构在工况四[10](杆件自重+屋面恒载+1.4风荷载)作用下的内力，确保拉索在风吸力作用下不会发生松弛[9]。从控制拱桁架内力的角度出发，合理预应力为使最大竖向荷载作用下(工况三)的拱桁架弯矩值最小时的预应力值；从控制支座水平位移的角度出发，合理预应力应使工况二与工况三分别作用下的支座水平位移等值反向，即为平衡杆件自重+屋面恒载+ 0.5活载作用下的支座水平位移时的预应力值。

表3，4对上述两种预应力取值方案进行了比选。

表3 初始预应力取值方案

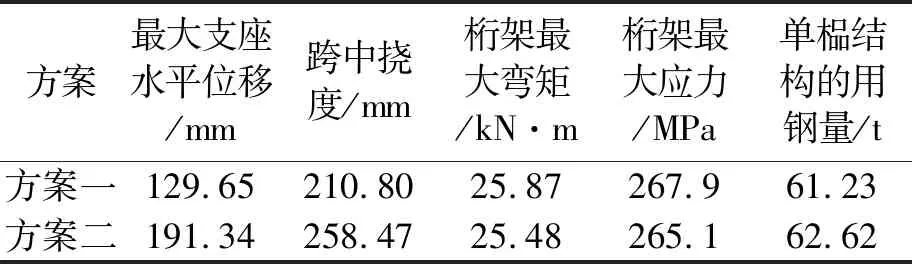
表4 方案比选

方案一相比较于方案二桁架支座水平位移减少了61.69 mm，跨中挠度减少了47.67 mm，而桁架最大弯矩值相差不大，因此方案一的预应力值作为本算例的最佳预应力的初步取值，即774.8 kN。

2.2 桁架截面高度

依次改变拱桁架截面高度为2.4，2.8，3.2，3.6，4.0 m，改变范围为跨度的1/50～1/30。在结构自重产生的索拉力基础上施加550 kN的预应力，其余几何、荷载参数均保持不变。在最不利工况三的分级荷载LOAD0，LOAD1，LOAD2作用下，桁架高度改变时结构跨中竖向变形、支座水平位移随桁架截面高度的变化曲线以及弦杆内力单独在LOAD2作用下的变化曲线见图4。

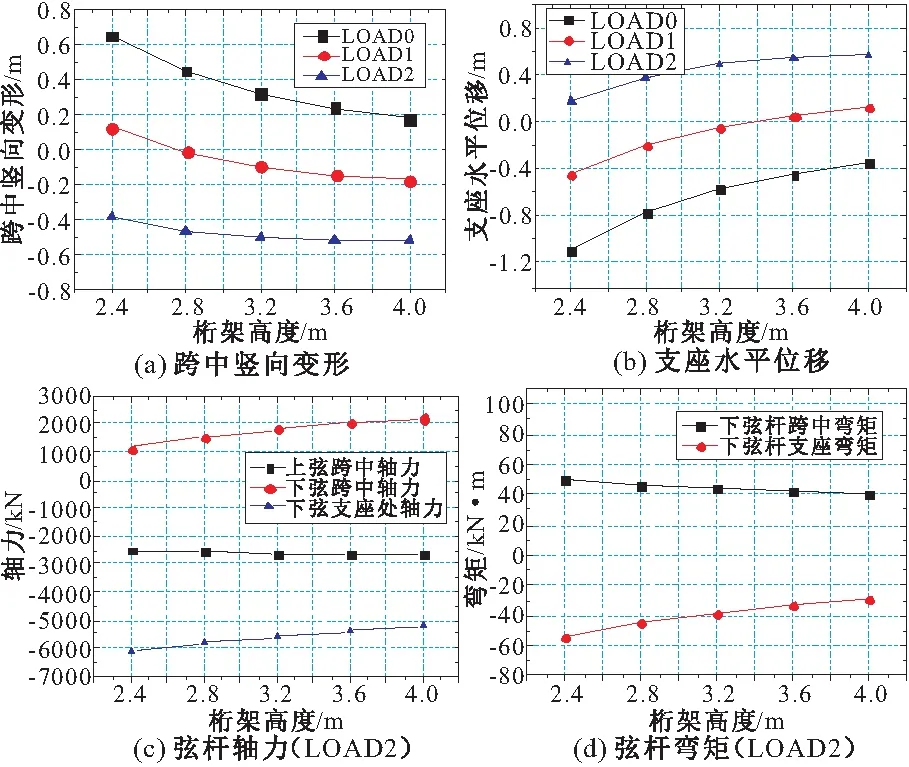
图4 结构位移、弦杆内力与桁架高度的关系曲线

由图4可见，结构各构件的变形、内力与桁架高度之间基本呈线性关系。增大桁架截面高度会增加结构用钢量，但能显著提升结构刚度，降低竖向变形值，减小支座水平位移绝对值，除上弦杆内力负担增大，其余构件受力状况均得到改善。当结构位移并非主要控制对象时，从节省用钢量的设计角度出发，桁架高度建议取跨度的1/40～1/35。

2.3 拉杆间距

将拉杆间距由40 m减小至7.1 m，其余几何、荷载参数均保持不变。在分级荷载LOAD0，LOAD1，LOAD2作用下，结构的跨中竖向变形、水平位移、拉杆轴力随拉杆间距的变化曲线以及弦杆内力单独在LOAD2作用下的变化曲线见图5。

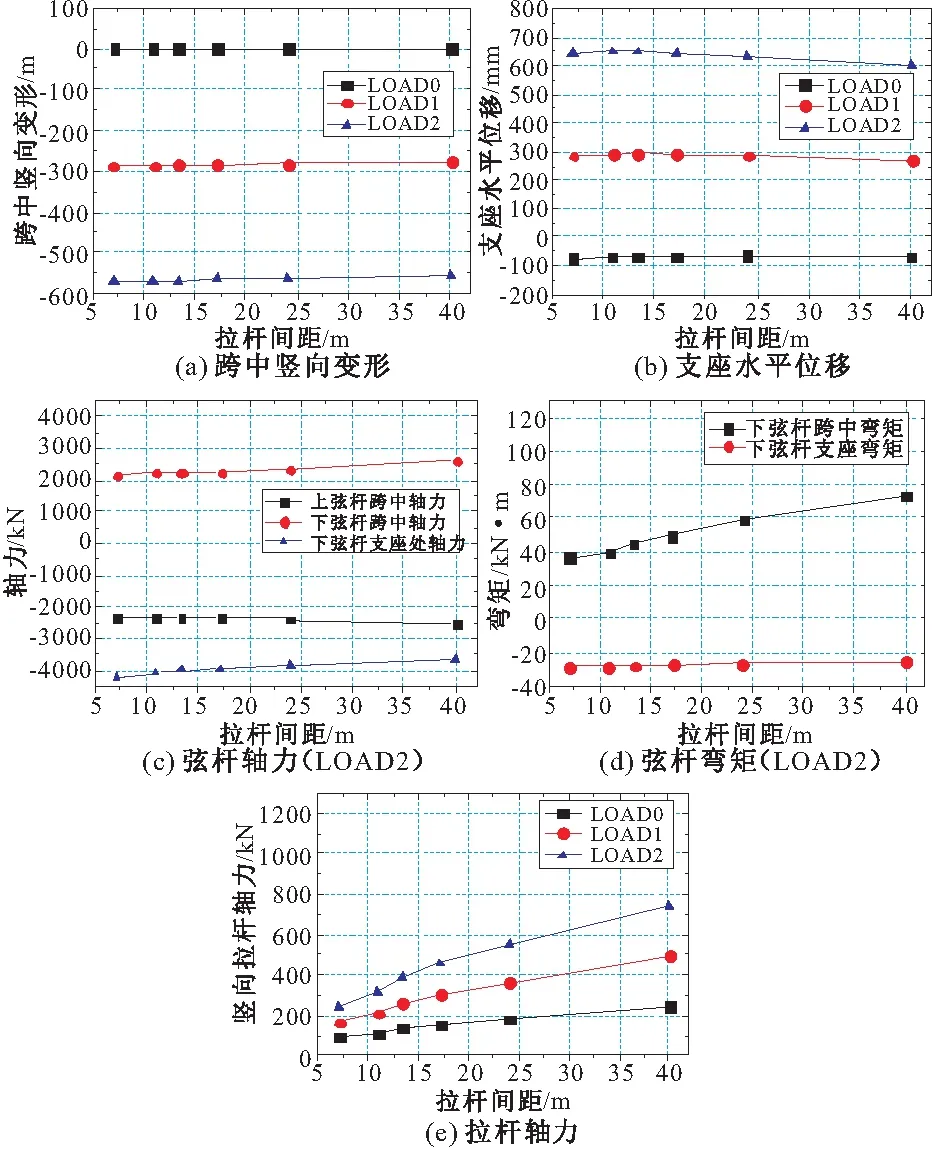
图5 结构位移、弦杆内力与拉杆间距的关系曲线

由图5可见，减小拉杆间距主要降低了拱桁架下弦的弯矩峰值及拉杆自身的轴向拉力。拉杆间距减小到一定值之后，对结构的内力分布、位移影响较小。因此建议在实际设计中，将刚度作为主要控制对象，避免其发生失稳。采用竖向拉杆时，平均间距取10～15 m为宜。

2.4 结构矢高与拉杆净高

选取结构矢高依次为18，22.5，27，31.5，36 m，采用竖向拉杆形式，拉杆净高固定为13 m，施加550 kN的预应力，其余几何、荷载参数均保持不变。在LOAD0，LOAD1，LOAD2工况下，结构的跨中竖向变形、水平位移随矢跨比的变化曲线以及弦杆内力单独在LOAD2作用下的变化曲线见图6。

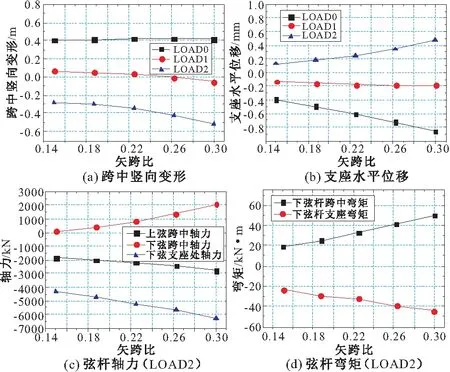
图6 结构位移、弦杆内力与结构矢跨比的关系曲线

选取拉杆净高依次为12，13，14，15 m，即高跨比为0.1～0.125，结构矢高固定为31.5 m，其余几何、荷载参数均保持不变。在LOAD0，LOAD1，LOAD2工况下，结构的跨中竖向变形、水平位移随高跨比的变化曲线以及弦杆内力单独在LOAD2作用下的变化曲线见图7。

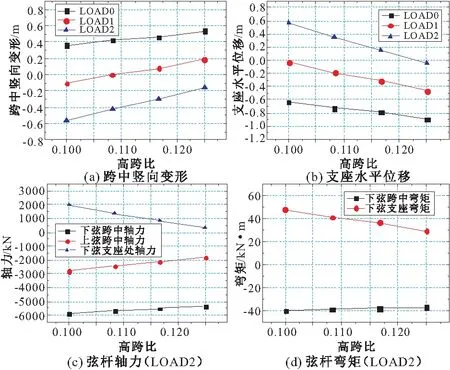
图7 结构位移、弦杆内力与高跨比的关系曲线

如图6，7所示，对于拱形张弦结构，增大高跨比可以提升结构竖向刚度，改善结构整体受力性能；增大矢跨比可以提升建筑内部的使用空间，但是会增大结构各构件的内力负担，增大结构变形，当矢跨比大于0.23后，结构内力会快速增长。因此，在结构设计时，需在满足建筑要求的情况下，找到相对经济的矢高与拉杆净高的比值即矢高比。

2.5 结构矢高与拉杆净高的最经济比值

拱形张弦结构的结构矢高与拉杆净高的最经济比值表示使结构在进行优化设计后用钢量最小所对应的值，它需要根据不同的设计条件来确定，例如建筑要求的负索垂度fc(净空高度)、结构的跨度、屋盖荷载大小、拱桁架截面高度、屋盖结构是否悬挂吊车等因素共同决定。通过研究拱形张弦结构的矢高与拉杆净高的最经济比值，可以大幅提高结构形状优化的效率，为结构设计带来便利。

对跨度为120，110，100，90，80 m的拱形张弦结构模型分别按负索垂度与跨度的比值fc/L为0.16，0.2，0.24的净高要求按满应力准则进行截面优化设计。得到不同跨度、不同垂跨比，以及采用不同屋面板的矢高比最经济值，可作为设计参考，具体见表5。其中，采用的轻型、重型屋面板重度分别为0.55，1.2 kN/m2。

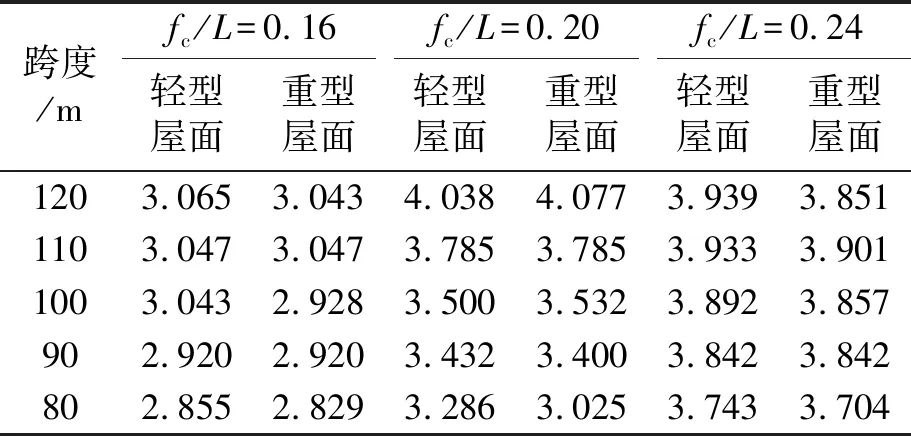
表5 不同跨度、垂跨比下的矢高比最经济值

从表5可知，跨度或垂跨比增大均会导致结构矢高与拉杆净高的最经济比值变大。在结构设计中，可根据上表采用插值法确定不同跨度、垂跨比模型的最经济比值，且误差较小。

3 结 论

本文通过对拱形张弦结构进行非线性静力分析，研究了拉索预应力、桁架高度、拉杆间距、矢跨比、高跨比、矢高比等关键参数对拱形张弦结构力学性能与经济指标的影响，主要结论如下：

(1)对拉索施加适当的初始预应力可使拱桁架、拉索、拉杆协同受力，对降低拱桁架的跨中弯矩和竖向变形、支座水平位移的效果尤为明显，但施加过大的预应力会增大下弦杆的内力负担。由于拱形张弦结构的矢跨比较大，支座水平位移的变化更加敏感，因此在实际设计中，合理预应力应综合考虑控制支座水平位移与拱桁架的内力，并以前者为主。

(2)当结构位移并非主要控制对象时，从节省用钢量的设计角度出发，桁架高度建议取跨度的1/40～1/35，增大桁架截面高度会增加结构用钢量，但能显著提升结构刚度，降低竖向变形值、减小支座水平位移绝对值，除上弦杆内力负担增大，其余构件受力状况均得到改善。

(3)采用竖向拉杆时，平均间距取10～15 m为宜。减小拉杆间距主要降低了拱桁架下弦的弯矩峰值及拉杆自身的轴向拉力，且拉杆间距减小到一定值之后，对结构的内力分布、位移影响较小。因此建议在实际设计中，将刚度作为主要控制对象，避免其发生失稳。

(4)对于拱形张弦结构，增大高跨比可以提升结构竖向刚度，改善结构整体受力性能；增大矢跨比可以提升建筑内部的使用空间，但是会使结构各构件承受一定的内力负担，增大结构变形。当矢跨比大于0.23后，结构内力会快速增长。

(5)不同跨度、不同设计净高要求、不同荷载下的矢高与拉杆净高的最经济值在2.8～4.1之间。采用0.55 kN/m2的轻型屋面板与1.2 kN/m2的重型屋面板所对应最经济值的差别基本在15%以内，不受控制挠度值的影响，初始设计时的矢高比最经济值可参考表5数据通过插值法确定。