模糊多核一类支持向量机
2020-05-12张庆朔张长伦王恒友
张庆朔, 何 强, 张长伦,2, 王恒友
(1.北京建筑大学 理学院, 北京 100044; 2.北京建筑大学 北京未来城市设计高精尖创新中心, 北京 100044)
支持向量机(SVM)[1-2]是一种按监督学习的方式对数据进行有效分类的算法,它更适合处理两类分类问题. 但是现实中存在许多一类分类问题,或者类别极不平衡的数据的分类问题,比如异常检测问题[3],只有一个类的数据构成输入空间,异常点极少或不容易获得. 使用经典支持向量机算法处理这种问题时,往往效果不理想. 但是支持向量机因其可实现结构风险最小化[4],找到全局最优以及泛化能力强受到学者的广泛关注,展开了基于支持向量机的一分类问题的研究——对给定的训练数据设计一个边界,使目标类数据落在边界内. 基于这种思想,提出了两种基于支持向量机的一分类学习算法,即支持向量数据描述(SVDD)[5]和一类支持向量机(OCSVM)[6]. 支持向量数据描述的主要思想是找到一个半径最小的超球,可以包含所有的目标数据,处于超球外的数据即为异常数据. OCSVM的主要思想在特征空间中找到一个超平面,将目标数据与特征空间的原点以最大间隔分开,与原点在同一侧的数据即可判断为异常数据. 本文主要研究用OCSVM处理类别不平衡数据的分类问题.
一类支持向量机继承了支持向量机的优点,但是也保留了其缺点,需要使用核函数将数据映射到特征空间中,将原始空间中的非线性分类问题转化为特征空间的线性可分问题,面临核函数核参数的选择难题. 不同的核函数刻画数据间信息的侧重点不同,决定着分类器性能的优劣. 常用的核函数有:线性核函数;多项式核函数;高斯核函数. 目前,多核学习[7-11]是核方法方面的研究热点,用多个核函数的组合代替单一核核函数,在分类算法中取得了不错的效果. 多个核函数形成的组合核比单一核刻画数据间相似性的能力更好,更能保留原始数据的特征,尤其是对复杂数据的刻画能力更好,克服了核选择的难题.
SVM训练过程中易受噪音的影响,OCSVM也有同样的问题. 当前OCSVM解决这一问题主要是对训练样本进行加权处理,样本权重的计算方法结合了样本的几何信息. 2014年,CHA M等[12]提出一种基于原始空间中样本的局部密度加权的方法,权重的计算依赖于该样本与其第k个近邻的距离与所有样本与其第k个近邻的距离的最大值的比值,当比值越小时,权重越大,即位于密度大的区域的样本点具有较大的权重. 2016年,YANG J等[13]提出了一种类似的权重计算方法,样本的权重大小依赖于该样本到数据中心的距离与所有样本到数据中心的距离的最大值的比值,当比值越接近1时,分配的权重越小,即距离样本中心越远,权重越小. 2016年,HOU T等[14]提出一种结合样本的局部密度和样本点到样本中心的距离计算权重的方法. 同年,ZHU F等[15]提出了一种用样本k近邻的余弦和描述样本的几何分布,从而构造样本权重的方法,主要思想是使分布在数据集边界处的样本具有较小的权重. 上述方法都是依据样本的重要程度,对样本分配权重,使其对分类边界产生不同的贡献. 模糊粗糙集[16]是一种处理不确定性的数学工具,可以更好地发现隐藏在数据间的信息. 通过模糊粗糙集,依据特征与类别的一致性程度,能够为每个训练样本赋予一个模糊隶属度,可以有效表示其隶属于目标类的程度. 受加权和模糊粗糙集思想的启发,为同时解决OCSVM中核选择难题和对噪音数据敏感问题,将模糊隶属度引入到多核一类支持向量机(MKOCSVM)中,使重要的样本在训练过程中发挥更大的作用,淡化不重要的样本点或噪音的影响,以克服MKOCSVM对噪音敏感问题.
本文的主要工作如下:
1) 将模糊隶属度引入到多核一类支持向量机,提出模糊多核一类支持向量机(FMKOCSVM),同时解决一类支持向量机的核选择难题和鲁棒性差的问题.
2) 基于模糊粗糙集理论,用CHEN D等[17]提出的模糊隶属度函数为每个训练样本确定模糊隶属度,更有效地减小噪音数据对分类边界的影响.
3) 多核学习中组合核采用线性加权的方式构造,核权重通过最大化组合核和理想核的相似性计算获得[18],获得的组合核更充分地利用了数据的信息.
4) 在人工数据集和标准数据集上,对比OCSVM、MKOCSVM、FMKOCSVM三种算法的在噪音环境下的性能,本文提出的FMKOCSVM算法均获得最佳的结果.
1 相关知识
1.1 一类支持向量机
相较于经典SVM,OCSVM适用于处理数据类别不平衡或单类分类问题,其主要思想是首先通过非线性映射将数据从原始空间映射到特征空间,并将特征空间的原点作为异常点的代表,在特征空间中寻找一个最优分类超平面——可以将正常数据的像与原点以最大间隔分开.
设有样本数据{x1,x2,…,xl}∈Rn,l是样本数量,φ(x)是将样本映射到特征空间的函数,ω、ρ表示特征空间中分离超平面的法向量和偏移量,分离超平面的表达式为ωTφ(x)-ρ=0. 目标是最大化分离超平面与原点之间的距离,则OCSVM需要求解以下优化问题[5]:

(1)
式中ξi是松弛变量,表示允许离群点存在,v是控制离群点数量上限和全部支持向量数量下限的参数.
利用Lagrange乘子法,可得上述优化问题的对偶问题,即:

(2)
其中αi是样本xi对应的拉格朗日系数, 核函数k(xi,xj)=〈φ(xi),φ(xj)〉,代替了特征空间中的内积.

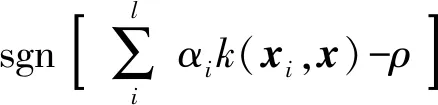
(3)
对于给定的一个测试样本,代入式(3)后,当决策值为+1时,该样本被判别为正常点;当决策值为-1时,该样本被判别为异常点.
1.2 多核学习
分类算法中的核函数核参数的选取,对分类器的性能有着至关重要的影响,目前普遍是靠经验试算或者交叉验证. 交叉验证的本质就是一种枚举法并受选定的参数定义域的影响,与经验试算一样需要消耗大量的时间,且不一定能获得最佳的分类性能.
对于解决SVM中核函数核参数的选择问题,用组合核代替单一核的思想取得了不错的进展. 近几年有许多关于核组合方法的研究,现已形成一个新的研究领域,即多核学习. 在多核学习的研究中,关于组合核的构成方法,常用的有:
1) 线性组合的方法[19]. 将多个基本核线性组合的结果作为组合核. 其中有:
a)直接求和方式:
(4)
b)加权求和方式:
(5)
c)多项式加权扩展方式:
(6)
其中,kp(x,z)是k(x,z)的多项式扩展.
2) 非线性组合的方法[20]. 如乘积:
(7)
2 模糊多核OCSVM
OCSVM普遍面临核选择难题与噪音数据敏感问题,为同时解决这两个问题,本文将模糊隶属度引入到MKOCSVM模型中,期望提高MKOCSVM的鲁棒性, MKOCSVM模型如下式:

(8)
与式(1)相比,特征空间中的内积由组合核函数计算,即kη(xi,xj)=〈φη(xi),φη(xj)〉,映射函数φη(x)发生改变. 本文中采用的组合核是线性加权的组合方式,即式(5),核权重是通过最大化组合核和理想核之间的相似性优化[18]获得.D为训练集,理想核的定义是yyT,y=(y1,y2,…,yl)T,yi∈{1},i=1,2,…,l,表示训练集的标签. 求核权重的优化问题如下式:

∑Pm=1ηmKm,yyTF∑Pm=1ηmKm,∑Pm=1ηmKmF〈yyT,yyT〉F=

(9)

(10)
根据式(9)的性质. 可选择λ=1,为避免过拟合,对η添加约束,式(9)最终等价于:

(11)

模糊多核一类支持向量机的优化问题为:

(12)
对于类别确定性高,即模糊隶属度si大的训练样本,对其分类错误的惩罚加大;对于模糊隶属度小,即不重要的训练样本或噪声数据,减小其分类错误的惩罚,淡化其对决策边界的影响. 使用模糊粗糙集下近似算子作为某目标类A样本的模糊隶属度. 对于目标样本xi,其属于目标类A的隶属度为:
(13)
引入Lagrange乘子αi,γi后,上述优化问题(12)对应的Lagrange函数为:

(14)
L(ωη,ξ,ρ,α,γ)对ωη,ξ,ρ求偏导并令其为零,可以得到:
(15)
将式(15)代入式(12),可以得到FMKOCSVM的对偶问题为:
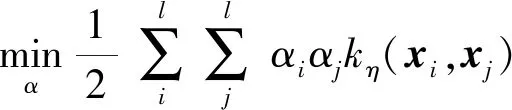
(16)
与OCSVM模型的对偶问题相比,只有αi的上界不同. 得到的决策函数为:
(17)
本文提出的模糊多核一类支持向量机算法主要过程见表1.

表1 模糊多核一类支持向量机Tab.1 Fuzzy multiple kernel one-class support vector machine
3 实验仿真
本节中,在MATLAB2015b平台上进行仿真实验,对比FMKOCSVM与MKOCSVM、OCSVM三种算法在噪音环境中的分类性能. 所有实验均在一台配置为Core i5- 3230+8G RAM的计算机进行,操作系统为Windows 10.
为了验证所提出模型的可行性,首先在人工数据集上对三种算法的分类性能进行了可视化. 然后在16个标准数据集上对三种算法进行了实验比较,进一步验证所提出模型的有效性. 所用的性能评价指标为训练时间和AUC值、几何均值(g-mean),其中:
(18)
(19)
TPR和FPR分别表示正类数据的分类精度和负类数据错分的比率.
3.1 人工数据集
本节中使用的人工数据集banana如图1所示,将其中一类作为正常数据,另一类作为异常数据,然后在异常数据中选取了10个样本点改变类别,成为噪音数据. 在无噪音、有噪音的情况下OCSVM、MKOCSVM、FMKOCSVM三种算法的分类表现分别如图2、图3所示,其中OCSVM的参数v=0.07,σ=2,MKOCSVM、FMKOCSVM的基础核均为7个高斯核,核参数均为{2-5,2-4,2-3,2-2,2-1,20,21}. 上述参数都是经过多次试验的最优参数.
从图2中可以看到,在没有噪音的情况下,三种算法的分类效果几乎没有差别. 有噪音时,如图3(a)、3(b)所示, OCSVM、MKOCSVM分类边界受到噪音影响,分类性能显著降低,但是图3(c)中FMKOCSVM的分类效果要优于OCSVM、MKOCSVM,与无噪音下的图2(c)无明显差异,几乎不受噪音影响,这表明在MKOCSVM中引入模糊隶属度后具有抗噪音能力,对提高算法的鲁棒性是有效的.
3.2 标准数据集
为了进一步评估所提出方法的有效性,在16个标准数据集上对比了FMKOCSVM与MKOCSVM、OCSVM算法的性能. 数据集的相关信息见表2. 其中数据集creditcard_cut来自kaggle上的信用卡欺诈检测数据集,由于原始数据集数量过于庞大,只随机选取729条交易信息(483条正常交易,249条欺诈交易). 其余15个数据集来自加州大学欧文分校提出的用于机器学习的数据库,每种数据集的类别为两类或者多类,为了适用于本文一类分类器的评估任务,对数据进行了重新组织. 对于每个数据集,将其中一个类别作为正类数据,其他类别的数据都作为负类数据. 在正类数据中随机选取70%的部分作为训练集,又随机选择负类数据的20%与训练集一起计算训练样本的模糊隶属度. 剩余的数据都作为测试集. 本次实验主要为了评估FMKOCSVM的抗噪能力,故所有实验都随机选取一定数量的负类样本改变其类标签作为噪音加入训练集中. 噪音比例为训练集的10%. 训练模型之前所有训练集都将属性值放缩到[0,1],测试集按训练集的标准进行相应的调整.
在OCSVM中,所有数据集使用的核函数均为高斯核函数[1-2]:
(20)
参数v和σ采用十折交叉验证的方式选取,其中v的取值范围为{0.01,0.04,0.07,0.10,0.13,0.16,0.19},σ的取值范围为{2-5,2-4,2-3,2-2,2-1,20,21,22,23}. 在MKOCSVM、FMKOCSVM中,参数v同样通过十折交叉验证选取,取值范围与OCSVM的相同. 所有数据集的组合核均由7个高斯核作为基础核加权求和构成,其中每个组合核的7个高斯核参数统一设置为{2-6,2-5,2-4,2-3,2-2,2-1,20}. 求核权重的优化问题时参数δ设置为100. 表3中列出了经过十折交叉验证后选取的OCSVM、MKOCSVM和FMKOCSVM的最优参数值.

表2 实验数据集信息Tab.2 Data information
为了减小训练集的随机选取对实验结果造成的偶然性,OCSVM与MKOCSVM、FMKOCSVM都做了20次实验,将这20次实验的平均值作为最终的结果. 其中训练时间包含十折交叉验证选参时间. 三种算法的AUC值、g-mean值、训练时间的比较结果分别见表4~表6.
从表4几何均值的对比结果上看,本文提出的FMKOCSVM的性能是最好的. 在13个数据集上,FMKOCSVM具有最高的几何均值. 尤其是数据集australia、glass、japan、vowel(1)、creditcard_cut上,FMKOCSVM的分类表现更好,比OCSVM的几何均值高10%~27%. 在数据集balancescaleleft、heart、waveform上,FMKOCSVM比OCSVM的几何均值高4%左右. 在australia、balancescaleleft、japan、vowel(1)、waveform、creditcard_cut、biomed、breast、park9个数据集上,FMKOCSVM与MKOCSVM具有相同的核函数核参数设置,但是FMKOCSVM比MKOCSVM的几何均值高6%~20%. 其余7个数据集上FMKOCSVM的几何均值都要高于MKOCSVM. 这表明本文提出的FMKOCSVM模型可以有效增强MKOCSVM的鲁棒性,并且可以同时解决OCSVM的核选择难题和噪音敏感问题.
从表5三种算法的AUC值结果比较来看,FMKOCSVM在12个数据集上具有最高的AUC值.australia、glass、heart、japan、vowel(1)、creditcard_cut6个数据集上,FMKOCSVM比OCSVM的AUC值高5%~17%. 在australia、balancescaleleft、heart、japan、vowel、waveform、creditcard_cut、biomed、breast、park10个数据集上,FMKOCSVM比MKOCSVM的AUC值高3%~15%. 该结果进一步验证了所提出的FMKOCSVM算法具有抗噪音能力.
由表6可知,在同一个运行设备的前提下,FMKOCSVM虽然增加了计算模糊隶属度的过程,但是其训练时间并没有明显比MKOCSVM增加,所增加的时间可以忽略不计. 但是交叉验证选参的

表4 几何均值对比Tab. 4 Comparison of g-mean

表5 AUC值对比Tab.5 Comparison of AUC value

表6 训练时间对比Tab.6 Comparison of training time
OCSVM算法的训练时间明显高于MKOCSVM与FMKOCSVM,尤其是在样本数目大且属性多的数据集上,时间增加更加明显. 这是因为OCSVM算法在用十折交叉验证方法选核参数时需要重复训练多次分类器,每训练一次OCSVM模型的时间的复杂度约是O(N3), 故其在交叉验证选核参数的过程中消耗了大量的时间且时间与训练样本的数量有关,而MKOCSVM与FMKOCSVM算法不需要选核参数,当样本规模越大时,两种算法的时间差异越大, MKOCSVM与FMKOCSVM会更节约时间. 图4是三种算法在所有数据集上的平均训练时间,可以更加直观发现FMKOCSVM在训练时间上的优势,FMKOCSVM的平均训练时间仅占OCSVM的3.7%.
综上所述,与MKOCSVM、OCSVM相比,虽然FMKOCSVM并没有在所有数据集上的都具有明显优势,但是仍在所有数据集上取得了较优的结果,并且FMKOCSVM中组合核的核参数是任意选取的,所有数据集设置相同,OCSVM的核参数却是在一组核参数中选取的最优的. 上述仿真实验进一步验证了,本文提出的FMKOCSVM模型不仅避免了的核选择的难题,并且具有较强的抗噪音能力,应用范围广泛.
4 结论
本文针对OCSVM核选择难题和对噪声数据敏感问题,提出了模糊多核一类支持向量机算法,该算法在同时解决这两方面的问题上取得良好的效果.
1)多核学习方法可以同时使用多种核函数,避免核选择的问题,且刻画数据特征的能力更强,极大地提高了训练效率. 对目标数据引入模糊隶属度可以有效确定不同样本的重要程度,从而减弱噪音数据或孤立点的影响,提升多核OCSVM的鲁棒性.
2)该算法在标准数据集上的实验仿真结果表现最优,进一步证实了噪音环境下模糊多核一类支持向量机算法的可行性和有效性.
3)与现有的算法相比,以多核代替单核,对样本引入模糊隶属度,使其在核参数选取上极大地节约了时间,且同时提高了鲁棒性.
