良好的运算能力从理解算理开始

黄素娟

【摘要】 数学运算能力是每个人必须具备的一项最基本数学能力。真正良好的运算能力不但可以准确计算已经学习的相关计算题，还可以举一反三，可以用更灵活更为简便的方法解决运算问题。良好的运算能力需要建立在明算理、懂算法、会运用上，融理入法才是提高学生运算能力，让学生运算能力持续发展的法宝。本文就如何培养学生良好运算能力方面进行探索与研究。

【关键词】运算;算理;算法

数学运算能力是每个人必须具备的一项最基本数学能力，在日常生活中运用最广的一种数学能力。数学运算能力的培养贯穿小学整个阶段的每一个过程，培养学生必备的运算能力是小学数学学习中一项最重要的任务。《数学课程标准（2011年版）》指出：运算能力主要是指能够根据法则和运算律正确地进行运算的能力。运算能力从内容上包含数的运算能力和符号运算能力。从过程上看，良好的运算能力应该包含三个方面：算理、懂算法、会运用。良好的运算能力除了可以帮助学生正确计算，更重要的是可以帮助学生寻求合理简洁的运算途径解决问题，提高学生学习力。

在日常的教学中，经常会碰到一些老师认为，计算能力只是一种技巧，教学没有什么道理可讲，学生只要明白计算方法，再经过反复练习就可以达到正确、熟练的要求。是的，对于一个单元、一个学期的计算能力的确可以通过反复操练达到正确、熟练，但是真正良好的运算能力不但可以准确计算已经学习的相关计算，更重要的是还可以举一反三地进行知识的迁移，可以根据算理，选择更灵活更为简便的方法解决运算问题。我们不能想象一个连基本的计算原理和方法都模糊不清的学生能够灵活、简便地进行计算，会具有较强的计算能力。在没有明白算理的情况下，为了提高学生的运算正确率，教师通常是加大训练力度，反复练习，甚至是题海战术。但是结果往往不尽人意。大量反复的练习极易引起学生的反感，不求甚解的盲目练习，更会直接影响学生的学习积极性。《数学课程标准（2011年版）》明确指出了第一学段关于运算能力的总体要求是：“应重视口算，加强估算，提倡算法多样化;应减少单纯的技能性训练，避免繁杂计算和程式化地叙述‘算理”;第二学段总体要求是：“应重视口算，加强估算，鼓励算法多样化;应使学生经历从实际问题中抽象出数量关系，并运用所学知识解决问题的过程;应避免繁杂的运算，避免将运算与应用割裂开来，避免对应用题进行机械的程式化训练。由此可见，无论是哪一个学段的要求，都需要减少单纯的技能训练、程式化训练。良好的运算能力应建立在明算理、懂算法、会运用上，融理入法才是提高学生运算能力，让学生运算能力持续发展的法宝。

一、整体把握教材，让计算教学有的放矢

北师大版教材关于运算的内容设计安排条理清晰，目标明确。纵观小学阶段关于运算的内容，可以分为三部分：整数运算、小数运算、分数运算。从符号的运算可分为加法运算、减法运算、乘法运算、除法运算。可以整理如下图：

从整数运算到小数运算再到分数运算，其实符号运算的意义都是相同的。如：加法都是求几个不同加数的和，乘法都是求几个相同加数的和的简便运算。但是在内容教材的安排循序渐进，环环相扣，螺旋上升。如果学生明白加法与乘法的意义，不管题目出现的是整数、小数、分数的运算，学生都可以从容、准确的列出相关算式，甚至可以根据符号运算的意义尝试计算。因此，教师一定要对教材运算内容的安排与要求心中有数，才能做到有的放矢。在进行教学时，要让学生从实际问题中抽象出数量关系，让学生真正理解符号运算的意义，再进行解释与运用。学生真正掌握运算符号的意义，不但可以解决目前遇到的问题，还可以利用知识迁移解决目前还没有学过的相关的问题，知其然更知其所以然，那又何须大量重复机械的训练！不懂算理，光靠机械训练，怎么可以适应千变万化的具体情况，怎么谈得上灵活运用？

二、鼓励算法多样化，让学生用自己的方式理解算理

在日常的教学中，经常会遇到一些老师对算法多样化不屑一顾，认为算法根本没有必要多样化，只需要好好掌握列竖式这种方法即可，理由是竖式计算简便、正确率高。其实，学生年龄越小，抽象思维能力越差。竖式是作为一种抽象的数学模型，很多学生，特别是学习水平较低的学生是难以理解的。教材安排算法多样化恰恰就是站在孩子的角度，用孩子的现有的知识经验对算理构建自己独特的理解。小学阶段的算法主要有用计数器拨一拨、利用小棒摆一摆、利用点子图圈一圈，利用表格分一分、算一算（整理如下图）……计数器可以生动的还原加减法竖式的意义，利用计数器来计算的过程就是竖式加减法的数学模型;点子图则可以生动体现了竖式乘法的算理，以及转化的数学思想：把一位数乘两位数转化成一位数乘一位数（或整十数），同时还渗透了乘法分配律的运算定律;利用表格可以具体地展现乘法竖式每一步的含义。教材在不同运算内容，分别运用了计数器、竖式、点子图、表格等运算工具，目的在于累积学生的活动经验，建立数学模型，让学生更好的理解算理。计数器、竖式、点子图、表格等是学生理解算理的桥梁与最有力的工具。如果教师不重视利用这些有力工具帮助学生掌握的算理、而直接引导学生用竖式计算结果，则很难达到对知识的真正理解。

三、善于比较分析，沟通多种算法之间的联系

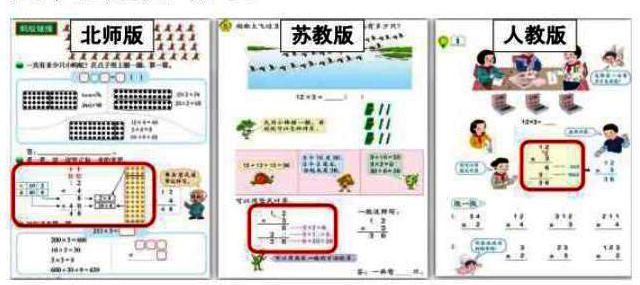
算理是运算正确的前提和依据。现行的三个版本的教材：北师大版、苏教版、人教版都非常注重算理的理解。下面是三个版本的教材分别就两位数乘一位数不进位乘法进行对比：

通过三个版本的教材对比，我们会发现，每个版本的教材都会特别重视让学生理解乘法竖式每一步表达的意义。但是，苏教版与人教版的教材是从抽象的竖式中理解算理。而北师大版教材对算理的理解力度更大，不但建立多种数学模型支撑算理，也通过了观察对比，分析各种算法中的联系，沟通各种算法之间的关系，进而实现对算法深入理解。在教学的过程中，我首先让学生用自己喜欢的方法计算12×4的结果，在让学生充分的交流展示，让学生明白每一种算法的计算方法，理解每一步的含义。如果教学就到这里结束，学生会产生很大的疑惑，为什么要学习这么多方法，这些方法之间有什么联系？如果没有得到合理的解释，学生对几种算法的理解是零碎的，不系统的。所以，我在教学中创设了这一环节：找朋友，让学生认真观察对比，把几种算法中的“朋友”连起来，说一说它们为什么可以成为朋友，利用这个生动的情境，让学生沟通表格、竖式、点子图几種算法之间的联系，大大加深学生对算理的理解，帮助学生形成知识网络。