抓住课题关键词 落实教学内容

摘 要： 本节课是苏科版八年级上册第一章第3节第6课时《1.3探索三角形全等条件（6）》。金老师紧紧抓住课题中的关键词“探索”，围绕“探索”前后进行了三次动手操作探索活动。三次活动由易到难，环环相扣，学生在不知不觉活动中掌握了知识。

关键词： 数学;三角形全等;教学

江都区乡村初中数学骨干教师培育站的学习于2019.9.6在乡村武坚中学继续进行。一共听了三节课，其中两节是有生上课，第三节是无生上课。老师们的精心准备，学生们的默契配合、积极参与动手操作活动给笔者留下深刻的印象，其中来自小纪中学金国平老师的“探索三角形全等条件6（sss）”这节课行云流水，水到渠成，实现了“做中学”的理念。正如荀子所说：“不闻不若闻之，闻之不若见之，见之不若知之，知之不若行之，学至于行之而止矣。”以下就分享金老师的教学过程。

一、 活动探究

（一）探索活动1，用一根长20cm的铁丝围一个边长为5cm、6cm、9cm的三角形

课前金老师做了充分的准备，为每位学生准备了一根长20cm的铁丝。此时所有的学生都动起手来，拿出了直尺先量出5cm然后弯折，再量出6cm、9cm后依次弯折最后学生们做成了一个三角形。

师：要求同桌的两个同学围成的三角形去重叠一下，观察有什么现象？

生1：重合。

师：在这个过程中有哪些元素相等的？

生2：三个角相等。

生3：不對！应该是三条边相等。

师：能不能给出猜想的结论？（初步感知）

生4：三条边相等的两个三角形全等。

没有华丽的情境导入，直接以问题驱动为课堂导入语，提出一个实际问题，激发起学生的动手操作欲望。在课堂上如果学生从头到尾都是观众，听老师娓娓道来势必会走神，长期静坐一定会显出困意。动手活动好比一块磁铁，金老师就是操纵磁铁的人，正引着学生一步一步地走向知识的殿堂。

活动一的教具是学生非常熟悉的铁丝，易弯折，易度量，是现实生活中的一个实际问题，数学课堂易操作。不过在操作的过程中会或多或少存在着误差，这只能是初步感知，为此金老师设置了第二个活动。

（二） 探索活动2，画△ABC，使BC=4cm，AB=2cm，AC=3cm

活动1是利用铁丝弯折成一个三角形，而活动2是画一个三角形，这是个抽象的过程，是个数学建模的过程，难度加大。这里金老师明显给学生“挖”了个坑，只说去画，却没说怎么画，更没说用什么工具去画。为了突破这个问题，金老师让一位学生上黑板尝试着画，其余学生在下面进行。这位学生首先利用有刻度的三角板画了一条长度为4cm的线段BC，也就是定下了三角形中的两个顶点B和C。学生在确定第三个顶点A时，尝试了好多次勉强把A点定下来。完成后金老师对所画的图形进行了度量验证，误差很大，不能准确定位A点。这是绝大多数学生的困惑之处，这是画图的重点，更是个难点。学生自身能解决的问题老师坚决不讲，学生有困难的问题老师要及时出场，但金老师不是直接告知学生如何如何去画，而是用了一个类比思考的方法去指明解决问题的方向而不是最终的结果。重在“探索”二字，留给学生足够的思考时间和空间，就像导师一样给你一个方向边走边想。

金老师提出了如何确定不等式组 x+2>3

x-1<4 的解集？需要满足几个条件？那么需要确定的A点需要几个条件？如何确定？这个类比引导太巧妙了！

师：确定A点需要几个条件？

生5：两个。

师：哪两个条件？

生6：AB=2cm，AC=3cm。

师：先画一个点A到B点的距离为2cm，能不能再画几个？

生7：学生用有刻度的三角板画了几个点。

师：如果全部画出来形成什么图形？

生8：一个圆。

师：那么A点需要满足的第二个条件是什么？

生9：以C为圆心，3cm为半径的圆。

师：那么A点在哪里？

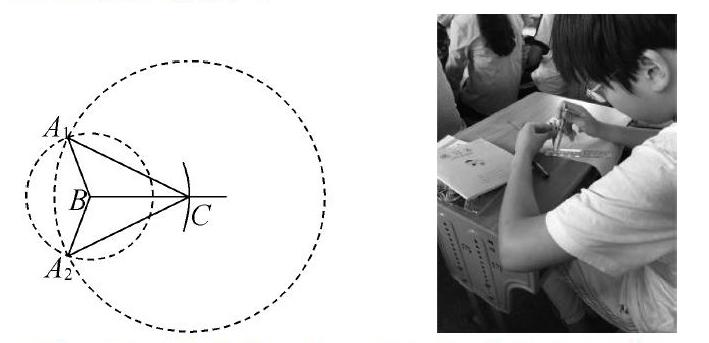
生10：既要在以C为圆心，3cm为半径的圆上，又要在以B为圆心，2cm为半径的圆，所以在两个圆的交点处。

师：很好，请你到黑板上画出A点。

生10：所画图形。

至此，学生能够顺利画出符合要求的图形。金老师让学生把其中一个三角形用剪刀剪下去和另一三角形重合，观察是否重合？经过活动2得到的三角形比活动1弯折得到的三角形更加精准，更能够让学生相信“三边相等的两个三角形全等（SSS）”这个“基本事实”。在根据三边长画三角形时，教师没有包办，直接演示讲解如何作图，而是让学生尝试多次而不得解时，追问如何能准确作出，从而引导学生积极思考，师生共同探索出交轨法，同时也渗透了尺规作图中规的作用。金老师的这节课，在教师追问方面，做得非常好。追问指向数学本质，“这些全等方法有什么共同点”，师生对话直击数学本质;追问把握时机恰当。

（三）探索活动3，感受三角形的稳定性

分别拉动三角形、四边形、五边形的两边，它们的形状、大小会发生变化吗？（事先准备的教具）同样是先动手操作感受，后给出三角形稳定性的性质，最后让学生列举该性质在生活中的运用。

1. 例题教学

已知：如图，在△ABC中，AB=AC.

求证：∠B=∠C

师：如何证明两个角相等？

生11：通过三角形全等的性质对应角相等去证明。

师：可是图中只有一个三角形啊？

生12：把它变成两个三角形。

师：怎样变成两个三角形？

生13：作辅助线。

师：你来试下？

生13：作了一条高，但是无法证明。（此时学生未学过HL，以后会学到，肯定学生的想法。）

师：谁来帮忙？

生14：作了一条顶角平分线，此时可以证明（SAS）。

师：还有不同想法吗？

生15：作底边上的中线，用今天学得SSS可以证明。

例题教学过程，金老师同样是耐心指导，放手交给学生讨论思考，教师只是适时地追问引导罢了。一切以学生为本，培养独立思考合作解决问题的能力，调动学生的学习热情，勇于发表各自的见解。

2. 课堂小结

本节课，你有哪些收获？提醒学生从知识、技能、经验、思想这几个方面去小结，不同的学生有不同的收获，对于敢于发言的学生及时给予肯定和鼓励。

生16：学到全等判定的新方法SSS。

师：还有什么方法？

生17：SAS、ASA、AAS。

师：这四种方法的共同特征？

生18：都是三个条件。

师：四种方法中三个条件（元素）都有什么共同元素？

生19：边。

师：还有吗？

生20：类比的数学思想，用不等式组的解类比出如何找出满足两个条件的点。

……

二、 总结

本节课，紧紧抓住“探索”二字，執教者一步一环把学生引向知识的深处，很好地完成了教学任务，是在学生不知不觉的动手操作过程中接受了证明三角形全等的又一个基本事实SSS。整个教学过程行云流水，水到渠成，执教者轻松驾驭，学生既学到了知识，又培养了动手操作的能力。数学教学中的动手操作是学生学习数学、感悟数学的一种重要方式。教师在实际的教学中，要注重操作的必要性和实效性，给予学生充分的操作时间，培养学生良好的操作习惯，让动手操作不流于形式，从而提升学生的数学素养。

参考文献：

[1]何小亚.数学核心素养指标之反思[J].中学数学研究（华南师范大学版），2016（13）.

[2]涂荣豹.中学数学教学案例研究[M].北京：北京师范大学出版社，2011.

作者简介：  焦鸥，江苏省扬州市，扬州市江都区宜陵镇中学。