基于供需关系的共享停车能力

张陈楠 董洁霜 孙 浩 刘魏巍 倪 敏

（上海理工大学管理学院 上海杨浦 200082）

0 引言

随着经济发展以及汽车保有量的增加，停车需求与日俱增，而城市停车基础设施建设相对完善，停车能力基本达到饱和状态，停车问题日益加剧。在共享经济快速发展的时代潮流之下，共享停车的理念应运而生。

共享停车在1984年的美国城市土地协会上首次提出。陈欣[1]指出：“共享停车的理念为利用不同用地性质间停车需求的时空互补性，实现停车需求从高峰场所向低峰场所转移。”由于停车位距离目的地的可接受距离通常为500m左右，所以该文章确定共享停车的服务半径为500m。

对于停车管理，Todd Litman[2]曾指出停车管理就是利用的各种政策和方案使停车资源得到更有效；陈欣[1]也提出借助动态差别定价调节供需关系。停车问题本质为供需在时间和空间的不均衡，该文章的研究中，将探索相应的管理策略使得停车供需在时间和空间上尽可能达到均衡状态，实现共享停车能力最大化。

1 共享停车供给曲线分析

1.1 时间-共享停车供给函数（T-N函数）

在构建可供给的共享停车泊位数与时间的函数关系式时，改变时间序列，将时间轴取第一天下午16：00至次日下午16：00。该函数图像大致呈上凸式抛物线状，两端低，中间高（改变时间序列后公共建筑共享停车供给示意图）。这符合供给时间越长的停车泊位，数量越少的常规，图1为共享停车供给曲线的演变过程。

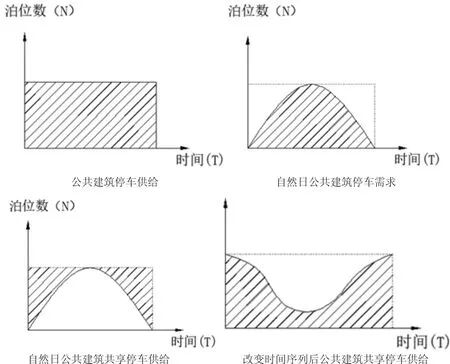
图1 时间-共享停车供给曲线变化

郭放[3]根据前人研究成果指出，预留泊位数量建议为配建泊位数量的5%~10%倍以应对突发事件。因此，将公共建筑物停车泊位对外共享时，将公共建筑物空闲停车泊位总量的90%作为共享停车供给总量，剩余10%的停车泊位来应对弹性需求。

1.2 共享停车供给函数几何意义解释

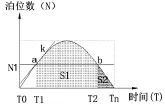
图2 共享停车供给函数

做一条平行于时间轴的平行线，与共享停车供给能力函数曲线相交于 a，b 两点，对应时间轴上 T1，T2。

（1）a、b 两点间的时间差记为△t1，△t1=T2-T1；对应 N 轴上的 N1：表示有N1个停车泊位数一定能提供时间长度为△t1的停车时间；

（2）△t2=Tn-T2，为可能供给停车时间，△t2由该停车泊位上的停放车辆和供给的停车时间共同决定。△t2是在泊位数减小后的时间，意味着可能泊位被占用，也可能该泊位未被占用，所以称△t2为可能供给停车时间。

（3）共享停车供给函数与对应T轴上△t1段之间所形成的图形面积S1，表示有N1个车位一定能提供时间长度为（b-a）的停车时间，因此称S1为每一个车位的绝对停车供给能力。

（4）对应△t2，则称S2为可能供给停车能力。

2 共享停车需求曲线分析

2.1 时间-共享停车需求函数（T-N函数）

居民区的主要停车需求主要在非工作时间，停车需求曲线在一天二十四小时时间段内呈现两端高、中间低的下凹型抛物线（自然日居民区停车需求示意图）。在改变时间序列之后，即将时间轴取第一天下午16：00至次日下午16：00，该函数图像大致呈上凸式抛物线状，两端低，中间高（改变时间序列后居民区停车需求示意图），图3为停车需求曲线的演变过程。

图3 时间-共享停车需求曲线变化

2.2 共享停车需求函数几何意义解释

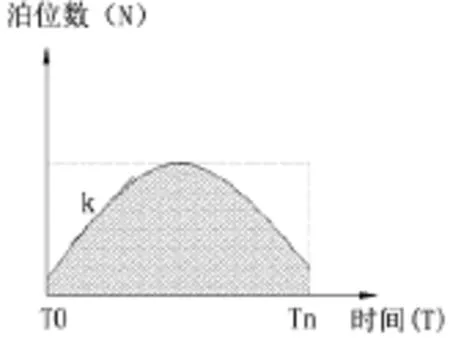
图4 共享停车需求函数

3 停车泊位共享能力研究

3.1 共享能力概念解析

共享能力，是由需求和供给两方面共同决定的。需要分析公共建筑物的共享停车供给能力和共享停车供给和居民区共享停车需求的关系。在时间-停车泊位数的坐标系中构建共享停车需求与共享停车供给的函数图像，记共享停车供给函数为P（t），共享停车需求函数为D（t），则共享停车能力 C=[∫P（t）dt]∩[∫D（t）dt]。

3.2 共享停车供给——共享停车需求分析

由于共享停车泊位数量和需求供给相关，难以确定；因而本文从共享时间上去考虑，共享停车供给和共享停车需求会存在以下两种情况：

图中参数解释：

S1：共享停车需求曲线和共享停车供给曲线的重合部分，为共享停车能力；即 C=[∫P（t）dt]∩[∫D（t）dt]=S1。

S2：共享停车供给曲线未能覆盖共享停车需求曲线的部分，为潜在共享能力。

S3：共享停车供给曲线超过共享停车需求曲线的部分，为闲置共享能力。

△N=max{D（t）-P（t）}：表示共享停车需求与共享停车供给在数量上的最大矛盾。

△t=|Tp1-TD1|：表示共享停车需求与共享停车供给在时间上的最大矛盾。

（1）P（t）∩D（t）≠ø：

共享停车供给曲线和共享停车需求曲线在时间和空间上有交集，可以实现停车泊位共享，停车泊位存在共享能力。

图5共享停车能力情况一

图5 中表示共享停车需求曲线和共享停车需求曲线在时间和空间上有一部分重合，可以在一段时间内实现停车泊位共享。但共享能力未达到最大值，会出现阶段性停车资源浪费和停车资源紧张的现象。

图6共享停车能力情况二

图6 左图表示共享停车供给在时间和空间上都不能完全满足共享停车需求，此时停车泊位的共享能力就等于共享停车供给能力∫P（t）dt，已经实现了共享停车能力最大化。图6右图表示共享停车供给能够在时间和空间上完全满足共享停车需求，同时还出现了停车资源浪费的现象，此时的停车泊位共享能力就等于∫D（t）dt，可通过增加共享停车需求来使得共享停车能力最大化。

（2）P（t）∩D（t）=ø

此部分介绍的是共享停车需求和共享停车供给在时间和空间上没有交集，如图7所示。即此种情况下不能实现停车泊位共享，共享停车车能力为0。

图7 共享停车能力无法实现的情况

4 结语

本文研究公共建筑配建停车泊位对居民区的共享停车能力，分析了共享停车供给曲线和需求曲线的关系，提出与图像相对应的管理措施。

本文研究的停车泊位共享能力建立于共享停车供给和需求曲线均类似于抛物线的假设上，且是针对大城市而言：在中午不会出现大量机动车驶离公共建筑物且周边居民区在中午不存在大量的停车需求。且文章只对共享停车能力进行了定性分析，并没有定量化，后期还学借助其他模型，进行定量分析。