双向驱动的柔顺结构微动平台的设计与测试

罗展鹏，李国平，韩同鹏，杨依领，赖文锋

(宁波大学 机械工程与力学学院，浙江 宁波 315211)

0 引言

微位移技术作为精密机械和精密仪器的关键技术之一已得到迅速发展，微动平台作为传递位移与力的微位移机构也得到了广泛应用。在精密与超精密机械加工中，微动平台可实现微进给或加工误差的精密补偿；在精密测试中，微动平台可作为承载机构实现精密仪器的微调节或微定位；在微探针扫描成像中，配合微探针、微夹钳使用，可对微结构表面进行精密测量等[1-2]。在微动平台技术中，压电陶瓷致动器由于具有刚度大，响应速度快，分辨率高等优点，被广泛用作驱动元件[3-4]。

鉴于压电驱动微动平台的应用较广，国内外很多学者都进行了广泛的研究。如朱吴乐等[5]将叶型双平行四边形结构与Scott-Russell和半桥机构组成的柔顺放大机构相结合，研制出用于纳米定位的平行两自由度压电驱动的柔顺微动平台，测试结果表明，微动平台的放大倍数为5.2，一、二阶共振频率分别为570 Hz和585 Hz。田延岭等[6]采用对称平行四连杆机构与柔性杠杆放大机构相结合，研制出二维微纳米定位平台，其最大位移为50 μm，x、y方向的固有频率分别为143 Hz和180 Hz。李阳明等[7]采用桥式放大机构和复合平行四边形机构设计了xy完全解耦微动平台，该平台位移放大率为5.85，平台工作范围约为117 μm×117 μm。同时,唐辉等[8]采用双平行四边形结构和柔性杠杆放大机构相结合，研制出压电驱动的二自由度微动平台，实验测试显示，微动平台的放大率为4.2，x、y方向的最大位移分别为119.7 μm×121.4 μm。秦燕定等利用杠杆机构放大位移，叶型平行四边形机构进行解耦，研制了二自由度微动平台，实验结果显示平台具有超过82 μm×82 μm的工作空间，一阶固有频率为423 Hz[9]。Choi等[10]基于菱形机构放大原理研制出二自由度微动平台，实验测得微动平台最大位移可达124 μm，x、y方向固有频率分别为350 Hz和377 Hz。Elfizy等[11]采用四连杆机构，设计二自由度串联结构微动平台，测试可知其最大位移可达80 μm，一、二阶固有频率分别为650 Hz和680 Hz 。

上述这些柔性结构微动平台能实现一定程度的位移放大，在精密机械和精密仪器运用领域有广泛的应用。但这些常见平台都是压电陶瓷单向驱动，而国内对压电陶瓷双向驱动的微动平台研究较少。李国平等[12-13]设计了一种对称布置两个压电陶瓷致动器，利用杠杆机构进行位移放大的伺服刀架，刀架的位移放大比为1.65，一节固有频率为871.86 Hz。刘雪瑞等[14-15]基于三角放大原理，改进设计了以柔性铰链为传动结构的菱形微位移放大机构，实现了机构的双向主动驱动，放大倍数为2.4，同时在此基础上设计了二维压电微动平台，平台在x、y方向上行程分别为41.6 μm和42.9 μm。

本文设计了一种基于压电双向驱动的二维微动平台。两组压电陶瓷驱动器分别对称放置在平台输入端，给平台的进给和回复提供驱动力。利用Scott-Russell机构和杠杆机构实现位移两级放大，平行四边形机构实现平台输出解耦。该文重点分析计算了平台的放大率、刚度、一阶固有频率等静动态特性，通过ANSYS软件对平台进行了仿真分析，并搭建实验测试系统,且对平台的静、动态特性进行测试。

1 微动平台结构设计

为了提高微动平台的响应速度和放大倍数，本文设计的基于双压电对称驱动的微动平台，其总体结构如图1所示。图中，PSA1～4为压电致动器。

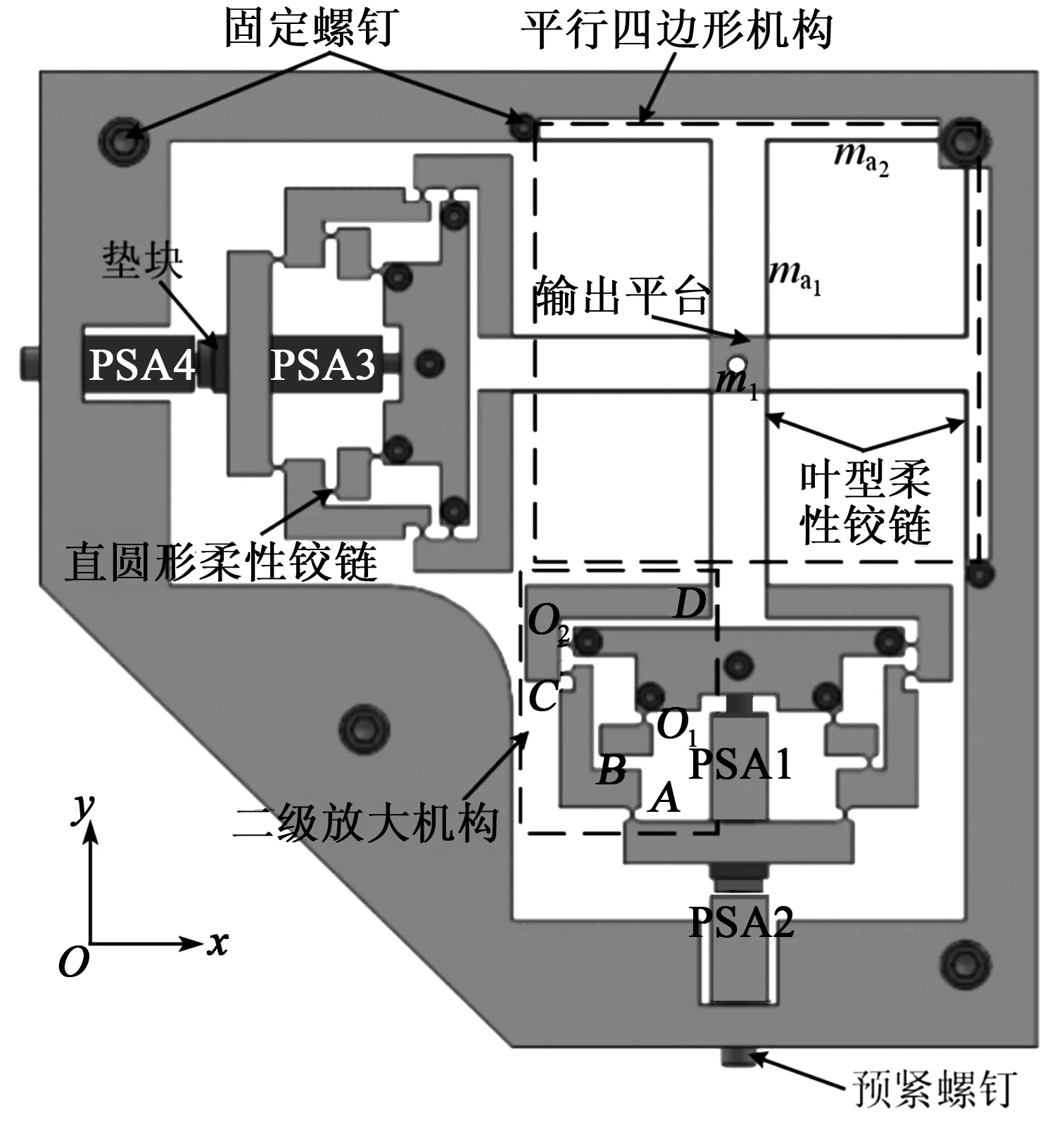
图1 微动平台结构设计

由图1可知，该微动平台由两组直圆柔性铰链制成的二级放大机构、叶型柔性铰链制成的平行四边形机构、输出平台、压电致动器(PZT 150/7/10 VS12)及其输出调整机构组成。压电致动器输出调整机构由垫块、预紧螺钉和固定螺钉构成。平台在x、y方向均设有两组二级放大机构，使平台在x、y方向上均能独立输入。通过二级放大机构对压电致动器的输出位移进行放大，可实现微动平台的较大位移输出。同时，平行四边形机构保证微动平台平动输出，消除x、y方向运动时的位移耦合。

微动平台y方向的运动原理如下：Scott-Russell机构将PSA1沿y方向的输入位移(A处)正交传递到沿x方向(C处)，同时实现一级放大；再通过杠杆CO2D结构将位移传递到D处，实现位移的二级放大；最后，通过平行四边形机构连接输出平台，确保输出平台平动输出和位移解耦。同理，输出平台回复则由PSA2提供回复力。

x、y方向的运动原理相同,PSA3的输出位移经过Scott-Russell机构放大后传递到杠杆机构，实现位移的二级放大；最后，通过平行四边形机构连接输出平台，确保输出平台平动输出和位移解耦。同理，输出平台回复则由PSA4提供回复力。

按照二自由度、双向驱动、较大输出位移的设计目标，通过多次优化设计，确定了微动平台内各直圆型柔性铰链半径、叶型柔性铰链的厚度和长度，以及各连杆的长度和倾斜角度等结构参数。表1为各参数的尺寸。图2为y方向运动示意图。表1中，l1～l4、α、β和γ分别为图2中对应各连杆的长度和倾斜角度，la1、la2和t1、t2分别为图2中叶型铰链a1、a2的长度和厚度，rA～rC、rO1、rO2和tA～tC、tO1、tO2分别为对应各直圆型铰链的半径和厚度。图2中，Fi、ui分别为微动平台的输入力和输入位移，Fo、uo分别为微动平台的输出力和输出位移。

表1 微动平台结构尺寸

图2 y方向运动示意图

2 微动平台性能的理论分析

2.1 微动平台的运动输出分析

考虑微动平台结构在每个运动方向上均为对称结构，这里仅取放大机构的半侧进行分析(见图2)。

柔顺放大机构中连接关节A～D处的瞬时速度vA～vD为

vi=vA=ω3lO3A

(1)

vB=ω1l2

(2)

vC=ω3lO3C=w2l3

(3)

vD=ω2l4

(4)

vo=vDcosβ

(5)

(6)

式中：vi，vo分别为微动平台的输入和输出速度；ω1,ω2分别为构件O1B和CO2D的角速度；ω3为构件ABC的角速度。

联立式(1)～(6)，微动平台的位移放大倍数为

(7)

由式(7)可看出，λ与参数l3、l4、α和β有关。

根据刚体的运动学及由图2可知，给定输入角δi，转动关节O1、O2和A～D的偏转角可推导为

(8)

(9)

δA=δi

(10)

(11)

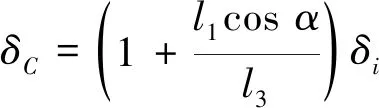
(12)

(13)

对于叶型柔性铰链a1和a2，其偏转角增量δa1和δa2可表示为

(14)

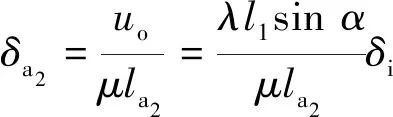
(15)

式中μ=0.85为特征半径系数。

2.2 微动平台的固有频率分析

忽略重力影响，微动平台的势能为

(16)

式中：KO1，KO2，Kj分别为直圆型铰链O1、O2和A～D的转动刚度；n=1，2表示叶型柔性铰链a1和a2；Kn为叶型柔性铰链a1和a2转动刚度，且

(17)

(18)

式中：E为弹性模量；rj，tj，b分别为铰链的半径、厚度和宽度；I为叶型柔性铰链横截面的惯性矩；ln为叶型柔性铰链的长度；Kθ为叶型柔性铰链的刚度耦合系数，通常取2.65。

微动平台的动能为

(19)

κA=1

(20)

(21)

(22)

(23)

(24)

(25)

(26)

拉格朗日方程用于平台的动力学建模，则有

(27)

式中ui，Fi分别为平台的广义输入位移和广义力。

将动能势能代入式(27)，平台的动态特性可表示为

(28)

式中M，K和F分别为微动平台的等效质量、等效刚度和广义力矩，且

(29)

(30)

(31)

所以，可获得微动平台的固有频率为

(32)

3 微动平台的有限元分析验证

为了验证已建立的微动平台的分析模型是否正确，通过ANSYS软件对微动平台模型进行有限元分析。所选材料为铝合金，设材料的弹性模量为71.7 GPa，密度为2 810 kg/m3，泊松比为0.33，屈服强度为503 MPa。

微动平台有限元分析的内容主要包括平台的放大倍数、固有频率和最大应力。为了分析平台放大部分的放大率，对机构输入端施加一定的位移载荷，得到平台最大输出位移和最大应力；为了分析刀具的固有频率，对平台进行模态分析，测得平台一阶固有频率。

首先，验证微动平台的放大倍数。在微动平台y方向的输入端处，沿y轴负向施加10 μm的位移载荷，分析结果如图3所示。由图3(a)可知，微动平台的放大结构部分最大输出位移为105.16 μm。由图3(b)可知，输出平台的最大位移为91.3 μm。相对于放大机构部分略有降低，这是由平台输出端平行四边形结构的阻抗效应引起的。因此，微动平台的放大倍数为9.13。

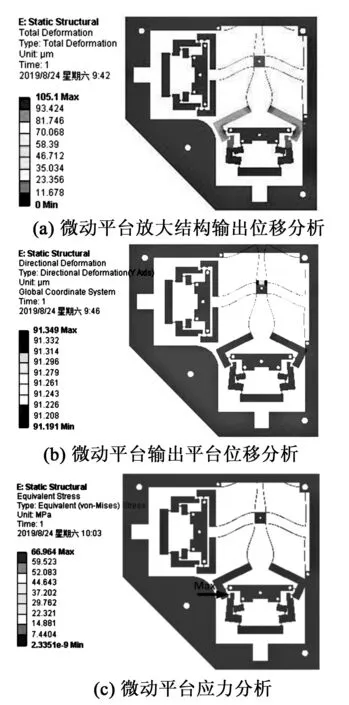
图3 微动平台放大倍数分析

同时，验证了输入载荷为10 μm时，输出平台在耦合方向的输出位移，其结果如图4所示。在y方向为主运动方向时，平台在x方向的最大耦合位移为0.11 μm，输出耦合比为0.12%，说明平台实现了很好的运动解耦。此外，微动平台在输出时，最大应力(66.96 MPa)发生在C处，远小于材料的屈服极限，如图3(c)所示。

图4 微动平台的耦合位移

其次，利用模态分析得到微动平台的固有频率，其结果如图5所示。由图可得微动平台的一阶固有频率为241.54 Hz。

图5 微动平台模态分析

同时，在y方向的输入端处沿y轴正向，以及在x方向的输入端处沿x轴正(负)方向，均施加10 μm的位移载荷，对平台位移放大率、最大应力及固有频率进行仿真分析，分析结果具有较高的一致性，说明微动平台在两个方向上正、反驱动均具有类似的动态特性。

表2为微动平台的放大倍数、固有频率的理论值和有限元仿真数值。由表可看出，理论分析值和有限元仿真值基本吻合，说明结构的理论简化较合理。

表2 微动平台的放大倍数和频率

4 平台输出特性的实验测试

为进一步验证理论计算和有限元分析的准确性，对微动平台进行实验研究。微动平台选用7075铝合金材料，通过线切割加工完成。

图6 为搭建的实验测试系统。该系统包括多功能卡、驱动电源、压电致动器、平台、激光传感器。测试过程如下：多功能卡上的模拟量输出板卡NI-9263接收来自计算机输出的控制信号，控制驱动电源(HPV-3C0150A0300D)将电压施加至压电执行器。压电致动器驱动平台输出位移，通过激光传感器测得。然后输出给多功能卡上的模拟量输出板卡NI-9239传入计算机内。

图6 实验测试系统

压电执行器型号为PZT150/7/5 VS12,最大输出位移为10 μm，标称刚度为90 N/μm。测微仪型号分别为LK-G10 和 LK-G30，检测分辨率分别为20 nm和50 nm, 量程分别为±5 mm 和±1 mm。

分别对PSA3和PSA4施加0.1 Hz、0～150 V～0 V的三角波电压信号，测得微动平台在x轴沿正、负两个方向驱动时的位移特性曲线如图7、8所示。

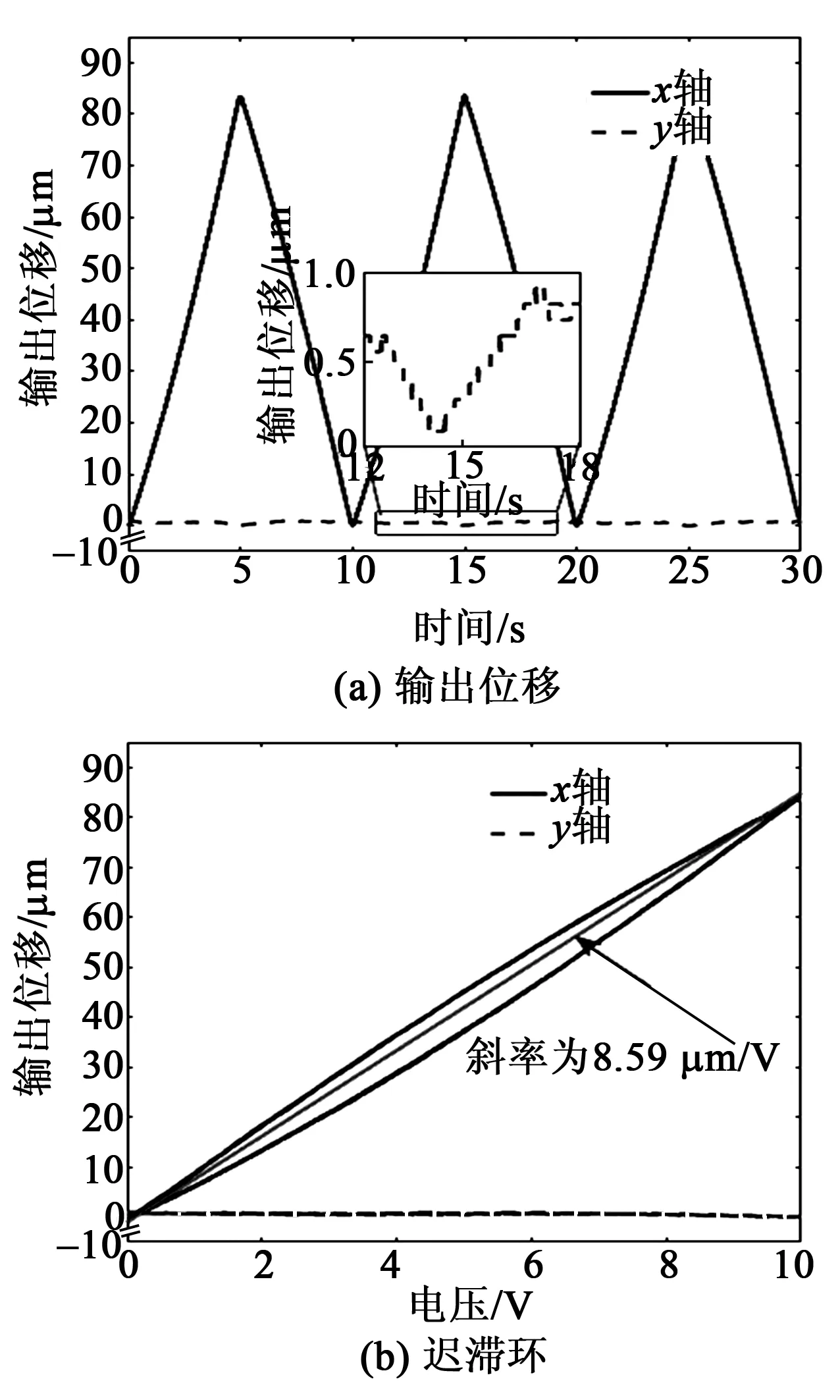
图7 x轴正向输出位移测试结果

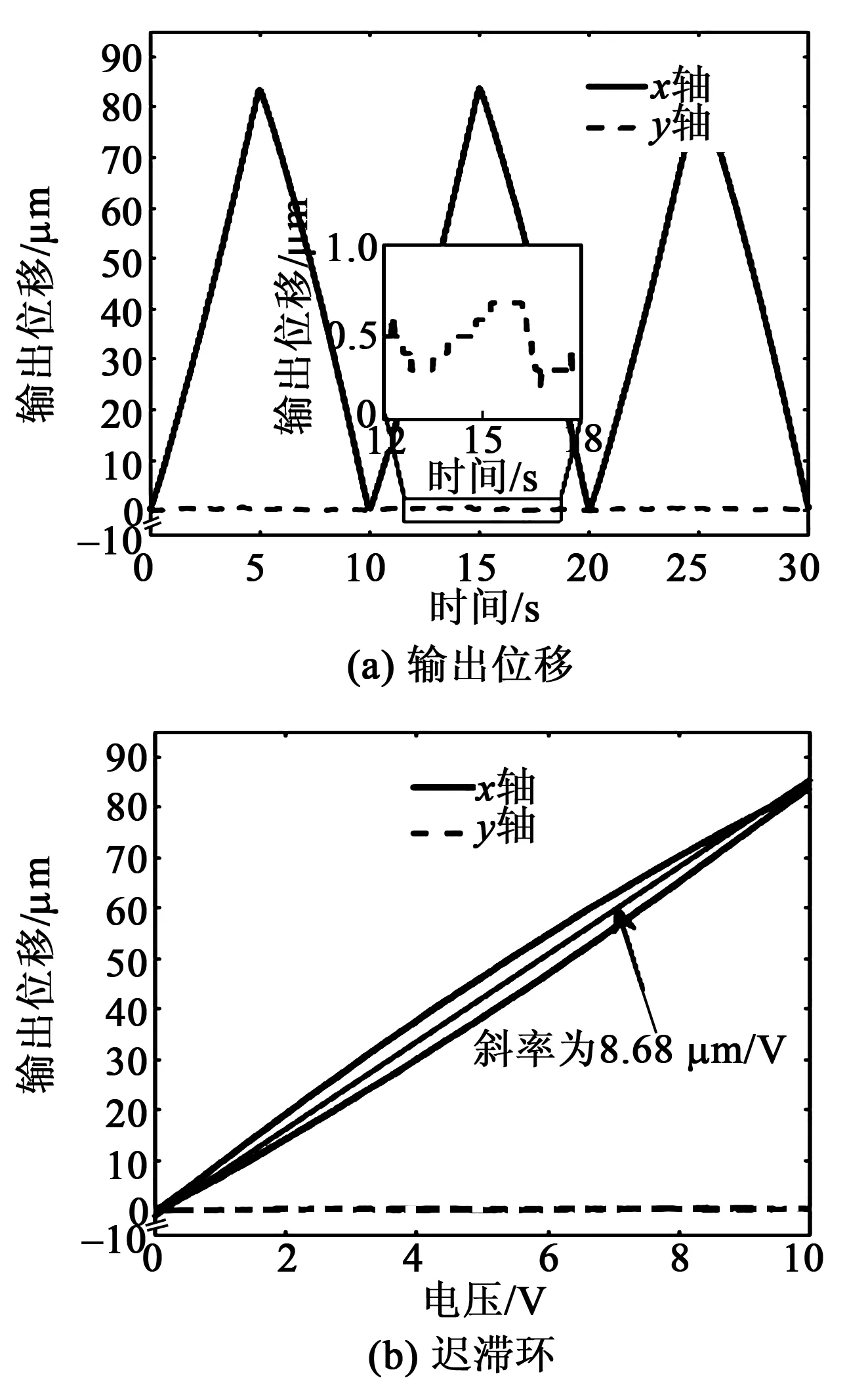
图8 x轴负向输出位移测试结果

由图7、8可知，x正、负向输出时，微动平台的最大输出位移分别为84.6 μm和-84.2 μm。在此电压信号下压电致动器的最大输出位移为10 μm，所以微动平台沿x轴正、负向输出的放大倍数可计算为8.46倍和8.42倍。此外，图7、8也给出了微动平台运动时的耦合位移曲线。当平台沿着主运动方向运动时，耦合方向的输出位移分别为0.70 μm和0.56 μm，输出耦合比为0.82%和0.67%。

同时，由于压电陶瓷的迟滞特性，也给微动平台带来了明显的位移迟滞现象(见图7、8)。经过拟合可知，平台沿x轴正、负向的迟滞环斜率分别为8.59 μm/V和8.68 μm/V， 两者误差较小，说明平台在x正、负向的运动性能基本相似。

分别对PSA1和PSA2施加相同的三角波电压信号，测得微动平台在y轴正、负向驱动时的位移特性曲线如图9、10所示。

图9 y轴正向输出位移测试结果

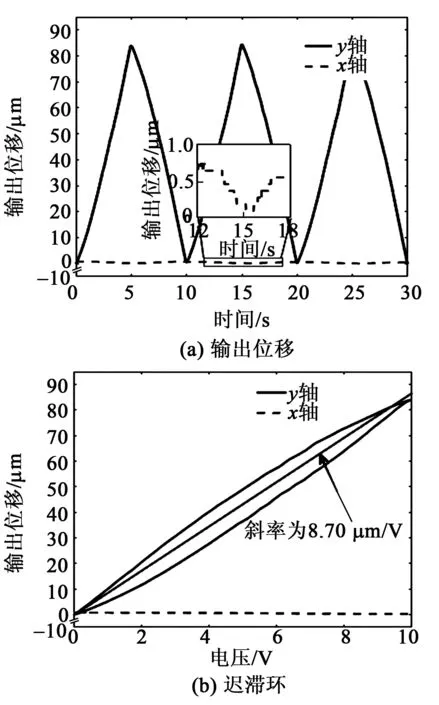
图10 y轴负向输出位移测试结果

由图9、10可知，y轴正、负向输出时，微动平台的最大输出位移分别为85.0 μm和-84.5 μm。所以微动平台沿y轴正、负向输出的放大倍数可计算为8.50倍和8.45倍。当平台沿着主运动方向运动时，耦合方向的输出位移分别为0.68 μm和0.59 μm，输出耦合比分别为0.80%和0.70%。同时，由于压电陶瓷的特性，给微动平台带来了明显的位移迟滞现象，经过拟合得到平台沿y轴正、负向的迟滞环斜率分别为8.56 μm/V和8.70 μm/V，两者误差较小，说明平台在y轴正、负向的运动性能基本相似。

幅值150 V的三角波信号，改变其信号频率，在0.1 Hz、0.2 Hz和0.5 Hz下，测得平台在x、y轴正、负双向输出幅值，每个频率下均取5组数据(见表3)，验证平台双向驱动时输出位移的稳定性。由表可知，实验条件相同时，不同频率正弦信号激励下，平台的输出幅值波动微小，在每个轴的正、负向输出具有较高的相似性和稳定性。

表3 部分实验数据及标准差

5 结束语

设计了一种基于两级放大机构的xy两自由度双向驱动微动平台。分析了微动平台的运动及放大原理，建立了微动平台性能的理论模型和有限元模型。平台输出特性测试结果表明，微动平台的放大倍数可达8.50倍，与仿真值误差为6.9%，同时耦合位移控制在0.82%以内；平台在150 V三角波信号驱动下，x轴上正、负向输出位移分别为84.6 μm和-84.2 μm；y轴正、负向输出位移分别为85.0 μm和-84.5 μm，不同频率下的最大位移只在极小范围内波动，在x、y轴的正、负向输出具有很高的相似性和稳定性。该平台实现了双向驱动，大行程、高精度的目的，说明理论建模和有限元分析的准确性，为双向驱动的微动平台研究提供了一定的理论基础。