Savonius型桨叶水动力特性研究

吴映江，宋瑞银，郑 堤，吴烨卿，陈炫光

(1. 宁波大学 机械学院，浙江 宁波 315211; 2. 浙江大学 宁波理工学院，浙江 宁波 315100; 3. 浙江大学 宁波研究院，浙江 宁波 315100)

近年来，传统化石能源储量有限及其使用所造成的环境污染问题日益突出，开发和利用可再生能源迫在眉睫[1]。海洋波浪蕴藏着巨大的能量，其分布广泛、容量巨大，与太阳能、风能相比，波浪能密度更大，持续时间更久，具有广阔的开发前景[2]，合理设计和使用桨叶可以有效地捕获波浪能。根据转轴相对于波浪方向的不同可将桨叶分为水平轴桨叶和垂直轴桨叶两种类型[3]。研究表明，垂直轴桨叶结构简单，能量捕获不受波浪方向影响，自启性能良好，具有广阔的应用前景[4]。

Savonius型(S型)桨叶是一种典型的垂直轴阻力型桨叶，国内外很多学者对这种桨叶开展了研究。Golecha等[5]研究了偏导板在S型桨叶上安放位置对功率系数的影响；Lee等[6]研究了S型桨叶在不同螺旋角和形状特征下的扭矩系数；Tutar等[7]研究了不同波高、周期下的3叶片桨叶的功率和转矩性能；Roy等[8]讨论了雷诺系数对S型桨叶动静态特性的影响；边佩翔等[9]研究了S型桨叶在不同叶尖速比与重叠比下的水动力及能量提取性能；李良乾[10]将斜度和拱度引入桨叶叶型，并对加装导流罩下的S型桨叶性能优化进行了研究；谢敏捷[11]研究了波流耦合作用下的桨叶动转矩特性和功率特性。陈俊华等[12]进行了在低流速下水平轴潮流能发电装置的桨叶研究。林躜等[13]研究了液压型潮流能发电系统中叶轮的功率控制。

目前，采用三维数值仿真方法对S型桨叶功率系数的研究相对较少。下文应用Fluent软件，基于UDF二次开发建立S型桨叶三维数值模型，通过数值仿真和模型试验研究S型桨叶重叠率、相对入水深度和开口率等参数对其动转矩系数和功率系数等水动力特性的影响。

1 S型桨叶工作原理及主要参数

S型桨叶主要由凹叶片和凸叶片组成，如图1所示。取柱坐标系orθz，使得orθ在静水面上，oz轴通过柱中心，向上为正，如图2所示。

图1 S型桨叶结构简图Fig. 1 Schematic diagram of S-type rotor

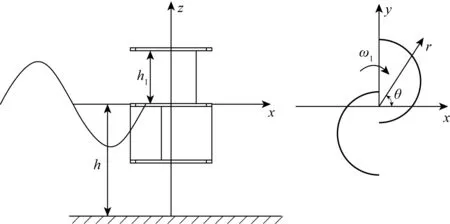
图2 桨叶在波浪中柱坐标系Fig. 2 Coordinate system of rotor in the wave

在极坐标系下，波浪对在水深h中，半径为d的S型桨叶入射势φi可写为[14]

(1)

式中：g为水平加速度，A为波幅，k为波数，ω为波浪频率，h为水深。S型桨叶上的水平波浪力可通过物面上的压强积分而得到，在线性理论下桨叶上的水平波浪力为

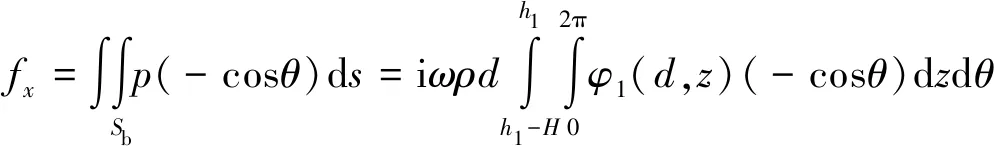
(2)

受力分为波浪越过桨叶和未越过桨叶两种情况，则一阶近似下的波浪作用力可写为

(3)

式中：ρ为流体密度，h1为桨叶在水面上高度，nx为物面单位法向量，nx=-cosq。取桨叶半径与水深之比为d/h=0.1，当h1≤A时，由式(3)可得桨叶上的水平波浪力如图3所示，波浪水平力随波数的增大而增大，并随着入水深度增大而减小。

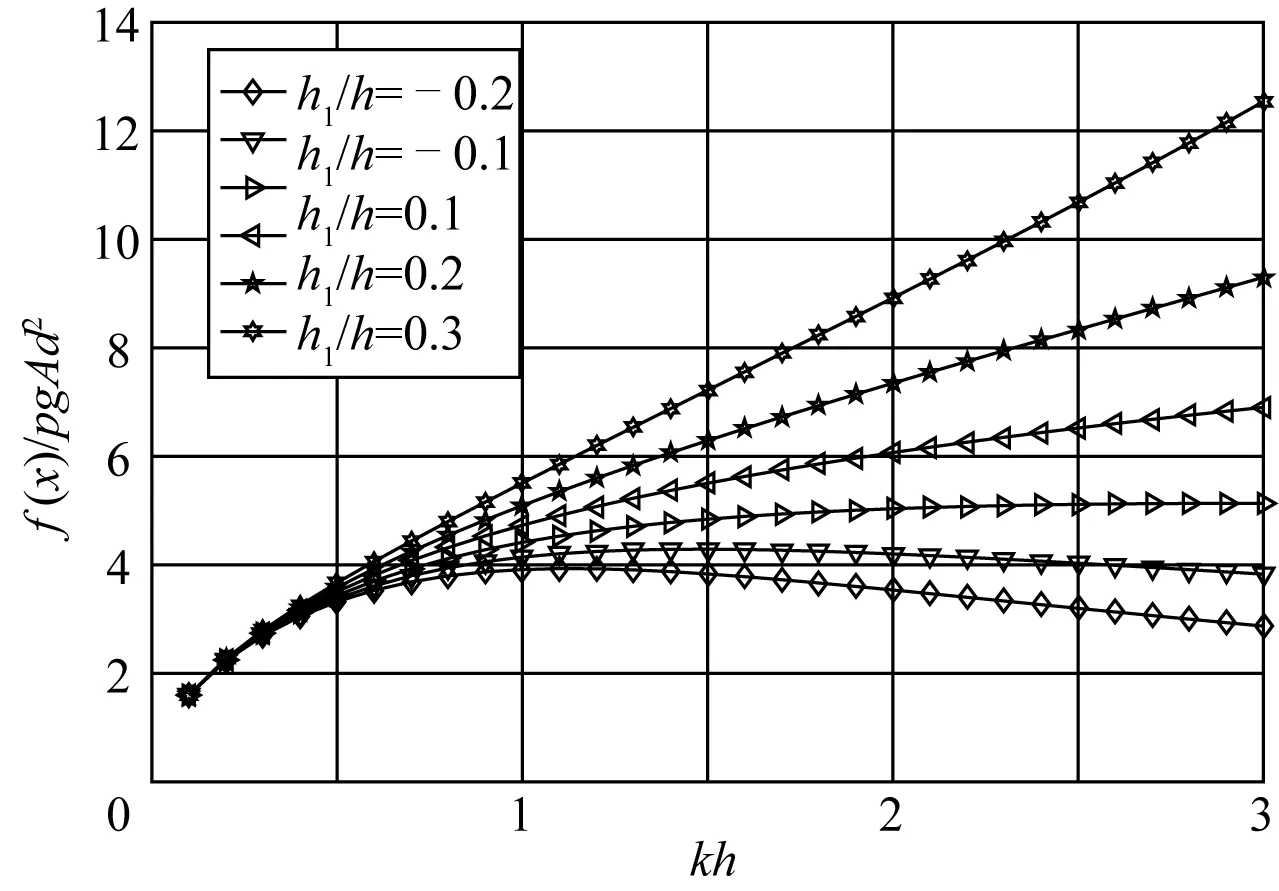
图3 桨叶上的水平波浪力Fig. 3 Horizontal wave force on the rotor

图4 S型桨叶的工作原理Fig. 4 Working principle of S-type rotor

在波浪冲击作用下，凹叶片上产生的驱动力矩大于凸叶片上产生的阻力矩，其转矩差可驱动桨叶旋转,工作原理如图4所示。凹叶片产生的驱动力Fd1和凸叶片产生的阻力Fd2可分别由式(4)和(5)确定，转矩差M由式(6)确定[13]：

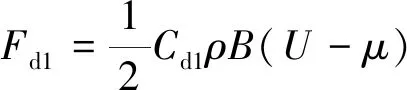
(4)

(5)

M=(Fd1-Fd2)(d-0.5s)

(6)

式中：Cd为阻力系数；U为来流速度；m为叶片平均速度；H为桨叶高度；B为桨叶相对于来流的截面面积，B=(2d-s)H；s为桨叶重叠部分的宽度，如图1所示。

影响S型桨叶性能的结构参数主要有重叠率、高径比、开口率和相对入水深度，其中重叠率e可按式(7)计算：

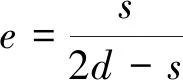
(7)

高径比按式(8)计算

(8)

由式(5)可知，减小凸叶片相对来流的横截面积可以减小Fd2，从而增大S型桨叶的转矩差。本文设计在桨叶叶片上增添单向开口的弹片阀，凹叶片上受水流冲击时，弹片阀处于闭合状态；凸叶片上受水流冲击时，弹片阀处于开口状态。开口率可按下式计算：

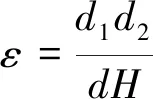
(9)

式中：e为桨叶的开口率，d1为弹性阀开口宽度，d2为弹片阀开口高度。相对入水深度λ可按下式计算：

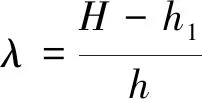
(10)

在分析桨叶性能时，需要用叶尖速比来衡量桨叶转动速度相对于流速的快慢。叶尖速比可按下式计算：

(11)

式中：TSR为叶尖速比，ω1为桨叶转动的角速度。

动转矩系数Cm和功率系数Cp是评估桨叶性能的重要参数，其计算公式分别为：

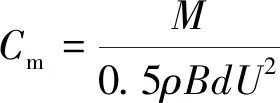
(12)

(13)

2 桨叶结构参数优化

在实际应用中，能量转换必然有能量损失。因此，在表达式(13)中引入传动装置的效率h1和发电装置的效率h2对桨叶功率系数Cp进行修正，得：

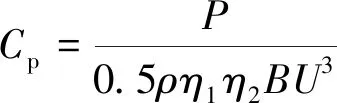
(14)

S型桨叶功率系数越大，单位时间内转换能量越多。在给定波浪流速U的条件下，S型桨叶结构参数是影响功率系数的重要因素。以叶片直径d、重叠宽度s和桨叶高度H三个主要结构参数为设计变量，以波能利用率最大为追求目标，建立桨叶结构优化模型如式(15)所示。取象山海域平均波速U=1.5 m/s，为保证年发电量，取P为300 W，目标函数Cp中r、h1、h2分别为1×103kg/m2、0.9、0.9。

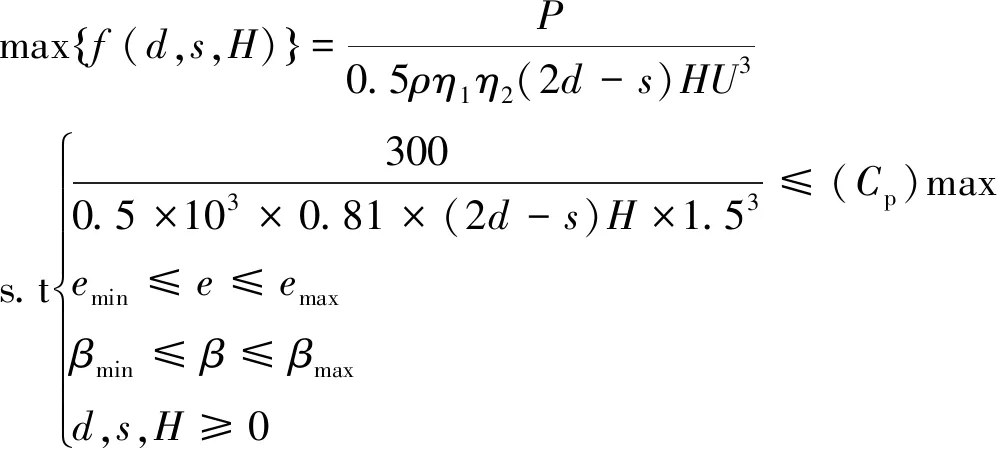
(15)

式中：Goh等[15]试验研究表明S型桨叶的功率系数(Cp)max为0.34；陈伟等[16]研究发现S型桨叶重叠率e为0 ～ 0.15和高径比b为1 ～ 1.5时性能最优。利用Matlab优化工具箱中fmincon函数求解该模型，其优化结果是，当主要结构参数取表1所列数值时，S型桨叶功率系数Cp达到最大值0.32。

表1 S型桨叶主要参数Tab. 1 Main structural parameters of S-type rotor

3 数值模拟与验证

3.1 数值波浪水槽

基于RNG k-ε湍流模型和VOF自由面捕捉方法，通过 Fluent 软件建立造波和消波功能的三维数值波浪水槽，如图5所示。利用 Fluent 用户自定义函数(UDF)定义边界水质点速度生成入射波；同时，针对数值波浪水槽末端区域，通过在动量方程中添加人工阻尼源项的方法实现动量源项消波[17]。

基于k-ε湍流模型，通过定义边界处水质点的速度进行造波。动量方程可表示为：

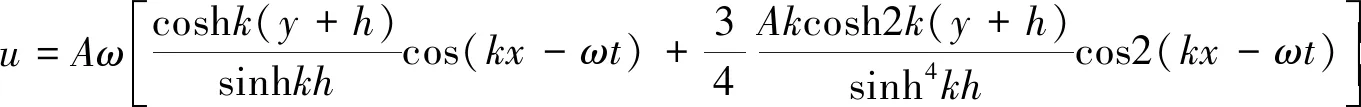
(16)

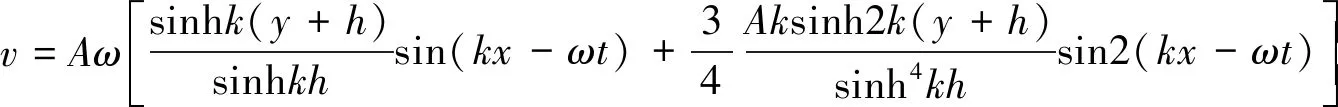
(17)

式中：u为垂直分速度，v为水平分速度，A为振幅，k为波数，ω为圆频率，h为水深。

在消波区的动量方程中加入阻力源项来消除反射波，动量方程可写为：

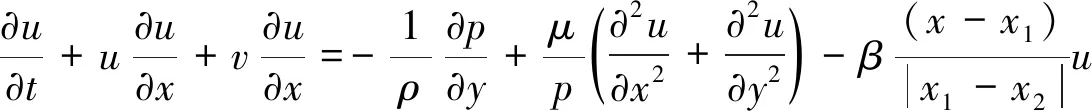
(18)

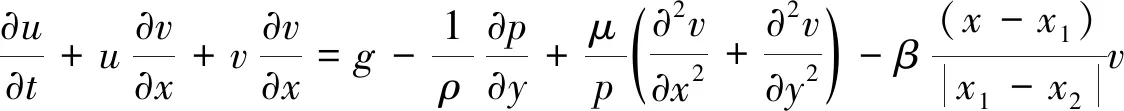
(19)

图5 数值水槽模型示意Fig. 5 Schematic diagram of the numerical sink model

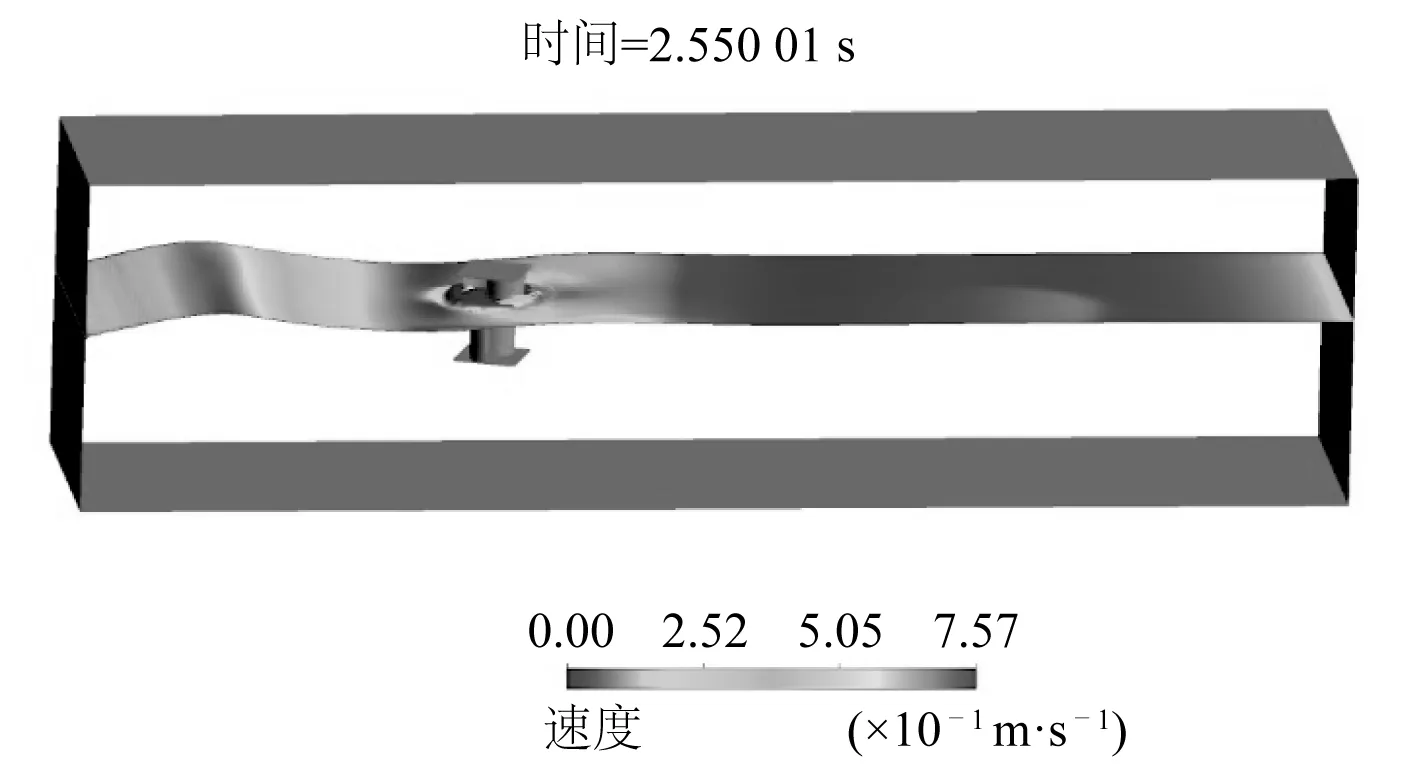
图6 水槽内部波浪运动Fig. 6 Wave motion diagram inside the sink

3.2 S型桨叶模型

对于被动型动网格计算问题，采用6DOF(Six Degrees of Freedom)动网格模型实现桨叶受波浪冲击转动，通过DEFINE_SDOF_PROPERTIES宏，定义桨叶质量及三方向惯性矩，限制其五个方向自由度，释放y方向自由度。采用六面体结构划分网格，网格节点数为84 700。为提高流体流经桨叶表面时计算精度，设置六层边界层，第一层网格高度为0.1 mm，高度膨胀率为1.2。

3.3 求解设置

为避免S型桨叶转动产生负体积网格，采用重叠网格的方法将桨叶添加在数值水槽内，将桨叶外部0.3 m处网格与流场内部网格建立重叠耦合面。保持波高0.2 m不变，在桨叶外侧0.02 m处设置波浪流速监测点，由式(11)计算桨叶叶尖速比。在Force Report里设置对桨叶的动转矩系数监测，由式(13)计算桨叶功率系数。这里数值模拟采用了基于压力的求解器及瞬态计算，采用Coupled算法及一阶迎风格式对控制方程进行离散化。残差收敛标准均设为1×10-5，时间步长0.005 s，最大迭代步数50步，迭代次数2 000。求解过程中，水槽内部波浪运动如图6所示。

为了研究重叠率、开口率和相对入水深度对S型桨叶功率系数的影响规律，设计仿真方案参数如表2所示。

表2 仿真方案参数Tab. 2 Simulation scheme parameters

3.4 试验对照分析

为了对仿真分析结果进行验证，进行了S型桨叶物理模型试验，试验场地如图7所示。试验水槽尺寸为10.0 m×0.6 m×1.0 m(长×宽×深)，在与仿真所用入射波高相同的条件下，检测并记录试验波高，数据对比如图8所示。

图7 试验场地及装置照片Fig. 7 Experimental site and device diagram

由图8可见，仿真分析与模型试验得到的功率系数之间最大相对误差不超过20%，验证了所建桨叶模型及所采用仿真分析方法的准确性。

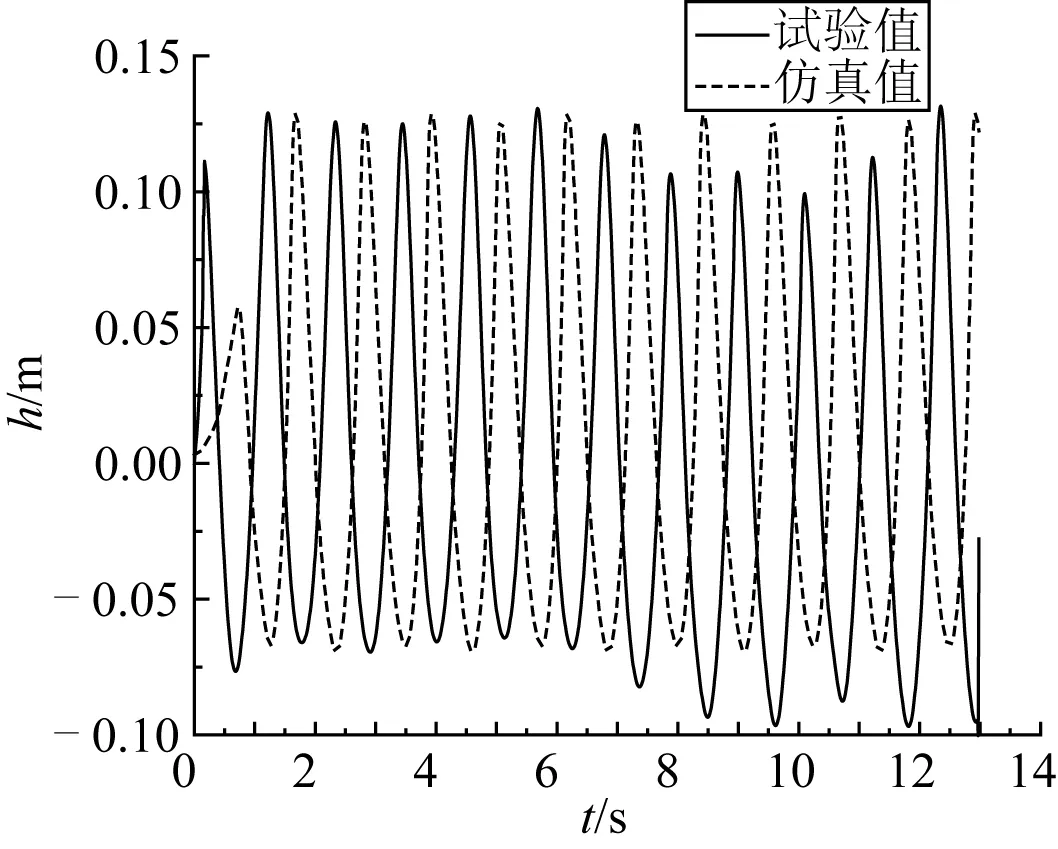
图8 波高监测对比曲线Fig. 8 Wave height detection curve

4 数值模拟结果分析

4.1 重叠率e对桨叶动转矩系数的影响

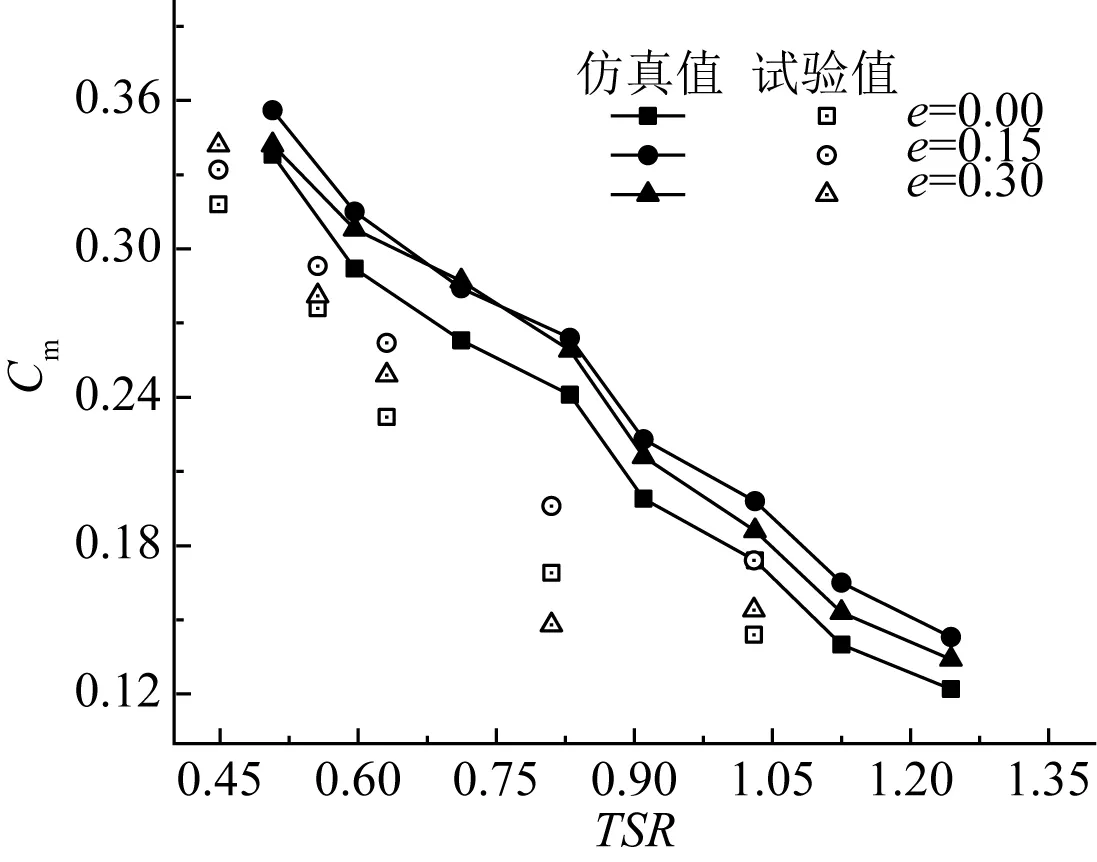
图9 动转矩系数-叶尖速比曲线Fig. 9 Dynamic torque coefficient-tip speed ratio curve

S型桨叶的水动力性能可用功率系数、动转矩系数和叶尖速比三个参数及其相互关系来描述。不同的结构参数及其不同的取值对桨叶性能会产生不同的影响。在重叠率e分别取值0.00、0.15、0.30时，仿真和物理试验得到的叶尖速比对转矩系数的影响关系如图9所示。可见，转矩系数随叶尖速比的增大而减小；重叠率的存在对转矩系数的提高有正面影响，但存在最佳值，如e=0.15时的转矩系数明显高于e=0.00和e=0.30时的转矩系数。由仿真得到的桨叶转动速度矢量图(图10)可以发现，对于有重叠部分的桨叶，水流通过中心通道流向凸叶片背部流域，增加了流体对桨叶的驱动力矩，有助于避免负转矩的产生。但当e=0.30时，由于开口过大，叶片端部出现涡流，阻碍了正向转矩的提高。

图10 桨叶转动速度矢量Fig. 10 Rotor rotation speed vector

图11 不同相对入水深度下水平波浪力-波高曲线Fig. 11 Horizontal wave force-wave height curve at different relative water inflow depths

4.2 相对入水深度l 对桨叶功率系数的影响

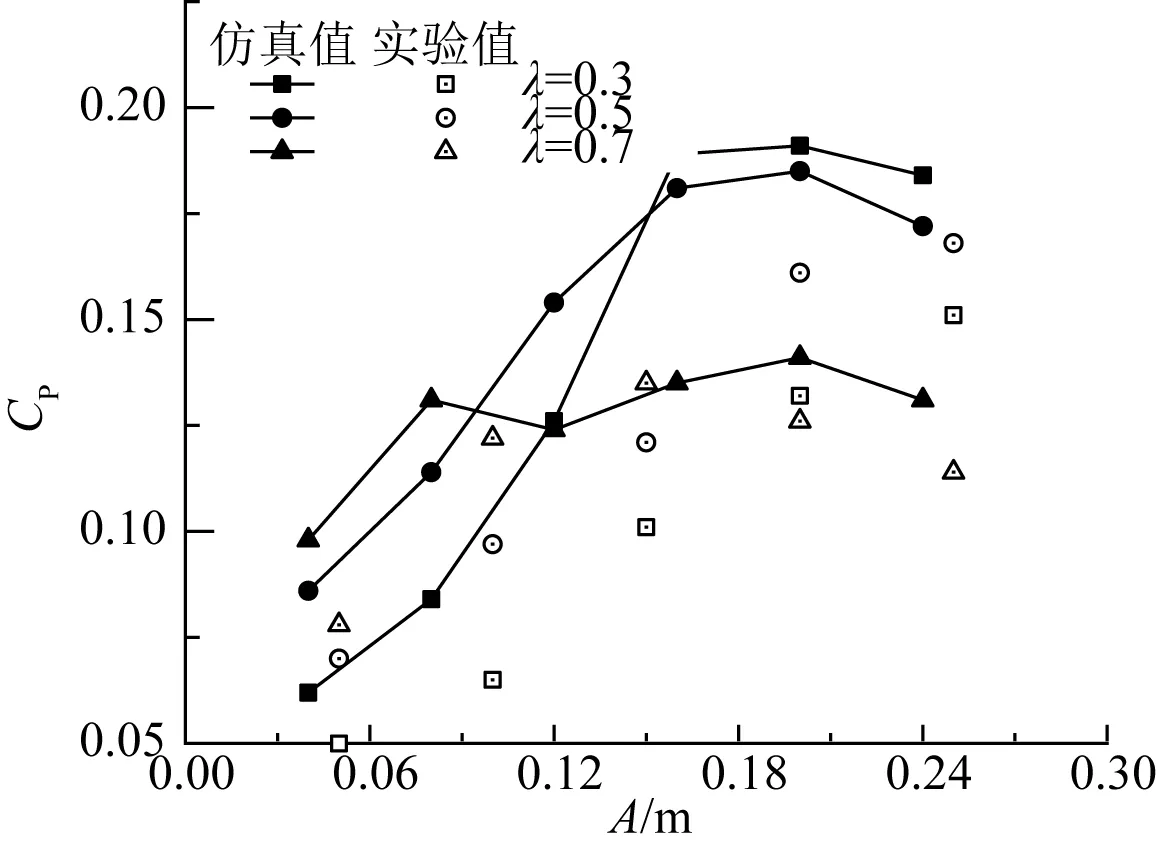
由于波浪能量主要集中在水面，桨叶相对入水深度与捕能效率密切相关。取水深h=1 m，波数k=1.5，桨叶高度H=0.4 m，由式(3)可得不同相对入水深度下水平波浪力与波高曲线，如图11所示。当A>h1即波浪越过桨叶时，波浪力随波高增大而增大的速率减缓；当A

在固定重叠率e为0.15情况下，调整桨叶在水面上高度以改变相对入水深度，通过仿真得到波浪高度h对功率系数CP的影响关系曲线，如图12所示。可见，在波浪未越过桨叶时，波浪高度h对桨叶功率系数CP影响较大，近似呈线性增长趋势；但波浪越过桨叶后，波浪高度h增加对功率系数CP影响不大，并略有减小。当波浪较小时，入水深度越大能量捕获效果越好；当波浪较大时，入水深度越大能量捕获效果越差，表明S型桨叶适合工作在波浪表面，桨叶在水面上高度与波高相等时，桨叶功率系数达到最大。因此随波浪高度变化调整桨叶相对入水深度，可获得最佳功率系数。在试验中，l=0.3、h=0.16时，能量捕获效果最优，功率系数达到最大值0.191。

4.3 开口率ε对桨叶动转矩系数的影响

在桨叶上设置一弹片阀，以提高桨叶动转矩系数。在运行过程中，当叶片处于“凸叶片”位置时，弹片阀打开，让部分海浪穿过阀口，减小凸叶片产生的阻力矩；当叶片处于“凹叶片”位置时，弹片阀关闭，使整个凹叶片都用于产生驱动力矩。取开口率ε分别为0、0.3、0.5，在流场速度v=0.6 m/s下，借助于Fluent和Static Structural软件工具对桨叶受力情况进行仿真分析，部分结果示于图13、图14。图13为弹片阀在波浪作用下的应变情况，图14为对应不同弹片阀开口率时桨叶动转矩系数随转角的变化曲线。

图12 不同相对入水深度下功率系数-波高曲线Fig. 12 Power coefficient-wave height curve at different relative water inflow depths

图13 v=0.6 m/s时弹片应变情况Fig. 13 Strain of v=0.6 m/s

图14 不同开口大小下动转矩系数-角度曲线Fig. 14 Dynamic torque coefficient-angle curve for different aperture ratios

由图14可见，在桨叶上安装弹片阀可有效减小负转矩，增大动转矩系数，且动转矩系数随开口率的增大而增大；开口率ε=0.5时的桨叶最大动转矩系数0.68比ε=0时的最大动转矩系数0.53提高28.3%。

5 结 语

利用数值仿真和试验相结合的方法研究了二阶S型桨叶水动力特性，提出了一种设置可调开口弹片阀的桨叶，研究了重叠率、相对入水深度对桨叶捕能效率的影响，得出结论如下：

1) 凹叶片与凸叶片的适当重叠可有效减小作用在桨叶上的负转矩，增大正向驱动转矩；重叠率对转矩系数的影响存在最佳值，重叠率过大将会在桨叶端部产生涡流，阻碍正向转矩的增加。

2) S型桨叶适合工作在波浪表面，其相对入水深度对桨叶捕能效率影响较大；桨叶在水面上高度与波幅相等时，桨叶功率系数达到最大。

3) 在桨叶上设置弹片阀开口，有利于增大动转矩系数，且弹片阀开口面积越大，效果愈加显著。试验分析结果表明，当弹片阀开口率为 0.5时，其动转矩系数比开口率为0时的桨叶提高28.3%。