隧道围岩稳定性改进模糊概率模型及其应用研究

陈子健, 闫自海, 2, 甘鹏路, 2, 左凯华

(1. 中国电建集团华东勘测设计研究院有限公司， 浙江 杭州 311122；2. 浙江省智慧轨道交通工程技术研究中心, 浙江 杭州 311225；3. 华夏幸福基业股份有限公司， 北京 100027)

0 引言

随着公路建设的不断发展和公路等级的不断提高，隧道建设规模和数量日益增多，隧道建设施工技术取得了显著的改进和突破。目前，我国公路隧道总里程已居世界首位[1]。隧道建设过程中，围岩稳定性是直接影响隧道工程造价的最主要因素。若不能较好地控制围岩位移、预防围岩塌方，将造成巨大的经济损失，甚至危及施工人员的生命，产生严重的社会不良影响。因此，正确合理地判别隧道稳定性对目前隧道失稳灾害防治和保障隧道安全施工及运营具有重大的意义和较高的工程应用价值。

目前，隧道围岩稳定性判别方法主要包括数值模拟法[2-3]、模型试验法[4]、现场监测法[5]等。由于数值模拟法所需的计算参数很难符合工程实际需求，且忽略了施工期间的人为因素，因此只能对围岩稳定性进行大致判别；模型试验法获取结果较好，但耗资巨大，且同样存在参数选取问题；现场监测法是以各工程规范[6-7]中位移判据为准则，采用现场监测围岩位移量及位移速率等数据判别围岩稳定性的方法。现场监测方法属于定值判别法，具有直观、准确的优点，在隧道施工中已得到广泛应用[8]。然而，确定位移判据因素复杂，从范围值中选取合适的定值较为困难，且量测结果存在的随机因素也不容忽视。更为重要的是实际工程中无法利用某一定值作为判别隧道是否稳定的依据，因此，这种定值判别结果往往不能反映工程实际情况[9]。考虑到隧道稳定性和位移之间存在的模糊不确定性以及隧道位移的随机不确定性，采用模糊概率方法代替定值法判别隧道围岩稳定性更为合理。

模糊事件的概率最早于1968年由Zadeh[10]提出，之后逐步发展为成熟的模糊概率理论[11]。该理论综合模糊理论和概率论将事件模糊性和随机性进行统一，目前已广泛运用于基坑[12]、路基[13]、边坡[14]等岩土工程领域，但在隧道稳定性方面运用并不多。国内最早是景诗庭等[9,15]建立了围岩稳定性模糊概率模型，将围岩稳定性问题数学化。申玉生等[16]利用双曲线函数和Boltzaman函数进行曲线回归分析，结合模糊概率方法对双连拱隧道围岩稳定性进行计算分析。许文锋等[17]将模糊概率模型引入海底隧道稳定性分析中，利用监测数据的回归分析并结合模糊概率模型得到了较合理的稳定性判别结果。然而，模糊概率模型的关键技术除了量测数据的整理之外，隶属函数的确定也尤为重要。而以上研究中隶属函数主要由规范[6-7]所给出的极限位移以及专家经验确定，且对隶属函数曲线作了线性简化处理。因此，该方法所确定的极限位移仅为一范围值，且具有一定的主观性；另外，对隶属函数的简化处理虽便于计算，但会对模糊概率模型的准确性产生负面影响。

鉴于此，本文引入RandWPSO-LSSVM极限位移模型[18]，对传统的隶属函数进行优化处理，并进一步对隧道围岩模糊概率模型进行改进，最后结合实际工程案例对改进模型进行验证，以期为隧道围岩稳定性评价提供一种更为可靠有效的分析手段。

1 传统围岩稳定模糊概率模型

1.1 模糊概率基本理论

基于模糊概率基本理论[11]，将围岩极限位移作为随机变量[19]，设在某一时刻围岩收敛位移为x，则可知隧道围岩保持稳定的概率[20-21]为

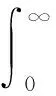
(1)

式中：p(x)为位移概率密度函数；μA(x)为位移对隧道稳定性的隶属函数。

1.2 概率密度函数的确定

基于模糊概率基本理论，认为围岩位移随时间t变化的过程是随机过程，围岩位移量为随机变量[20]，其概率密度函数可表示为

(2)

式中：u为某时刻围岩位移预测值；σ1为相应的标准差。

(3)

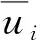
1.3 隶属函数的确定

为分析隧道稳定的模糊性，引入隶属函数表示围岩位移发展对隧道稳定的隶属程度，其为在[0, 1]闭区间的连续函数。假设当围岩位移小于极限位移量时，隧道不会发生失稳，稳定隶属度为1；当位移发展超过极限位移量上界时，围岩发生破坏失稳，其稳定隶属度为0。从概率与统计的角度看，该极限位移量为非定值，属于模糊随机变量，具有统计特征。假设统计所得的极限位移概率密度f(x)服从正态分布，其曲线如图1所示。

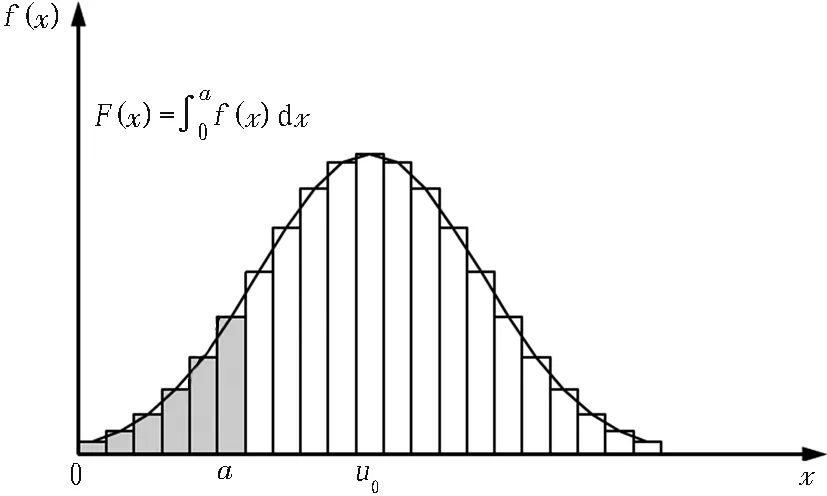
图1 围岩极限位移概率密度函数曲线

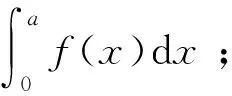
(4)

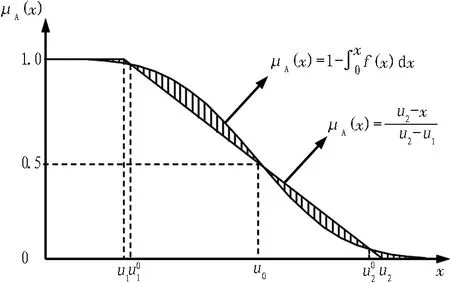
图2 隶属函数曲线

将图2中μA(x)曲线上±2σ0及中值3点连成1条直线，与上下2条渐近线交点为u1和u2，则隶属函数可以简化为

(5)

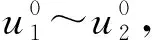
(6)

1.4 不足之处

将式(2)和式(5)代入式(1)中，即可推导求解隧道围岩稳定概率。然而，传统围岩稳定模糊概率模型中隶属函数的确定方法虽然具有一定的合理性，但仍存在以下2点不足：

1)国内外大量量测资料统计分析与专家经验判定的成果虽然规定了不同围岩级别和不同埋深下极限相对位移的取值范围，但埋深和围岩质量分级范围较宽，且未考虑隧道开挖尺寸以及施工因素等影响。

2)采用线性简化方法处理隶属函数会造成简化前后函数的取值存在偏差，且偏差随极限位移概率密度函数标准差的增大而增大。

以上2点不足将影响隶属函数的合理性及可靠性，继而造成整体概率模型与实际吻合度不高。同时，该模型仅适用于评价围岩预测位移的稳定概率，无法对围岩实测位移进行稳定性分析。

2 围岩稳定改进模糊概率模型

2.1 RandWPSO-LSSVM极限位移预测模型

RandWPSO-LSSVM极限位移预测模型[18]是基于随机权重粒子群算法(RandWPSO)-最小二乘支持向量机(LSSVM)的预测模型。该模型采用工程类比法，通过收集已有地下工程围岩的极限位移数据作为测试和检验样本，并综合考虑隧道形状、尺寸、埋深、围岩级别等因素预测模型的可靠性[21]。

根据RandWPSO和LSSVM算法的原理和特点[22]，得到极限位移的RandWPSO-LSSVM预测模型流程如图3所示。图3中，σ为核函数，C为惩罚因子，是LSSVM模型的重要参数；Pbest和gbest分别表示个体最优解和全局最优解。

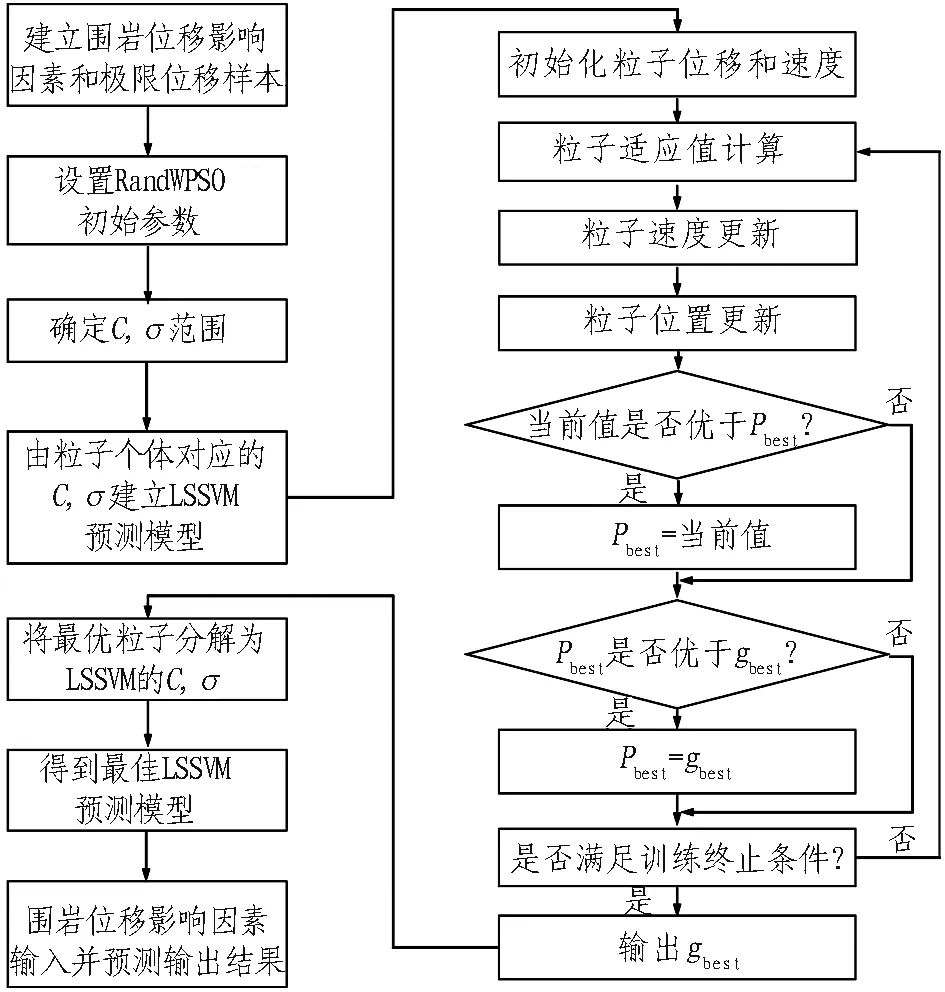
图3 极限位移RandWPSO-LSSVM预测模型流程

Fig. 3 The flow of RandWPSO-LSSVM prediction model of limit displacements

表1示出基于实际工程所获取的围岩极限位移学习及测试样本。其中，将样本编号1—36作为学习样本，37—42作为测试样本。对该样本进行机器学习可得到最佳的模型参数，从而建立RandWPSO-LSSVM预测模型，再将测试样本代入该模型即可得到预测值。其极限位移最大预测相对误差为6.72%，误差较小，表明该模型具有较好的预测效果。

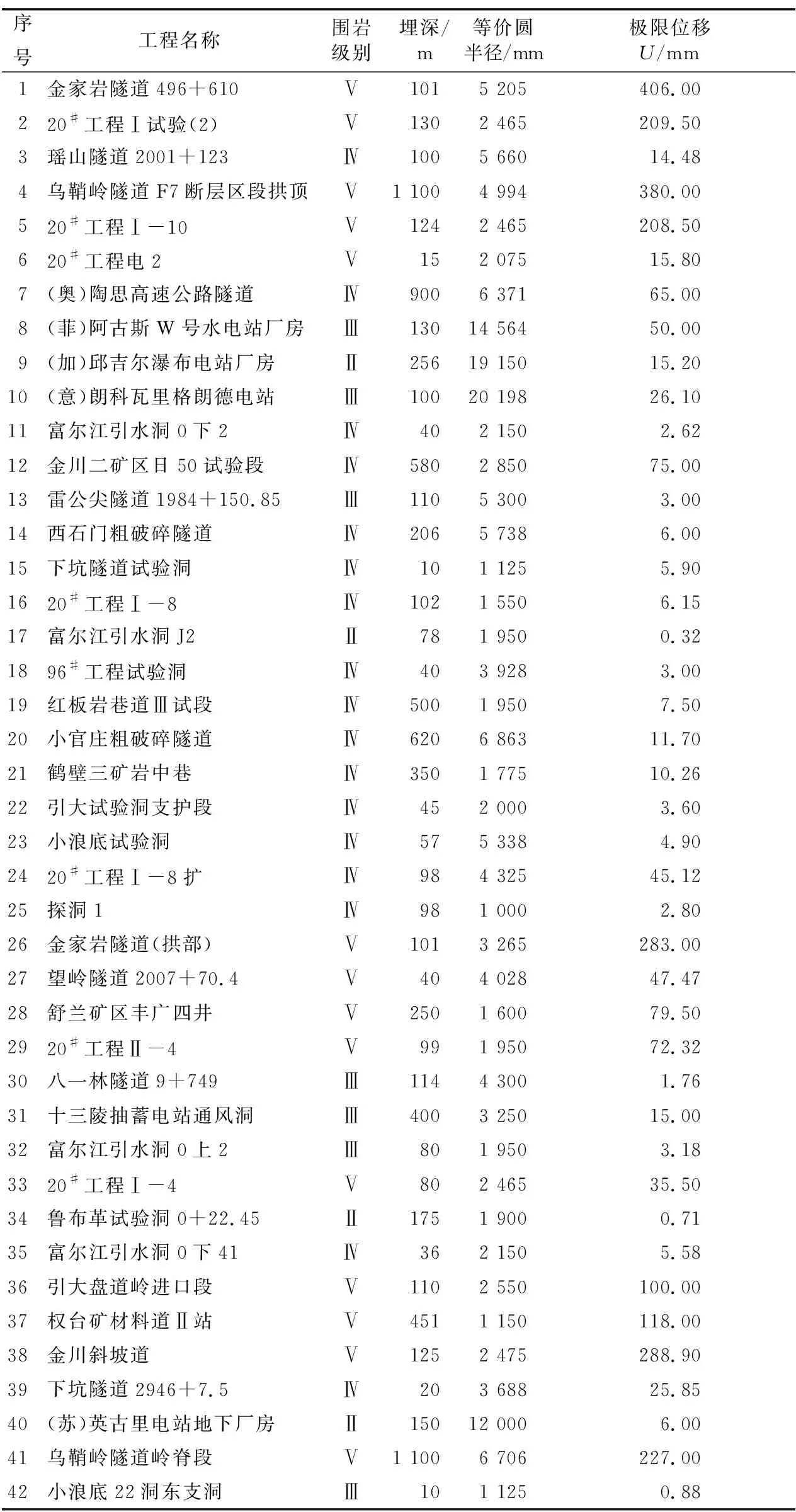
表1 围岩极限位移学习及测试样本

2.2 改进隶属函数

由1.3节可知，从概率与统计的角度看，极限位移量为非定值，而是模糊随机变量，具有统计特征，其概率密度函数如图1所示。引入RandWPSO-LSSVM极限位移预测模型，根据位移概率密度函数确定方法，得到极限位移概率密度函数为

(7)

式中：U为围岩极限位移预测值；σ2为相应的标准差。

回归模型预测值与实测值之差可近似为正态分布，故有

(8)

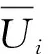
各位移量对隧道稳定性的隶属函数为

(9)

2.3 改进围岩稳定概率模型

将式(2)和式(9)代入式(1)中，有

(10)

化为常规二重积分形式，即

(11)

式(11)为对预测位移值进行稳定性计算的概率模型。为及时掌握隧道围岩稳定程度，控制隧道变形，实测位移稳定概率计算同样重要。设某时刻实测位移为a，该事件为已发生事件，故无需讨论其概率密度函数，即可将隧道围岩稳定问题转化为一个常规的随机事件概率问题。由式(4)可知

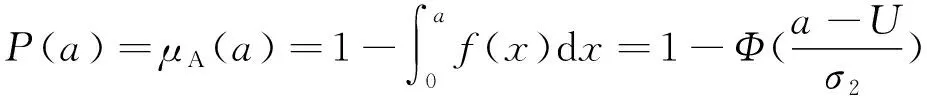
(12)

对式(12)进行反解，可求得特定稳定概率所对应的隧道位移a。

式(11)和式(12)均可采用Matlab进行编程计算。基于u、σ1、U及σ24个相关参数即可求得隧道围岩稳定概率。

3 改进模型验证

为验证围岩稳定改进模糊概率模型的合理性及优越性，通过查阅文献及相关调研[19, 23-26]，选取8个隧道算例，采用第2节所述的RandWPSO-LSSVM模型进行极限位移预测，各算例隧道工况参数如表2所示。

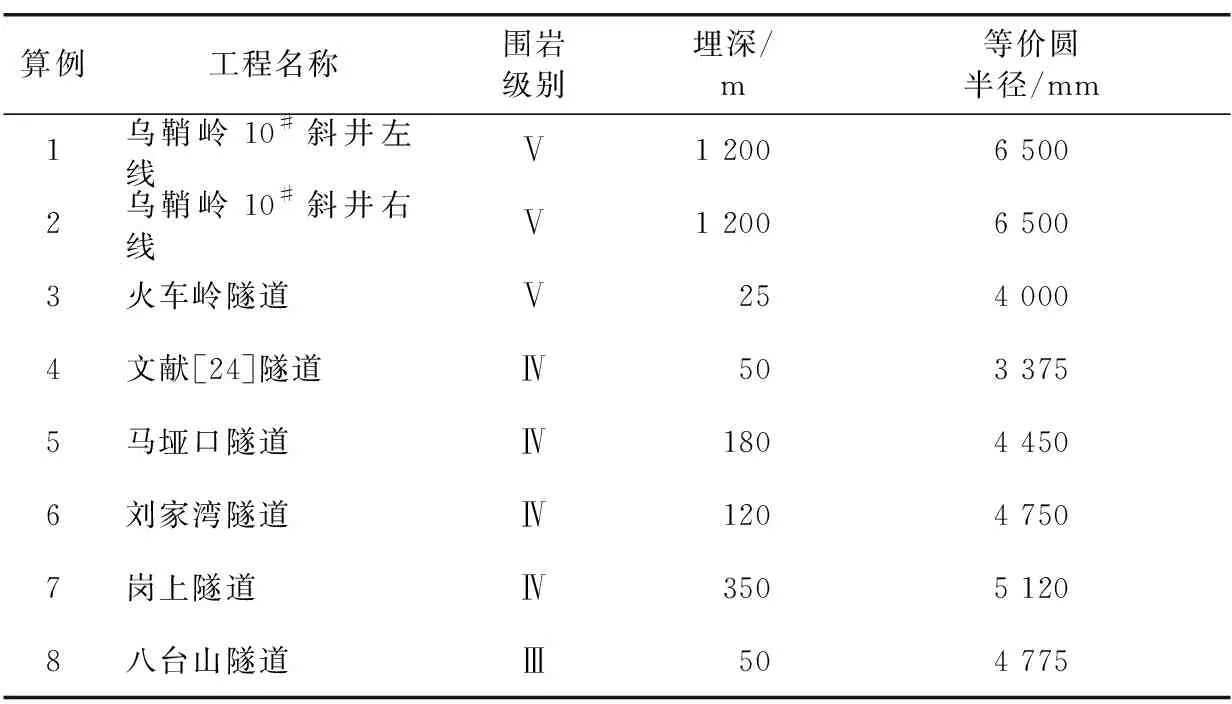
表2 各算例隧道工况参数

3.1 传统模型下围岩稳定概率计算

对于算例1—4，前人已用传统模糊概率模型进行详细分析，并已求得工程稳定概率。对于算例5—8，由1.2节可知，预测位移标准差σ1需结合详细的围岩位移时序数据并进行回归曲线分析获取，而在该4个算例中围岩位移监测数据缺失，故无法确定σ1的值。但由式(2)和式(11)推理可知，在其余参数一定的条件下，σ1不会影响2种模型所得稳定概率的大小关系。为论证该推论，取多组参数分析不同σ1及u条件下2种模型围岩稳定概率的大小关系。

3.2 改进模型下围岩稳定概率计算

为计算表2中各算例在改进模型下的稳定概率，需事先确定各算例参数U和σ2。由式(8)可知，预测样本数越多，所得σ2越符合工程实际，故本文选取表1中样本1—30作为学习样本，样本31—42作为预测样本，并建立RandWPSO-LSSVM模型。样本31—42围岩极限位移预测结果如表4所示。将表4中数据代入式(8)，可得σ2=4.09 mm。限于样本数量，σ2的取值可在丰富样本数据后作进一步的修改完善，本文暂以该值作为极限位移预测标准差。

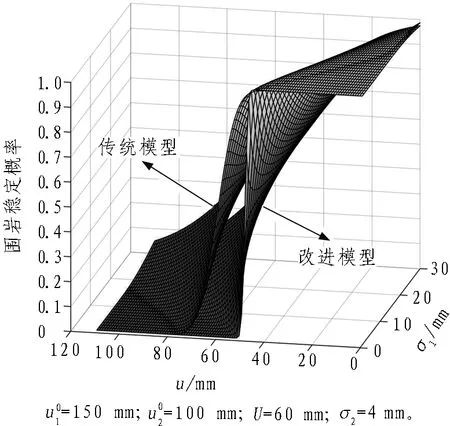
(a) 传统模型稳定概率>改进模型稳定概率

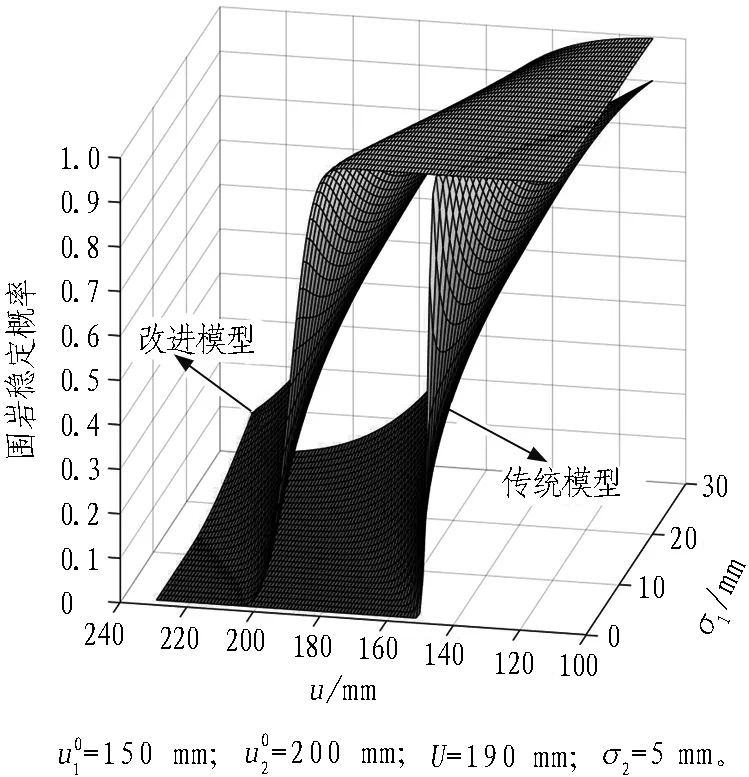
(b) 改进模型稳定概率>传统模型稳定概率

Fig. 4 Probability nephograms of surrounding rock stability of two models under differentσ1andu

已知各算例工况参数(见表2)，将其代入已建立的RandWPSO-LSSVM模型即可得出各算例的极限位移预测值U，结果如表3所示。U和σ2的取值确定后，结合已知参数u、σ1，由式(11)即可计算基于改进模型的围岩稳定概率，计算结果见表3。

3.3 计算结果对比分析

4 改进模型的应用验证

某高速公路隧道为3车道大跨度特长隧道，左右2洞均设有5个紧急停车带(加宽带)。在二次衬砌的浇筑进度到达加宽带时，施工单位综合考虑了安装设备的局限性、施工进度以及经济效益等因素，选择跳过加宽带继续浇筑普通带的方式推进施工，由此延缓了加宽带二次衬砌的浇筑时间，使得加宽带初期支护暴露时间过长。因此，分析加宽带监测数据并进行稳定性评价对于预防及控制该隧道失稳具有重要的工程意义。

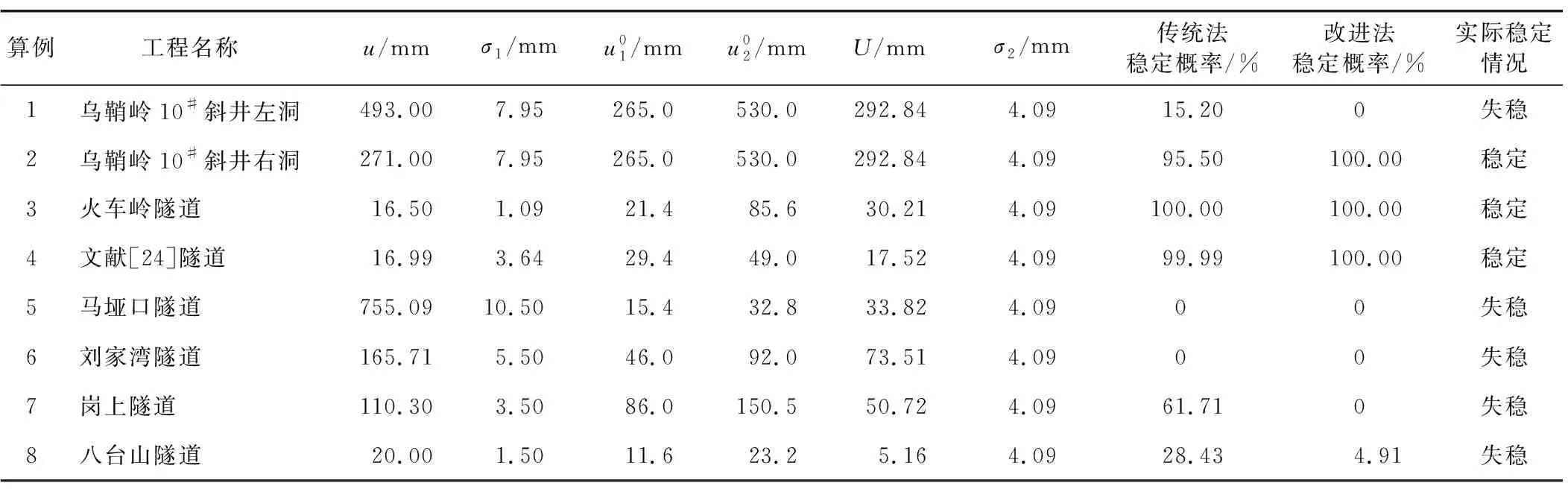
表3 2种模型下各算例的计算参数值及稳定概率计算结果

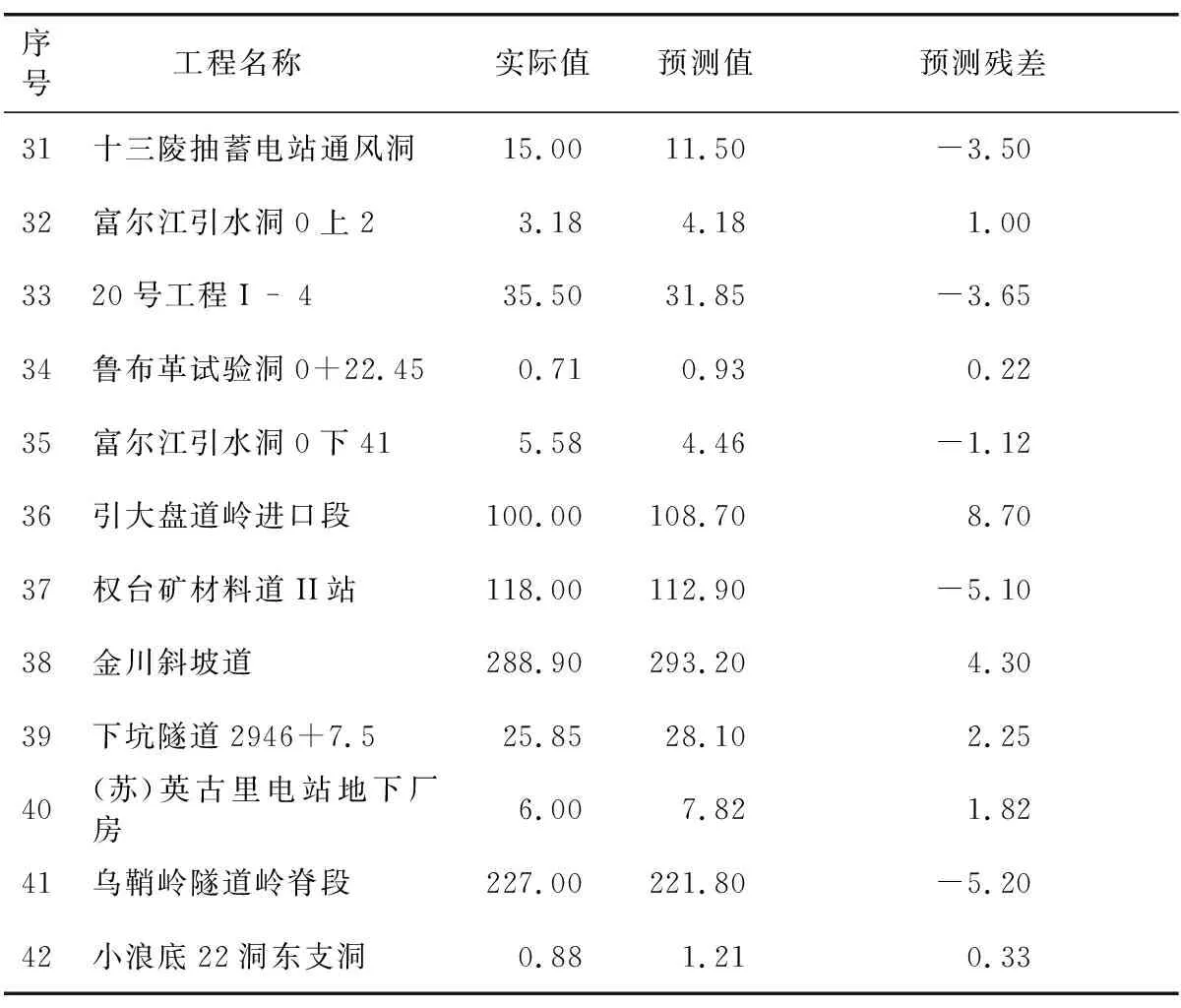
表4 样本31—42围岩极限位移预测结果

本文选取隧道右线入口段第2个加宽带(K24+864～+904)中K24+878断面的水平收敛数据作为分析对象。该断面开挖跨度为17.5 m，高8 m，埋深250 m左右，穿越东翼岩溶槽谷三叠系中统雷口坡(T2I)和三叠系下统嘉陵江组(T1j)地层，岩性主要为薄中厚层状的白云质灰岩、灰岩、角砾状灰岩、盐溶角砾岩等。隧道围岩较完整，但节理发育，局部岩溶角砾岩段围岩较破碎，稳定性较差，围岩等级为Ⅳ级。隧道岩石物理力学参数见表5。

工程实践中，一般可采用不同拟合函数对现场监测数据进行回归分析，比较其回归精度。本文选取回归精度较高的指数函数对K24+878断面30 d的水平收敛数据进行回归分析，结果如图5所示。

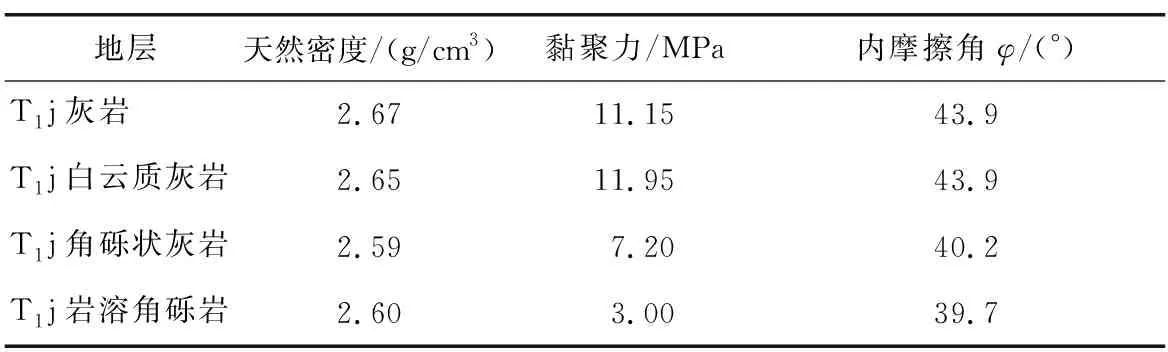
表5 隧道岩石物理力学参数

图5 K24+878断面水平收敛时态曲线

由图5可知，K24+878断面水平收敛时态曲线的回归方程为

(13)

其相关系数为0.993 4。根据回归方程式(13)计算第60天隧道的位移为25.95 mm，将该位移作为预测极限位移； 同时将该预测位移标准差按照式(3)进行求解，得σ1=1.18 mm。

将所获取的参数u、σ1、U和σ2的值(见表6)代入式(12)，即可求得K24+878断面围岩稳定概率为99.98%。

综上所述，由预测结果表明该高速公路隧道K24+878断面在开挖第60天时保持稳定概率为99.98%，稳定性较高，可根据洞内实际情况适当降低监测频率。对于该隧道围岩实测位移稳定性评价，本文根据其稳定概率大小拟将围岩稳定等级分为5级(见表7)。已知U=41.52 mm、σ2=4.09 mm，按照式(13)编写Matlab程序反算求得表7中位移范围。监测过程中，将隧道实测位移与表7进行对照，可总体评价该高速公路隧道围岩的稳定程度，便于制定并及时采取相应的隧道预警及工程处治管理措施。

表6 K24+878断面工况参数及极限位移预测结果

Table 6 Working condition parameters and limit displacement prediction results of examples at section K24+878

断面围岩级别埋深/m等价圆半径/mm极限位移U/mmσ2/mmK24+878Ⅳ2506 17541.524.09

表7 K24+878断面围岩稳定分级

Table 7 Stability classification of surrounding rock at section K24+878

稳定等级稳定概率/%位移范围/mm稳定>80<37.32比较稳定60～8037.32～40.26中等稳定40～6040.26～42.79稳定性较差20～4042.79～45.73不稳定<20>45.73

5 结论与展望

模糊概率分析法综合考虑了隧道围岩变形的模糊不确定性和随机不确定性，但现有研究中针对围岩稳定性建立的模糊概率模型隶属函数仍存在一定的缺陷。本文引入RandWPSO-LSSVM围岩极限位移预测模型，对隶属函数进行优化，建立改进后的围岩稳定性模糊概率模型。主要结论如下。

1)改进模型解决了传统隶属函数存在的极限位移取值范围不合理的问题，有效消除了因隶属函数简化处理导致的误差，并明确了对隧道围岩实测位移评价的稳定概率计算方法，有利于现场施工中根据监测数据及时掌握隧道围岩稳定程度，控制隧道变形。

2)基于改进模型公式，编写了Matlab计算模型，基于参数u、σ1、U和σ2即可求解隧道围岩稳定概率； 并将改进模型与传统模型的计算结果进行对比，结果表明改进模型得出的稳定概率与实际情况吻合较好，可提高隧道围岩稳定性评价的可靠性。

3)采用改进模型对某隧道右线K24+878断面围岩进行稳定性分析。结果表明，该断面围岩极限位移为41.52 mm，第60天稳定概率为99.98%，稳定性较高，且与现场实际观测结果吻合。同时，提出了用于控制隧道变形的位移管理预警标准。因此，运用该模型对隧道围岩稳定程度进行量化评价可作为保障现场安全顺利施工的有效手段之一。

综上，基于极限位移预测模型建立的改进模型，其可靠性取决于模型的预测精度，U和σ2取值越合理，模型所得的稳定概率越符合实际。因此，增加RandWPSO-LSSVM模型中学习样本和影响因素的数量以及开发更科学合理的极限位移预测模型，都有待于进一步的研究和完善。