一种角度融合算法在姿态角解算中的应用
2020-05-08张振涛
张振涛,王 娟
(1.吉林化工学院 信息与控制工程学院,吉林 吉林 132022;2.吉林工业职业技术学院 电气与信息技术学院,吉林 吉林 132013)
水准仪从过去的气泡式到现在的电子式经历了几代的改进[1],在其姿态角数据测量中,传感器测量的数据需要进行标度转换成实时的角度显示.而角度融合算法在工程上的实现有不同的方法,采用欧拉角微分方程式需要进行三角函数的运算,且方程会出现“奇点”,方程式退化,所以不能全姿态工作[2];用方向余弦法计算姿态矩阵,没有方程退化问题,可以满足全姿态工作,但是需要求解六个微分方程,计算量较大,影响嵌入式系统的响应时间[3];Rodrigue参数法计算效率较高,且结构简单直观,但是存在旋转角有奇异值的缺陷[4].采用四元数微分方程式,通过建立水平仪达到嵌入式系统,验证该方法在该系统的应用.
1 测量方法
四元数微分方程式是惯性导航技术中常用的数学工具[5].四元数是简单的超复数,由一个实部加上单个虚部构成,可以表示为a+bi+cj+dk,其中a、b、c、d都是实数.在惯性系统中,在一个三维空间内用四元数描述目标相对一个固定坐标系的方向矢量,其中标量部分代表了转角一半的余弦值,也就是转角的大小,而矢量部分表示相对于坐标轴的转动方向,也就是瞬时转动轴和坐标系之间的方向余弦值.
可以通过四元数求出一个物体相对于参考坐标系旋转之后的坐标信息,那么参考坐标系和旋转后的坐标系的转换关系用变换矩阵式(1)来解算.
(1)
其中q1是四元数的实部,q2、q3、q4是四元数的虚部.
物体旋转过后相对参考坐标系的角度变化信息可以通过复合绕X轴旋转称物体的翻滚角(θ)、绕Y轴旋转称物体的俯仰角(γ)、绕Z轴旋转称物体的航向角(ψ)得到三个姿态角的变换矩阵复合得到物体相对于参考坐标系的角度信息,姿态角变换矩阵如式(2)所示.
(2)
(3)
式(1)物体转动的姿态变换矩阵和式(3)物体绕三轴旋转复合的姿态角矩均为参考坐标系变换到物体坐标系的姿态矩阵,所以两变换矩阵相等,也就是两个变换矩阵元素一一对应相等[6].取第3行3个元素分别为g1、g2、g3和第1列第2个元素为g4,第1列第1个元素为g5则有:
根据以上方程组,知道了q1、q2、q3、q4的具体数值,就能求出需要的姿态角.
2 测量电路
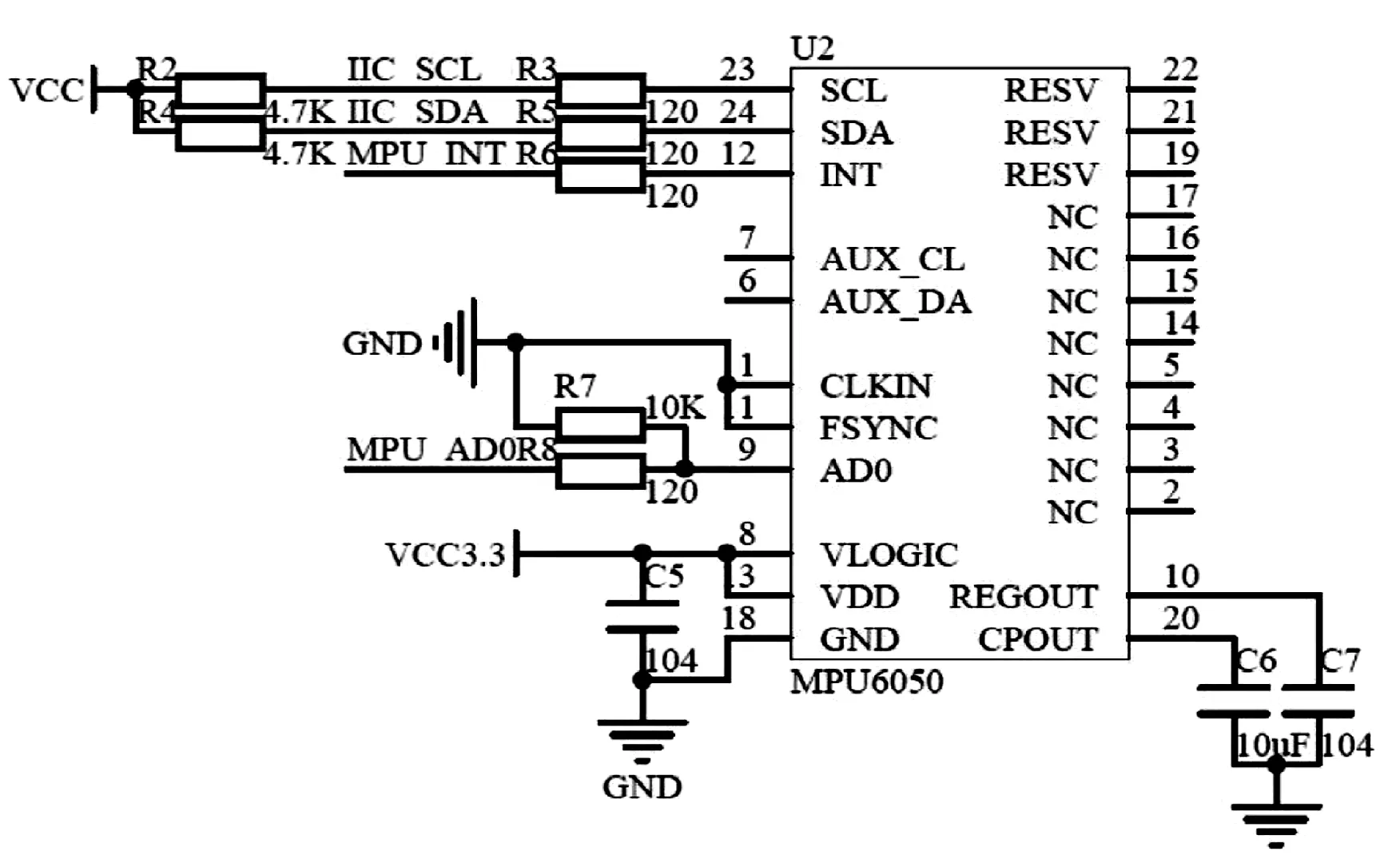
图1 测量电路图
MPU6050使用I2C或者SPI接口和芯片连接,并且总是作为从设备.本系统采用I2C接口,而且使用模拟I2C协议,因此单片机引脚的驱动能力一般不够,所以SDA和SCL信号线通常需要接上拉电阻到VDD来增加驱动能力,如图1所示.读取芯片的数据先要进行初始化,需要配置电源管理、陀螺仪采样频率、低通滤波频率、陀螺仪自检及测量范围和加速计自检、测量范围及高通滤波频率.初始化之后就可以读取各轴的数据,每轴的数据是16位,分高8位和低8位,高字节地址在前,低字节地址在后.
从MPU6050读出的数据要进行卡尔曼滤波之后将数据进行矩阵运算得到四元数[7],再将四元数通过反三角函数计算得到当期那的角度.
3 软件实现
如果现在已知MPU6050测得的角速度和加速度,那么需要求解一个四元数微分方程,通过求解微分方程,就可以得到我们需要的四元数参数.求解过程要对角速度进行积分,积分过程中角速度误差会加大,所以我们需要用加速度信息来校正角度信息,从而减小误差.
在MCU也很容易实现,首先定义四个浮点数q1、q2、q3、q4,将经过滤波后的数据单位化,接下来估计重力方向,同时将把四元数换算成方向余弦矩阵中第3列的3个元素,同样需要定义浮点数类型的vx、vy、vz、ex、ey、ez.
vx=2*(q1q3+q0q2);
vy=2*(q0q1+q2q3);
vz=q0q0-q1q1-q2q2+q3q3;
ex=(ay*vz-az*vy);
ey=(az*vx-ax*vz);
ez=(ax*vy-ay*vx);
其中ax、ay、az是MPU6050读取的数.ax、ay、az是固定坐标参照系上加速度计测出来的重力方向的向量,vx、vy、vz是陀螺仪对角速度积分后的重力方向的向量,它们之间存在的误差可以用向量叉积来表示,ex、ey、ez就是两个重力向量的叉积,这个叉积向量仍旧是位于坐标系上的,陀螺积分误差也是基于这个坐标系,叉积的大小与陀螺积分误差正好成正比,故拿来纠正陀螺[8].根据MPU6050的读取速度跟单片机的运算速度需要再定义delta_2和FACTOR,用来校正陀螺仪测量值,同时用叉积误差来做PI修正陀螺零偏,最后整合四元数率,利用四元数微分方程,使用的是二阶毕卡法.
delta_2=(2*halfT*gx)(2*halfT*gx)+(2*halfT*gy)(2*halfT*gy)+(2*halfT*gz)(2*halfT*gz);
q0=(1-delta_2/8)q0+(-q1*gx-q2*gy-q3*gz)halfT;
q1=(1-delta_2/8)q1+(q0*gx+q2*gz-q3*gy)halfT;
q2=(1-delta_2/8)q2+(q0*gy-q1*gz+q3*gx)halfT;
q3=(1-delta_2/8)q3+(q0*gz+q1*gy-q2*gx)halfT;
其中gx、gy、gz是MPU6050读取的数.正常化四元数后,换成当前的欧拉角.
Q_ANGLE.Y=asin(-2*q1*q3+2*q0*q2)*57.3;
Q_ANGLE.X=atan2(2*q1*q2+2*q0*q3,-2*q1*q1-2*q2*q2+1)*57.3;
Q_ANGLE.Z=atan2(2*q1*q2+2*q0*q3,-2*q2*q2-2*q3*q3+1)*57.3;
到此就完成了从加速度计和陀螺仪的数据向角度的转换,本实验装置只用到了其中两个角度X和Y,只需要计算其中两个.
4 调试与实验
实验由STM32单片机做主控芯片,配合MPU6050传感器、无线收发模块、液晶显示模块、上位机通讯电路和电源完成对数据的采集、处理、无线通讯以及显示,实物如图2所示.

图2 测量实物图
下位机通过串口将数据传送到上位机,本系统上位机编程环境是VC++2010[9],并且使用OpenGL设计3D模型.上位机对数据进行处理在界面显示.程序运行时,首先点击连接设备,成功后会有弹窗提示,串口号和波特率都是规定好的,当然在程序里可以改,连接成功后X和Y的数值会随着测量模块的变化而不断变化,点击立体图就会弹出另一个界面,如图3所示,它是将当前的角度用3D模型展现出来.
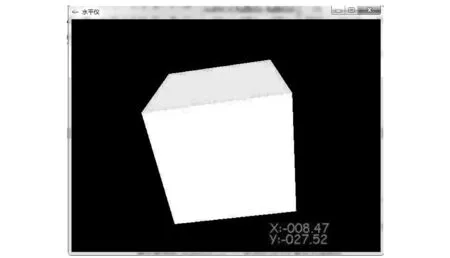
图3 模型显示界面
5 结 论
结合实际验证了四元数微分方程这种角度融合算法在姿态角解算中的应用,通过设计水准仪的测量装置,测量了平面的X轴和Y轴的角度,并且给出了四元数微分方程具体应用过程,减少了工程设计中工作量,简化了编程,而且提高了MCU的代码运行效率,以及水准仪的精度和稳定性,优化了显示界面,使显示不再固定,整个界面显得更加美观.
