一类四维时滞前馈神经网络模型的Hopf分支
2020-05-08王殿宏王文龙
王殿宏,王文龙,李 雪
(东北林业大学 数学系,哈尔滨 150040)

图1 四维前馈神经网络Fig.1 Four-dimensional feed-forward neural network
近年来,神经网络因其在模式识别、联想记忆、组合优化、自动控制等领域的广泛应用,受到越来越多的关注.神经网络的相关研究始于20世纪40年代.1943年,美国Mcculloch和Pitts首先提出了一种神经元的数学模型,即MP模型[1].1982年,美国物理学家Hopfield提出了Hopfield神经网络(HNN)模型[2].后来,许多学者提出并研究了大量的神经网络模型,并取得了显著成果,如细胞神经网络和双向联想记忆等[3-4].
随着生物学、神经网络等领域研究的不断深入,时滞动力系统的相关理论被广泛应用到这些领域中[5-7].由于外界干扰和信息处理速度有限,动力系统不可避免地存在时滞,时滞是影响系统动态行为的一个关键因素.而动力学系统除了研究稳定性[8-9]外,还可研究其它动力学行为,如振荡、混沌、多周期和不稳定等[10].因此,许多科研工作者相继对时滞神经网络的动力学行为进行研究[11-12].魏俊杰等[13]研究了具有时滞的二维网络神经模型的分支,王春梅等[14]研究了一类具有时滞的三维神经网络模型的分支与稳定性,李秀玲[15]研究了具有时滞的四维神经网络模型的分支问题,本文对图1所示的四个神经元的前馈神经网络模型进行研究.
由图1,可建立如下方程:
(1)
其中ui(t)(i=1,2,3,4)表示第i个神经元t时刻的活跃状态,a,b为连接权值,τ≥0表示神经元传输时滞.关于活跃函数f,在本文中假定:
(H1)f∈C1,f(0)=0,f′(0)=1;
在(H1)的条件下,系统(1)在平衡点(0,0,0,0)的特征方程为:
(2)
其中Δ1=λ+1-(a+b)e-λτ,Δ2=λ+1-ae-λτ.
本文主要研究内容如下:针对模型(1),利用中心流形定理和规范型理论,讨论了该模型产生Hopf分支的条件,假设输出函数为双曲正切函数,以μ作为分支参数计算其产生Hopf分支的直到三次项的约化规范型,并研究了Hopf分支周期解的稳定性及分支方向;最后通过数值模拟仿真,对理论结果进行了验证.
1 Hopf分支存在性
定理1 如果(H2)a+b<-1,-1 i) 当τ∈[0,τ0)时,系统(1)在平衡点(0,0,0,0)处是局部渐近稳定的. ii) 当τ=τj(j=0,1,…)时,系统(1)在平衡点(0,0,0,0)处产生Hopf分支,其中: 证明i) 当τ=0时,那么特征方程(2)的根分别为λ1=a+b-1<0和λ2=a-1<0,即平衡点(0,0,0,0)渐近稳定. 所以,当τ∈[0,τ0)时,Δ1=0的根都具有严格负实部. 综上可得,当τ∈[0,τ0)时,特征方程(2)的根都具有严格负实部,即系统(1)在平衡点(0,0,0,0)处是局部渐近稳定的. ii) 由Hopf分支产生的条件可知,当τ=τj(j=0,1,2,…)时,系统(1)在平衡点(0,0,0,0)处产生Hopf分支. 假设输出函数为双曲正切函数,将其作为神经元的触发非线性函数.即:f(·)=tanh(·). 则系统(1)变为: (3) 定理2 假设条件(H2)成立,当τ=τ0时,以μ为分支参数,系统(3)在平衡点(0,0,0,0)处产生Hopf分支的直到三次项的约化规范型为: (4) 则系统(3)可写为: (5) 对于φ∈C,定义: (6) 其中η是定义在[-1,0]上的有界变差函数矩阵,令η(θ)=τAδ(θ)+τBδ(θ+1),δ(θ)是Dirac delta函数,则: 通过计算可得: 将相空间C分解为:C=P⊕Q,其中Q={φ∈C|(ψ,φ)=0,ψ∈P*}.在扩充相空间BC中,系统(5)可以写成抽象的常微分方程: (7) 其中A是无穷小生成元A0的延拓[17]. 定义投影映射π:BC→P,满足: π(φ+X0α)=Φ[(Ψ,φ)+Ψ(0)α]. (8) 则空间BC可分解为:BC=P⊕kerπ,于是系统(7)可写成: (9) 其中x∈C2,y∈Q1=Q∩C1⊂kerπ,C表示复数域. 令u=Φx+y代入系统(9)并展开可得: (10) 其中: (11) 其中: 由式(11)可知: μx1e1,μx2e2 在中心流形中,方程(10)可写为如下形式的规范型: (12) 所以,系统(3)在平衡点(0,0,0,0)处产生Hopf分支的直到三次项的约化规范型为式(4). 令x1=r(cosθ-isinθ),x2=r(cosθ+isinθ),并忽略高阶项,则系统(4)可以写成: (13) 根据文献[18],得到以下定理. 定理3 如果-并且μ足够小,则: (14) 是系统(13)的周期轨道. 定理4 对于系统(13), i) 当μ<0时,原点是渐近稳定的; ii) 当μ>0时,原点是不稳定的;且此时产生渐近稳定的周期解. 针对系统(3)产生Hopf分支的情形进行数值模拟.取a=-0.5,b=-0.6时,条件(H1),(H2)成立,系统(3)在平衡点(0,0,0,0)处产生Hopf分支.计算得,ω0=0.458 3,τ0=5.917 8. 取μ=-1.417 8<0,则τ=τ0+μ=4.5时,由定理4可知,此时平衡点(0,0,0,0)是局部渐近稳定的,如图2. 取μ=0.082 2>0,则τ=τ0+μ=6,由定理4可知,此时平衡点(0,0,0,0)是不稳定的,如图3;并且此时会产生渐近稳定的周期解,如图4. 图2 τ=4.5<τ0=5.178,平衡点(0,0,0,0)局部渐近稳定Fig.2 The local asymptotic stability of equilibrium point(0,0,0,0)when τ=4.5<τ0=5.178 图3 τ=6>τ0=5.9178,系统(3)出现周期解Fig.3 The periodic solution of system (3) when τ=6>τ0=5.917 8 图4 系统(3)周期解的稳定性Fig.4 Stability of periodic solution of system (3) 本文研究了一类四维时滞前馈神经网络模型(1),对该模型产生Hopf分支的情形进行讨论,利用中心流形定理和规范型理论,以μ为分支参数计算相应的规范型,得到了系统产生Hopf分支周期解的条件,并给出了分支周期解稳定性及分支方向的判别条件.最后,通过计算机数值模拟仿真,对理论结果进行了验证.
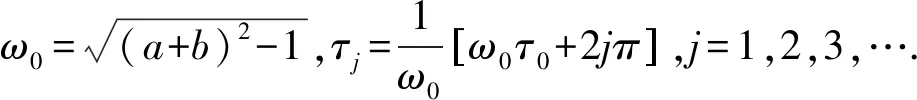
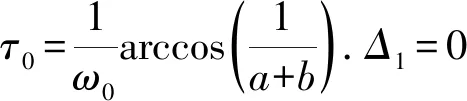
2 Hopf分支规范型




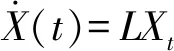






3 数值模拟



4 结语
