一类线性半向量二层规划问题全局最优解的搜索算法

王 媛，吕博慧，吕一兵*

(1.长江大学 信息与数学学院，湖北 荆州 434023； 2.中央电视台财经频道，北京 100020)

0 引言

近年来，二层规划在工程设计、交通、管理等领域应用广泛[1-3]，并且其研究价值也越来越高[4-5].半向量二层规划是上层为标量优化，下层为向量优化的一类二层规划问题[6].

对于线性半向量二层规划问题， Lü Y B等[7]采用下层问题的最优值转化方法设计了原问题近似最优解的算法；随后，吕一兵等[8]以下层问题的对偶间隙为罚项，构造了原问题的罚问题，并设计了相应的罚函数算法.对于非线性半向量二层规划问题， Ren A H等[9]在Benson方法和线性规划对偶理论的基础上，将原问题转化为单层问题进而设计了罚函数算法；Dempe S等[10]采用最优值转化方法将原问题转化为二层单目标规划问题，同时基于非光滑优化问题的最优性条件[11-13]得到了原问题最优解的一阶必要性条件，然而遗憾的是文献[10]并没有给出数值算法；Gadhi N等[14]由非光滑Mangasarian-Fromowitz约束规格给出了等价的单层优化问题，进而得到了原问题的最优性条件.

一般而言，在半向量二层规划问题中，对于给定的上层决策变量，其下层问题往往有多个最优解.在本文采用乐观最优解[15]，其数学模型可以表述为：

(1)

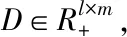
在问题(1)中，下层问题为:

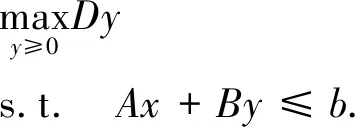
(2)

在接下来的内容中，将设计问题(1)的极点搜索算法[16].其基本思路是首先采用标量化方法将问题(1)转化为一般的二层规划问题，通过对偶原理给出问题(2)的最优性条件；然后用该条件代替问题(2)，进而将原问题转化为单层规划问题；随后基于所得到的单层规划问题可行域的基本性质，建立可行域顶点与最优解之间的关系，并给出相应的顶点搜索算法，最后给出算例来验证所设计算法.

1 相关定义及理论结果

S={(x,y)|Ax+By≤b,x≥0,y≥0}表示问题(1)的容许集，Πy={x∈Rn|∃y∈Rm,Ax+By≤b,x≥0,y≥0}表示S在上层决策空间中的投影.在上层决策变量x给定的情况下，S(x)表示下层问题(2)的弱有效解集.

定义1 如果(x,y)∈IR={(x,y)|(x,y)∈S,y∈S(x)}，那么(x,y)为问题(1)的可行解.

定义2 (x*,y*)∈IR为问题(1)的全局最优解，若对任意(x,y)∈IR，有:

C1x+C2y≤C1x*+C2y*.

在之后的内容中，假设以下条件成立.

(A)问题(1)的容许集S为非空紧集.

(3)

给定(x,λ)∈Πy×Ω ，ψ(x,λ) 表示问题(3)的最优解集.下面给出问题(2)的最优解集与问题(3)的最优解集之间的关系[14].

命题1[8]假设条件(A)满足，则有:S(x)=ψ(x,Ω)=∪{ψ(x,Ω)|λ∈Ω)}.

由命题1就能将问题(1)转化为如下问题，

(4)

定义5 问题(4)的全局最优解为(x*,λ*,y*)∈IR1，如果对任意(x,λ,y)∈IR1有C1x+C2y≤C1x*+C2y*.

定理1 存在ω≥0,ω∈Rp，使得:

ωTB=λTD,

(5)

ωT(Ax+By-b)=0.

(6)

是S1中的点(x,λ,y)为可行点(即(x,λ,y)∈IR1)的充分必要条件.

证明给定可行的x>0,λ>0，下层问题为，

则可以得出问题(P)的对偶问题为，

必要性 假设(x,λ,y)∈IR1，对于x>0,λ>0，y为问题(P)的最优解，由对偶原理可得，问题(D)存在最优解ω≥0，满足ωTB=λTD和ωT(b-Ax)=λTDy，就有ωTBy=λTDy=ωT(b-Ax)，即ωT(Ax+By-b)=0，必要性得证.

充分性 如果存在ω≥0，式(5)和式(6)成立，则ω是(D)的可行解.因为(x,λ,y)∈S1，则(P)的可行解是x,λ,y，由弱对偶性可得ωT(b-Ax)≥λTDy=ωTBy，综合式(6)，可知上式取等式，可以得到y和ω分别是问题(D)和(P)的最优解，那么就使得(x,λ,y)∈IR1，因此就证明了该条件的充分性.

推论1 存在ω>0，ω∈Rp，使得:

是S1中的点(x,λ,y)为可行点的必要条件.

推论2 存在ω*≥0,使得(x*,λ*,y*,ω*)为下列问题的最优解，

(7)

是(x*,λ*,y*)为问题(4)最优解的充要条件.

定理2 问题(4)的可行集IR1是容许集S1的弱拟凸子集.

证明设(x1,λ1,y1)∈S1,(x2,λ2,y2)∈S1且有α,0≤α≤1,使得(x,λ,y)=α(x1,λ1,y1)+(1-α)(x2,λ2,y2)∈IR1.通过定理1，存在ω∈Rp,ω≥0,使得：

ωTB=λTD,ωT(Ax+By-b)=αωT(Ax1+By1-b)+(1-α)ωT(Ax2+By2-b)=0.

(8)

因为(x1,λ1,y1)∈S1，(x2,λ2,y2)∈S1，则：b-Ax1-By1≥0，b-Ax2-By2≥0.

于是：

ωT(Ax1+By1-b)=0 ，ωT(Ax2+By2-b)=0.

(9)

由式(7)有ωTB≥α(λ1)TD,(ωTB)i≥α[(λ1)TD]i,故存在βi，0≤βi≤1，使得βi(ωTB)i=α[(λ1)TD]i,i=1,2,…,m.令：

则βωTB=α(λ1)TD.记βωT=α(ω1)T,则：

ω1≥0,α(ω1)TB=α(λ1)TD.

(10)

于是有：ωT-α(ω1)T=ωT-βωT=(E-β)ωT≥0.(E为单位矩阵).

令(1-α)(ω2)T=ωT-α(ω1)T,则：

ω2≥0，ωT=α(ω1)T+(1-α)(ω2)T.

(11)

由式(7)、(9)、(10)得：

α((ω1)TB-(λ1)TD)+(1-α)((ω2)TB-(λ2)TD)=0,(ω1)TB-(λ1)TD=0.

故有(ω2)TB=(λ2)TD，将式(10)带入式(8)得：

(ω1)T(Ax1+By1-b)=0 ，(ω2)T(Ax2+By2-b)=0.

通过定理1，(x1,λ1,y1)∈IR1(x2,λ2,y2)∈IR1，则IR1是弱拟凸子集.

注2 定理2可以推出S1的若干个面组成了IR1.

为了描述的方便，给出如下定义：

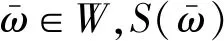
于是:

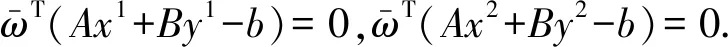
推论3IR1的极点必是S1的极点.

推论4S1的一个极点必定是最优解，如果问题(1)存在最优解.

注3 通过推论4可以得到，如果原问题最优解，并且S1的极点是有限的，那么只要检验这有限个极点是否可行，最终可以推演得出可行极点的最小值，那么就能找到问题(1)的最优解.

定理4 问题(1)的可行集IR1是连通的.

注4 通过IR1的连通性，可以知道如果我们使用搜索算法寻找问题(1)的极最优解的时候，只需要搜索IR1相邻的极点就行.

2 算法

根据以上性质，设计出了下列求解问题(1)的算法.

第1步 写出ω的基解:

注5 由定理1可以得到问题(4)的可行解的充要条件，根据该原理，就需要求出式(5)的非基础解系(ω1，ω2，…，ωp).

第2步 在给定充分大的正数α的条件下，求解如下的规划问题，

若(LPi)的可行集非空，则其最优值就是Fi；若(LPi)的可行集是空集，则Fi=-；其中i=1,2,…,p.

注6 对于每个ωi，第2步就可以得到(6)的基可行解(xl1,λl1,yl1),(xl2,λl2,yl2)，…,(xlp,λlp,ylp)，那么问题的可行极点就是该基可行解.

第3步 若max{F1,F2,…,Fm}=F(xk,λk,yk)，则(xk,λk,yk)为问题(1)的最优解.

3 数值结果

为了验证算法的可行、有效性，考虑如下半向量二层规划问题.

例1 考虑如下问题，其中x∈R3,y∈R3.

-x1-2x2-18x3-3y1-9y2-8y3)

s.t. 15x1-7x2+3x3+2y1-7y2+3y3≤200，7x1+7x2+6x3+y1+13y2+y3≤140，

2x1+2x2-x3+14y1+2y2+2y3≤240，-3x1+6x2+12x3+4y1-8y2+y3≤140，

4x1-7x2+7x3+2y1+4y2-7y3≤45，4x1+5x2+x3-7y1-6y2+y3≤800，

x1,x2,x3≥0,y1,y2,y3≥0.

将其转化为如下形式:

λ3(x1+2x2+18x3+3y1+9y2+8y3)

s.t. 15x1-7x2+3x3+2y1-7y2+3y3≤200，7x1+7x2+6x3+y1+13y2+y3≤140，

2x1+2x2-x3+14y1+2y2+2y3≤240，-3x1+6x2+12x3+4y1-8y2+y3≤140，

4x1-7x2+7x3+2y1+4y2-7y3≤45，4x1+5x2+x3-7y1-6y2+y3≤800，

x1,x2,x3≥0,y1,y2,y3≥0.

首先,得到矩阵：

运用算法求解，即:

第1步

(ω1)T=(1，0，0，0，0，0),(ω2)T=(0,1，0，0，0，0),(ω3)T=(0，0，1，0，0，0)，

(ω4)T=(0，0，0，0，1，0),(ω5)T=(0，0，0，0，0，1)，(ω6)T=(0，0，0，0，0，1).

第2步

α(ω1)TB=(2α，-7α，3α)≥(4λ1+4λ2+3λ3,7λ1+2λ2+9λ3,7λ1+4λ2+8λ3).

是不成立的，令F1=-.

α(ω2)TB=(α，13α,α)≥(4λ1+4λ2+3λ3,7λ1+2λ2+9λ3,7λ1+4λ2+8λ3)

x1+7x2+6x3+y1+13y2+y3=140，5x1-7x2+3x3+2y1-7y2+3y3≤200，

x1+7x2+6x3+y1+13y2+y3≤140，2x1+2x2-x3+14y1+2y2+2y3≤240，

-3x1+6x2+12x3+4y1-8y2+y3≤140,4x1-7x2+7x3+2y1+4y2-7y3≤45，

4x1+5x2+x3-7y1-6y2+y3≤800,x1,x2,x3≥0,y1,y2,y3≥0.

求解(LP2)问题得到(x2,λ,y2)T=(11.938 40,0.000 00,0.000 00,λ,14.177 09,2.786 012,6.035 973)T,于是F2=364.008 0.

α(ω3)TB=(14α,2α,2α)≥(4λ1+4λ2+3λ3,7λ1+2λ2+9λ3,7λ1+4λ2+8λ3)

x1+2x2-x3+14y1+2y2+2y3=240，5x1-7x2+3x3+2y1-7y2+3y3≤200，

7x1+7x2+6x3+y1+13y2+y3≤140，2x1+2x2-x3+14y1+2y2+2y3≤240，

-3x1+6x2+12x3+4y1-8y2+y3≤140，4x1-7x2+7x3+2y1+4y2-7y3≤45，

4x1+5x2+x3-7y1-6y2+y3≤800,x1,x2,x3≥0,y1,y2,y3≥0.

求解(LP3)问题得到(x3,λ,y3)T=(11.938 40,0.000 00,0.000 00,λ,14.177 09,2.786 012,6.035 973)T,于是F3=364.008 0.

α(ω4)TB=(4α，-8α,α)≥(4λ1+4λ2+3λ3,7λ1+2λ2+9λ3,7λ1+4λ2+8λ3)

是不成立的，则F4=-.

α(ω5)TB=(2α,4α,-7α)≥(4λ1+4λ2+3λ3,7λ1+2λ2+9λ3,7λ1+4λ2+8λ3)

是不成立的，则F5=-.

α(ω6)TB=(-7α，-6α,α)≥(4λ1+4λ2+3λ3,7λ1+2λ2+9λ3,7λ1+4λ2+8λ3)

是不成立的，则F6=-.

第3步 总结可以得到F3=364.008 0,最优解为

(x3,y3)T=(11.938 40,0.000 00,0.000 00;14.177 09,2.786 012,6.035 973)T.

例2 考虑如下问题，其中x∈R1,y∈R1.

s.t. 0≤x≤3，

s.t. -x-y≤-3，

-x+2y≤0，

2x+y≤12，

-3x+2y≥-4，

y≥0.

表1 算例最优解情况Tab.1 Examples of optimal solutions

例3 考虑如下问题，其中x∈R1,y∈R2.

s.t.y2≤100,x+y2≤170,x+y1+y2≤240,y1+y2≤170,-x+y1+y2≤130,-x+y2≤60,

-x-y1+y2≤20,-y1+y2≤60,x+y1-y2≤130,x≤100,x+y1≤170,y1≤100,-x+y1≤60,

-x≤-10,-x-y1≤-50，-y≤-10，x-y1≤60,x-y2≤60,x+y1-y2≤130,y1-y2≤60,

-x+y1-y2≤20,-x-y2≤-50，-x-y1-y2≤-90，-y1-y2≤-170,x-y1-y2≤20,-y2≤-10.

表1是采用所设计的搜索算法求得例2、例3得到的结果.

4 结语

运用标量化方法将所考虑的半向量二层规划问题转化为二层单层规划问题.通过分析转化后的二层单目标规划问题的可行集与容许集、容许集极点与最优解之间的关系，进而设计了求解原问题全局最优解的搜索算法.数值结果表明，所设计的极点搜索算法是可行的.