三维机织复合材料板簧式起落架结构设计及其有限元分析

王翔华， 成 玲， 张一帆， 彭海锋， 黄志文， 刘晓志

(1. 天津工业大学 纺织科学与工程学院， 天津 300387； 2. 中国直升机设计研究所， 江西 景德镇 333001)

起落架是飞机的重要部件之一，主要承担飞机起飞、降落、滑行和停放时的载荷，起到吸收飞机着陆或着舰时产生的冲击能量[1]。目前，国内外已有多种型号无人机采用了金属材料板簧式起落架(以下简称板簧)，如国产彩虹3、ASN系列无人机；美国RQ-7B幻影200等[2-3]。

随着无人机的快速发展，人们对无人机的起飞质量、巡航速度以及节能高效的更高要求，复合材料板簧应运而生。相对于航空用300M钢、4340钢以及TC18钛合金等高性能金属材料[4]，碳纤维增强复合材料不仅具有高强度，高模量，较好的抗疲劳和耐腐蚀性能，并且以其质量轻，较强的可设计性等特点，有利于降低无人机油耗，提高其续航能力，因此，复合材料已经在航空航天领域得到广泛应用[5]。近年来，国内外诸多学者对复合材料起落架研究也取得新的进展。

MURALI等[6]从起落架形状和机体结构出发，采用碳纤维复合材料制作了轻型直升机起落架，不仅满足相应设计要求，且质量减少了近25%。RASHIDI等[7]研究了单向复合材料起落架在飞机自身质量和冲击动力载荷下，相应复合层的应力分布、挠度和失效指数。杨晓等[8]依据模态叠加理论，对铺层复合材料板簧进行了落震测试，结果表明理论分析与实验测试能较好吻合。综上研究，复合材料起落架大都采用单向布或平纹布的铺层结构。铺层复合材料存在层间剪切强度较低，抗冲击性能差等缺点，较大冲击能量下容易发生失效。三维机织复合材料作为新型的结构材料，纤维在空间相互交织形成整体结构；同时三维机织复合材料在厚度方向引入了增强纤维，显著提升了材料的层间性能，能够承受更大的冲击载荷，且不易分层破坏[9]。

本文在前期研究的基础上，将板簧式起落架首先假设为等截面悬臂梁模型，运用工程力学理论进行受力分析；再采用三维机织预制体作为复合材料板簧的增强结构，结合起落架使用工况，从纤维预制体结构设计入手，同时考虑板簧的截面形状、整体构型等因素，采用有限元方法计算优化了复合材料起落架结构，设计出满足所需工况要求的板簧，以期为三维机织机织复合材料起落架制备提供理论参考。

1 板簧结构设计

1.1 设计要求

一无人机最大着陆质量WL与最大起飞质量WTo均约为550 kg，着陆沉降速度v为2 m/s；无人机前起、板簧主起与飞机重心的水平距离分别约为600、200 mm。根据实际应用需求，需设计的板簧整体高度约为400 mm，跨度为1 400 mm，机身2个安装点距离约为500 mm，同时考虑板簧与机身卡箍链接，宽度适宜范围为120～125 mm。板簧设计要求为：1)板簧产生的应力小于材料强度/1.5；2)满足安全工况下能产生足够多的挠度；3)设计结构在正常工况下不失稳。起落架基本结构如图1所示。

图1 起落架基本结构图Fig.1 Basic structure of landing gear

1.2 板簧受力及缓冲性能分析

为满足不同挠度和强度要求，在同尺寸跨度下无人机起落架轴线弯曲形状种类繁多，其中常见的有倾斜圆弧形和倾斜直线形[10]。本文主要研究截面和整体构型对复合材料板簧弹性缓冲性能的影响，不考虑机轮、机身卡箍的影响，设计时将机轮与卡箍视为钢体。本文以倾斜圆弧形进行受力分析，如图2所示。A、E点与机轮连接，B、C、D点分别与机身连接。当机轮与地面接触摩擦时，板簧与机轮连接的两端均产生垂向载荷Fy和水平载荷Fz。

图2 板簧受力简化模型Fig.2 Leaf spring force simplified model

板簧为对称双点起落架结构，着陆当量质量Wm为最大着陆质量WL的一半[11]；无人机着陆时全机最大质心过载nmax为

(1)

当无人机在地面三点水平滑跑时，板簧的垂直载荷F′y[11]为

(2)

式中，L和K分别为无人机前起、板簧主起与飞机重心的水平距离，m。

板簧在以准静态条件着陆时，在y方向弯曲变形产生静位移Δst以缓冲吸收无人机着陆产生的动能和位能。此时每个机轮给板簧的支撑力为Fy，无人机与地面撞击时必然产生冲击载荷Fd和动能；能量方程与相应关系式如下：

(3)

FZ=μWLg

(4)

(5)

式中：n为过载系数；按安全工况一般取n=2时，初步确定冲击载荷Fd=3G/2，N；FL为无人机着陆时残余升力，N，通常为无人机最大着陆质量的1/3。

由式(5)可知，增大静位移可有效降低着陆冲击过程中产生的冲击应力和冲击动载荷；然而静位移与板簧变形过程中产生的应变能Eε成正比[12]。其表达式如下：

(6)

式中：A0为板簧横截面积，m2；M(x)，FN(x)，FS(x)分别表示在点x处所受到的弯矩(N·m)，轴力(N)，剪切力(N)；E为材料弹性模量，MPa；G为材料剪切模量，MPa；I为板簧截面惯性矩，m2；k为纲量，当板簧截面为矩形时，k取1.2。

1.3 载荷计算

将设计要求代入以上公式，并由式(2)、(4)计算得出该板簧在满足上述3种要求下，机轮与地面接触后产生的垂向载荷Fy和水平载荷Fz，计算结果近似值如表1所示。摩擦因数取0.8，重力加速度取9.8 m/s2。同时，经计算，板簧若能充分吸收着陆时飞机的动能和势能，至少需产生84 mm左右的纵向位移。在后续设计中均采用该载荷数据对板簧模拟准静态加载，以优选出板簧的截面和弓形弯曲形状。

表1 板簧在不同工况下载荷情况Tab.1 Load condition of leaf spring under different working conditions

1.4 板簧截面设计

1.4.1 板簧截面设计与力学分析

基于板簧受载变形过程，可将其简化等效为等截面的悬臂梁模型[13]。梁在受外载荷弯曲变形时，横截面有剪力F和弯矩Me，剪力和弯矩能较好刻画悬臂梁模型的抗弯刚度和抗弯强度，但板簧的弯曲变形程度需通过挠度ωB进行度量，如图3所示。

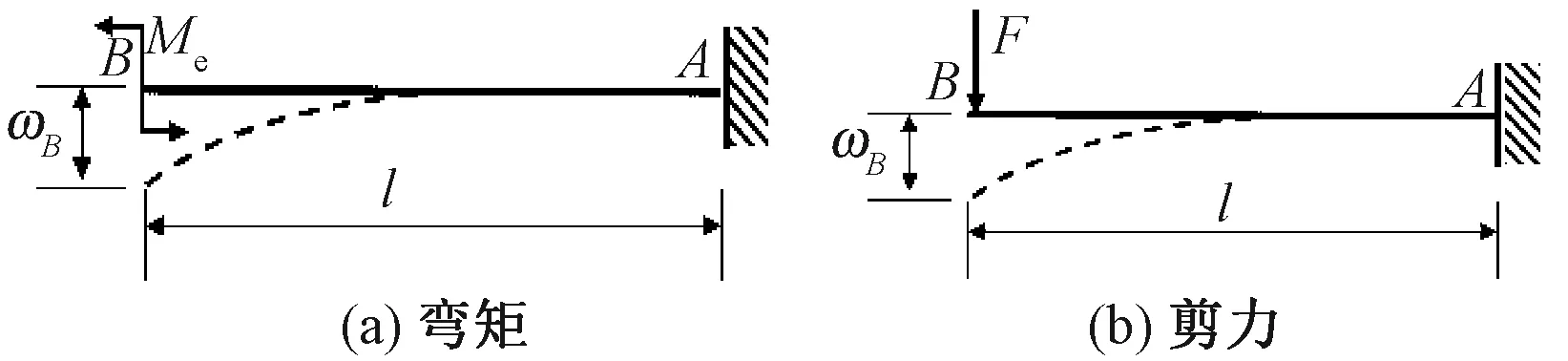
图3 悬臂梁的弯曲变形Fig.3 Bending deformation of cantilever beam. (a) Bending moment; (b) Shearing force

挠度计算公式如下：

(7)

式中：IZ为截面惯性矩，m4；l为悬臂梁长度，m。

板簧的结构设计与分析是一个反复迭代的计算过程，为满足实际工况下许用设计值的基本刚度与强度要求，以及能产生足够挠度以缓冲吸收冲击载荷，并在正常工况下保持平衡稳定，其截面厚度不宜过低或过高。对于等截面悬臂梁而言，危险截面位于距中性轴最远处ymax，即存在最大正应力σmax；则通过最大许用正应力值确定板簧厚度相应范围，公式如下：

(8)

式中：以矩形截面惯性矩为例，b、h分别为矩形截面的宽度和高度，m；WZ为抗弯截面系数，m3；M为横截面上的弯矩，N·m。则截面的厚度最小值[13]为

(9)

1.4.2 轴线形状设计

轴线设计时，考虑水平载荷与垂直载荷均会对板簧结构形成弯矩，因此，在满足相应设计要求的同时，轴线设计应尽可能使2个弯矩相互抵消。在传统板簧形状下，拟增加弧段角度，加大接触面积以减小应力等方法进行设计。由等截面直梁弯曲变形的曲率公式可知，弯矩M(t)与变形曲率ρ(t)均是随梁截面位置而变的函数，可建立梁的挠曲线方程。取距离梁原点t处截面，通过积分计算并结合相应的边界条件，可确定梁相应的挠度(ω)和转角(θ)方程[14]。

(10)

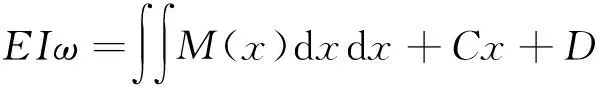
(11)

(12)

式中，C与D均为积分常数。由以上公式可知，梁不同截面位置处的挠度和转角反映了梁的弯曲变形程度，即板簧近似轴线弯曲形状。

1.4.3 截面设计

综合板簧截面受载工况和受载后正应力分布规律，以及板簧在一定挠度和强度条件下能较好满足设计要求的3个基本条件，分别设计了跑道形、矩形、梯形、斜梯形和椭圆形5种板簧截面。板簧受载后，在不同区域存在明显的应力应变差异分布[15]。由于板簧需满足相应设计要求，基于确定的截面还进行了变厚度设计，以便在弯矩较大的危险截面处，通过设计较大的截面能为板簧整体结构提供足够的强度。

2 三维机织结构设计

2.1 三维机织结构

通过载荷与有限元方法计算分析，板簧主要在长度方向上承受弯曲变形，厚度与宽度方向上承受剪切变形。结合前期不同机织结构的材料试验[16-17]，本文拟选用在长度方向含有衬经纱的 一上三下斜纹2.5维结构(如图4所示)进行编织织造，然后复合制成试样件。其中织物结构中各纱线细度分别为：接结纱24 000根单丝、衬经纱24 000根单丝、纬纱12 000根单丝；经密为(4±0.2) 根/cm，纬密为(5±0.2) 根/cm；纤维体积含量为55.42%，以便于板簧能较好承载不同方向上的载荷。

图4 斜纹2.5维机织结构Fig.4 Twill 2.5-D woven structures

2.2 组分材料参数

依据板簧结构和相应设计要求，制备复合材料板簧的组分材料分别选用了山西钢科碳材料有限责任公司的TG800-6K碳纤维(纱线线密度为249 tex)和中航复合材料有限责任公司的5284环氧树脂，其材料参数如表2所示。

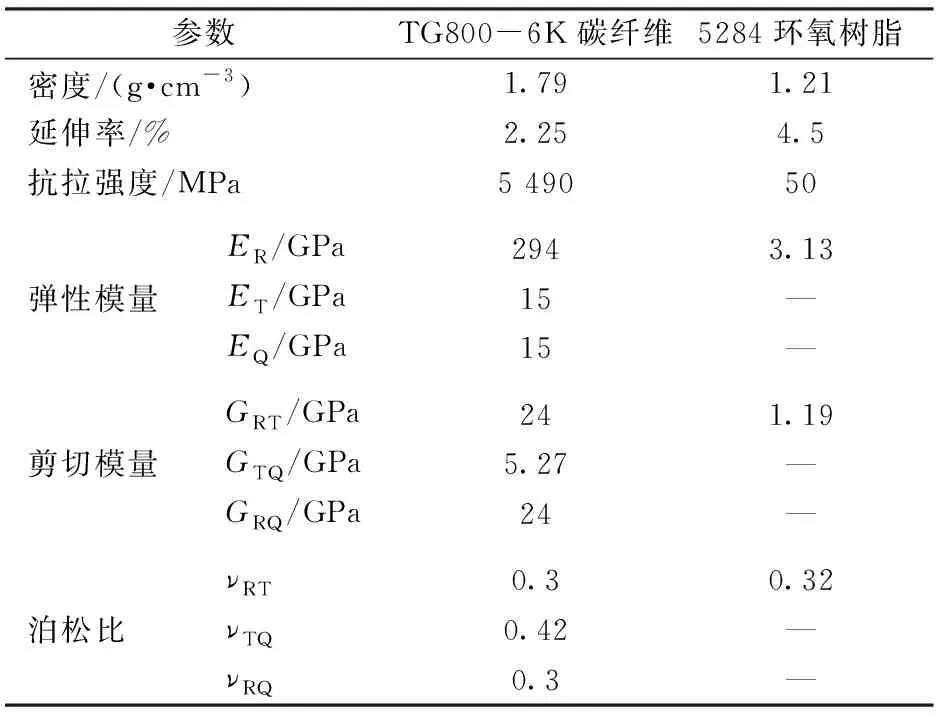
表2 三维机织复合材料组分材料性能参数Tab.2 Component material performance parameters of 3-D woven composites

注：R表示纤维束长度方向；T、Q均表示纤维束横截面方向。

2.3 三维机织复合材料工程常数理论计算

通过单向复合材料刚度平均理论可预测并求解三维机织复合材料弹性工程常数[18]。基于微观力学理论，以及增强纤维与基体在复合材料中的比例可求得单向复合材料的弹性工程常数。基体假设为各向同性材料，有Em和Vm2个常数。纤维束假设为横观各向同性材料，有Efx、Efy、Gfxy、Gfyz、νfxy5个常数。单向复合材料假设为横观各向同性材料，取其y-z平面(即垂直纤维束长度方向的横截面)为各向同性面，其中有Ey=Ez，Gxy=Gxz，νxy=νxz。则单向复合5个独立的工程弹性常数可由如下公式[19]求得：

Ex=EfxVf+EmVm

(13)

(14)

(15)

(16)

νxy=νxz=Vfνfxy+Vmνm

(17)

(18)

式中：Vf、Vm分别为增强纤维和基体的体积分数，%；ν为泊松比；x、y、z分别表示单向复合材料纵向、横向和厚度方向。

由式(13)～(18)可计算出单向复合材料弹性工程常数，代入复合材料柔度矩阵，可确定单向复合材料正轴柔度、刚度矩阵，公式如下：

(19)

式中：C表示刚度矩阵；S表示柔度矩阵。

由于三维机织结构中各纱线轴向并不都同单向复合材料那样与x轴重合；不同轴向的纱线的刚度矩阵需通过正轴刚度矩阵经坐标转换得到。

(20)

式中，[Tσ]为应力转轴矩阵。在全局坐标系下，若不同轴向纱线局部坐标系一轴与其中某一轴重合，则余下2个轴向在全局坐标系下形成夹角，从而可将应力转轴矩阵进行简化，可求解不同轴向纱线的刚度矩阵。需注意的是，对于接结经纱，其平均刚度/柔度矩阵需要考虑屈曲的圆弧段和层间直线段所占纱线长度，公式如下：

[S]=[Sij]Ldλ1+[Sij]Lcλ2

(21)

式中：[Sij]Ld，[Sij]Lc分别对应直线段和圆弧段柔度矩阵；λ1，λ2分别为直线段和圆弧段纱线占接结经纱长度比，mm。根据各个方向纤维复合材料刚度矩阵以及在三维机织复合材料中所占体积分数，代入式(22)，体积平均后可得各向异性的三维机织复合材料的总体刚度矩阵，进而得到各向异性的三维机织结构复合材料的弹性工程常数[19]。

[C]总=ks[C]s+kj[C]j+kw[C]w+

kf[C]f+km[C]m

(22)

式中，ks、kj、kw、kf、km分别为衬经纱、接结经纱、纬纱、衬纬纱和树脂在三维机织复合材料中所占的体积分数，%。

2.4 三维机织复合材料弹性工程常数确定

根据理论计算及参考ASTM标准的D2344 M—07《树脂基复合材料拉伸性能测试标准方法》、D6641 M—16《树脂基复合材料压缩性能测试标准方法》，在日本岛津(SHIM ADZW)公司生产的AG-250 KNE型万能材料实验机上进行测试；材料实验测试与理论计算弹性工程常数相应如表3所示。

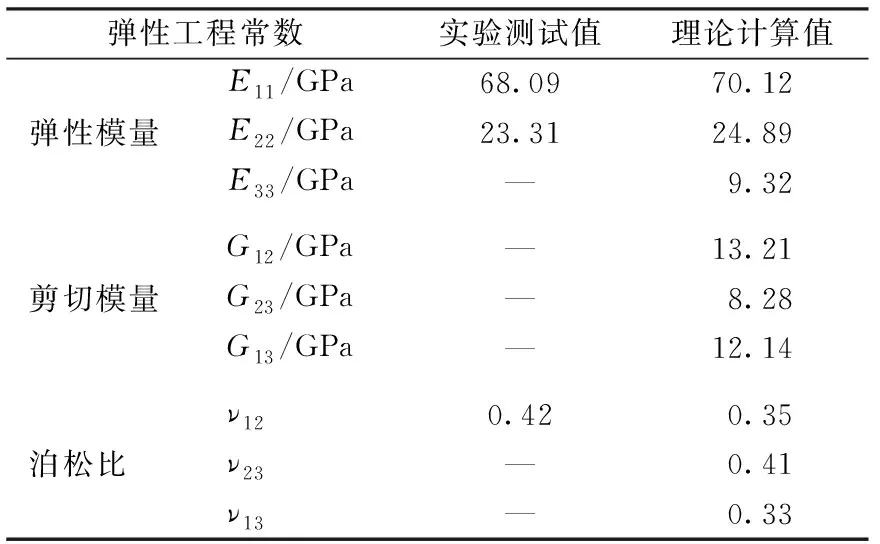
表3 三维机织复合材料弹性工程常数Tab.3 3-D woven composite elastic engineering constant

注：1代表机织经纱方向；2代表机织纬纱方向；3代表机织厚度方向。

3 有限元计算

3.1 板簧的材料属性赋予

将三维机织复合材料弹性常数赋予所设计的板簧模型，板簧在全局坐标系下局部材料属性指向如图5所示。

注：1、2、3方向分别代表局部三维机织复合材料的衬经纱、纬纱和法向纱方向。图5 三维板簧的局部材料属性方向Fig.5 Direction of local material properties of the 3-D leaf spring

3.2 边界条件与网格划分

根据复合材料板簧弯曲变形以及板簧与机身、机轮的链接方式，由于本文不考虑机轮、卡箍弹性变形，计算时将机轮与卡箍均以刚体建模以作刚化处理[20]。板簧与卡箍先后通过tie、rigid body进行边界约束，其中两边卡箍边界条件为(U1=U2=U3=UR1=UR2=0)，中间卡箍边界条件为(U1=U3=UR1=UR2=UR3=0)。其中：U1、U2、U3分别表示沿坐标轴1、2、3的平移自由度；UR1UR2、UR3分别表示沿坐标轴1、2、3的旋转自由度。根据实际工况，载荷施加位置位于机轮与地面接触点，建模时拟采用耦合约束方式将载荷等效施加于轮轴中心，实际加载工况如表1所示。为了提高计算精度，采用结构化网格单元C3D8R(8节点六面体线性减缩单元)进行网格划分。

3.3 板簧强度校核

三维机织复合材料板簧结构应力-应变分布，拟采用复合材料层合板最大应力-应变强度准则作为校核该结构是否破坏的依据，是比较保守的。单层复合材料层合板在复杂应力状态下，正轴应变不能超过材料的极限应变，否则材料将发生破坏失效[21]。最大应变准则的表达式如下：

(23)

(24)

式中：ε和γ分别表示线应变和切应变；X、Y和S分别表示纵向强度、横向强度和面内剪切强度，MPa；下标t和c分别表示拉伸和压缩；1和2分别表示复合材料纤维的纵向和横向。根据国内外各飞机设计资料，目前使用的碳纤树脂基复合材料层压板在设计载荷下的许用应变值一般为：压缩应变[εc]=-5 000；拉伸应变[εt]=6 000；剪切应变[γ]=7 600[22]。

4 结果与分析

4.1 板簧轴线弯曲形状分析

无人机板簧的轴线弯曲形状种类繁多，常见的有三角支撑形、弓式圆弧形和弓式直线形[23-24]。结合设计要求以及板簧受载后弯曲变形理论分析，在同截面下，对2种弓式弯曲形状的板簧结构进行对比分析(其中弓式圆弧形即弯曲变形部分为圆弧曲线形状；弓式直线形即弯曲变形部分为切倾斜的直线形状)，以确定板簧弯曲形状。其中均以矩形截面进行轴线弯曲形状设计分析[25]，板簧尺寸按设计要求分别取值：宽度a为120 mm，长度l为2 m，安装点距离为660 mm，厚度h为24 mm(在垂向载荷下，满足最大正应力计算的最小厚度值约为24 mm)。相应计算如表4所示。表中拉压应力、应变值普遍偏大，原因是：1)横纵向载荷在约束区域的叠加，易瞬时产生较高的应力、应变值；2)建模时，弧形区域不可避免存在尖角导致几何不连续，划分网格计算时，易产生局部应力集中，而实际中纤维复合材料板簧结构件是整体连续且光滑的。

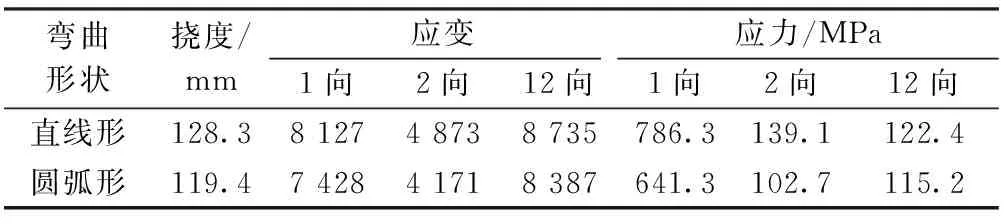
表4 同截面条件下板簧弯曲构型性能对比Tab.4 Performance comparison of leaf spring bending configuration under the same section condition

板簧冲击受载时，直线形板簧因中间卡箍区域与两端加载区域易发生负曲率弯曲变形，在产生较高挠度的同时易折剪破坏，为满足安全工况，此结构对材料强度要求较高。圆弧形板簧构型在受载过程中一直保持正曲率弯曲变形，能有效缓冲飞机着陆能量的同时不易失稳破坏，且满足强度要求，是满足1.1节设计要求的理想弯曲构型。

4.2 等截面板簧设计分析

通过式(7)～(12)计算板簧截面厚度会显著影响板簧弯曲挠度。截面厚度增加，截面惯性矩增加，挠度则减小，所以在等截面分析中，在各截面面积相等的条件下，厚度也需相同。根据计算厚度h取值为24 mm。在有限元分析过程中，材料参数(理论计算值)、边界条件以及网格单元类型均保持不变，以优选出三维机织复合材料板簧截面；不同截面板簧变形的应力云图如图6所示。通过分析发现，椭圆形截面的板簧受载后整体结构发生18.2°角度横向偏转，说明受载后椭圆形截面容易失稳，且椭圆形截面产生较低挠度不能有效缓冲载荷。由图6可知：跑道形截面与斜梯形截面能较好克服剪切变形；梯形截面的板簧结构能较好地优化截面内正应力分布以及能产生足够挠度以缓冲吸能，但实际中设计织造工艺较为复杂，编织效率较低；矩形截面板簧稳定性较好，织造效率高，在固有载荷下满足挠度要求的同时，1方向的应力值最小，能更好地满足材料强度要求，是板簧结构理想的截面形式。

4.3 变截面板簧设计分析

在等截面板簧分析中，不同截面形状的板簧结构在相同厚度下均满足挠度要求；但在1方向应变值和应力值均已超过材料许用应变值或许用应力值。由图6可知，沿着板簧长度方向，板簧在不同区域出现不同的应力、应变值。其中最大的应力均主要集中于卡箍约束区域，说明转动卡箍制约了板簧因受载荷而产生的弯曲变形，致使2种载荷在此处叠加； 所以将研究重点放在对称增加板簧截面厚度设计分析上，使得板簧在载荷条件下，挠度、应力与应变均能满足设计要求。本节在板簧宽度a为120 mm，厚度h为24 mm的基础上，改变局部增厚的长度、厚度值并对2个因素结合理论和设定范围进行对比分析，以优选出增厚长度、厚度值。

4.3.1 局部增厚的长度值分析

4.1与4.2节分析发现，板簧主要在1方向(即板簧长度方向)承受主要的拉压应力应变，同时在12方向(即面内方向)与13方向(即厚度方向)承受较大剪切应变。在优选长度值时，综合理论计算，拟增厚值h′设定为36 mm；增厚长度l′分别设定为700、720、740、760、780 mm。相应计算结果如图7所示。

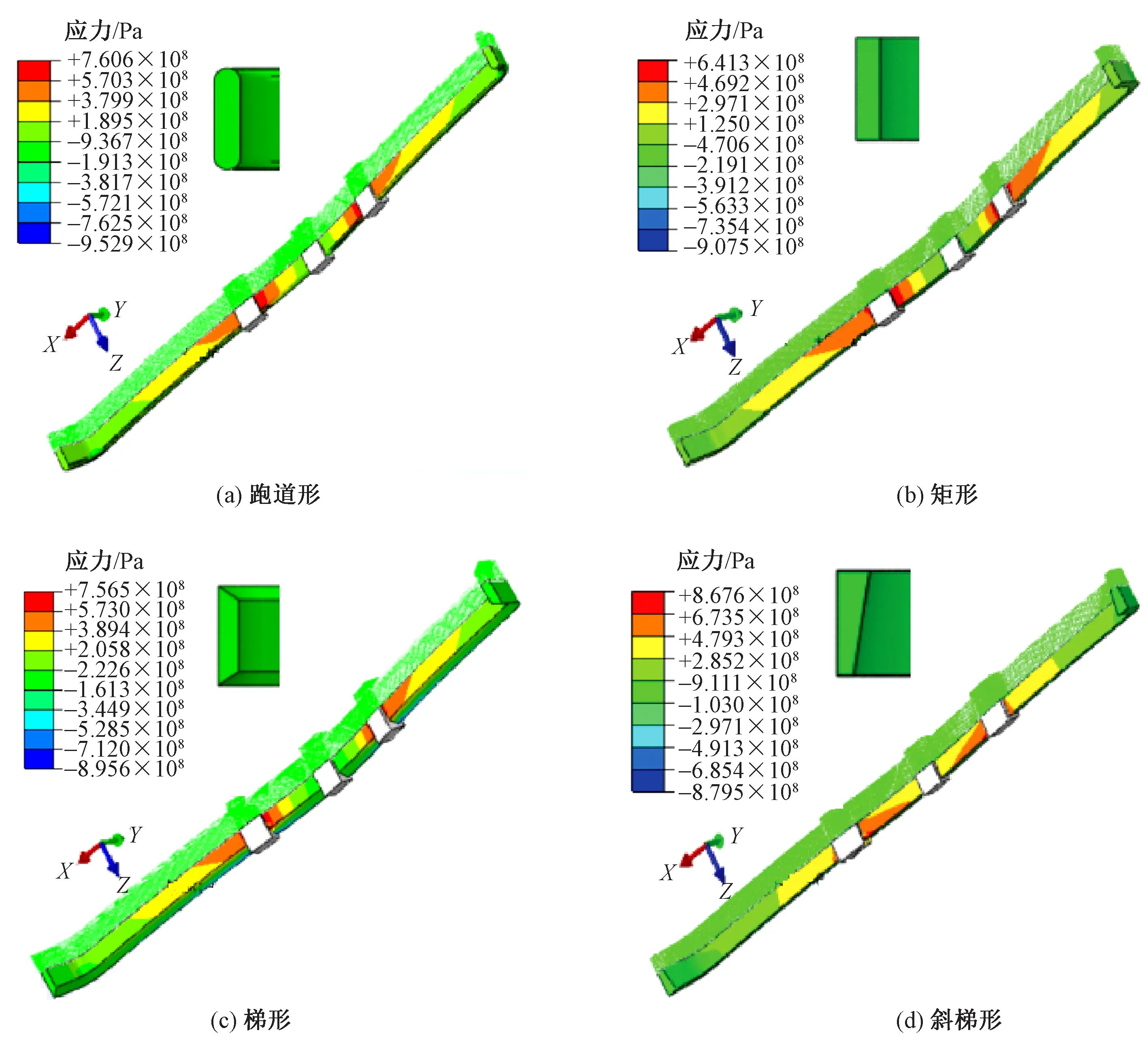
图6 不同截面的三维板簧变形应力云图Fig.6 3-D leaf spring deformation stress cloud diagram with different cross sections.(a)Racetrack shape;(b)Rectangle;(c)Trapezoid;(d)Oblique trapezoid

图7 增厚长度情况下板簧力学性能曲线Fig.7 Mechanical performance curve of leaf spring under thickened length. (a)Thickened length-deflection/stress curve； (b)Thickened length-deflection/strain curve

从图7看出，在增厚度至一定条件下，板簧受载后产生的挠度、应力与应变值随增厚长度的增加而明显下降；同时在板簧长度(即纤维衬经纱方向)以及面内、厚度等方向，分别产生了较大的应力σ11、线应变ε11和切应变γ12、γ13值，表明这些方向为板簧承受弯曲变形的主要方向。在板簧增厚长度为760 mm时，板簧挠度不仅能满足设计要求，应力、应变值也在许用值范围内。这一现象可从另一方面说明，板簧厚度值增大，其截面惯性矩较高，板簧不易弯曲，挠度较小。

4.3.2 局部增厚的厚度值分析

基于优选出的增厚长度，通过改变板簧局部厚度对板簧进行对比分析，以优选板簧增厚厚度。结合织造工艺与设计要求，依次设定板簧增厚厚度值为28、30、32、34、36、38 mm，计算结果变化曲线如图8所示，卡箍与板簧接触变形如图9所示，板簧变形云图如图10所示。需说明的是，板簧整体变形与图6基本一致，均为正曲率变形。

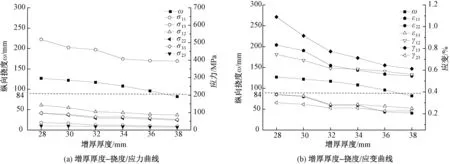
图8 增厚厚度情况下板簧力学性能曲线Fig.8 Mechanical properties of leaf spring under thickened thickness. (a)Thickness-deflection/stress curve;(b) Thickness-deflection/strain curve

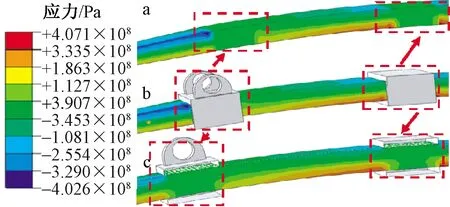
图9 板簧局部区域应力云图Fig.9 Local area stress cloud diagram of leaf spring

由图8可知，随着厚度的增加，应力值逐渐降低且过渡区域的应力集中区域逐渐消失，而中间卡箍区域的应力值逐渐减小；表明板簧局部厚度的增加，使得板簧由局部承载到整体承载，发挥了板簧整体结构有效缓冲吸能的作用，从而延长板簧的使用时效。需注意的是，随着增厚厚度值继续增加，挠度明显减小。然而挠度过小，不足以缓冲吸收着陆冲击产生的能量，所以应力与应变值在小于许用应力与应变值条件下，挠度应越高则越有意义。

从图9可明显看出：弹性板簧在紧靠转动卡箍区域，上端出现最大压缩应力476.2 MPa；紧靠定位卡箍区域，下端出现最大拉伸应力407.1 MPa；而在完全接触的中间区域，最大应力均低于200 MPa，表明弹性板簧与卡箍完全接触区域的应力较小。最大变形发生于即将接触区域的上下两端，进一步表明了板簧变形受卡箍的制约。从图10(e)可看到，优选厚度值h′为36 mm，其受载后产生1方向应力与应变值分别为：367.2 MPa，0.563%。

结合图8、9，由图10可看出，沿着板簧长度方向，板簧产生的最大应力区域主要集中在由薄变厚的过渡区域和刚性卡箍约束狭小的区域。说明板簧受横向和纵向受载过程中，转动式卡箍在一定程度上制约了板簧转动的幅度，易瞬时产生较高的弯曲拉伸变形和剪切变形；而由薄变厚过渡的区域，因载荷在此处叠加，以及几何建模结构的不连续是产生应力、应变集中的主要原因。

4.4 不同材料板簧质量对比

通过优选出的板簧截面形状、弓式弯曲形状以及变截面相应的长度值和厚度值，进行板簧结构件设计，并与同类型板簧起落架常用的材料性能进行对比[26]。分析发现，基于航空用4340钢制成的同类型的板簧结构件，三维机织复合材料板簧结构件质量减少约30%，说明三维机织复合材料板簧起落架可以实现质量减少的目的。

5 结 论

1)本文在给定设计要求下，通过对板簧进行受力分析和理论计算，结合受载工况和受载后正应力分布规律，计算出了板簧所承载荷，设计了5种板簧截面。其中矩形截面在设计载荷下满足挠度要求，其应力与应变值最小，能更好地满足材料强度要求，且矩形截面易织造成型。

2)结合材料实验与理论计算，确定了三维板簧有限元计算所需的材料工程常数。根据强度校核以及复合材料层合板许用应变值，确定了板簧轴线弯曲形状、板簧截面形状以及变截面板簧的增厚长度值与增厚厚度值。

3)弓式圆弧形、矩形截面的板簧在满足挠度的同时，应变低于材料许用应变值；在板簧宽度a为120 mm，厚度h为24 mm基础上，随着局部增厚长度或局部增厚厚度的增加，板簧所产生的挠度、应力与应变均显著降低。其中增厚长度为760 mm，增厚厚度值为36 mm时，其挠度为96.7 mm，应力、应变分别为367.2 MPa，0.563%，满足设计要求。

4)根据优选出的板簧设计参数，基于相同类型的航空用4340钢制成板簧结构件，三维机织复合材料板簧质量减少约30%。本文设计研究结果对后期继续结构优化研究具有一定的指导意义，但在后期研究中需进一步考虑有限元计算与实验测试的吻合程度。