非线性矩阵方程X+A*X-1A-B*X-1B=I的Hermitian 正定解

邢智勇

(邵阳学院 理学院,湖南 邵阳,422000)

矩阵方程X±A*X-1A=I在电子网络[1]、梯形网格[2]、动态规划[3-4]、统计学[5-6]、排队论[7]、高斯反过程[8]、随机渗入[9]等领域有着广泛的应用。许多学者对它们展开了系统而深入的研究。文献[10]证明了矩阵X+A*X-1A=I存在Hermitian正定解的充要条件是矩阵A的数值域包含在复平面中半径为1/2的闭圆盘中(即ω(A)≤1/2),这里矩阵A是可逆的。文献[11]给出了矩阵方程X+ATX-1A=I存在 Hermitian 正定解的一些充分条件和必要条件。文献[12]证明了矩阵方程X=Q+NX-1N*同时存在最大解和最小解。随后许多学者提出了计算这些矩阵方程 Hermitian 正定解的一些算法[13-14]。文献[15]给出了矩阵方程X±A*X-1A=IHermitian，正定解界的估计。最近有许多学者研究了上述两个矩阵方程的一些推广形式[16-18]。然而，迄今为止鲜有关于矩阵方程

X+A*X-1A-B*X-1B=I

(1)

Hermitian 正定解的研究。 若取A=0,则矩阵方程(1)转化为X-B*X-1B=I。若取B=0,则矩阵方程(1)转化为X+A*X-1A=I。因此，矩阵方程(1)可视为上述两类矩阵方程的综合与推广。

本文研究了矩阵方程(1)Hermitian 正定解的存在性，获得了矩阵方程(1)存在 Hermitian 正定解的一些充分条件和必要条件。

1 矩阵方程(1)存在Hermitian正定解的必要条件

为了便于获得矩阵方程(1)存在Hermitian正定解的必要条件,先证明如下引理。

引理1 若X为n阶Hermitian正定矩阵,则 trX·trX-1≥n2,这里trX为矩阵X的迹。

证明 设λ1,λ2,…,λn为Hermitian正定矩阵X的全体特征值,则1/λ1,1/λ2,…,1/λn为矩阵X-1的全体特征值。于是

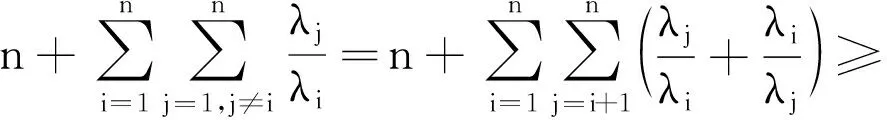
运用引理1,可以获得方程(1)存在Hermitian正定解的必要条件。

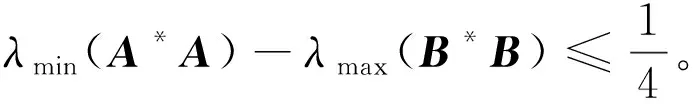
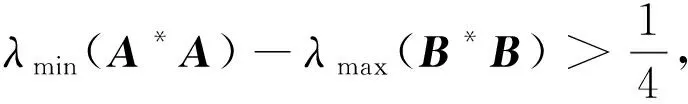
trIn=trX+tr(A*X-1A)-tr(B*X-1B)≥

trX+[λmin(A*A)-λmax(B*B)]trX-1≥

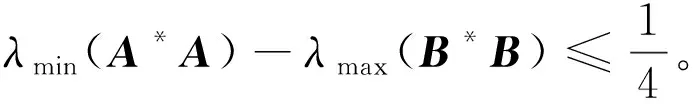
2 矩阵方程(1)存在Hermitian正定解的充分条件

为了便于理论分析,定义如下2个映射:

F(X)=I-A*X-1A+B*X-1B
G(X)=A(I-X+B*X-1B)-1A*。

定理3 若矩阵方程X+A*X-1A=I存在Hermitian正定解,则矩阵方程(1)存在Hermitian 正定解。

证明 设X1为矩阵方程X+A*X-1A=I的1个Hermitian正定解。记

Ω={X:X1≤X≤I+B*X1-1B}。

显然,Ω是一个有界的闭凸集且F(X) 在Ω上连续。对任意X∈Ω有

F(X)≥I-A*X-1A≥I-A*X1-1A=X1
F(X)≤I+B*X-1B≤I+B*X1-1B

因此F(Ω)⊆Ω。由Brouwer 不动点定理知F(X) 在Ω上存在不动点,此不动点即为矩阵方程(1)的Hermitian正定解。

定理4 若ω(A)≤1/2,则矩阵方程(1)存在Hermitian正定解。

证明 文献[10]证明了当ω(A)≤1/2时矩阵X+A*X-1A=I存在Hermitian正定解。由定理3知此时矩阵方程(1)存在Hermitian正定解。

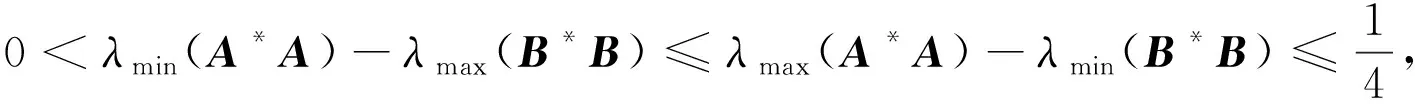
证明 考虑如下标量方程:

λ2-λ+λmax(A*A)-λmin(B*B)=0

(2)

λ2-λ+λmin(A*A)-λmax(B*B)=0

(3)

因为λmax(A*A)-λmin(B*B)≤1/4, 方程(2)有2个实根：

同理，方程(3)有2个实根：

因λmin(A*A)-λmax(B*B)>0,从而β2≥β1≥α2≥α1>0。

记Ω′=[α1I,α2I], 则Ω′为有界的闭凸集且G为Ω′上的连续映射。由定义

于是

从而

A*(α1I)-1A≥I-α1I+B*(α1I)-1B
(α1I)-1≥A-*(I-α1I+B*(α1I)-1B)A-1
α1I≤A(I-α1I+B*(α1I)-1B)-1A*

因此，α1I≤G(α1I)。 类似可得α2I≥G(α2I)。由映射G在Ω′上单调递增可得,对 ∀X∈Ω′，有

α1I≤G(α1I)≤G(X)≤G(α2I)≤α2I,

因此G(Ω′)⊆Ω′,由Brouwer 不动点定理知G(X) 在Ω′上存在不动点,此不动点即为矩阵方程(1)的Hermitian正定解。

3 数值例子

本小节将给出一些数值例子验证本文结论的正确性。

例1 令

矩阵A的全体特征值为{1.417 1,5.251 3,8.331 6}, 因此，A为Hermitian正定矩阵。经计算可得 trA·trA-1=15.241 9>32=9。

例2 考虑矩阵方程(1),其中,

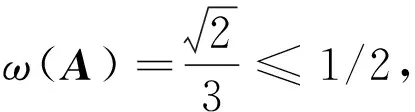
均为矩阵方程(1)的Hermitian正定解。

例3 考虑矩阵方程(1),其中，

由定理5可得矩阵方程(1)存在Hermitian正定解。实际上,直接计算可得

均为矩阵方程(1)的Hermitian正定解。