核动力装置运行数据的特征提取方法研究

彭彬森，夏 虹，朱少民，彭敏俊，刘永阔，马心童

(哈尔滨工程大学 核安全与仿真技术国防重点学科实验室，黑龙江 哈尔滨 150001)

随着中国能源供给侧进行深入的改革，核能在能源结构中的占比越来越高。与此同时，大众对核设施安全性的关注也越来越高，尤其是在日本福岛核事故后，如何保障核动力装置的安全性已成为影响核能发展的重要因素[1-2]。核动力装置是一个非常复杂的动态时变系统，主要是因其运行条件复杂可变[3]。一旦发生异常，操纵员需对异常情况进行分析，找出异常的原因，并及时采取措施降低事故的影响，确保核动力装置的安全运行，否则将造成巨大的损失和影响，因此状态监测系统在保障核动力装置安全性方面扮演着重要的角色。核动力装置在运行过程中，监测系统需对许多参数进行监控，主要有温度、压力、水位等热工参数以及机械振动参数，同时同一过程中的不同变量间往往互相关联，这些运行数据主要有以下特点[4]：1) 来源多重性，数据源是多种多样的，且大小不一的系统并存；2) 空间分布性，数据源在空间中的分布各不相同；3) 时间多尺度性，数据时间跨度大、差别很大；4) 实时交互性，各系统及设备的运行数据等可实时反映核动力装置的运行状态；5) 数据的价值密度低，多数数据均是正常数据，故障数据少。大量复杂的过程变量给操纵员对系统状态的判断带来了困难。因此需将较多的过程变量压缩为少数独立的变量，智能特征提取方法自动编码器是一种高维数据分析的有效手段，通过分析得到的低维特征变量很好地保留了原始数据的特征信息，摒弃了冗余信息，不仅降低了计算量，同时也提高了数据的识别精度[5]。因此本文采用稀疏自动编码器(SAE)对核动力装置产生的高维信号进行特征提取，并对提取后的数据进行异常识别。

1 SAE数据特征提取

1.1 自动编码器(AE)

AE是一种人工神经网络，采用无监督的学习方式从原始数据中提取特征信息[6]。AE作为构建深度神经网络的基本结构，其特征之一是输入节点的值等于输出节点的值。另一个特征是隐藏层中的神经元数量通常小于输出层的，因此它具有通过非线性变换将输入特性转换到少量隐藏层神经元中的优点。使用自动编码算法，不仅可减少数据维数，省去了手动提取特征的麻烦，同时还能降低计算复杂度，减少计算资源的占用[7]。

AE由编码器和解码器组成，其结构如图1所示。输入数据首先通过编码器映射到低维空间，然后再通过解码器将数据还原，还原的数据与原始数据的误差越小，说明AE的效果越好。AE可从未标记的数据中提取特征值，并提供原始特征的表示。解码器用于对原始输入进行重构，原始输入可视为编码器的逆输入[8]。

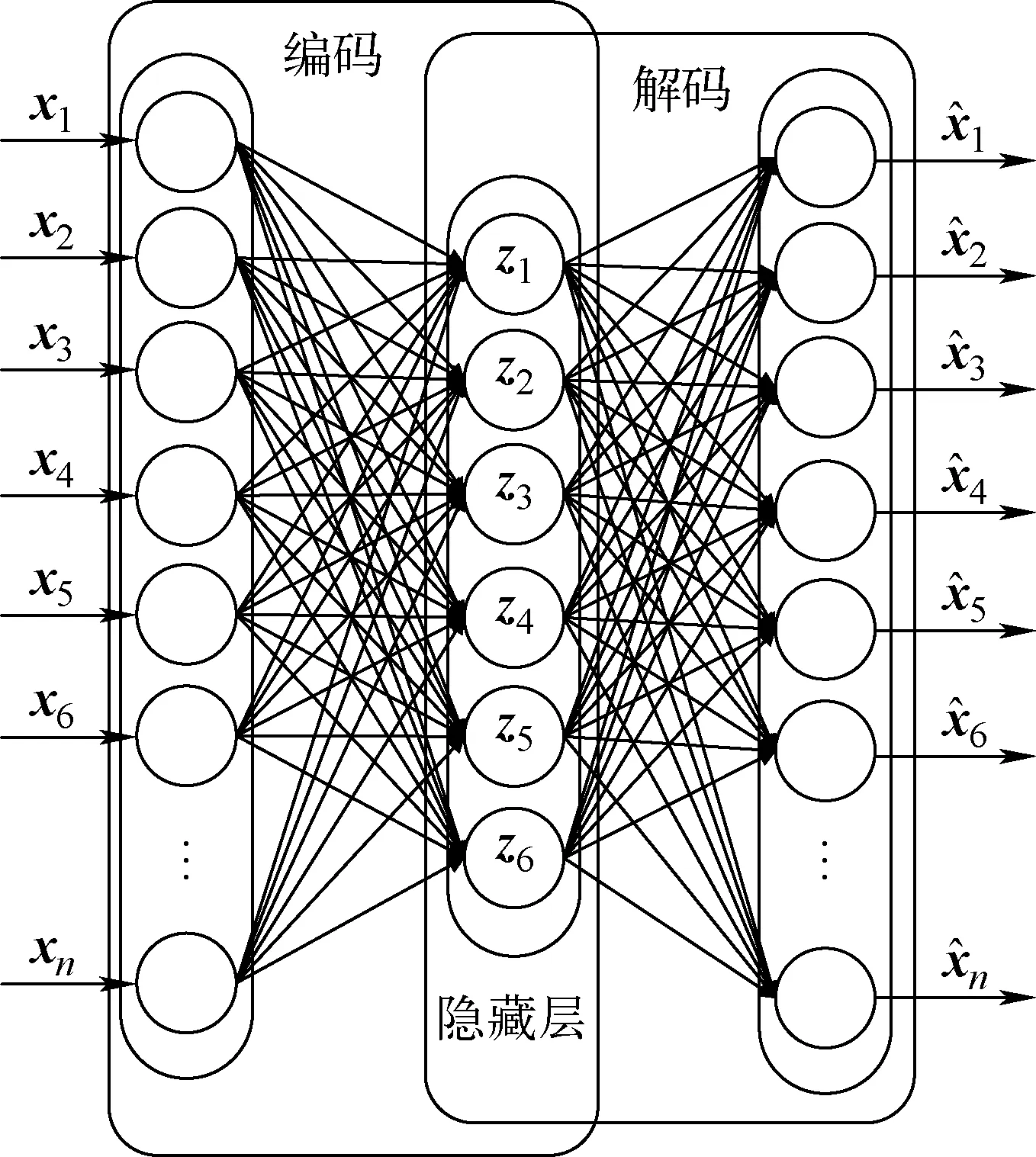
图1 AE的简化结构Fig.1 Simplified structure of AE

如果输入到AE的是矢量x，则编码器可将矢量x映射到另一个矢量z，如下所示：

z=h(1)(w(1)x+b(1))

(1)

(2)

式中：上标(2)表示第2层；h(2):h(z)=z，为解码器的线性传递函数(purelin函数)。

为优化AE的训练效果，引入损失函数作为训练的目标函数，损失函数包括重构误差项和L2正则化项，如式(3)所示。

JAE(w,b)=err+λΩweights

(3)

式中：err为输出的重构值与输入的实际值之间的均方误差，其表达式如式(4)所示；Ωweights为L2正则化项，用于减少w(1)，增加z(1)，从而防止模型过度拟合；λ为式(5)中给出的L2正则化项的系数。

(4)

(5)

式中：L为隐藏层的层数；N为训练样本的数据个数；K为训练数据中包含的参数个数。

1.2 SAE

大量研究表明，当生物视觉系统的主要处理区域对信号进行分析时，仅有少数神经元处于激活状态，而大多数神经元处于抑制状态，并且获得的稀疏表达通常较其他表达更有效[8]。SAE是通过在AE的基础上引入稀疏限制而建立的，其结构如图2所示[9]。如果激活函数为sigmoid函数，当隐藏层神经元的值接近1时，该神经元被激活；当隐藏层神经元的值接近0时，该神经元被抑制。

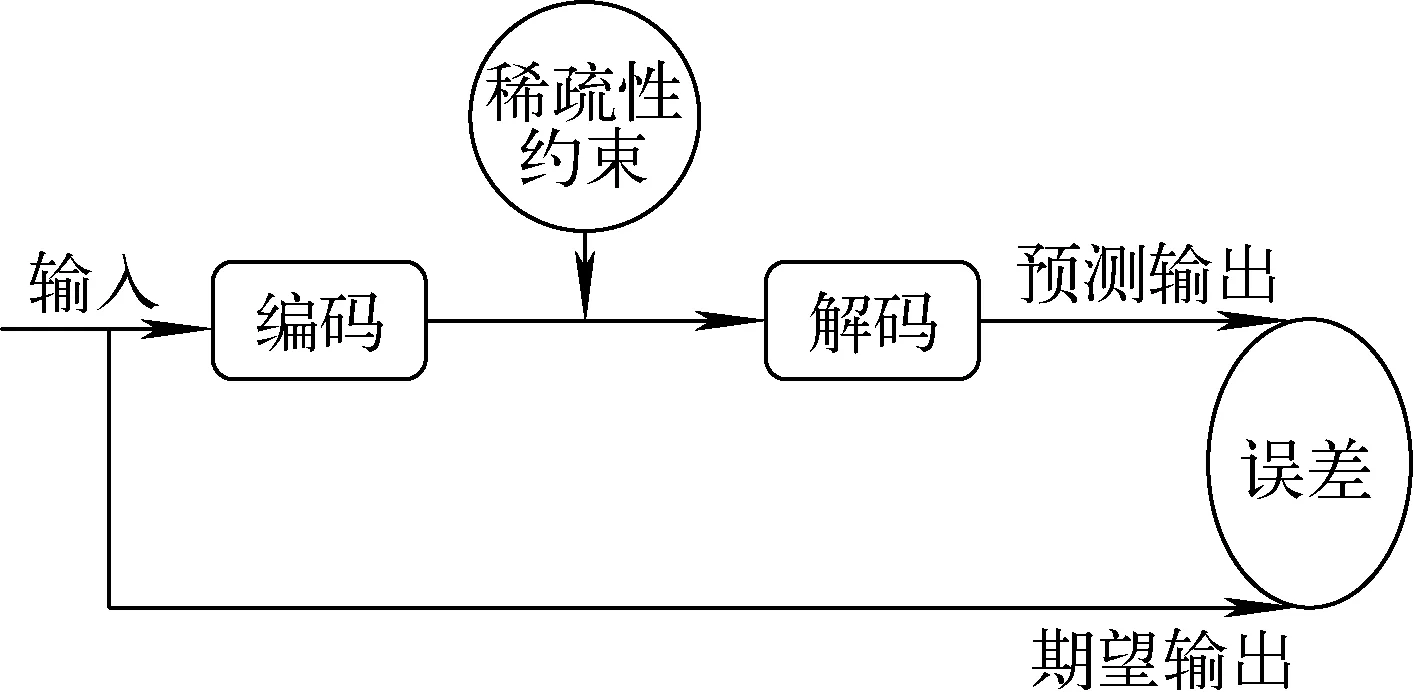
图2 SAE结构简图Fig.2 Structure schematic of SAE

(6)

式中：n为训练样本的总数；xj为第j个训练样本。

通过在式(3)中添加稀疏性正则化项，可得SAE损失函数为：

JSAE(w,b)=JAE(w,b)+βΩsparsity

(7)

(8)

1.3 训练SAE

在SAE的训练中，通常利用反向传播(BP)算法来优化神经网络的参数，当代价函数达到误差限值或迭代次数达到最大值时，停止训练。其中权重和偏差在训练过程中的迭代更新如下[12]：

(9)

(10)

1.4 核动力装置数据特征提取

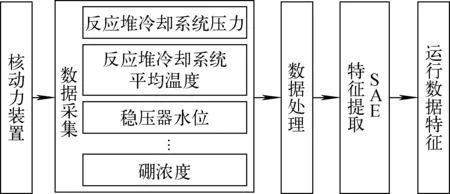
图3 核动力装置运行数据特征提取流程图Fig.3 Flow chart of feature extraction for nuclear power plant operation data

根据核动力装置的特点，设计如图3所示的特征提取流程图，主要包括3个阶段：数据采集阶段、数据处理阶段和特征提取阶段。首先在数据采集阶段获取不同设备的主要参数值，然后在数据处理阶段对数据进行必要的预处理使数据符合要求，最后在特征提取阶段将原始数据压缩至低维特征空间，从而得到相应的特征值。

2 仿真测试与结果

为验证该方法的可行性，将其应用到核动力装置的状态监测中，状态监测方法为孤立森林方法[13]。为此用核动力装置仿真软件PCTRAN模拟了9种不同的运行工况(正常工况和异常工况)，并获得了相应的时间序列参数[14-15]。表1列出了工况类型与样本数量。训练数据样本由4 000个数据组成，共包含64个参数，其中异常数据有1 000个(故障程度范围为5%～50%，破口事故故障程度为破口面积与总截面积比值，甩负荷事故故障程度为负荷与满功率比值)，100%满功率下的正常数据有1 000个，90%满功率下的正常数据有1 000个，80%满功率下的正常数据有1 000个。为验证该方法在单一正常工况下和多种正常工况下状态监测的有效性，考虑到实际情况下正常数据较异常数据多，按正常数据与异常数据的比例为9∶2从总样本集中抽取1 100个数据组成训练样本。测试过程中共抽取了3组训练样本，第1组包含200个异常数据，900个100%满功率正常数据；第2组包含200个异常数据，450个100%满功率正常数据，450个90%满功率正常数据；第3组包含200个异常数据，300

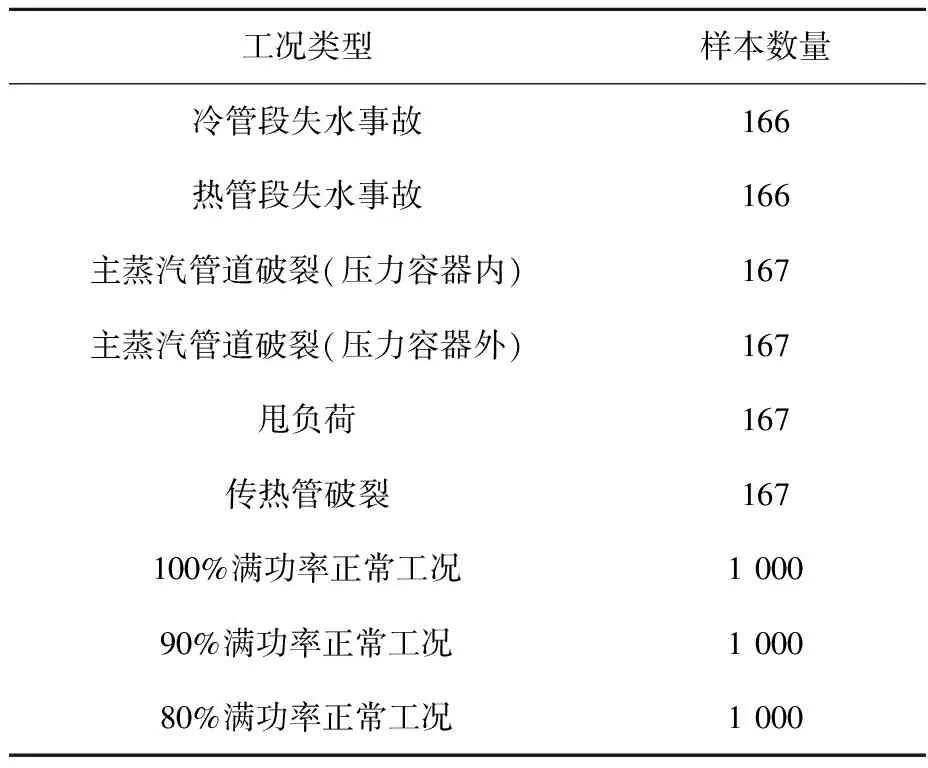
表1 工况类型与样本数量Table 1 Condition type and sample count

个100%满功率正常数据，300个90%满功率正常数据，300个80%满功率正常数据。

为体现SAE的优势，同时用不含稀疏项的AE作为对照，对相同的数据进行测试，相关参数设置列于表2。

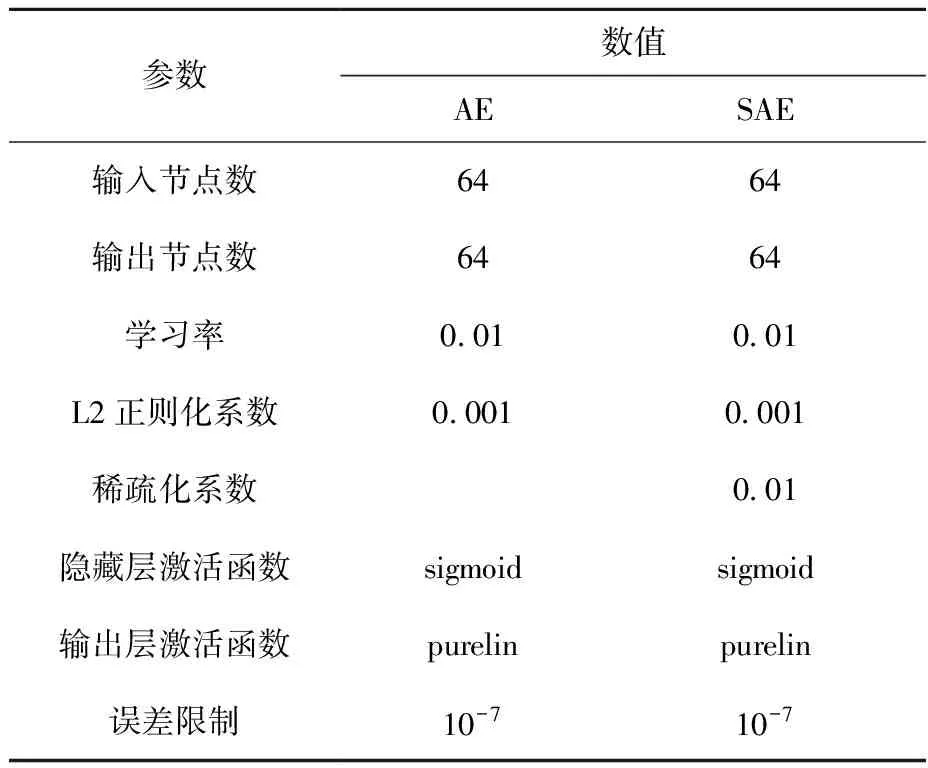
表2 参数设置Table 2 Parameter setting

2.1 数据预处理

为更有效地提取特征和训练状态监测模型，需对数据进行归一化处理，通过归一化既能消除量纲的影响同时又能保留数据的原始特征信息，本文采用极差归一化法对原始数据进行预处理，其表达式为：

i=1,2,…,n，xi(t)∈[0,1]

(11)

式中，ximax(t)和ximin(t)分别为xi(t)的最大值和最小值。经归一化后，所有参数值均被限制在[0,1]范围内，然后就能被用来训练SAE模型和状态监测模型。

2.2 评价指标

通过设置SAE隐藏层神经元的数量，可获得与隐藏层神经元数量对应的提取特征的维数。为评价提取特征的质量，使用SAE训练迭代收敛到相同误差精度的迭代次数和受试者工作特性(ROC)曲线下的面积(AUC)作为评估标准。在优先保证AUC足够大的情况下，迭代次数越少，说明所提取特征的质量越好。

2.3 特征提取结果

1) 案例1

该案例所用数据样本包含200个异常数据，900个100%满功率正常数据，共1 100个数据。图4为案例1 AUC和训练迭代次数与特征维度的关系。从图4a可看出，AE的AUC在不同特征维度下的取值波动较大，且最大精度不超过96%，而SAE的AUC在不同特征维度下的取值比较稳定，并能保持较高精度。从图4b可看出，AE的收敛次数少，SAE的收敛次数较多，且随特征维度的增加而明显增加，结合图4a的AUC，可认为AE易提前陷入局部最小值，而SAE尽管训练收敛次数偏多，但更易找到全局最优解。通过观察图4a中SAE的AUC与特征维度关系曲线可发现，当特征维度取1时，AUC下降较明显；当特征维度大于6时，AUC呈下降趋势。当特征维度为3、4、5或6时，AUC能取到最大值1，这说明状态监测模型此时能有最大识别率。考虑到迭代次数应越小越好，因此当特征维度取3时，可认为是最佳情况。

图5为特征维度分别为1、2和3时的可视化结果，可视化结果由等高线图和散点图组成。其中蓝色区域为正常状态区域，当异常分数接近于0时，蓝色程度加深，这意味着该区域的数据为正常数据的可能性更高。黄色区域为异常区域，当异常分数接近于1时，黄色程度加深，这意味着该区域的数据为异常数据的可能性更高。如图5a所示，为使可视化效果更好，当提取特征维度取1时，用极坐标图对结果进行展示，半径为特征参数的取值。图5b、c的坐标轴参数为相应特征维度下的特征参数。

特征提取结果显示经特征提取后，正常数据都集中在原点区域，异常数据以离散形式分布在正常数据周围。通过局部放大图可发现，当特征维度取1和2时，在正常数据周围有一部分数据被错误分类，当特征维度取3时，无数据被误判。因此可认为将数据压缩至3维特征空间，可作为最佳维度去训练状态监测模型。

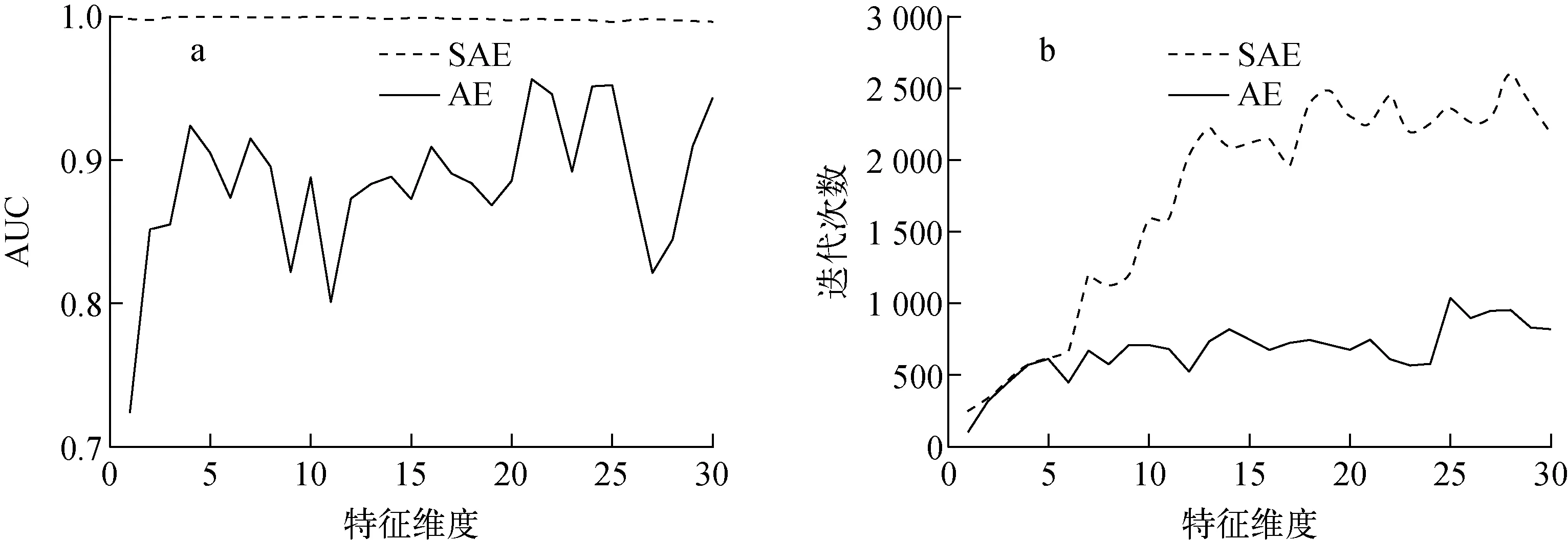
图4 案例1 AUC和训练迭代次数与特征维度的关系Fig.4 AUC and training iteration under different feature dimensions for case 1

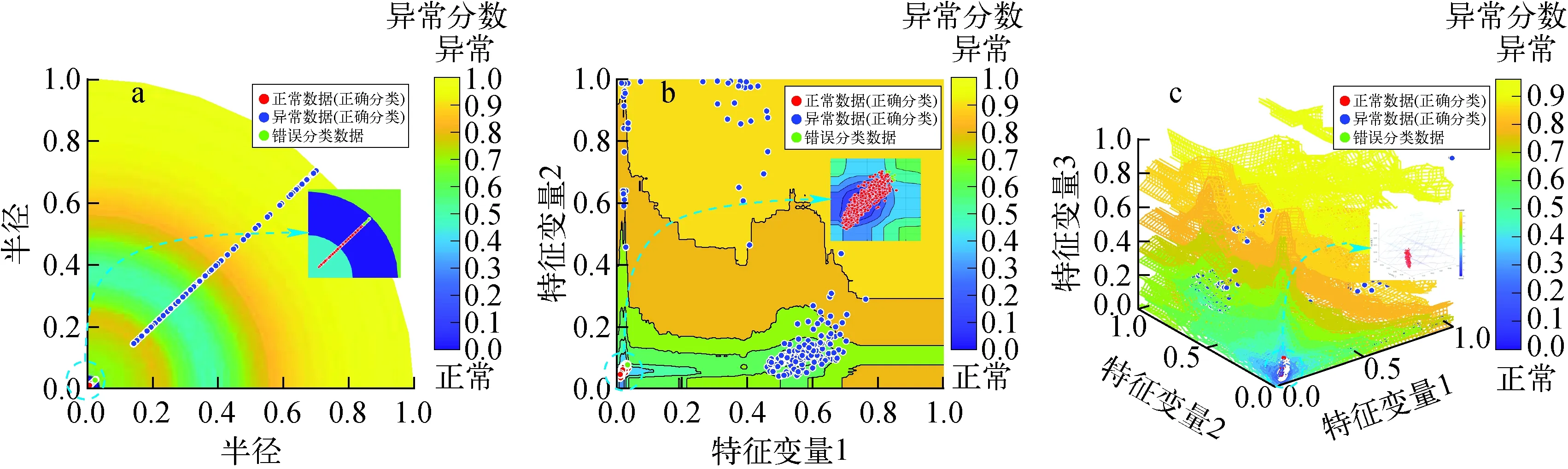
图5 案例1当特征维度为1(a)、2(b)、3(c)时的可视化结果Fig.5 Visualization results for feature dimensions taken as 1(a), 2(b) and 3(c) for case 1

2) 案例2

该案例所用数据样本包含200个异常数据，450个100%满功率正常数据，450个90%满功率正常数据，共1 100个数据。图6为案例2 AUC和训练迭代次数与特征维度的关系。从图6a可看出，该结果与案例1类似，AE的AUC在不同特征维度下的取值波动较大，而SAE的AUC在不同特征维度下的取值较稳定，并能保持较高精度。从图6b可看出，AE的收敛次数少，SAE的收敛次数较多，且随特征维度的增加而明显增加，结合图6a的AUC，可认为AE易提前陷入局部最小值，而SAE尽管训练收敛次数偏多，但更易找到全局最优解。通过观察SAE的训练迭代次数与特征维度关系曲线可看出，提取特征维度越小，训练迭代的次数越少，当提取特征维度小于16时，迭代次数有一明显的下降趋势。通过观察SAE的AUC与提取特征维度关系曲线可发现，当特征维度取1时，AUC下降较明显；当特征维度大于7时，AUC呈下降趋势。当特征维度为4时，AUC能取到最大值0.994 9，这说明状态监测模型此时具有最大识别率，同时又能取得较低的迭代次数，因此当特征维度取4时，可认为是最佳的情况。

图7为特征维度分别为1、2和3时的可视化结果。当特征维度取1时，在异常分数接近于0的区域，存在明显的误判，这说明1维特征不能反映数据的本质特征。图7b、c可发现，正常数据主要集中在两个区域，这说明了数据中包含两类正常数据，异常数据主要分布在正常数据周围。通过局部放大图可发现，在正常数据周围存在一些误判。

3) 案例3

该案例所用数据样本包含200个异常数据，300个100%满功率正常数据，300个90%满功率正常数据，300个80%满功率正常数据，共1 100个数据。图8为案例3 AUC和训练迭代次数与特征维度的关系。从图8可知，第3组数据集的结果与前两组数据的结果基本类似，即SAE训练收敛次数偏多，但更易找到全局最优解；当特征维度取11时，AUC能取到最大值0.992 2，此时监测精度为97.1%。因此可认为该组数据集的最佳特征维度为11。

图9为特征维度分别为1、2和3时的可视化结果。当特征维度取1时，在异常分数接近于0的区域，存在明显的误判，这说明1维特征不能反映数据的本质特征。图9b、c可发现，正常数据主要集中在3个区域，这说明了数据中包含3类正常数据，异常数据主要分布在正常数据周围，并且误判主要集中在正常数据附近。

图6 案例2 AUC和训练迭代次数与特征维度的关系Fig.6 AUC and training iteration under different feature dimensions for case 2

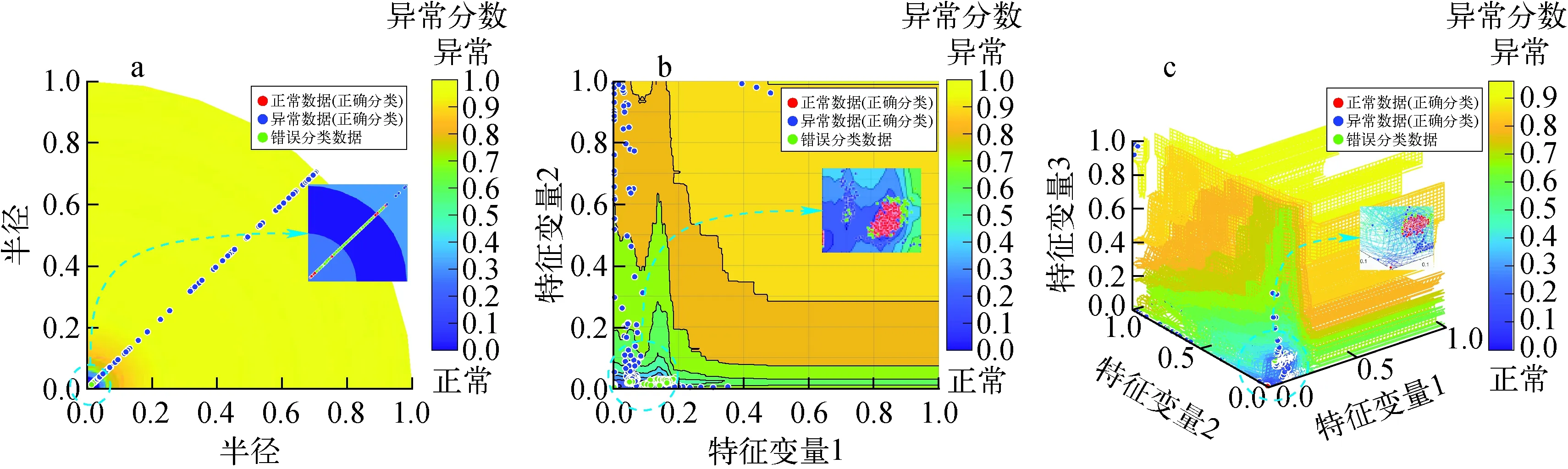
图7 案例2当特征维度为1(a)、2(b)、3(c)时的可视化结果Fig.7 Visualization results for feature dimensions taken as 1(a), 2(b) and 3(c) for case 2

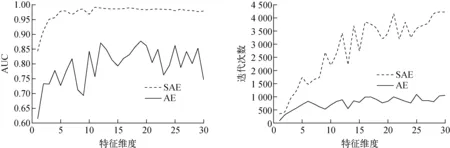
图8 案例3 AUC和训练迭代次数与特征维度的关系Fig.8 AUC and training iteration under different feature dimensions for case 3

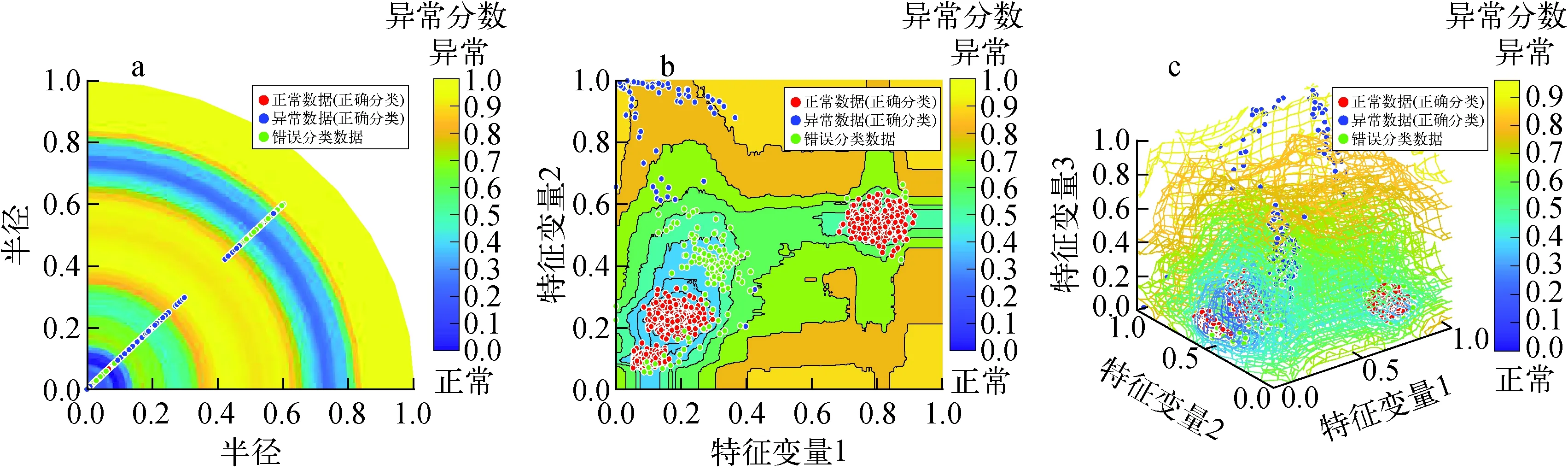
图9 案例3当特征维度为1(a)、2(b)、3(c)时的可视化结果Fig.9 Visualization results for feature dimensions taken as 1(a), 2(b) and 3(c) for case 3

3 结论

本文提出了基于SAE的特征提取方法，并将其应用于核动力装置状态监测中。在保证较高的状态监测精度和较低的训练迭代次数的条件下，实现对原始数据的特征提取。在案例1中，将包含1种正常工况的原始数据压缩成3维数据，此时AUC可取到最大值1，并实现100%状态监测精度。在案例2中，将包含两种正常工况的原始数据压缩成4维数据，此时AUC取到最大值0.994 9，并实现98%的监测精度。在案例3中，将包含3种正常工况的原始数据压缩成11维数据，此时AUC取到最大值0.992 2，并实现97%的监测精度。通过将3个案例中SAE与AE的特征提取结果进行对比可发现，SAE得到的结果相对较稳定，不易陷入局部最优解。同时，通过可视化作图，将降维结果与状态监测结果结合，可直观分辨特征提取结果优劣。综上所述，基于SAE的特征提取方法的优势主要体现在：1) 可提取原始数据在低维空间中的特征，实现高维数据向低维空间的转换，从而节约计算资源；2) 训练过程中不易陷入局部最优解；3) 将样本的本质特征信息凝聚到低维空间，从而提高状态监测的精确度。