固-固二元复合材料等效导热系数模型研究综述及评价

2020-05-07钱立波余红星孙玉发李仲春

原子能科学技术 2020年3期

钱立波，余红星，孙玉发，邓坚，吴丹，李仲春，黄涛

(中国核动力研究设计院核反应堆系统设计技术重点实验室，四川成都 610041)

等效导热系数(ETC)是表征复合材料传热性能的主要参数，是反映复合材料宏观导热能力的特征参数。在反应堆工程领域，常见的复合材料(结构)包括高温气冷堆球床、聚变堆氚增殖层、弥散燃料元件(耐事故全陶瓷微封装燃料(FCM)、金属微封装燃料(M3)和陶瓷金属燃料(CERMAT)等)等固-气/液、固-固复合材料。复合材料等效导热系数是各相导热系数、结构、排列方式及分散相体积填充率的函数。因此，根据分散相成分和结构等特点，复合材料等效导热系数计算模型可能具有不同的形式。目前，国内外众多学者根据现有经验和理论模型、最小热阻法、热阻网络法、数值计算法、渐进均匀化方法、逾渗理论和分形理论建立了多种预测二元复合材料等效导热系数的理论方法[1-2]，但这些方法在预测复合材料等效导热系数时仍存在较大的不确定性[3]，原因在于这些模型大多仅适用于特定的复合材料体系，普适性不高。因此，在应用等效导热系数模型分析复合材料导热问题前，应评价等效导热系数模型的适用性。

本文对目前固-固二元复合材料等效导热系数计算方法进行总结，并基于国内外颗粒状分散相固-固二元复合材料等效导热系数实验或数值计算结果评价已有经验或理论模型，以确定不同工况下预测精度较好的等效导热系数经验或理论计算模型。

1 固-固二元等效导热系数模型综述

Tsotsas等[2]指出，影响颗粒状分散相复合材料等效导热系数ke的参数包括连续相导热系数kc、分散相导热系数kd、分散相填充率φ及分散相特征a(大小、形态、分布及排列方式)，故二元复合材料等效导热系数模型一般具有如下形式：

ke=ke(kc，kd，φ，a)

(1)

本文主要介绍固-固二元复合材料等效导热系数6种预测方法[4]：经验或理论模型、最小热阻法、热阻网络法、数值计算法、渐进均匀化方法、逾渗理论方法(分形理论多用于多孔介质等效导热系数计算，因此本文不涉及分形理论)，并着重介绍目前广泛应用的等效导热系数经验或理论模型。

1.1 经验或理论模型

1) Lichtenecker模型

基于分散相随机分布的假设，等效导热系数的加权几何平均模型如下：

(2)

2) Maxwell模型

Maxwell[5]假设分散相为球型颗粒且随机分布，同时假设分散相颗粒温度不影响邻近分散相颗粒的温度分布，通过求解分散相颗粒随机均匀地分布在连续相中的导热问题获得了Maxwell模型。因此Maxwell模型(式(3))理论上仅适用于低填充率(φ≤0.1)或高填充率(φ≥0.9)工况。

(3)

其中，κ为分散相导热系数kd与连续相导热系数kc之比，即κ=kd/kc。

式(3)理论上适用于分散相导热系数小于连续相的工况，即κ<1，为常规Maxwell模型(R-Maxwell)；当分散相导热系数大于连续相导热系数，即κ>1时，采用反相等效导热系数模型(I-Maxwell)，即式(4)：

(4)

当分散相为球型时，Fricke模型[6]、Hamilton-Crosser模型[7]与Maxwell模型具有相同的表达形式。

式(3)、(4)也分别是Hashin-Shtrikman模型[8]的上限和下限：当κ<1时，式(3)为上限，式(4)为下限；当κ>1时，式(4)为上限，式(3)为下限。

3) Bruggeman理论模型

基于平均场理论，Bruggeman[9]基于分散相在均质连续相中随机分布的假设，通过逐次增加分散相的方法(单次增加极少量分散相)求解高填充率下二元复合材料的热导率，具有Maxwell方程的微分形式，通过再积分开发了二元复合材料等效导热系数计算模型：

(5)

Bruggeman理论模型适用于球型颗粒，填充率较高时拟合结果较好。

4) 有效介质理论模型(EMT模型)

EMT模型[10]基于分散相随机分布的假设，且与分散相形状无关，表达式如下：

(6)

其中，A=[3φ-1+(2-3φ)/κ]/4。EMT模型适用范围为：φ≫0。

5) Chiew-Glandt模型

Chiew和Glandt[11]修正了Maxwell模型，使其具有φ2的二阶精度，表达式如下：

(7)

其中，β为约化极化率，β=(κ-1)/(κ+2)。Chiew-Glandt模型适用范围为：φ=0.15～0.85，κ=10-3～104。

6) Zehner-Schlünder模型

Zehner和Schlünder[12]应用传质/传热相似的特性模拟分散相颗粒间的联系，基于基础单元获得了等效导热系数模型，Hsu等[13]对Zehner-Schlünder模型进行了修正，表达式如下：

(8)

7) Lewis-Nielsen模型

Lewis和Nielsen[14]通过修正Halpin-Tsai公式，并考虑了分散相的形状和排列方式，获得了适用于球型分散相的等效导热系数半理论模型：

(9)

Lewis-Nielsen模型适用于中等大小填充率(小于0.4)，对更高的填充率，Lewis-Nielsen模型计算结果不稳定。

8) Levy模型

Levy[15]通过引入一个附加系数修正Maxwell模型，该附加系数是分散相和连续相导热系数比κ的函数，其表达式如下：

(10)

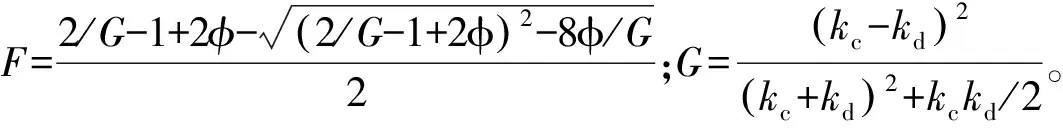
9) Agari模型

Agari等[16]认为复合材料的导热模式可分为串联(垂直导热)和并联(平行导热)两种模型。

当分散相和连续相层向与热流密度方向垂直时，等效导热系数最大，即体积平均导热系数模型：

ke=(1-φ)kc+φkd

(11)

当分散相和连续相层向与热流密度方向平行时，等效导热系数最小，即调和平均导热系数模型：

(12)

并联模型高估了等效导热系数，串联模型低估了等效导热系数，因此实际的等效导热系数介于并联模型和串联模型之间。Agari考虑了分散相的影响因素，并假定分散相均匀分布，获得了二元等效导热系数理论模型：

lnke=φC2lnkd+(1-φ)ln(C1kc)

(13)

其中：C1为影响结晶度和聚合物结晶尺寸因子；C2为形成分散相导热链自由因子。C1和C2需根据实验结果确定，且直接决定了模型预测精度。

10) Samantray模型

Samantray等[17]基于单位结构逼近(等温)和半经验场方程，获得了宽广范围κ和φ的二元复合材料等效导热系数模型[18]：

(14)

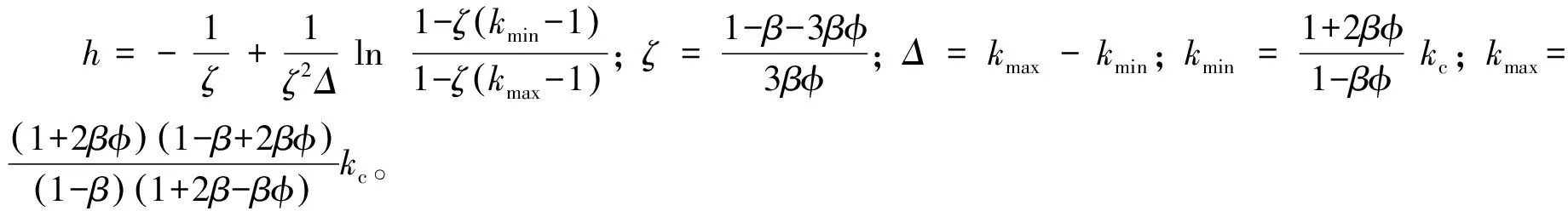
Samantray模型适用范围为：κ<20，φ=0.1～0.9。

11) Budiansky理论模型

Budiansky[19]针对N种随机分布的各向同性复合材料给出了等效导热系数的隐式方程：

(15)

12) Cheng-Vachon理论模型

Cheng等[20]基于Tsao的概率模型[21]，假设分散相颗粒服从高斯分布，以连续相的体积分数为变量的函数作为高斯分布的分布函数，通过分布函数预测二元复合材料的等效导热系数。

当kc>kd时：

(16)

当kd>kc时：

(17)

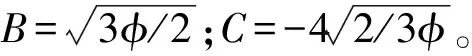
13) Singh理论模型

Singh等[22]假设分散相为刚体且形状分别为立方体或球型，通过引入一个孔隙率修正项，分别给出了立方体分散相和球型分散相等效导热系数模型。

当分散相为立方体时：

(18)

当分散相为球型时：

(19)

其中，F=1-exp(-0.92φ2ln(kd/kc))。

14) Bhattacharya理论模型

Bhattacharya等[23]针对高孔隙率泡沫金属材料开发了等效导热系数模型：

(20)

其中，F=0.35。

1.2 最小热阻法

假设分散相在复合材料中均匀分布，因此，可将复合材料视为由大量中心包含1个分散相颗粒的导热单元组成。根据最小热阻力法则和比等效导热系数相等法则，若复合材料的单元体与总体有相等的比等效热阻，则无论单元体的尺度大小，该单元体与总体的导热系数相等[24]。因此，复合材料等效导热系数的计算就归结为单元体的等效热阻的计算[25-27]。根据傅里叶导热定律，复合材料等效热阻Re为：

Q=ΔT/Re，Re=L/Ake

(21)

其中：Q为热流；ΔT为温差；L和A分别为单元体的长度和面积。

在计算单元体等效热阻时，可将单元体分为若干个微元块，形成热阻的网络图，然后根据式(21)计算微元块的热阻，单元体的等效热阻即可通过各微元体热阻的串、并联计算。

应用最小热阻法求解等效导热系数是基于复合材料是由周期性分布的等效单元体组成的，这忽略了分散相分布空间结构的影响，且未考虑分散相之间的相互作用，会低估复合材料高填充率下的等效导热系数，仅适用于中低填充率下等效导热系数的预测。

Russell[28]根据热传导与电导的相似性原理，假设分散相是分散在连续相中的具有相同尺寸、相互间没有任何作用的立方体，获得了二元复合材料等效导热系数模型：

(22)

Topper[29]应用并联电阻网络方法获得了圆球分布于立方体中的等效导热系数模型：

(23)

1.3 热阻网络法

基于热电比拟理论，可将热流当作电流、热阻当作电阻、温压(温度差)当作电压，通过将复合材料空间离散，每个空间离散单元体对应1个热阻，因此复合材料内部可看作1个热阻网络，可运用电路计算方法计算复合材料的复杂导热问题。

为得到xi方向的等效导热系数，假定其余边界上为绝热边界，xi方向上维持恒定的温度，则根据傅里叶导热定律可得[30]：

(24)

其中：∑q为xi方向的总热流；ΔT为xi方向上的总温差；N为xi方向离散单元体个数。

热阻网络法的特点是方法简单，与实验一致性较好，适用于不同的分散相形状[30-31]，相较于最小热阻法更精确，是计算颗粒分散相复合材料等效导热系数的较为有效的方法。但相比于最小热阻法，热阻网络法计算较复杂且计算量大幅增加。

1.4 数值模拟方法(傅里叶定律计算法)

颗粒填充型复合材料是非均质体系，但可将其看作由周期性的代表性体积元组成。代表性体积元一方面应充分大，能代表复合材料的微观不均匀性，另一方面应足够小，以便可将复合材料当作连续体处理[32]。将数值模拟方法应用于代表性体积元上，基于傅里叶定律可得到复合材料的等效导热系数等宏观等效特性。

稳态导热工况下，代表性体积元的温度和热流密度满足以下方程：

(25)

(26)

其中：ke,i为xi方向的等效导热系数；T为温度；qi为热流密度。在代表性体积元xi边界上给定非周期性和非对称边界，在其余边界上给定周期性或对称边界。

求解式(25)，即可得到代表性体积元中的温度和热流密度分布，则等效导热系数可由下式计算：

(27)

与理论模型相比，数值模拟方法更为灵活，能获得复合材料代表性体积元中精细的温度场来反映复合材料的宏观响应特性(等效导热系数)，并可用于分析分散相颗粒尺寸、形状、填充率、排列方式及界面状况等因素对复合材料等效导热系数的影响。目前广泛应用的数值模拟方法主要包括有限差分法[33]、有限元方法[32,34-36]和Monte Carlo方法[37-38]。由于复合材料中的分散相实际在连续相中的局部填充率和排列方式差异，代表性体积元的选取是决定等效导热系数计算精度的关键因素，这也限制了基于代表性体积元的数值模拟方法的适用范围。

1.5 渐进均匀化方法

均匀化方法[39]以连续介质理论为基础，假设复合材料由周期性单元体在空间中堆积而成，采用摄动理论对温度场按单元体尺度小参数展开，从而近似得到复合材料的等效导热系数。

针对复合材料单元体[39]，考虑周期性温度边界条件，通过求解微观控制方程，为宏观尺度(x)下复合材料等效热传导系数ke与单元体(V)下微结构关系建立了严格的计算公式：

(28)

传统的渐进均匀化方法[39-40]首先在周期性边界条件下求解得到热流密度，并通过稳态传热有限元计算得到特征温度场，最终将特征温度场根据式(28)进行单元体上积分得到等效导热系数。

均匀化方法既能从细观角度分析复合材料的等效导热系数，又能从宏观尺度分析复合材料的传热特性。当单元体相对于复合材料足够小时，均匀化方法能给出精确的预测结果。姜馨等[41]运用均匀化的方法，通过有限元法研究了弥散型燃料颗粒排列方式、填充率等因素对弥散燃料等效导热系数的影响。

1.6 逾渗理论方法

填充型复合材料的颗粒分散相在连续相中的分布是无序、随机的，其等效导热系数与分散相颗粒的填充率等因素相关，并具有逾渗网络结构的特征，即当颗粒分散相达到特定的填充率(逾渗阈值)时，复合材料等效导热系数会发生突变。逾渗理论即是处理此类强无序和具有随机几何结构系统的一种有效理论方法，通过引入一个直观的模型来处理无序体系中由相互关联程度的变化引起的效应。

陶国良[42]借鉴Mamunya等[43]根据逾渗理论获得的复合材料等效导电率的经验公式，获得了等效导热系数逾渗方程：

(29)

其中：φc为临界填充率；ke,c为临界填充率φc下的等效导热系数；n为逾渗网络因子，表示填料在连续相中形成导热网络的难易程度，与分散相大小、形状及分布特性有关。

王亮亮[44]基于逾渗理论，构建了二元复合材料“海岛-网络”模型，并建立了逾渗等效导热系数方程：

(30)

逾渗理论方法适用于分散相导热系数远大于基体相导热系数的复合材料，对不同的二元复合材料，由于分散相和连续相的差异及成型工艺条件的差异，式(29)、(30)中的φc、n、F、t等参数也会有相应的变化。因此，本文不评价基于渗透理论方法的固-固二元等效导热系数模型。

2 等效导热系数经验或理论模型对比

图1为分散相导热系数小于连续相(κ=0.05)和大于连续相(κ=20)导热系数工况下等效导热系数随填充率φ的变化趋势。从图1可见，各等效导热系数模型间预测结果差异很大，但大部分预测结果位于Hashin-Shtrikman(H-S)模型的上限和下限(R-Maxwell模型和I-Maxwell模型)之间，Hashin-Shtrikman模型的上下限又位于并联模型和串联模型预测结果之间。

根据计算结果，串联模型、并联模型、Maxwell模型、R-Maxwell模型、Bruggeman模型、EMT模型、Levy模型、Topper模型、Bhattacharya模型在整个填充率范围(0≤φ≤1)内的预测结果具有自洽性，即当φ=0时，ke=kc，当φ=1时，ke=kd，当0<φ<1时，ke位于kc和kd之间；对Zehner-Schlünder模型和Samantray模型，除φ=0和φ=1外，均具有自洽性；其余模型，如Chiew-Glandt模型、Lewis-Nielsen模型、Russell模型、Singh模型在较高填充率下，Budiansky模型在较低填充率下均不具有自洽性。

3 等效导热系数经验或理论模型评价

参考Hamilton[45]的方法，根据κ值将固-固二元复合材料分为4种类型。1) 类型Ⅰ：kd≪kc或κ<0.01，类型Ⅰ实验数据较少，故本文不涉及类型Ⅰ复合材料等效导热系数模型评价。2) 类型Ⅱ：kd≫kc或κ>100，以金属填充树脂聚合物复合材料为代表。3) 类型Ⅲ：0.01<κ<1，以耐事故燃料芯块(如FCM燃料、M3燃料及CERMAT燃料)为代表。4) 类型Ⅳ：1<κ<100，以导电橡胶复合材料为代表。

在评价等效导热系数模型时，采用3种评价准则来评价各经验或理论模型。

1) 一元线性回归方法[46]

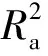
(31)

其中，R2为判定系数。

(32)

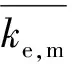
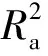
2) 平均相对误差e[46]

(33)

其中，e表征模型预测平均精度，e越小，模型预测结果越好。

3) 残余标准差σ[46]

(34)

其中，σ表征模型预测值相对于实验或数值计算值的波动大小，σ越小，模型预测结果越好。

3.1 类型Ⅱ固-固复合材料

类型Ⅱ固-固二元复合材料等效导热系数评价实验数据基于Bigg[47]、Sundstrom等[48]、Agari等[16]和王亮亮[44]中列出的实验数据以及基于Kumlutas等[34]和Folsom等[35]的数值模拟结果。表1列出了类型Ⅱ复合材料等效导热系数预测精度较高的模型。

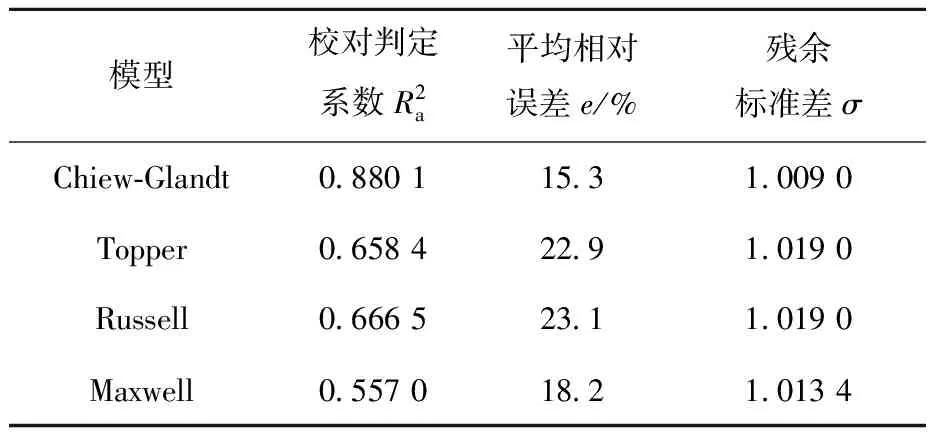
表1 类型Ⅱ固-固二元复合材料ETC模型评价结果Table 1 Evaluation result of ETC modelof type Ⅱ solid-solid binary composite

从表1可看出，Topper模型和Russell模型的校对判定系数大于Maxwell模型，但平均相对误差较大，这是由于Topper模型和Russell模型预测结果的最小二乘拟合曲线与理想拟合曲线的相似程度较高。Chiew-Glandt模型在3种评价准则下的预测结果均最好。图2为等效导热系数的Chiew-Glandt模型结果与实验结果对比。

图3为ke/kc的各模型预测结果与实验或数值结果随填充率的变化。可见，在较低填充率(φ<0.5)下，各模型预测结果差异不大，可较好地预测数值计算结果，但均低估了实验结果；随着填充率的升高，Chiew-Glandt模型的预测结果大于其余模型预测结果，与实验结果符合最好，Topper模型和Russell模型预测结果几乎相同，Maxwell模型预测结果最小。

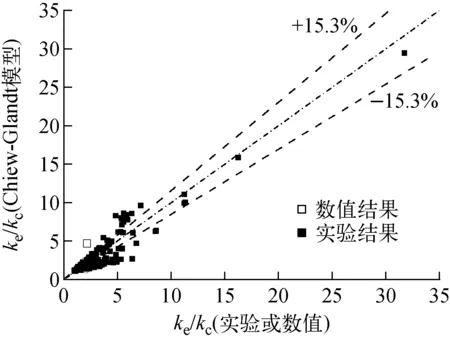
图2 Chiew-Glandt模型结果与类型Ⅱ复合材料实验及数值结果对比Fig.2 Comparison of Chiew-Glandt model prediction with experimental and numerical data for type Ⅱ composite

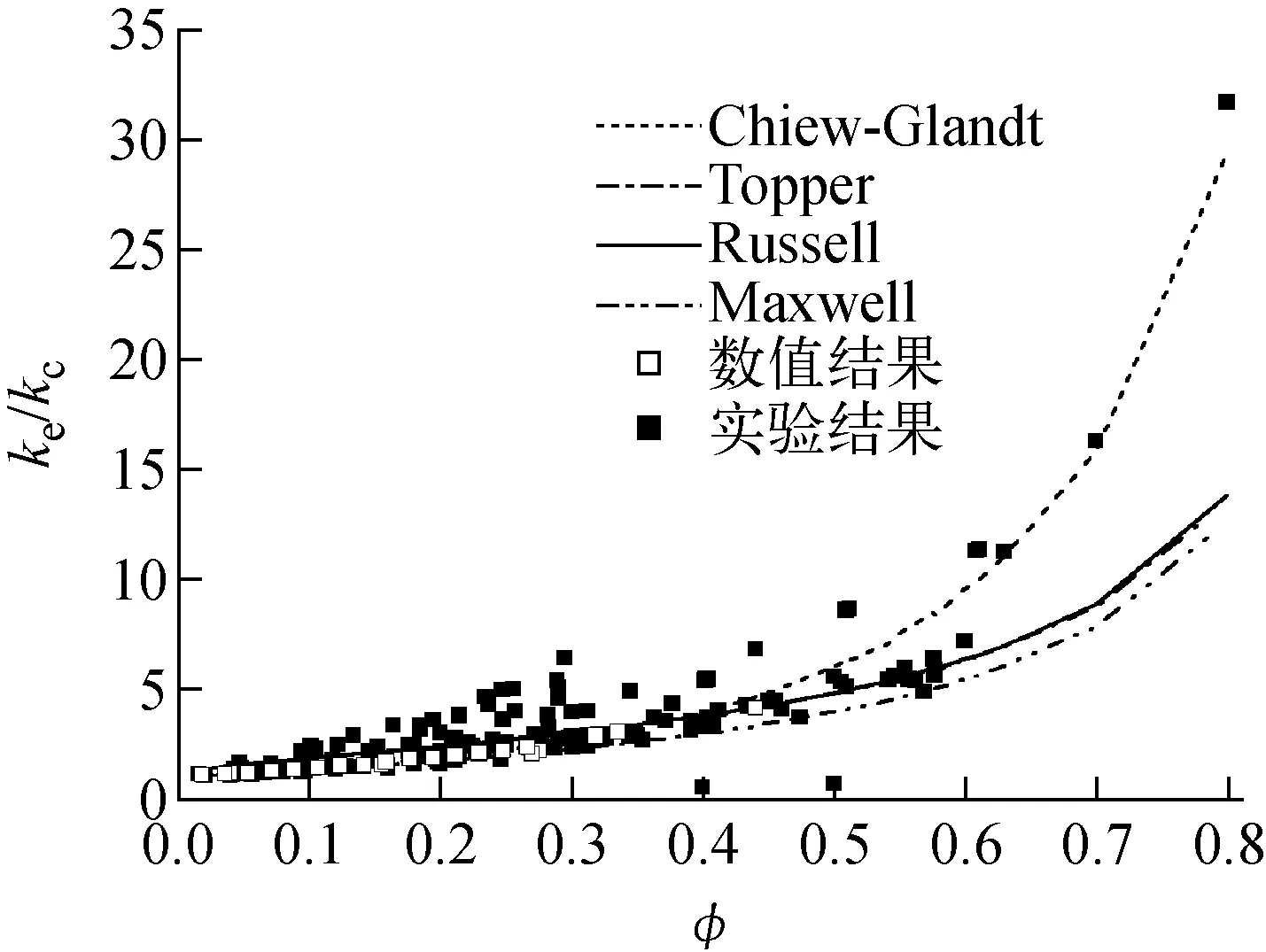
图3 不同填充率下各等效导热系数模型计算结果与类型Ⅱ复合材料实验及数值模拟结果对比Fig.3 Comparison of various ETC models prediction with experimental and numerical data as a function of volume fraction for type Ⅱ composite

3.2 类型Ⅲ固-固复合材料

目前针对类型Ⅲ等效导热系数的研究多集中在数值模拟[34-35,37,41]，仅有少数实验研究[49]。表2列出了各模型中对类型Ⅲ复合材料等效导热系数预测精度较高的模型。由表2可知，Maxwell、Chiew-Glandt、Bruggeman、Cheng-Vachon和Tropper模型均可用于预测类型Ⅲ复合材料的等效导热系数(平均相对误差均在5%以内)，其中Maxwell模型预测误差在1%以内，具有最小的平均误差和残余标准差(图4)。

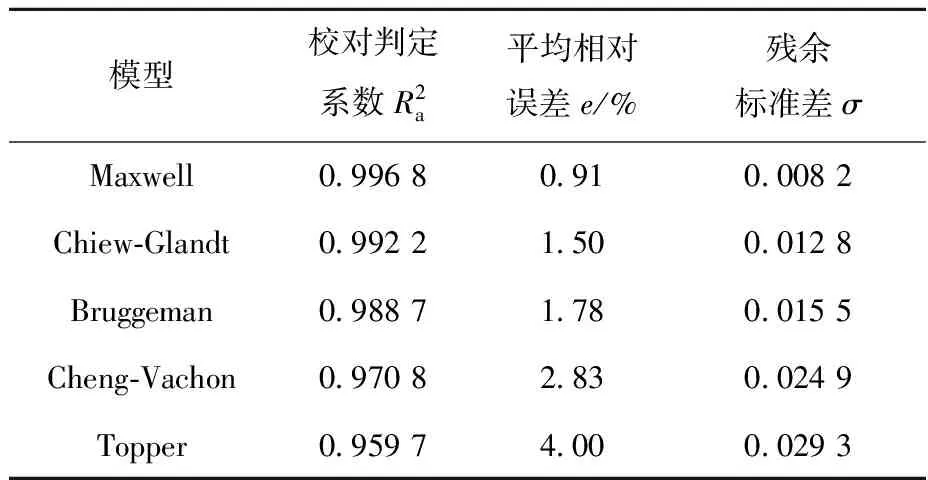
表2 类型Ⅲ固-固二元复合材料等效导热系数模型评价结果Table 2 Evaluation result of ETC modelof type Ⅲ solid-solid binary composite

图4 Maxwell模型结果与类型Ⅲ复合材料实验及数值结果对比Fig.4 Comparison of Maxwell model prediction with experimental and numerical data for type Ⅲ composite

图5为各模型计算结果与类型Ⅲ复合材料实验或数值结果随填充率的变化。可见，当填充率较低(φ<0.3)时，Maxwell、Chiew-Glandt、Bruggeman、Cheng-Vachon模型结果均与实验或数值结果差异很小；当填充率增大时，Chiew-Glandt、Bruggeman、Cheng-Vachon模型结果与实验或数值结果差值增大；Tropper模型在整个填充率范围内均高估了等效导热系数。

3.3 类型Ⅳ固-固复合材料

类型Ⅳ复合材料等效导热系数评价的数据包括数值结果[37]和实验数据[17,22,50]。表3列出了对类型Ⅳ复合材料等效导热系数预测较好的几个模型。从整体来看(实验结果和数值结果)，Chiew-Glandt、Bruggeman、Cheng-Vachon、Zehner-Schlünder及Maxwell模型的平均相对误差均低于10%；若仅考虑数值结果，Lewis-Nielsen模型和Chiew-Glandt模型的预测结果较好；若仅考虑实验结果，Bruggeman模型和Zehner-Schlünder模型的预测精度较好。

图6为Chiew-Glandt模型结果与类型Ⅳ复合材料数值结果和实验结果对比、Lewis-Nielsen模型结果与数值结果对比以及Bruggeman模型结果与实验结果对比。

图5 不同填充率下各等效导热系数模型结果与类型Ⅲ复合材料实验及数值模拟结果对比Fig.5 Comparison of various ETC model prediction with experimental and numerical data as a function of volume fraction for type Ⅲ composite

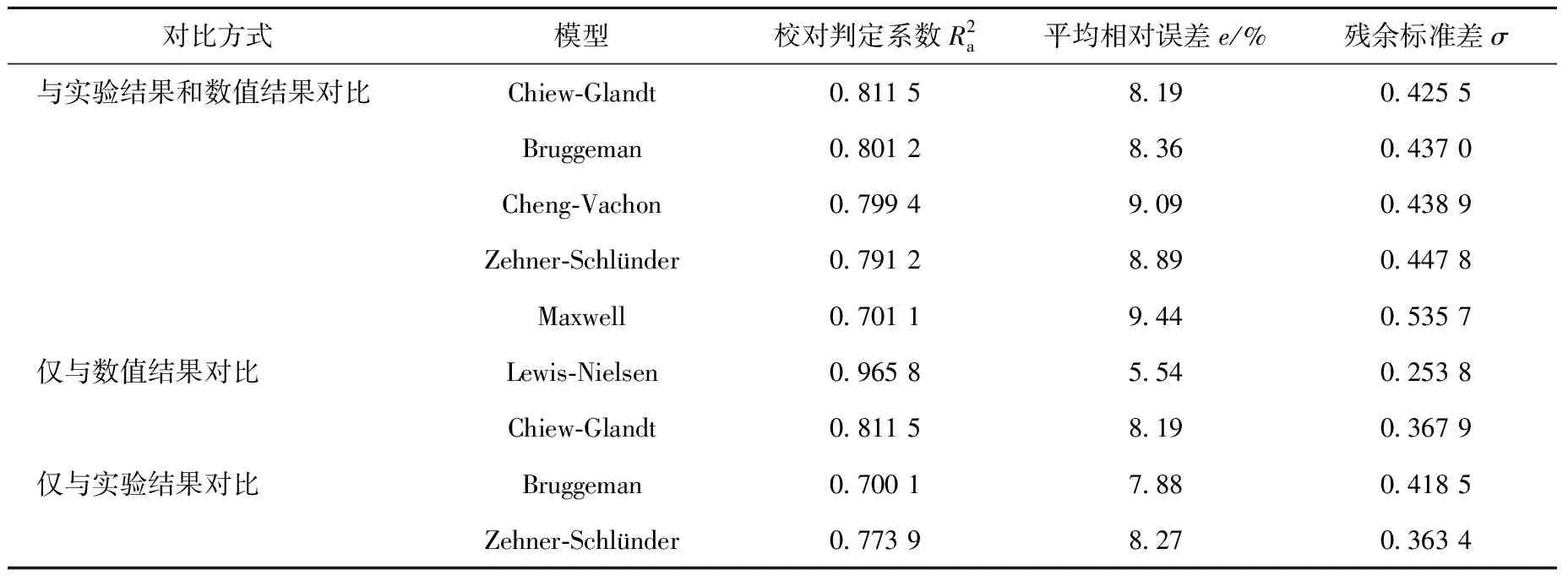
表3 类型Ⅳ固-固二元复合材料等效导热系数模型评价结果Table 3 Evaluation result of ETC model of type Ⅳ solid-solid binary composite

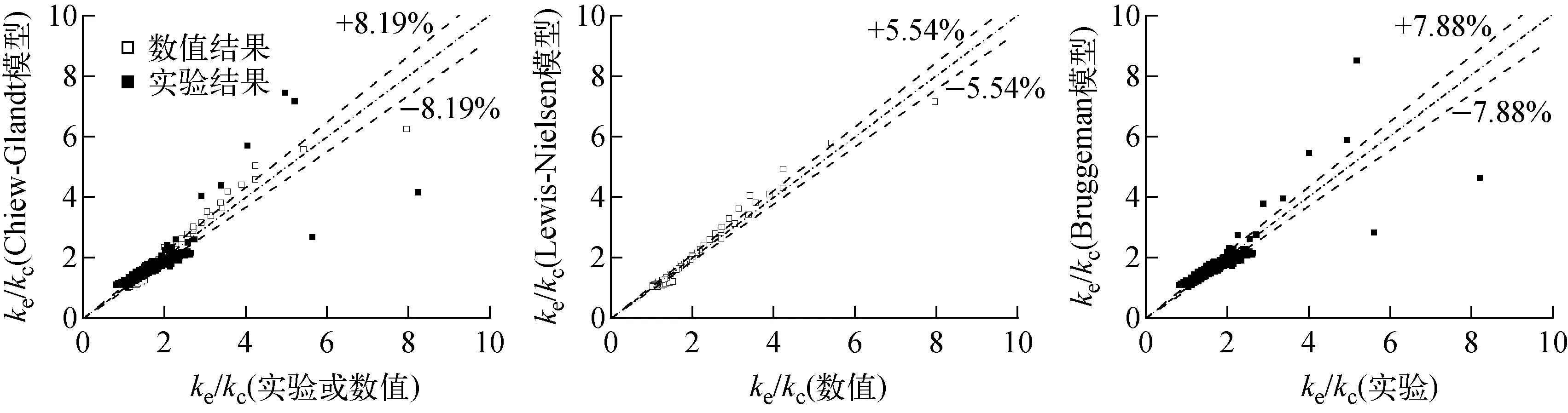
图6 等效导热系数模型与类型Ⅳ复合材料实验和/或数值结果对比Fig.6 Comparison of ETC model prediction with experimental and/or numerical data for type Ⅳ composite

图7为模型预测结果与类型Ⅳ复合材料实验结果和数值结果随填充率的变化。可见，在较低填充率(φ<0.3～0.4)下，各模型间预测结果差异不大，且预测精度较好；高填充率下，各模型间预测结果差异增大，Zehner-Schlünder模型结果大于实验和数值结果，Maxwell模型则低估实验和数值结果，Chiew-Glandt模型预测结果与实验和数值结果相差最小。

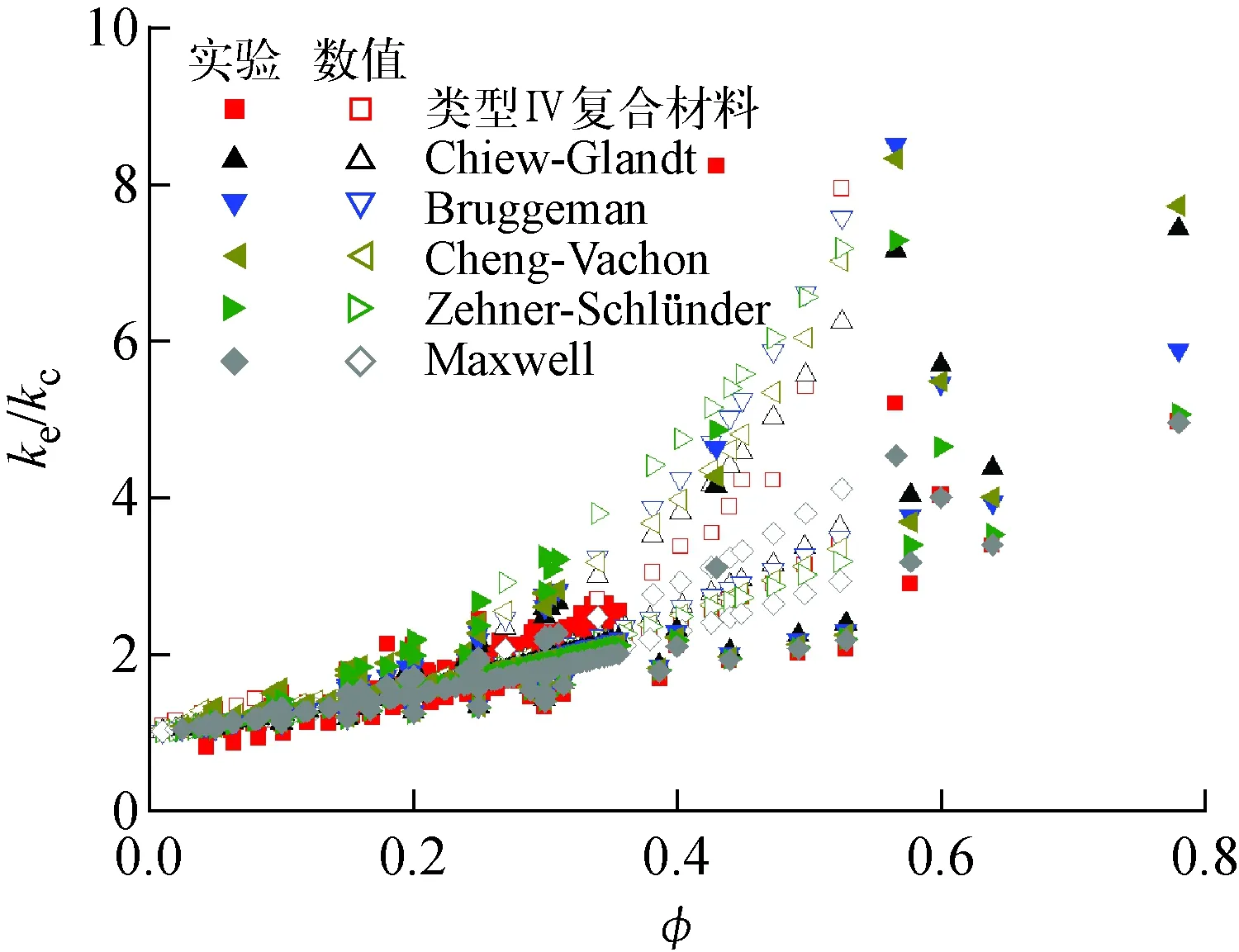
图7 不同填充率下各模型计算结果与类型Ⅳ复合材料实验结果和数值结果对比Fig.7 Comparison of ETC model prediction with experimental and numerical data as a function of volume fraction for type Ⅳ composite