ARIMA模型在江西省布鲁氏菌病发病数预测中的应用

黄玉萍，傅伟杰，熊长辉，刘晓青，胡国良

人间布鲁氏菌病(以下简称“布病”)是我国法定报告的乙类传染病，是由布鲁氏菌属细菌引起的变态反应性人兽共患病。经皮肤、消化道及呼吸道传播，临床上以长期发热、多汗、乏力、关节疼痛、肝脾及淋巴结肿大为特点，若诊治不及时，不彻底，易导致慢性感染，可遗留骨关节不可逆的器质性损害，使活动受限或出现中枢神经系统后遗症[1]，严重影响了人群健康及社会生产力，是世界上一项重要的公共卫生问题[2]。2015年江西省被国家确定为南方草地开发试点省之一，将大大促进江西省羊养殖、贩运、加工销售、餐饮等行业的发展，羊产业从业人员也将迅速增加。在目前疫情形势下，运用时间序列模型对布病疫情进行科学的预测，为布病防控提供科学依据显得十分重要。

1 材料与方法

1.1材料 发病数资料来自江西省疾病预防控制中心法定传染病报告管理系统，2014年1月至2017年12月布病月发病数作为拟合集建立模型，对2018年1月的发病数进行预测。

1.2 ARIMA模型的建立

1.2.1 模型识别

1.2.1.1序列平稳化 通过观察原始序列或差分后序列的时间序列图(拟合曲线在未来一段时间内的均值和方差不发生明显变化)、ADF检验(P<0.05)获得一个非白噪声的平稳序列，提取原序列趋势效应和季节效应[3-4]。

1.2.1.2定阶 (偏)自相关函数分别在q、p阶后截尾(几乎95%(偏)自相关系数的都落在2倍标准差范围以内)。

1.2.2参数估计 对于平稳序列,利用最小二乘法或最大似然法进行参数估计，参数估计值的显著性检验可以得出模型中的一些项是否需要，一般要求每个参数都有统计学意义。如果拟合的多个模型均通过参数显著性检验，引入赤池信息准则( Akaikes information criterion，AIC)概念，进行模型优化，以该数值小者为优[5-6]。

1.2.3模型检验 模型的残差序列自相关函数和偏相关函数均在置信区间内，且P>0.05，该序列通过残差白噪声检验，模型可用来预测。

1.3模型预测 模型预测采用均方根误差(Rood Mean Squared Error， RMSE)、平均绝对误差(Mean Absolute Error，MAE)、希尔不等系数(Theil Inequality Coefficient，Theil IC)、偏方差(Bias Proportion，BP)、方差率(Variance Proportion，VP)、协变率(Covariance Proportion，CP)等指标衡量，前5个指标越小、最后一个指标越大说明预测效果越好。模型的建立和预测通过Eviews10软件实现。点预测采用误差进行预测准确性的比较。

2 结 果

2.1江西省2014-2017年布病月发病数序列图 2014-2017年间江西省布病发病总数218例，单月最多12例，最少0例，数据整体不算平稳(见图1)。(偏)自相关图和ADF检验(P<0.05)均显示序列平稳(见图2)。用Eviews10对数据进行拟合,得到不做差分时的最优模型AR(1)，R2=0.23，AIC=5.138，RMSE=2.934，MAE=2.429，Theil IC=0.279，BP=0.002，VP=0.339，CP=0.659。

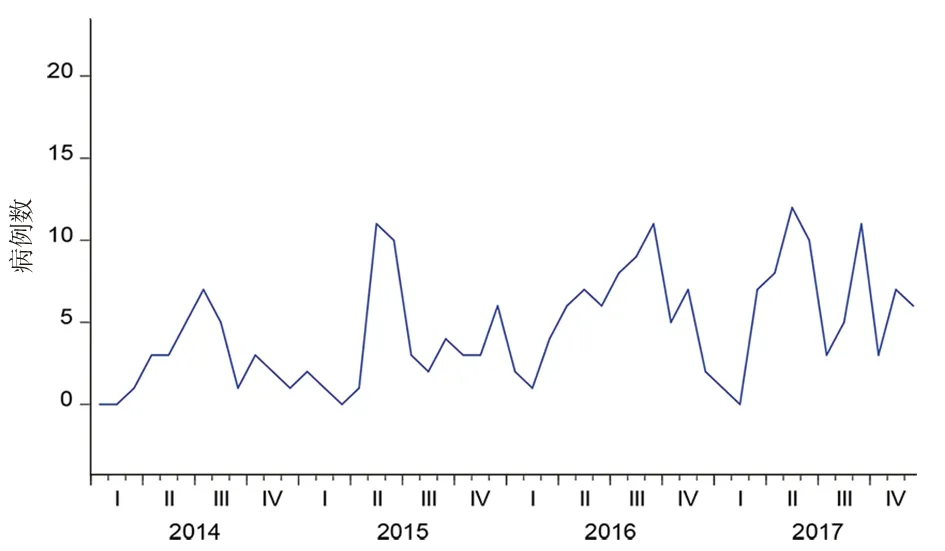
图1 江西省2014-2017年布病月发病数序列图Fig.1 Monthly incidence of brucellosis in Jiangxi Province,2014 to 2017

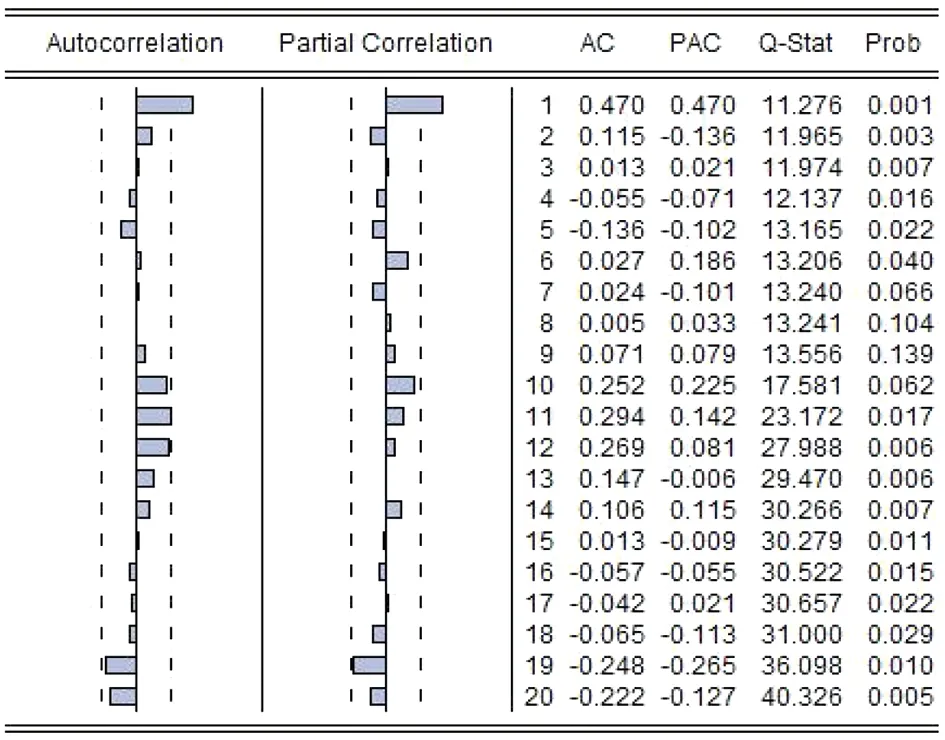
图2 江西省2014-2017年布病月发病数序列的(偏)自相关图Fig.2 ACF and PACF diagram of the number of brucellosis cases per month in Jiangxi Province,2014 to 2017

2.2一阶差分分析 用Eviews10对一阶差分后的数据进行拟合，得到最优模型ARIMA(1,1,3)，R2=0.297，AIC=5.204，RMSE=2.933，MAE=2.376，Theil IC=0.282，BP=0.053，VP=0.145，CP=0.801。

2.3二阶差分分析 用Eviews10对二阶差分后的数据进行拟合，得到最优模型ARIMA(3,2,0)，R2=0.453，AIC=5.776，RMSE=4.065，MAE=3.089，Theil IC=0.326，BP=0.0003，VP=0.044，CP=0.955。

2.4三阶差分分析 用Eviews10对三阶差分后的数据进行拟合，得到最优模型ARIMA(3,3,0)，R2=0.690，AIC=6.335，RMSE=5.299，MAE=4.247，Theil IC=0.384，BP=0.0003，VP=0.253，CP=0.747。

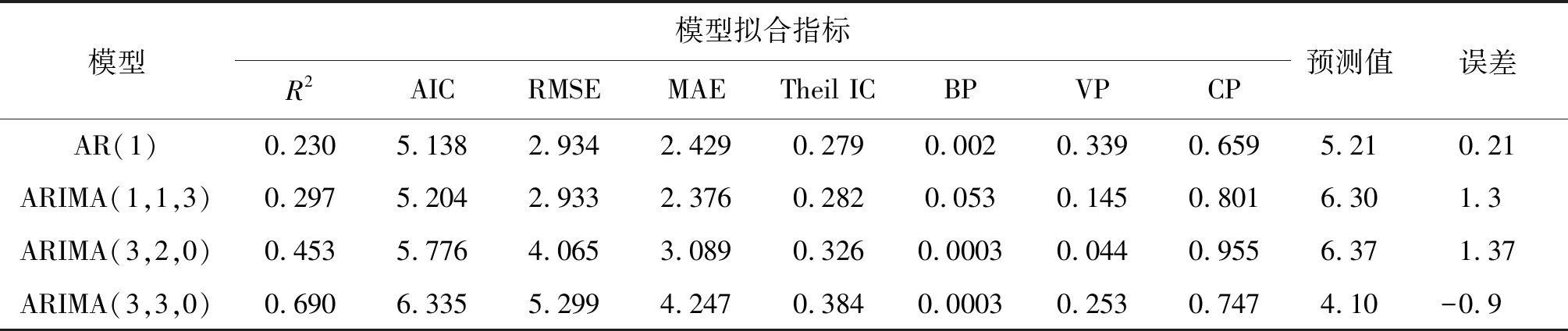
2.5模型的拟合度和预测误差分析 从拟合图(见图3)来看，拟合曲线最吻合的为ARIMA(3,3,0)，其次为ARIMA(3,2,0)；AR(1)和ARIMA(1,1,3)拟合效果较差。就各模型拟合的指标(见表1)来看，AR(1)的AIC值(5.138)和希尔不等指数(0.279)最小；ARIMA(1,1,3)的均方根误差(2.933)和平均绝对误差(2.376)最小；ARIMA(3,2,0)的偏差率(0.0003)和方差率(0.044)最小，协变率(0.955)最大；ARIMA(3,3,0)的R2值(0.69)最大。

2018年1月江西省布病报告数为5例，4个最优模型中，AR(1)的预测误差最小为0.21，其次是ARIMA(3,3,0)。抛开预测误差较大的ARIMA(1,1,3)和ARIMA(3,2,0)，比较AR(1)和ARIMA(3,3,0)，可以发现ARIMA(3,3,0)有着更吻合的趋势图和最大的R2值，而AR(1)有着更小的AIC值和希尔不等指数。

图3 四种模型拟合图的比较Fig.3 Comparison of fitting graphs of four models

表1 四种模型拟合参数的比较
Tab.1 Comparison of fitting indicators of four models

模型模型拟合指标预测值误差R2AICRMSEMAETheil ICBPVPCPAR(1)0.2305.1382.9342.4290.2790.0020.3390.6595.210.21ARIMA(1,1,3)0.2975.2042.9332.3760.2820.0530.1450.8016.301.3ARIMA(3,2,0)0.4535.7764.0653.0890.3260.00030.0440.9556.371.37ARIMA(3,3,0)0.6906.3355.2994.2470.3840.00030.2530.7474.10-0.9

3 讨 论

江西省2014-2017年布病报告总数为218例，病例多集中于5-9月，与北方地区不一致[7]。发病高峰不稳定。原因可能是布病近年来才在江西省内出现，相关医务工作者及患者对其较陌生，对于发现疾病的灵敏度不够，从而出现了诊断和报告的滞后现象。往年1月份江西省布病报告数一般为0～2例，2018年1月报告数为5例，明显超过以往水平。报告单位都是省内市级及以上医疗单位，2017年底江西省内布病病例分布覆盖所有地级市[8]，这说明各市级医疗单位对于布病有了一定的警惕性，但同时要加强县(区)级医疗机构的人员培训，以实现布病的早发现、早治疗，早处理、早报告。值得关注的是，流调报告显示该5例病例中，3例有明显的羊接触史；1例为1岁儿童，食用新鲜蒸煮过的羊奶；1例为家务待业者，无明确传染源。结合病例中非职业人群的占比由2015年的30%增长至2017年的48%，表明布病的传播形式多样，疾病的溯源和防控依然存在着较大难度。

ARIMA模型是根据数据序列偏、自相关函数建立起线性的数据间相互依赖的定量模型，整合了趋势因素、周期因素和随机误差等因素，既吸取了回归分析的优点又发挥了移动平均的长处，且只需发病资料就可进行预测，是短期预测最为成熟的时间序列预测方法之一[9-10]。

本研究探索在不同差分次数条件下创建预测模型，得出了几个最优模型。其中，AR(1)和ARIMA(3,3,0)的预测值最接近于实际值，而ARIMA(3,2,0)和ARIMA(1,1,3)的预测误差较大，说明赤池信息准则和R2值是确定最优模型的两个较好指标。另一方面，ARIMA(3,2,0)的R2、协方率和拟合图的表现都好于ARIMA(1,1,3)，预测值的误差却较大，猜测可能是由于预测误差本身存在的影响。同时，一般认为ARIMA模型法至少需要50个以上数据建模[11]，本研究只有48个数据且含有3个零值的小样本。

模型的选择很大程度上是研究者根据ACF图和PACF图再结合自身经验综合确定的相对最优模型，所以研究者给出的并不是最优模型而是基于自身经验做出的最优选择[12]。专家指出p、q的值一般不超过5，然而有研究跳出这个限制尝试建立了几个可能的模型，发现ARIMA(7,1,0)(1,0,1)12有着更小的绝对误差和相对误差(平均值<5%)，并且残差检验大于0.8提示拟合效果更好[13]。尽管ARIMA模型在很大程度上提取了时间序列信息，但原理上依然是一个线性模型。而布病的发生受不同宿主动物与传播途径等因素的影响，因此建立的预测模型并不唯一，在今后的研究中考虑在条件允许的情况下尽可能的全面收集布病发病的影响因素, 将相关因素纳入模型中提高模型精度，以达到最佳的预测效果。

利益冲突：无