基于多场耦合模型的堆石坝面板温度应力分析
2020-05-07肖曲飞程勇刚田文祥
肖曲飞,程勇刚,周 伟,田文祥,王 桥
(武汉大学水资源与水电工程科学国家重点实验室,湖北 武汉 430072)
现有研究表明,温度应力是堆石坝面板开裂的主要原因之一[1-2],因此关注混凝土面板的温控防裂问题,必须对混凝土面板进行仿真分析,在实际情况的基础上动态模拟大坝混凝土面板的温度场和应力场。但是目前国内研究混凝土水化放热过程时大多采用传统绝热温升模型,假定混凝土龄期在混凝土水化放热反应过程中为唯一影响因素[3],忽略了温度、化学、强度的耦合效应,因此在研究混凝土水化反应时应当综合考虑温度以及龄期对反应过程的影响。
利用水化度来反映水化反应程度,以此来衡量混凝土性能发展程度,国内外学者已经有了一些进展。Cervera和Oliver等人[4]提出了一种基于有限元的混凝土化学-热-力耦合模型,可以预测不同时期的水化度和水化热。Di Luzio和Cusatis[5-6]补充了一种新型水化度模型。马跃峰[7]研究了混凝土水化过程中的温度应力。周伟、冯楚桥等人[8-9]提出了一种新型混凝土水化模型,结果表明水化模型的特性更加贴合实际情况。
本文对河南天池上水库混凝土堆石坝混凝土面板进行了三维有限元数值模拟,对比研究了采用不同温升模型大坝整体施工期温度应力演变过程,探讨了目前温控防裂计算可能存在的误区。
1 计算基本理论
1.1 常规绝热温升模型
1.1.1 水化热
目前绝热温升模型在工程中常采用以下典型模型[3]:
(1)
式中:Q(t)是龄期t时的水化热;Q∞是最终水化热;n是水化热达到一半的龄期。
1.1.2 弹性模量
混凝土的弹性模量的发展如下表示[3]:
(2)
式中:E(t)是龄期t时的弹性模量;E∞是最终弹性模量;q是弹性模量达到一半的龄期。
1.2 修正的水化度化学-热-力耦合模型
1.2.1 水化热
混凝土的水化放热过程是自由水与未水化产物相结合产生水化产物的过程,假定自由水最终能够完全反应,故引入水化度来描述该反应的发展程度:
(3)
式中:ξ(t)是龄期t时水化度;m∞是完全反应后结合水质量;m(t)是龄期t时结合水质量。
根据阿伦尼乌斯定律,采用修正的水化度模型[8],水化模型如下:
(4)
(5)

混凝土的水化热公式如下:
(6)
式中:t是龄期;ξ是水化度;Q∞是最终水化热。
1.2.2 力学特性计算
1)弹性模量。混凝土弹性模量的发展过程可以描述为:
(7)
式中:E(ξ)是水化度为ξ时的弹性模量;ξ0是混凝土强度开始发展时的水化度;E∞是最终水化度的弹性模量;re是材料参数。
2)混凝土强度。混凝土抗拉、压强度的发展可以描述为[9]:
(8)
(9)
式中:f(ξ)c、f(ξ)t分别是水化度为ξ时的抗压、抗拉强度;ξ0是混凝土强度开始发展时的水化度;f∞c、f∞t分别是最终水化度时的抗压、抗拉强度;rc、rt是材料参数。
2 工程分析
2.1 有限元模型
本文着重分析面板温度应力,因此采用子模型法先对面板堆石坝整体进行变形分析,得到面板与垫层之间的脱空情况,再将混凝土面板与趾板提取出来单独计算,将面板底面的脱空节点设置成第三类边界条件,用等效的表面放热系数来考虑脱空边界条件。模型计算采用商用有限元软件ABAQUS,模型采用三维八节点实体C3D8单元,天池混凝土面板共离散为78 948个单元,110 290个节点。面板沿厚度方向剖分为六层,三维有限元计算模型如图1所示,蓝色单元为面板单元,紫色单元为趾板单元。

图1 混凝土面板三维有限元模型图
2.2 材料参数
面板混凝土采用C3090W12F150混凝土,粉煤灰掺量为25%,水灰比为0.42,砂率为38%,纤维素纤维掺量为0.9 kg/m3。常规模型混凝土热力学参数见表1。通常混凝土水化反应的热力学参数可以根据绝热温升试验的温度或水化放热量数据由以下公式推导得出:
(10)
(11)
式中:Q(t)为龄期t时水化放热量;Q∞为混凝土最终放热量;t(ξ=0.5)为水化反应进行到一半的龄期;t0为诱导期结束的龄期;ξ(t)为t时刻时的水化度。
得到混凝土水化放热量后,根据式(10)(11),结合试验数据,利用参数反演获得耦合模型所需材料参数,耦合模型材料参数见表2。混凝土参数反演结果与温度实测值的对比见图2,参数反演结果与实测值拟合较好,参数合理。

表1 常规模型热力学参数表

表2 耦合模型参数表

图2 绝热条件下混凝土温度历程曲线图
3 计算结果分析
分别采用常规模型计算方法和耦合模型计算方法对混凝土面板施工期温度场与应力场进行模拟,图3为面板常规计算结果,图4为面板耦合计算结果。对比图3与图4,两种模型仿真结果温度场与应力场规律相似,性质相同。面板底面温度沿高程向下逐渐变高,单条面板之间温度与应力分布基本一致。两种模型不同之处在于常规模型面板底面最高温度为31.45℃,最大主应力为2.45 MPa;耦合模型面板底面最高温度为30.40℃,最大主应力为2.17 MPa,均比常规模型低。造成这种差异的原因与两种模型特性有关,常规模型按差分法计算水化热,水化热在前期释放集中,28 d龄期之后水化热往往较小。耦合模型考虑了温度对水化速率的影响,水化热的完全释放需要相当长的时间。
为了更好地分析两种模型的区别,本文在面板中部同一位置沿厚度方向选取了3个代表点。应力分析中,以拉应力为正,压应力为负。图5反映了面板中部各特征点温度与应力随时间的变化情况。图6对比了两种模型混凝土弹性模量随时间的发展过程。图7反映了各特征点水化度随时间的发展过程。图8反映各特征点耦合模型混凝土强度随时间的发展过程。表3统计了各特征点重点时期的温度应力。表4对比了常规模型与耦合模型混凝土在7 d、28 d的强度值。
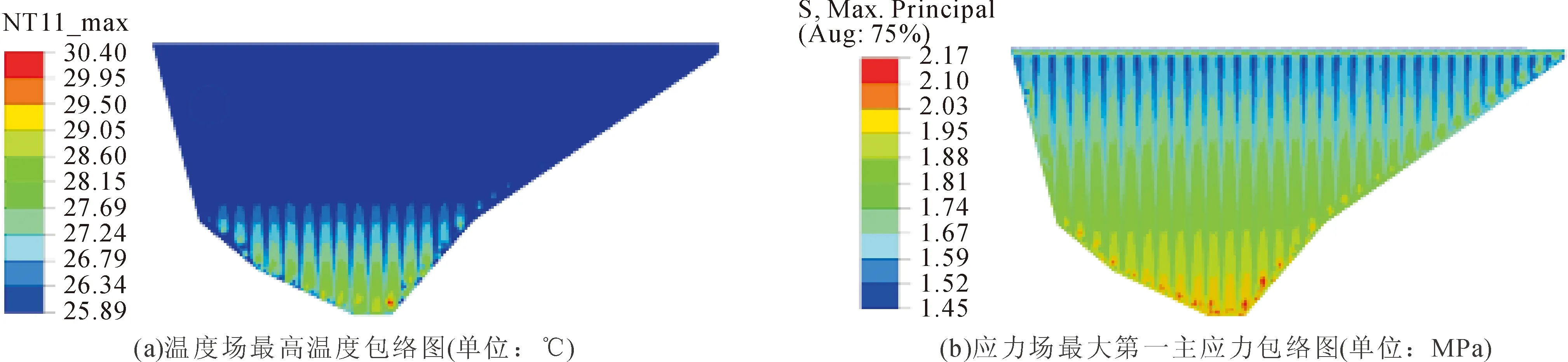
图4 多场耦合模型仿真结果图

图5 特征点温度应力历程曲线图

图6 特征点弹性模量历程曲线图

图7 特征点水化度历程曲线图
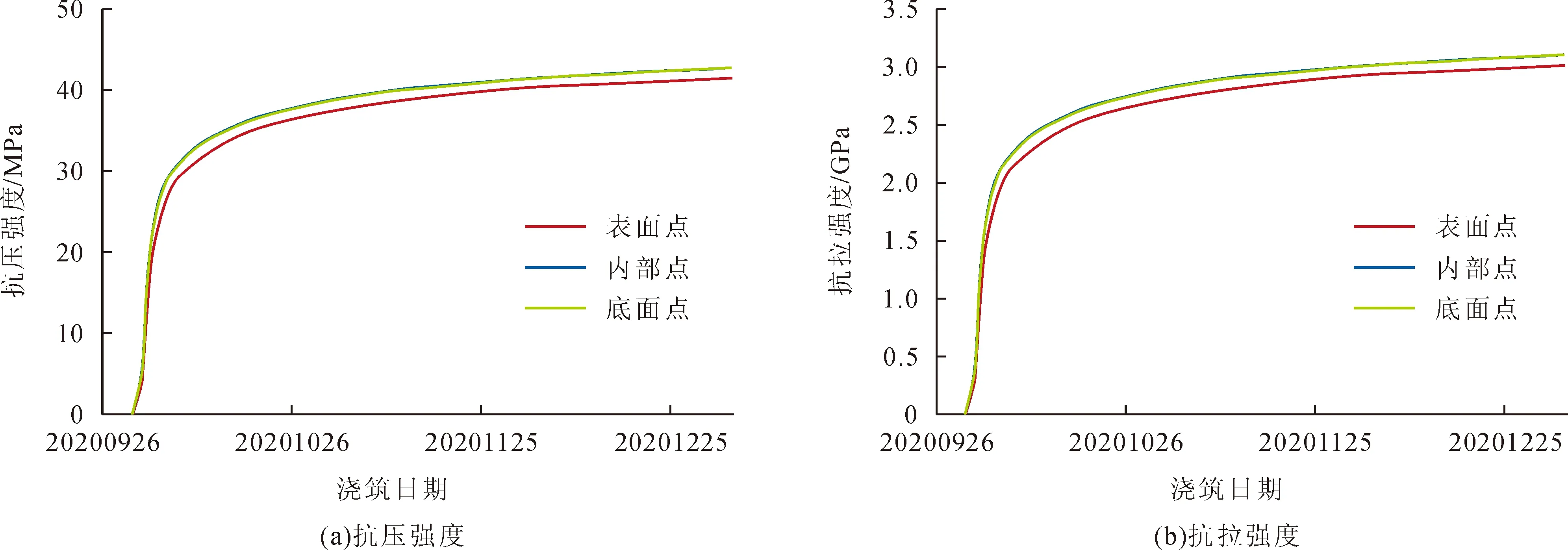
图8 特征点耦合模型强度历程曲线图
根据图5,面板混凝土在浇筑初期温度迅速上升,但由于面板较薄且在低温季节浇筑,温度上升至温升峰值后开始下降,降温幅度与气温有关。对比图5与表3,与常规模型相比,耦合模型混凝土水化反应开始后温升速率更小,同一点温升幅度更小,温升峰值出现时间也更晚,与温度场的计算结果相吻合。对比图5(a)、(b)、(c)以及表3可知,相比于面板内部与底部,面板表面直接与空气接触,散热较快,温升幅度较小,温升峰值出现较晚,因此气温下降时,混凝土的降温幅度小。根据图7,面板各部位混凝土的水化进程的发展有差异,因为温度影响了混凝土水化速率,面板各部位温度不同,水化进程的发展自然也不同。面板内部以及底部混凝土散热条件比表面散热条件差,温度较高,水化度发展快,面板表面混凝土的水化度发展滞后于面板内部的水化度。
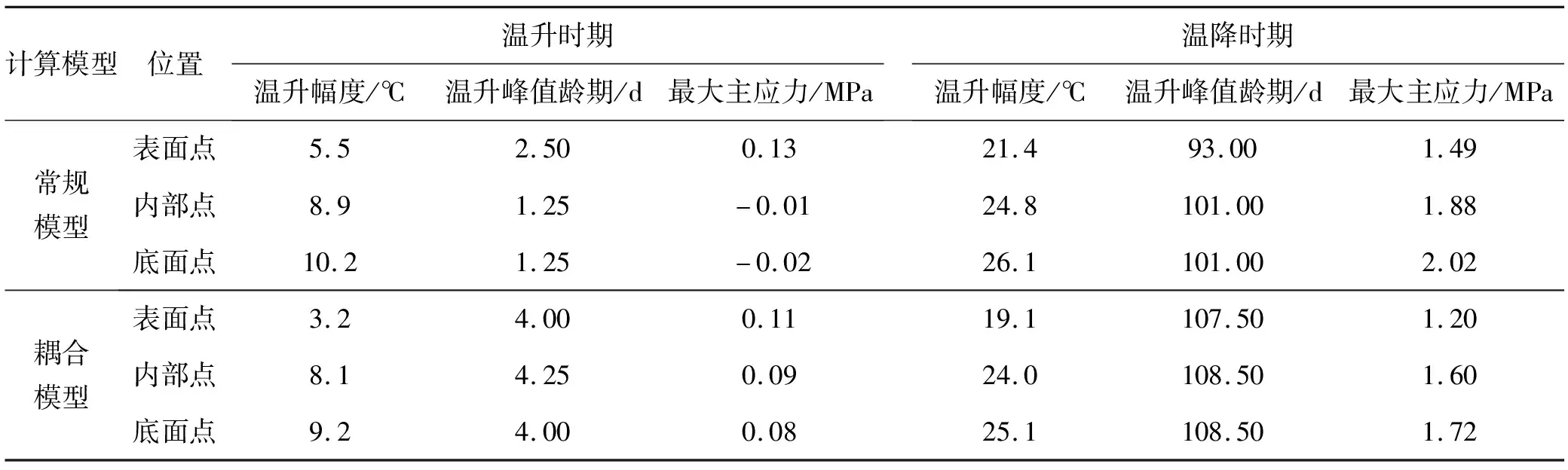
表3 特征点温度应力统计表
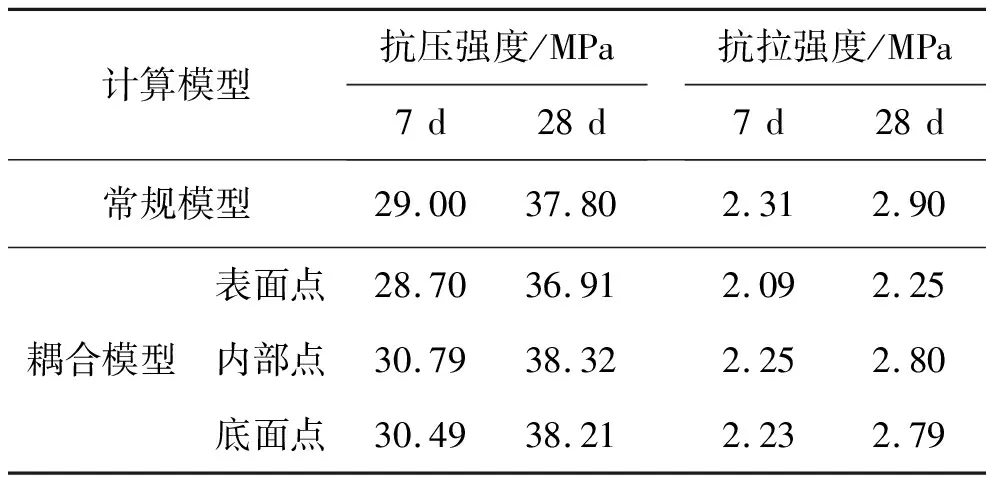
表4 特征点混凝土强度统计表
面板混凝土施工期的温度变化以及弹性模量的增长直接影响了混凝土施工期应力的发展。面板混凝土施工期应力主要由两部分组成:一是温升时混凝土内外温差产生早期应力;二是降温时混凝土受垫层与趾板约束产生应力。因此重点分析最大温升与最大温降这两个时刻。分析表3、图6,温度上升时期,当混凝土达到温升峰值时,面板内外温差产生了早期拉应力,此时混凝土弹性模量比较小,应力水平都较低。温度下降时期,拉应力最大值出现于温降峰值龄期附近,由于耦合模型混凝土弹性模量比常规模型弹性模量发展慢,弹性模量较小,且温降幅度也较小,因此耦合模型混凝土拉应力水平更低。对比图5以及表3,与面板内部相比,面板表面混凝土降温幅度小,拉应力也更小。
温度对混凝土水化过程的影响不仅体现在混凝土水化速率方面,也体现在混凝土力学特性发展方面。由图6可知,混凝土水化过程初期,耦合模型混凝土弹性模量比常规模型弹性模量发展慢,耦合模型面板表面混凝土弹性模量比内部混凝土弹性模量发展慢。结合图8与表4可知,7 d、28 d龄期时耦合模型面板表面抗压强度略小于常规模型抗压强度,内部抗压强度略大于常规模型抗压强度;7 d、28 d龄期时耦合模型面板表面抗拉强度远小于常规模型抗拉强度,内部抗拉强度略小于常规模型抗拉强度。这表明考虑温度的情况下,面板内外各部位温度分布不均匀导致面板内外混凝土水化程度不一致,进而导致面板内外混凝土弹性模量、强度等力学特性发展不一致。相比于面板内部,面板外部温度较低,水化程度发展较慢,弹性模量与强度等力学特性发展也略微滞后。另外,由表4可知,常规模型不考虑温度对混凝土水化程度的影响,面板各部分混凝土强度保持一致,而参考耦合模型的计算结果可知面板表面混凝土抗压以及抗拉强度发展滞后,故实际工程需重点关注面板内外强度发展情况,防止出现裂缝。
4 结 语
针对常规模型的不足,本文采用热学-化学-力学耦合模型,对天池堆石坝混凝土面板进行了三维有限元数值模拟。耦合模型与常规模型计算结果体现出两种模型的差异性。常规模型没有考虑温度对水化进程的影响,水化热释放集中在早龄期。耦合模型考虑了温度的影响,水化热完全释放需要较长时间,更加贴合工程实际。根据耦合模型结果,面板各部位温度分布不同,各部位水化程度也不同,各部位混凝土弹性模量、强度等力学特性发展并不一致。实际工程中可以利用耦合模型来计算面板应力水平,综合判断面板内外各部位强度发展情况,防止面板开裂。
