考虑降雨空间异质性的动态临界雨量预警指标推求

闫宝伟，刘 昱，江慧宁，李正坤，杨文发，张 俊

（1.华中科技大学 水电与数字化工程学院，湖北 武汉 430074；2.长江水利委员会水文局，湖北 武汉 430010）

1 研究背景

我国中小河流众多，且多分布于流域源头，地形地质条件复杂，防洪工程建设难度大，常出现“大雨大灾、小雨小灾”的局面。随着我国大江大河防洪体系的基本建成，中小河流的洪水防治成为我国防洪减灾的薄弱环节。近年来，受全球气候变化影响，局地强降雨增多，中小河流的洪水灾害有加剧之势，我国洪水防御的短板效应凸显。2010年国务院出台的《关于切实加强中小河流治理和山洪地质灾害防治的若干意见》中，要求各地区、各部门进一步加大中小河流治理和山洪灾害防治力度，提升水文监测预警能力。经过多年的建设，我国在中小河流洪水监测、预报预警等方面取得了长足的进步，初步建成了中小河流洪水灾害防御体系。然而，一方面，我国中小河流洪水灾害防治量多面广，治理难度大；另一方面，现有防御技术仍然存在一些亟待突破的“卡脖子”难题，如中小河流洪水预警的准确性和及时性等。本文旨在解决考虑降雨空间异质性时动态临界雨量预警指标的推求问题，进一步提高洪水预警的准确性。

中小河流洪水的预警通常可以通过建立高精度的洪水预报模型［1］，根据预报洪峰是否超过河道的警戒流量进行预警。常用的水文模型包括新安江模型、萨克拉门托模型、陕北模型、时空变源混合产流模型等集总式模型，TOPMODEL、HEC-HMS 等半分布式水文模型和MARINE、LISFLOOD、CNFF-HM 等分布式水文模型［1-3］。但一方面中小河流洪水资料缺乏，参数率定的精度难以保证；另一方面中小河流洪水的形成本身随机性就强，现有水文预报模型的模拟精度在很多地区很难达到预警的要求，如中国水利水电科学研究院针对洪水预警开发的CNFF-HM 模型在全国也仅有64%的流域能达到较高的模拟精度［2］。另一种可行的途径是通过建立与洪水密切相关的预警指标（体系），根据预警指标判断是否预警。常见的预警指标包括临界雨量、临界雨力［4-5］等，而洪水除了跟降雨量直接相关外，还受土壤含水量和降雨空间分布等的影响，因此，临界雨量应是一个与多要素相关的动态阈值，如考虑土壤含水量的动态临界雨量。相关研究表明，前期降雨较干与较湿情形下的临界雨量相比，约有30%～50%的增加［6-8］，可见，土壤含水量对临界雨量的影响非常大。土壤含水量的表示方法有多种，如前期降雨、API、土壤饱和度等，这些指标比较容易量化，现有研究也大多基于这些指标推求动态临界雨量［9-12］。除此之外，降雨的空间分布对临界雨量指标也有较大影响，罗倩等［13］采用HEC-HMS 模拟了不同降雨空间分布对临界雨量计算的影响，表明暴雨中心位于上游比位于下游的临界雨量也将有30%～50%的增加。

可见，降雨的空间分布与土壤含水量对临界雨量具有同等程度的影响。降雨空间分布的量化指标有变差系数、不均匀系数和极端比值系数等［14］，这些指标虽能反映出降雨在空间上的差异性，但无法反映暴雨中心的分布情况，指标包含的信息不够全面，无法据此直接推求动态临界雨量。因此，考虑降雨空间异质性时动态临界雨量指标的推求，关键在于提出一种能够全面量化降雨空间不均匀度和暴雨中心分布情况的指标。

2 降雨空间异质性指数

降雨的空间分布可采用多种插值方法进行分析，如泰森多边形法、反距离加权法和克里金法等，本文选取水文上应用比较广泛且易于实现的泰森多边形法进行降雨的空间分析。等流时线反映了流域汇流时间的空间分布情况，同等强度下，降雨越靠近下游，汇流时间越短，形成的洪峰越大，峰现时间越早，因此，等流时线可以间接反映降雨的空间位置。据此，本文提出了一种耦合泰森多边形法和等流时线法的降雨空间异质性指数（Spatial Heterogeneity Index of Precipitation，以下简称SHIP）。具体的推求步骤如下：

（1）假设某流域共有n 个雨量站，站点分布如图1所示，每个雨量站点的降雨量为Pi（i=1，…，n），利用泰森多边形法计算每个泰森多边形的面积权重λi（i=1，…，n），则流域面平均雨量为：

图1 泰森多边形计算等流时面面积

（2）根据栅格的汇流时间绘制等流时线，共得到m 个等流时面，按汇流时间由小到大记每个等流时面相对于流域的面积比为 fj（j=1，…，m），统计每个等流时面内各个泰森多边形的面积，设其占流域面积的比例分别为ri，j，则：

每个等流时面的面平均雨量为：

（3）按照汇流时间由小到大，以等流时面相对面积 fj的累加值为横坐标，以相应等流时面的平均雨量Rj的累加值为纵坐标绘制降雨量的空间分布曲线，如图2所示。若降雨量为均匀分布，则该曲线退化为图中的直线OL，L 点的纵坐标即为流域的面平均降雨量（本例为50 mm）。若降雨中心在下游，则曲线位于OL 的上方，如图中实线所示；反之，若降雨中心在上游，则曲线位于OL 的下方，如图中虚线所示。曲线越弯曲，表明降雨的空间分布越不均匀。若记降雨空间分布曲线与OL间的面积为A，且降雨空间分布曲线在OL 的上方时，A 为正，反之为负，OL 与横坐标轴及右边框围成的面积为B，则可用A 与B 的比值反映降雨空间分布的不均匀程度。由此，定义降雨空间异质性指数：

式中：f0=0； R0=0。

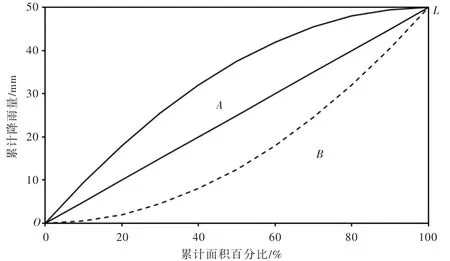
图2 降雨空间分布曲线

结合降雨空间异质性指数的定义和计算公式可知，SHIP 的范围是（-1，1），SHIP=0 表明降雨空间分布均匀，SHIP∈（-1，0）表明降雨中心位于上游，SHIP∈（0，1）表明降雨中心位于下游，且SHIP 的绝对值越大，降雨的空间分布越不均匀。因此，SHIP 可以很好地描述降雨空间分布的不均匀性。另外，降雨空间分布曲线任意两点间的斜率表示了该子区间的降雨量，因此，斜率最大的区间便是降雨中心所在位置，如图2所示，实曲线的降雨中心在最下游，而虚曲线的降雨中心在最上游。

3 洪水预警临界平面方程

中小河流洪水是否超警主要取决于某时段降雨形成的洪水是否超过河道的安全泄量，若超过，则可能引发洪水漫堤或溃堤，从而造成灾害，此时的降雨量便为预警临界雨量。有条件的地区可以通过建立洪水预报模型实现洪水的实时预报和预警，尚没有建立洪水预报方案的地区则需要借助于临界雨量进行洪水预警，根据流域的实时观测雨量，及时发布预警信息。洪水除了跟降雨量直接相关外，还受土壤含水量和降雨空间分布的影响，因此，推求的临界雨量应是随土壤含水量和降雨空间分布变化而变化的动态值。以往的动态临界雨量指标仅仅考虑了土壤含水量的影响，然而，降雨的空间分布对临界雨量指标也有较大影响，降雨中心越靠近下游，受流域的调蓄作用越小，形成的洪水就越大，相应的临界雨量指标应该越小；反之，降雨中心越靠近上游，相应的临界雨量指标应该越大。前已述及，SHIP 可以定量描述降雨空间分布的不均匀性，并能判别降雨中心的位置。因此，本文分别以洪峰前24 h 内的最大3 h 和6 h 降雨量为致灾降雨，以致灾降雨前的土壤饱和度表示土壤含水量，以降雨空间异质性指数SHIP 描述致灾降雨的空间分布，构建洪水预警指标体系，推求洪水预警的动态临界雨量指标。一般而言，构建的指标体系中，指标不宜过多，且尽量保证指标间的独立性，否则可能会赋予某一特征过多权重，而忽略了其他特性。本文选取的致灾降雨、土壤饱和度和SHIP 从成因上分析没有太大的相关性，可以认为是相互独立的指标。

在不建立洪水预报方案的前提下判断洪水是否超警，可以归为模式识别问题，即根据选定的与洪水密切相关的指标体系，判断该场次洪水的类别属性。基于统计学习理论中VC 维和结构风险最小化原则的支持向量机，通过寻求使得类间隔最大化的最优分割超平面，可以实现样本的分类。因此，可以采用支持向量机进行洪水是否超警的辨识，寻求最优分割超平面的思想具有鲜明的数学意义，将其用于洪水超警状态识别时，最优分割超平面便具有了一定的物理含义，位于最优分割超平面某一方的样本点为超警样本，位于另一方的样本点为未超警样本，则位于最优分割超平面上的样本点应为临界警戒样本点，该平面应为临界警戒平面，由此平面方程推求的雨量即为临界雨量。

根据流域上历史洪水发生情况，将实测的n 场洪水按是否超过警戒流量分为超警和未超警两类。令y=1 和y=-1 分别代表超警和未超警样本，结合构建的洪水预警指标体系，构造数据集D={（xi，yi）|i=1，2，…，n}，xi∈Rm，为输入；yi∈{-1，1}，为输出。根据支持向量机的分类原理，如果这些样本点线性可分，则存在一个最优超平面：

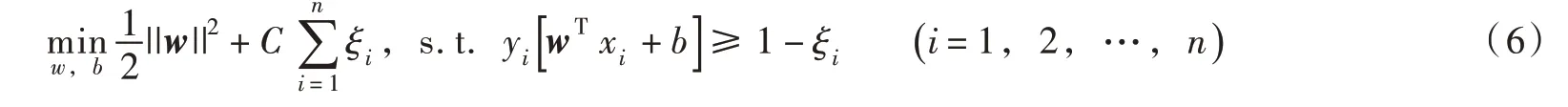
式中：C＞0 为惩罚参数，C 的引入可以使误分类点的个数尽可能少；ξi≥0 为松弛变量，ξi的引入可以降低离群点对分类模型的影响。

利用拉格朗日乘子法得到该优化问题的对偶问题，并采用序列最小优化算法（SMO）进行求解，即可得到上述最优超平面方程，该超平面方程即为临界警戒平面方程，进而可以推求不同土壤饱和度和降雨空间分布情形下的动态临界雨量指标。

4 应用研究

以汉江旬河上游为例，对上述考虑降雨空间异质性的洪水预警模型进行应用研究。旬河发源于秦岭南麓的宁陕县境内，为汉江的一级支流，流经宁陕、镇安、旬阳三县，在旬阳县城东注入汉江，全长218 km。其中，镇安县柴坪水文站以上为旬河上游，全长117 km，控制流域面积2364 km2。旬河为山溪性河流，平均比降为2.9‰，易形成陡涨陡落的大洪水，洪水灾害频繁发生。此外，旬河流域呈狭长的羽毛状，降雨的空间分布差异性较大，对洪峰的形成有较大影响。

根据《镇安县防御灾害性洪水应急预案》，镇安县境内旬河干流防御洪水对策分为3 级：当柴坪水文站洪水达到1000 m3/s 常遇洪水时，旬河干流防汛处于警戒状态；当柴坪水文站洪水达到1626 m3/s 较大灾害性洪水时，旬河干流防汛处于紧急状态；当柴坪水文站洪水达到2600 m3/s 特大灾害性洪水时，旬河干流防汛处于特别紧急状态。本文以镇安县境内的旬河干流为预警对象，根据柴坪水文站洪水是否超过1000 m3/s 进行警戒状态的预警。

旬河上游共有东江口、旬阳坝等10 个雨量站点，具体分布如图3所示。根据流域DEM 数据分析得到流域各个雨量站点的泰森多边形及其对应的面积，并利用栅格的汇流时间绘制流域等流时线，可得到7 个等流时面，如图3所示。进一步统计每个等流时面内各个泰森多边形占整个流域的面积，进而可根据式（4）得到降雨空间异质性指数SHIP 值。根据收集到的这些站点1980—2017年的雨洪摘录资料，共选取31 场洪水，计算每场洪峰发生前24 小时内最大3 h、6 h 降雨量及其对应的土壤饱和度和降雨空间异质性指数SHIP，分别构建3 h 和6 h 两种时段的包含这3 个指标的洪水预警指标体系。以1000 m3/s 作为警戒洪水，采用支持向量机模型对实测的31 场洪水进行分类模拟，3 h 和6 h 洪水预警模型的分类正确率分别达到87.10%和83.87%，如图4（a）和图5（a）所示。若仅以致灾降雨量和土壤饱和度为预警指标进行预警模式的分类，正确率只有77.42%和74.19%，分别如图4（b）和图5（b）所示。可见，考虑降雨空间分布的异质性后，洪水预警模型的精度大约可以提高10%。

图3 旬河上游雨量站点分布及等流时面划分

图4 3h 洪水预警模型分类结果

图5 6h 洪水预警模型分类结果

根据支持向量机的分类原理，通过交叉验证，最终确定惩罚参数C 为10，松弛变量ξi为0.1，经过学习训练和预测，得到各个样本的预测值。图4（a）和图5（a）中的分类平面即为临界预警平面，则该平面对应的降雨量即为临界雨量，其对应的方程分别为：

式中：Pc,3h、Pc,6h分别为3 h 和6 h 临界雨量；W 为土壤饱和度。

据此可以计算任意土壤饱和度和SHIP 组合情形下的临界雨量，表1给出了部分组合情形下的临界雨量。同等土壤饱和度条件下，如W=0，当降雨中心位于流域上游时，如SHIP=-0.4，由于受流域调蓄作用较大，需要较大的降雨才能达到洪水预警值，此时3h 临界雨量为40.89 mm，6 h 临界雨量为61.99 mm；而当降雨中心位置在流域下游时，如SHIP=0.4，由于距离流域出口较近，只需较小的降雨便可以达到洪水的预警值，此时3 h 临界雨量为30.77 mm，6 h 临界雨量为39.73 mm；若按降雨均匀分布情形下的临界雨量（3 h 为35.83 mm，6 h 为50.86 mm）进行预警，则可能会出现漏报的风险。

表1 不同土壤饱和度和SHIP 组合情形下的临界雨量 （单位：mm）

随着降雨预报的精细化发展，网格化的降雨预报产品可以更好地给出预见期内降雨的空间分布特征，借助本文提出的临界雨量推求方法，可以实现更高精度的洪水预警。实际中若无网格预报产品，暴雨空间分布尚不明确的条件下，建议降雨预见期内仍按均匀降雨进行预警（即SHIP=0），待降雨落地后，依据各雨量站观测数据求得降雨空间分布的SHIP 值后，再根据本文提出的方法进行洪水预见期内的洪水预警，逐步地提高预警的精度。

5 结论

降雨是形成洪水的直接诱因，通过临界雨量实现中小河流洪水的预警是一种可行的途径，然而洪水还受到土壤含水量和降雨空间分布等的影响，尤其是降雨的空间分布难以准确的定量描述，为洪水的高精度预警带来了困难。本文结合泰森多边形和等流时面，提出了一种反映降雨空间分布不均匀性的指标，即降雨空间异质性指数，该指标既能反映降雨空间分布不均性的程度，又能反映出降雨中心的位置，可以较全面的反映降雨的空间异质性。考虑到降雨的空间异质性对中小河流洪水预警的精度有较大影响，基于支持向量机的分类原理，将提出的指标用于洪水动态临界雨量预警指标的推求。得出的临界雨量间接考虑了流域调蓄作用的差异，更能反映洪水的真实过程，因此，采用该预警指标能实现更高精度的预警。本文提出的降雨空间异质性指数，需要流域内多个雨量站的实测或预报数据，适用于流域内降雨空间分布差异明显的地区。此外，该指数对其他需要考虑降雨空间异质性的领域，如洪水预报、干旱预警等，也有较好的应用前景。