焦炭催化CO还原NO的反应机理研究
2020-05-06许紫阳王春波刘瑞琪
许紫阳, 岳 爽, 王春波, 刘瑞琪
(华北电力大学 能源动力与机械工程学院, 河北 保定 071003)
目前,中国能源消费结构以化石燃料为主,其中,煤炭的消耗量占中国一次能源消费总量的70%左右。据统计,中国每年煤炭消耗量的50%以上都用于燃煤电站火力发电,而燃煤发电产生的大量氮氧化物NOx则是主要的大气污染物之一[1]。研究指出,大气中NOx的常见存在形态主要包括NO、NO2与N2O等,其中,NO含量占NOx总量的90%以上[2]。空气中的大量NO容易造成酸雨、光化学烟雾、平流层臭氧破坏和全球气候变暖等各种环境问题[3]。近年来,为控制燃煤电站NO的排放,燃料分级、空气分级、烟气再循环等众多低氮燃烧控制技术得到了快速发展[4],其中,燃料分级再燃技术以其效率高、费用低、易实施等优点,成为中国目前主流的低NOx燃烧技术之一[5]。
燃料分级再燃技术又称煤粉再燃技术,其基本原理是在炉内再燃区喷入煤量为10%-20%燃煤总量的再燃煤粉,使煤粉在过量空气系数小于1的条件下燃烧,从而在再燃区形成较强的还原性气氛,以此达到还原NOx的目的。由于再燃煤粉的存在,炉内再燃区内的NO还原反应可以分为均相与异相反应两种,其中,异相反应主要表现为NO与焦炭反应和焦炭催化NO与CO、H2等还原性气体发生反应两种途径[6]。Johnsson[7]在焦炭表面对NO异相还原反应机理进行了动力学实验分析。结果表明,在焦炭表面NO与CO的反应相较于NO与H2等其他气体的反应更易进行,且反应速率常数较大。对于炉内再燃区域,煤粉贫燃产生的大量CO会与主燃区产生的大量NO发生均相与异相化学反应,具有强还原性的CO气体分子与NO发生反应生成N2与CO2分子,反应方程式如式(1)所示[8,9]。
(1)
王春波等[10,11]通过对比O2/N2与O2/CO2气氛下煤粉燃烧释放NOx的不同特性,证实了还原性气体CO是降低NO释放量的重要原因。López等[12]研究了CO对异相NO还原反应的影响规律。实验结果表明,CO分子的参与能够促进焦炭表面NO还原反应的进行。上述研究不断深化了对NO还原反应的认识,但由于焦炭是一种由大量芳香环链形成的微晶多孔复杂结构组成[13],其表面上气固反应相对复杂,因此,仅采用传统实验测量手段很难对NO异相还原反应的详细机理进行深入研究。
近年来,随着计算机技术及量子理论的发展,量子化学可以从分子层面详细揭示微观反应机理。其中,密度泛函理论计算方法能够在保证计算精度的前提下优化计算成本,便于进行动力学及热力学等相关参数的计算,因此,被广泛应用于焦炭表面的化学反应机理研究[14-17]。余岳溪等[16,18]利用密度泛函理论计算方法,研究了N2O在煤焦表面的异相还原机理,得到了煤焦催化N2O异相还原生成N2的反应路径。Gao等[19]结合了密度泛函理论(DFT)与经典过渡态理论(TST),计算得到了焦炭催化N2O异相反应的反应机理及动力学参数,结果表明,焦炭作为催化剂可显著降低异相N2O还原反应的反应能垒。除此之外,含氮煤焦表面还原NOx的反应机理也被详细研究,Jiao等[20,21]计算得到了NO被含氮焦炭还原的反应路径,并且发现吸附在焦炭表面的CO分子可显著降低剩余氧解吸阶段的能垒,从而提高反应速率。
综上可知,目前对于焦炭催化NOx还原反应的DFT研究报道主要集中于N2O异相还原及含氮焦炭还原NO的反应机理,而针对煤粉再燃过程中CO还原NO的反应机理研究报道较少。因此,本研究采用密度泛函理论计算方法,对均相以及异相CO还原NO的反应机理进行分子层面理论计算,对异相机理的研究采用Zigzag与Armchair两种焦炭模型。优化得到各反应路径上所有驻点的几何构型及能量,并从能量变化与动力学角度分析比较了均相以及两种异相反应路径下的反应特性,为深入研究煤粉再燃过程中低NOx控制机理提供一定的理论指导依据。
1 实验部分
1.1 模型选择
研究表明,焦炭主要是由12-25个碳原子簇构成的大型芳香族环型结构组成[22],其中,锯齿(Zigzag)型和扶手(Armchair)型的焦炭表面因具有较强的反应活性,常被用于焦炭反应机理研究[23-25]。余岳溪等[16]采用Armchair模型,成功揭示了煤焦异相还原N2O的反应机理;张秀霞等[13,14]使用Zigzag模型,完善了N2O在异相生成及还原的反应理论。Espinal等[26]同时研究了H在Zigzag与Armchair两种焦炭结构上反应生成碳氢化合物的反应机理,经实验验证,其计算结果与实验结果吻合良好。综上,本研究选取Armchair与Zigzag两种焦炭表面作为计算模型,结构见图1。
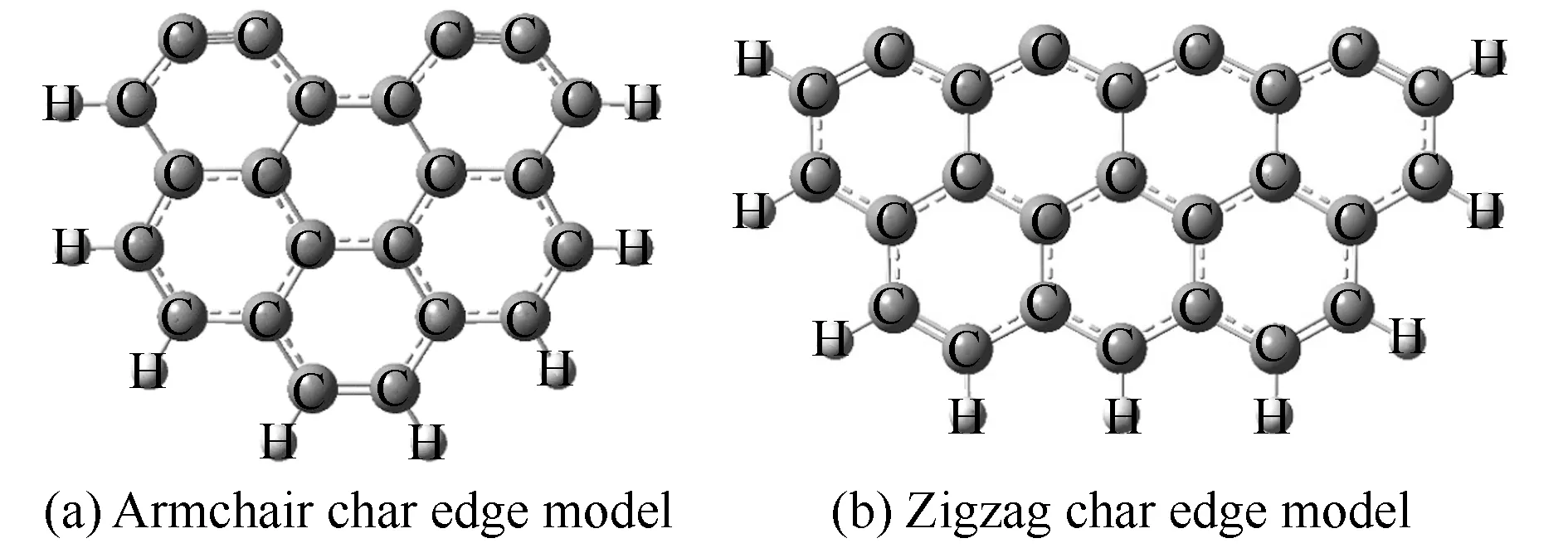
图1 焦炭表面模型结构示意图
1.2 计算方法
本研究中的结构优化计算采用密度泛函理论中的B3LYP方法和Def 2-SVP基组联用,能量计算及振动频率分析采用双杂化泛函理论中的B2PLYP方法和def 2-TZVP基组联用[27],能量计算均考虑了零点能校正。根据几何优化计算,分别得到不同反应路径中的反应物(P)、产物(R)、各中间体(IM)及过渡态(TS)的几何构型,并通过振动分析和内禀坐标计算(IRC)确定所得过渡态的合理性,保证各过渡态结构与反应物、中间体和产物之间的正确连接[21]。本研究计算程序均为Gaussian16[28]。
采用经典过渡态理论(TST)可以得到各反应动力学参数,计算公式如下[29]:
(2)
(3)
式中,Γ为量子隧道修正系数;Ea为反应能垒,kJ/mol;R为气体摩尔常数,J/(mol·K);T为温度,K;kB为玻尔兹曼常数,J/k;h为普拉克常数,J·s;QTS、QA和QB依次为过渡态TS、反应物A和反应物B的配分函数;vm为反应路径振动的频率;cm-1;c为光速,单位为m/s。
2 结果与讨论
2.1 均相反应
均相NO-CO反应的反应过程与能量变化见图2,反应中涉及的各驻点结构见图3。需要注意的是,反应路径中每一阶段内各驻点的能量均为相对于此阶段内反应物能量的能量之差。
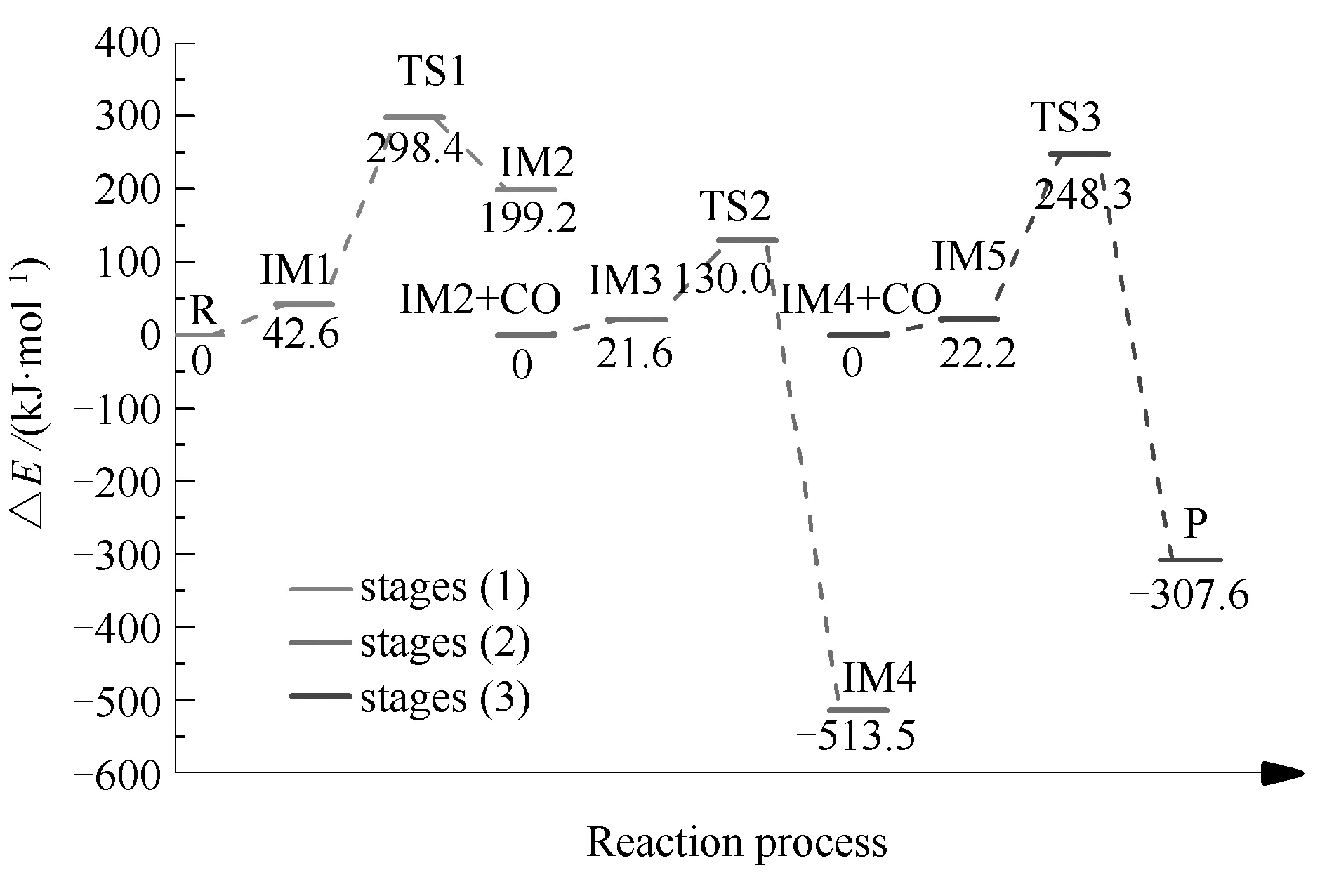
图2 均相NO-CO反应的能量变化
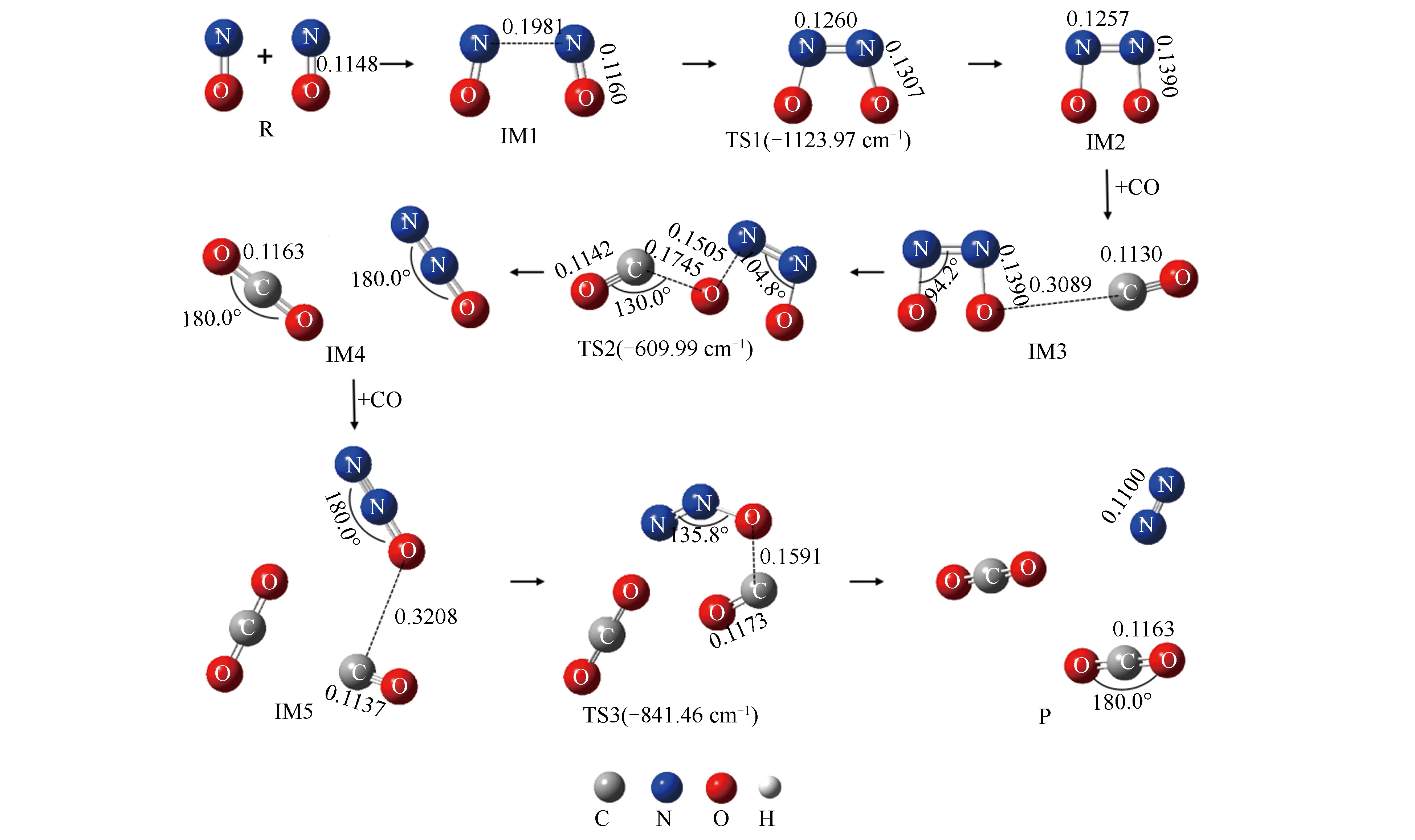
图3 均相NO-CO反应的各驻点结构示意图
结合图2和图3可知,均相NO-CO反应经历了三个过渡态和五个中间体,最终反应生成一个N2分子和两个CO2分子。根据反应过程中分子数量的变化,可以将整个反应分为三个基元反应阶段,即NO二聚体形成、N2O形成与N2形成阶段。各阶段反应过程分别为:第一阶段自由气体状态下的两个NO分子相互靠近逐渐形成IM1,随后克服255.8 kJ/mol的反应能垒形成NO二聚体。此过程中N-N键键长变化为∞(R)→0.1981 nm(IM1)→0.1260 nm(TS1)→ 0.1257 nm(IM2);同时NO分子的N-O键由0.1148 nm被拉长至0.1390 nm,逐渐趋向于断裂;第二阶段游离的CO分子攻击IM2中的一个O原子,C原子与O原子间距离由0.3089 nm缩短至0.1745 nm;同时IM2中N-O键发生断裂,键长由0.1390 nm伸长至0.1505 nm。最终反应经过渡态TS2形成一个CO2分子和一个N2O分子,此阶段的反应能垒为108.4 kJ/mol;第三阶段另一个游离的CO分子克服226.1 kJ/mol的能垒夺走N2O中的一个O原子,反应最终生成一个N2分子和两个CO2分子。
由均相NO-CO反应的能量变化可以发现,反应过程中的第一阶段,即NO二聚体的形成过程能垒最高,这说明在此均相反应中由IM1到IM2的基元反应是整个反应的决速步。此外,通过对比N2O形成与N2形成阶段的反应过程可以看到,N2O形成阶段能垒较低,这表明,在均相NO-CO反应中,NO二聚体(IM2)比N2O分子更容易与CO发生反应。
2.2 焦炭催化异相反应
在焦炭表面进行的异相反应均以化学或物理吸附作为反应的第一步。对于本研究焦炭表面CO还原NO的异相化学反应,NO在焦炭表面的吸附是整个还原反应的第一步。研究指出[18],NO在焦炭表面吸附可分为O-down、N-down与Side-on三种方式,其中,O-down与N-down吸附方式表现为NO分子中的O原子与N原子分别单独吸附在焦炭表面活性位点,而Side-on吸附方式则表现为NO分子水平吸附在焦炭表面上两个活性位点。Kyotani等[30]的研究表明,相较于其他两种吸附方式,NO主要以Side-on方式吸附于焦炭表面。因此,本研究在对异相反应的机理研究中,均采用NO以Side-on方式吸附在Zigzag与Armchair焦炭表面上的构型作为起始反应物,优化后的NO吸附结构如图4所示,并给出了吸附在焦炭表面的N-O键键长。同时为便于描述,对焦炭模型中所有参与反应的原子进行了编号。
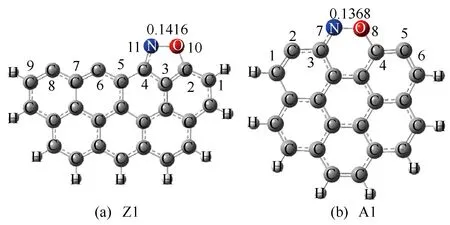
图4 起始反应物结构
由图4可知,吸附在Zigzag与Armchair型焦炭表面上的NO分子,其N-O键的长度分别为0.1416和0.1368 nm;而自由气体状态下的NO分子,其N-O键的长度仅为0.1100 nm。可以看到,NO分子吸附在焦炭表面后其N-O键明显被拉长,N、O原子趋向于分离,说明焦炭能够促进NO分子的裂解,从而加快还原反应的进行。
2.2.1 Zigzag型焦炭催化异相反应(路径1)
Zigzag型焦炭催化异相NO-CO反应的过程与能量变化见图5,反应中涉及的各驻点结构见图6。为便于描述,将该反应路径称为路径1。
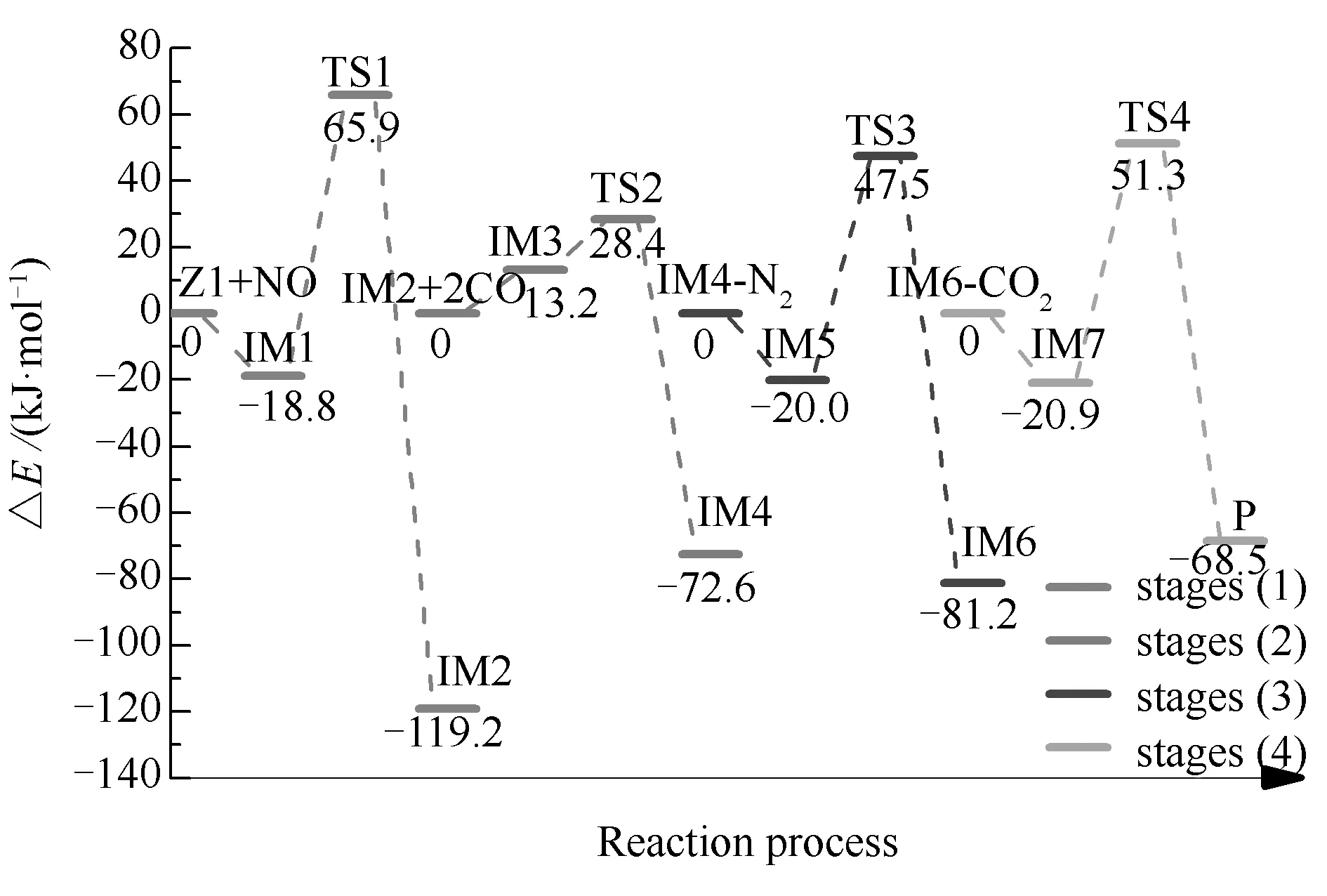
图5 Zigzag型焦炭催化异相NO-CO反应的能量变化
结合图5与图6可以看到,反应路径1经历了四个过渡态和七个中间体,最终反应生成一个N2分子和两个CO2分子。与均相反应类似,根据反应过程中反应分子数量的不同,将反应路径1分为四个反应阶段,分别为N2形成、N2释放以及两步CO2释放阶段,其中,前两个阶段为NO异相还原过程,后两个阶段为CO2脱附过程。各阶段反应过程描述如下:(1)首先,游离的NO分子以O-down形式吸附在起始反应物Z1上形成稳定中间体IM1,N-O键长由0.1100 nm被拉长为0.1323 nm,已经趋向于分离。随后,IM1中两个N原子相互靠近并克服84.7 kJ/mol的反应能垒形成N2分子,此过程中N-N(11)键键长变化为:0.3439 nm(IM1)→0.1994 nm(TS1)→0.1283 nm(IM2);(2)两个游离的CO分子首先吸附在IM2中两个自由O原子上形成IM3;随后N2分子经过渡态TS2从焦炭表面脱离,C(4)-N(11)键长由0.1423 nm拉伸至0.3860 nm。在脱离过程中N2分子的N-N键的长度由0.1190 nm(IM3)缩短至0.1100 nm(IM4),最终与自由气相状态下N2分子的N-N键键长一致,从而实现N2从焦炭表面的完全脱附。此阶段的反应能垒仅为15.2 kJ/mol;(3)吸附在C(6)位点上的CO2分子经过67.5 kJ/mol的反应能垒后从焦炭表面脱离,C(6)-O键键长变化为:0.1403 nm(IM5)→0.1810 nm(TS3)→0.3368 nm(IM6);与此同时,CO2分子的C-O-C键角由130.7°增大至180°;(4)与阶段(3)类似,吸附在C(2)位点上的CO2分子克服72.2 kJ/mol的反应能垒脱离焦炭表面,C(2)-O键长由0.1404 nm增长至0.3314 nm,CO2分子的C-O-C键角由132.2°增大至180.0°。
根据反应路径1中NO异相还原过程即阶段(1)与阶段(2)的能量变化可知,阶段(1)的反应能垒较高。这说明在Zigzag表面的NO异相还原反应过程中,阶段(1)即IM1→IM2的反应是此NO异相还原过程的决速步。与均相NO还原反应决速步的能垒相比,路径1中NO异相还原反应的能垒更低,表明Zigzag型焦炭催化下的NO异相还原反应较均相反应更容易发生。
2.2.2 Armchair型焦炭催化异相反应(路径2)
Armchair型焦炭催化异相NO-CO的反应过程与能量变化见图7,反应中涉及的各驻点结构见图8,为便于描述,将该反应路径称为路径2。
结合图7与图8可以看到,反应路径2经历了N2形成、N2释放及两步CO2释放四个阶段。反应经历八个中间体和五个过渡态,最终生成了一个N2分子及两个CO2分子。同样地,在反应路径2中前两个阶段为NO异相还原过程,后两个阶段为CO2脱附过程。各阶段的反应过程详情如下:(1)游离的NO分子以O-down形式吸附在A1表面形成IM1,随后两个N原子相互靠近并经过48.1 kJ/mol的反应能垒形成N2分子;N-N键长由0.2773 nm(IM1)缩短至0.1238 nm(IM2)。随后此N2分子发生旋转经过渡态TS2形成IM3;(2)游离的两个CO分子首先吸附在IM3中两个自由O位点上形成IM4,随后N2分子仅经过20.5 kJ/mol的反应能垒脱离焦炭表面。脱离过程中C(3)-N(7)键长由0.1439 nm伸长至0.3146 nm,同时N2分子的N-N键长由0.1187 nm(IM4)缩短至0.1100 nm(IM5);(3)IM6中C(4)位点上的CO2分子经过80.9 kJ/mol的反应能垒脱离焦炭表面,C(4)-O键长由0.1405 nm(IM6)增长至0.4000 nm(IM7),同时CO2分子的键角由132.1°(IM6)增大至180°(IM7);(4)IM8中C(2)位点上的CO2分子经过74.5 kJ/mol的反应能垒从焦炭表面脱离,C(2)-O键长由0.1404 nm增长至0.3857 nm,同时CO2分子键角由132.1°(IM8)增大至180.0°(P)。
根据路径2中NO异相还原过程即阶段(1)与阶段(2)的能量变化可知,阶段(1)即IM1→IM2的反应是路径2中NO还原反应过程的决速步。与路径1中NO还原过程的决速步相比,路径2中NO还原反应过程的决速步能垒更低,这表明与Zigzag型焦炭相比,在Armchair型焦炭表面进行的异相NO还原反应更容易发生。同时,与均相NO还原反应的决速步能垒相比,路径1和路径2中的异相NO还原反应过程决速步能垒均更低,这进一步表明了异相NO还原反应较均相NO还原反应更容易发生。
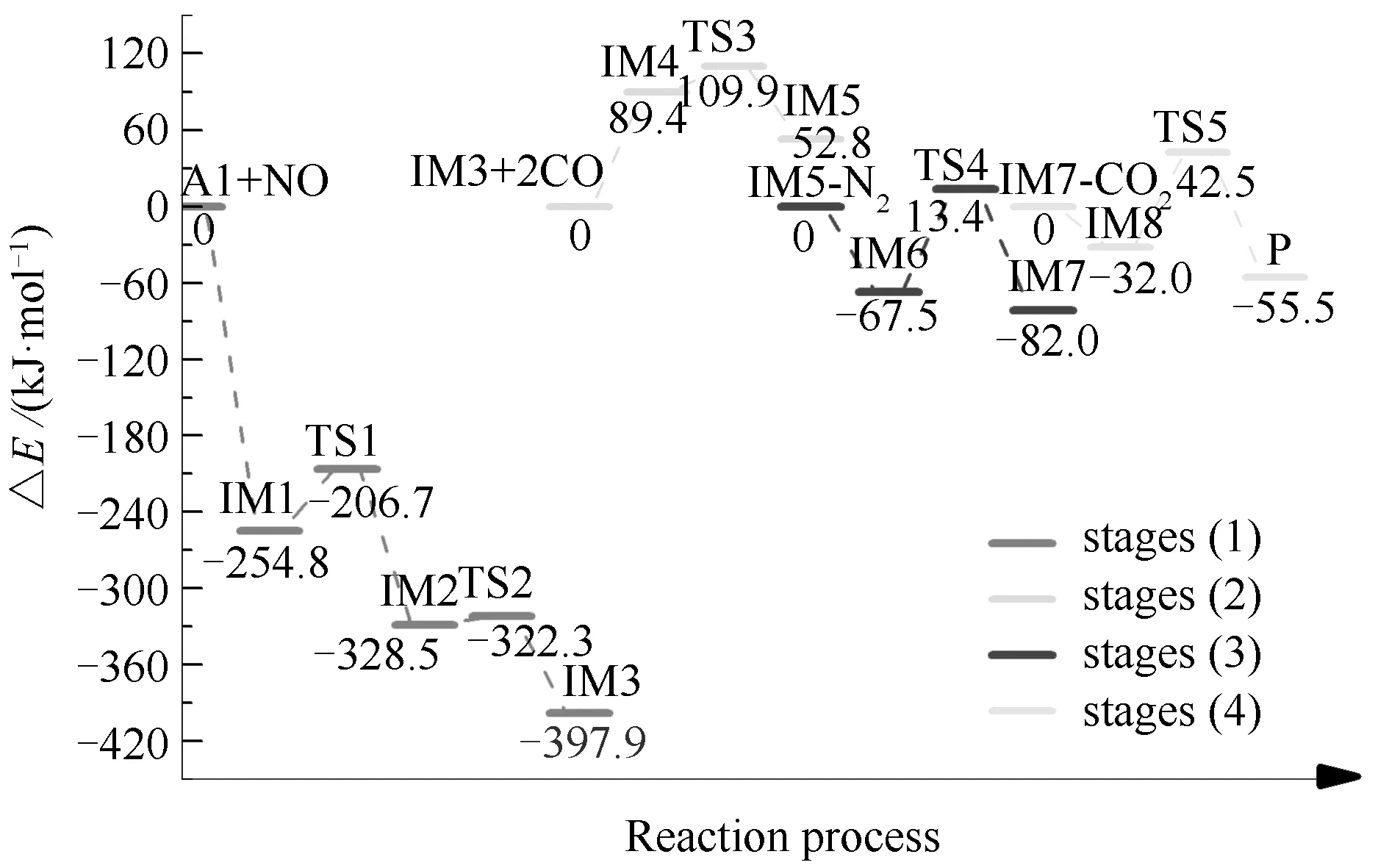
图7 Armchair型焦炭催化异相NO-CO反应的能量变化
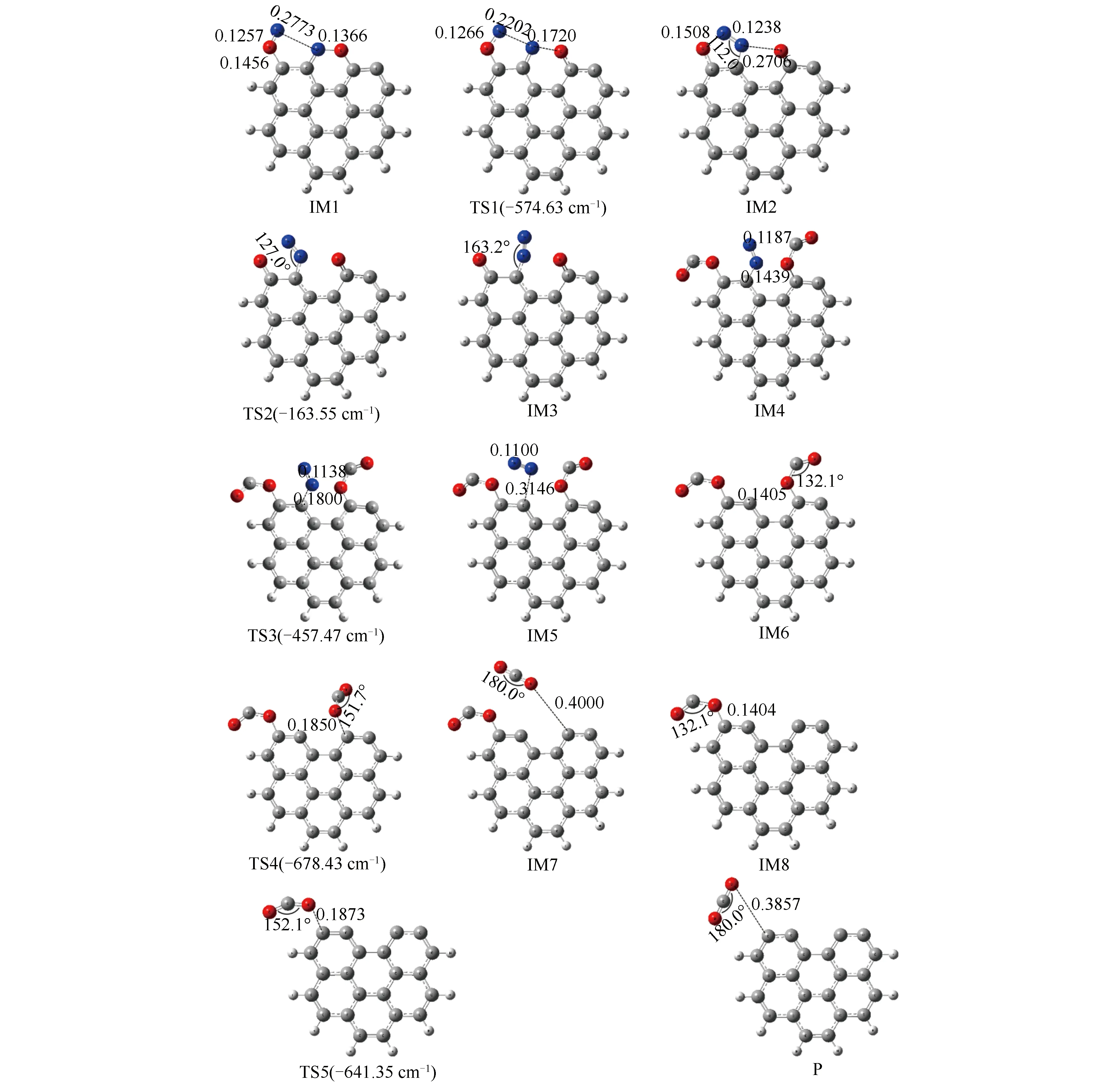
图8 Armchair型焦炭表面反应各驻点结构
此外,对比路径1与路径2的CO2脱附过程的能量变化可以看出,路径2中两个CO2分子脱附过程即阶段(3)与阶段(4)的反应能垒均高于路径1各对应阶段,这表明,CO2分子的脱附在Zigzag型焦炭表面更容易发生。从以上分析可以看出,不同路径中相同反应阶段的能垒值存在差异,说明不同焦炭模型对反应特性存在较大影响,理论计算应充分考虑焦炭模型的选用对计算结果的影响。
2.3 反应动力学分析
动力学分析可以衡量化学反应的快慢程度,为建立预测模型提供必要反应动力学参数。根据经典过渡态理论,计算均相与焦炭异相催化作用下三种不同反应路径NO还原反应过程的决速步在400-1600 K的反应速率常数,结果如图9所示。同时对图9所得曲线计算结果进行拟合,得到各反应路径的动力学参数,结果见表1。
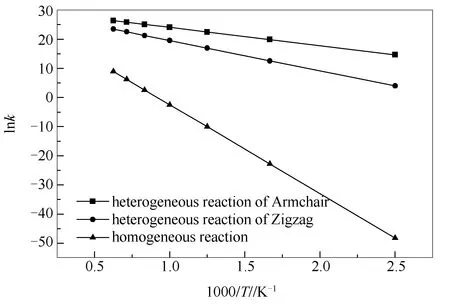
图9 不同温度下各反应的反应速率常数

表1 反应动力学参数
由图9可知,随着温度的上升,各反应路径的速率常数均增大,该趋势同文献中各实验结论一致[8-10],说明提高温度对NO还原反应起到促进作用。在所选温度范围内,异相反应的速率常数均大于同温度下的均相反应的速率常数;并且在异相反应中,Armchair型焦炭表面NO还原反应的速率常数大于同温度下Zigzag型焦炭表面NO还原反应的速率常数。此外可以看出,在低温下,均相反应的速率常数明显小于异相反应的速率常数,因此,可以认为,在同时存在均相与异相反应的条件时,均相反应几乎不发生;随着温度的上升,与异相反应相比,均相反应的反应速率上升更快,这说明均相NO还原反应受温度的影响更大。
由表1可知,与均相反应相比,异相NO还原反应的活化能更低且指前因子更大,这表明异相反应更易发生;并且Armchair型表面的NO异相还原反应活化能较Zigzag型更低,表明NO异相还原反应在Armchair型焦炭表面上更容易进行。综上所述,在CO还原NO的反应中,焦炭能够降低反应的活化能并且加快反应速率,起到了催化反应进行的作用。
3 结 论
本研究基于量子化学密度泛函理论对均相以及焦炭催化异相CO还原NO的反应机理进行了研究。计算结果表明,均相NO还原反应的活化能为254.06 kJ/mol;Zigzag型焦炭催化异相NO还原的反应活化能为86.94 kJ/mol;Armchair型焦炭催化异相NO还原反应的活化能为52.16 kJ/mol。异相反应的活化能均小于均相反应,说明焦炭在CO还原NO的反应中起到了催化作用。
焦炭表面CO还原NO的反应历经N2形成、N2释放及两步CO2释放四个阶段,最终形成一个N2分子与两个CO2分子。其中,Zigzag型与Armchair型焦炭表面进行的NO异相还原反应的决速步均为N2形成阶段。
不同焦炭模型对异相NO还原反应特性有较大影响;在焦炭表面进行的NO异相还原反应路径中,与Zigzag型焦炭相比,Armchair型焦炭表面的NO还原反应的决速步能垒更低且反应速率更快,表明NO还原反应在Armchair型焦炭表面上更容易进行。
