基于价格和服务竞争的传统零售商与电子零售商信息分享问题研究

赵 静，李影婕，王秀兰

(天津工业大学 数学科学学院，天津 300387)

电子商务的迅速发展，催生了大量电子零售商，他们通过网络在线渠道向消费者销售产品，如京东商城、苏宁易购等。电子零售商的出现给传统零售商(通过实体店销售产品的零售商)带来了巨大的竞争压力[1]。低层次的价格战已不再满足市场竞争的需要，为提高消费者满意度进而增加产品销量和企业利润，传统零售商与电子零售商纷纷向消费者提供服务。比如，京东商城等电子零售商向消费者提供在线客服咨询、商品比价、物流配送等服务；沃尔玛等传统零售商向消费者提供导购互动服务、产品定期更新、立即退换货等服务。传统零售商与电子零售商之间不仅存在价格竞争，而且存在服务竞争。

由于社会环境的复杂多变，市场需求存在较大的不确定性。随着信息技术的发展，电子零售商可以在线实时获取网购消费者的消费数据，传统零售商也可以通过POS系统等获取实体店产品的消费数据，他们都可以通过数据挖掘等技术获得比以往更为精准的市场需求预测信息。供应链成员间需求信息分享逐渐变得普遍(Zhou和Benton，2007[2]；Zhang和Chen，2013[3]；Huo等2014[4])，以往文献研究表明需求信息分享能够带来一些好处，比如保持供需平衡、减轻牛鞭效应和减少成本支出等[5-6]。但需求信息分享并非总是有利的，如Gal-Or(1985)[7]研究表明，在Cournot竞争中不分享信息比分享信息时公司所获得的利润更高。由于价格和服务的双重竞争，传统零售商与电子零售商之间的需求信息分享问题变得更为复杂。

传统零售商与电子零售商之间需求信息分享如何影响其价格、服务决策以及最大期望利润？在价格和服务竞争共存的情形下，传统零售商与电子零售商何时自愿分享需求信息？何时可通过信息分享激励两零售商分享需求信息？信息精度对最优定价和最优服务策略有何影响？价格和服务竞争对信息分享策略有何影响？这些问题都是传统零售商与电子零售商决策者迫切需要解决的管理问题。

针对以上问题，本文建立了传统零售商和电子零售商需求信息分享与不分享两种情况下的定价与服务决策模型，对最优定价、服务水平以及最大期望利润进行比较分析，并通过数值算例分析了主要参数对两零售商信息分享期望值的影响。

以往文献中，关于同一水平零售商之间进行需求信息分享的问题已有一些研究成果。如Vives(1984)[8]研究了销售替代品的两寡头公司Nash博弈情形下的需求信息分享激励问题，结果表明信息分享比不分享时获得更高利润。在此基础上，Gal-Or(1985)[7]研究了销售同一类产品的N家公司的水平信息分享问题，结果表明信息不分享是唯一的Nash均衡。Li等(2014)[9]和Yan等(2015)[10]研究的是销售替代品的两公司之间的需求信息分享问题，前者表明在Nash博弈中预测的需求信息不完全相关时，两公司都会从信息分享中受益；后者发现两公司在Stackelberg博弈中的利润总是高于Nash博弈的利润。Yue等(2006)[11]和Mukhopadhyay等(2011)[12]分别研究了销售互补品的两公司在Nash博弈和Stackelberg博弈下的需求信息分享问题，结果表明在Nash博弈下，信息分享是否对两公司及整个供应链有利依赖于模型中的参数取值；而在Stackelberg博弈下信息分享对博弈领导者是有益的，但是对博弈跟随者及整个供应链是不利的。以上文献都是基于无差异的两(多)个传统零售商定价决策，对需求信息分享问题展开研究的。与上述文献不同的是，本文基于现实背景考虑了传统零售商和电子零售商市场份额的差异，在他们之间存在价格和服务竞争的前提下对信息分享问题进行了探讨。

另外，少量研究考虑了零售商的定价和服务决策问题。如Tasy和Agrawal(2000)[13]讨论了两个传统零售商在非合作与合作时的最优定价和服务决策问题。丁锋和霍佳震(2014)[14]研究了服务水平对非合作与合作情境下的传统零售商和电子零售商定价和需求的影响。张盼等(2012)[15]研究了只有传统零售商提供服务情况下网络渠道的开通对传统零售商最优定价、服务水平及其最大利润的影响。以上文献均是在需求确定的环境下展开研究的，本文则考虑了需求的不确定性，并且对传统零售商和电子零售商需求预测信息分享问题进行了探讨。

一、问题描述及假设

考虑传统零售商和电子零售商向消费者销售替代品，传统零售商向消费者提供服务水平为s1、价格为p1的产品，电子零售商向消费者提供服务水平为s2、价格为p2的产品。

参考Vives(1984)[8]，假设传统零售商和电子零售商的线性需求函数分别为

q1=θa-αp1+βp2+λ1s1-λ2s2

(1)

q2=(1-θ)a-αp2+βp1+λ1s2-λ2s1

(2)

式中：a为产品的市场基础；θ(0<θ<1)为传统零售商所占的市场份额，θ越大表示在传统零售商购买产品的消费者越多，1-θ则代表电子零售商所占的市场份额；非负参数α为产品需求对自身价格的敏感系数；非负参数β为交叉价格敏感系数，表示两产品价格竞争程度，β越大说明两产品价格竞争越激烈。假设α>β，即产品需求的自身价格敏感程度大于交叉价格敏感程度。非负参数λ1、λ2分别为产品需求对自身服务水平和交叉服务水平的敏感系数，λ2越大说明两零售商的服务竞争越激烈。假设λ1>λ2，即产品需求的自身服务水平敏感程度大于交叉服务敏感程度。

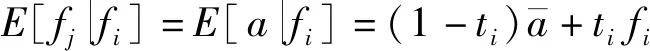
(3)

(4)

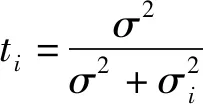
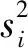
根据以上假设，传统零售商和电子零售商的利润函数分别表示为

π1(p1，s1)=p1(θa-αp1+βp2+λ1s1-

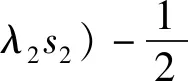
(5)

π2(p2，s2)=p2[(1-θ)a-αp2+βp1+

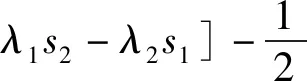
(6)

二、模型建立及求解

考虑传统零售商和电子零售商拥有相当的市场权力，现实中传统大型超市家乐福与大型电商京东商城等都属于此情形。他们之间进行Nash博弈，同时决策各自的定价与服务水平。以下分别考虑传统零售商和电子零售商不分享与分享需求预测信息的情形。

1. 传统零售商与电子零售商不分享预测信息

考虑传统零售商和电子零售商不分享彼此的需求预测信息，他们在各自的预测信息下最大化期望利润。传统零售商和电子零售商的期望利润函数分别为

E[π1(p1，s1)|f1]=p1(θE[a|f1]-αp1+βp2+

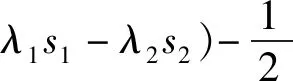
(7)

E[π2(p2，s2)|f2]=p2[(1-θ)E[a|f2]-αp2+

(8)

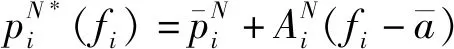
证明参考Vives(1984)[8]和Basar(1974)[21]的研究结果，易知最优定价和最优服务水平都是预测信息的线性形式，假设为

根据式(7)，期望利润函数E[π1(p1，s1)|f1]关于p1和s1的一阶和二阶偏导数分别为

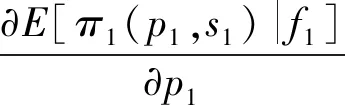
λ1s1-λ2s2

(9)

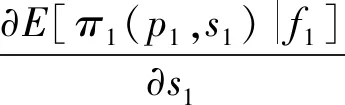
(10)

(11)

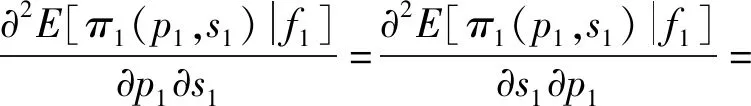
(12)

由式(11)、(12)得Hessian矩阵

(13)

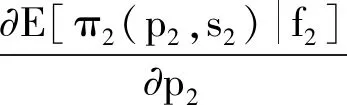
βp1+λ1s2-λ2s1

(14)

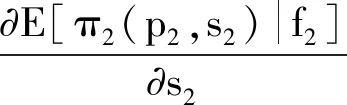
(15)

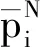
将得到的最优定价和最优服务水平策略分别代入式(5)、(6)中，取期望，即可得到传统零售商和电子零售商的最大期望利润。证毕。

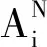
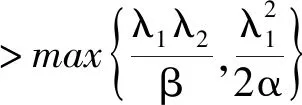
由命题1可知，两零售商不分享信息时，当服务成本系数达到一定阈值(与θ无关)时，预测信息对最优定价和最优服务水平的影响总是随着自身信息精度增加而增大。这与文献Vives(1984)[8]只考虑价格竞争的信息分享问题的研究结果有所不同，它的研究结论表明，随着信息精度的增加，预测信息对最优定价的影响总是增大的。

2. 传统零售商与电子零售商分享预测信息

考虑传统零售商和电子零售商分享彼此的需求预测信息的情形，此时两零售商在双方的预测信息下最大化其期望利润，期望利润函数分别为

E[π1(p1，s1)|f1，f2]=p1(θE[a|f1，f2]-αp1+

βp2+λ1s1-λ2s2)-

(16)

E[π2(p2，s2)|f1，f2]=p2[(1-θ)E[a|f1，f2]-

αp2+βp1+λ1s2-λ2s1]-

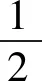
(17)

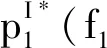
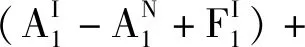
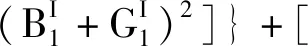
(18)

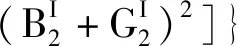
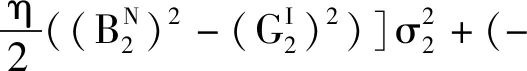
(19)

证明方法同定理1。

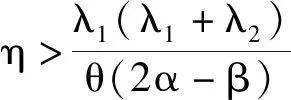
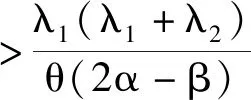
由命题2可知，两零售商信息分享时，服务成本系数在特定范围内，自身预测信息精度的增加，增强了其预测信息对最优定价和最优服务水平的影响；而对方预测信息精度的增加，降低了其预测信息最优定价和最优服务水平的影响。

3. 比较分析

对两零售商分享信息与不分享信息两种情形下的最优定价、最优服务水平和最大期望利润进行比较分析，得到命题3。

证明对定理1、2中的最优定价与最优服务策略做差，整理易得。证毕。

信息分享期望值式(18)、(19)分别表示传统零售商与电子零售商信息分享时增加的那部分期望利润。由于式(18)、(19)形式比较复杂，故参考文献Yue等(2006)[11]的分析方法进行了如下分析。

条件1：式(18)>0，式(19)>0。

条件2：式(18)、(19)有且只有一个小于零，但总的信息分享期望值V=V1+V2>0。

条件3：式(18)<0，式(19)<0。

分析以上条件，可得到如下结果：(1)若参数取值满足条件1，传统零售商与电子零售商分享需求信息后的期望利润大于不分享信息的期望利润，则信息分享对两零售商都是有利的，他们自愿分享需求预测信息，并采取定理2中分享需求信息的最优定价、服务水平策略；(2)若满足条件2，一个零售商分享需求信息后期望利润增加，另一个零售商分享信息后期望利润减少，但总的信息分享期望值增加。为激励两零售商分享信息，可设计信息分享合同，指导信息分享期望值为正的零售商将一部分期望利润补偿给信息分享期望值为负的零售商；(3)参数取值若满足条件3，两零售商的信息分享期望值均为负，信息分享对他们都是不利的，此时两零售商采取定理1中不分享需求信息的最优策略。

基于以上分析，命题4给出了传统零售商和电子零售商采取信息分享策略的充要条件。

命题4传统零售商和电子零售商采取信息分享策略，当且仅当满足下列条件之一：

(i) 式(18)≥0，式(19)≥0；

(ii) 总的信息分享期望值非负，并存在信息分享合同以分割收益。

三、数值分析

通过数值分析研究模型中主要参数的变化对传统零售商、电子零售商及总的信息分享期望值的影响，以期得到有价值的管理启示。

选取多组参数取值进行计算分析，发现其影响趋势是一致的，限于篇幅只列出一组参数的结果。以下分析中参数取值为：θ=0.7(0-1)，α=2，β=1.3(1-2)，λ1=1，λ2=0.9(0-1)，η=0.7(0.7-5)，σ1=20(0-60)，σ2=20，σ=40(0-60)，括号中的数值代表参数为变量时的取值范围。

图1～6分别给出了传统零售商市场份额θ、交叉价格敏感系数β、交叉服务敏感系数λ2、服务成本系数η、市场需求标准差σ以及传统零售商预测信息标准差(1)电子零售商预测信息标准差σ2对传统零售商、电子零售商及总的信息分享期望值的影响的分析与传统零售商预测信息标准差对其影响的分析是相似的，本文不再赘述。σ1对传统零售商、电子零售商及总的信息分享期望值的影响。

(1) 从图1可以看出：传统零售商信息分享期望值随着传统零售商市场份额θ的增加而增加，而电子零售商信息分享期望值随着传统零售商市场份额θ的增加而减少。当传统零售商和电子零售商的市场份额相同时，其信息分享期望值也相同，此时总的信息分享期望值最小；两零售商市场份额差别越大，总的信息分享期望值越大，越有利于信息分享策略的实施。

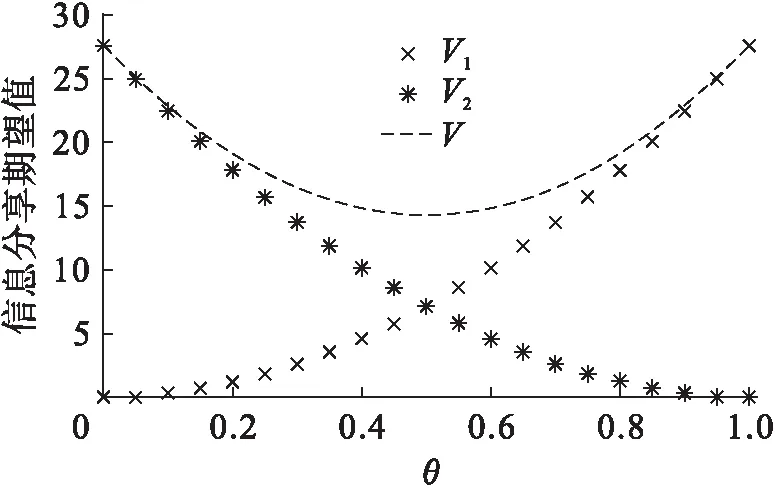
图1 传统零售商市场份额θ的影响

(2) 图2显示，两零售商及总的信息分享期望值随着交叉价格敏感系数β的增大而增加。这也表明，两产品价格竞争越激烈越有利于两零售商的信息分享。这与Yan和Pei(2015)[10]只考虑价格竞争的信息分享问题的研究结果一致。

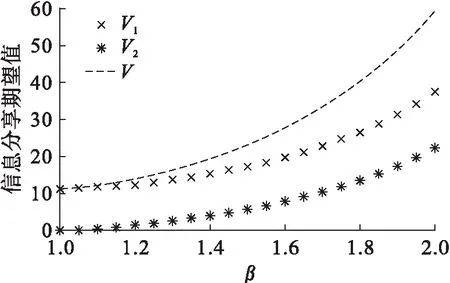
图2 交叉价格敏感系数β的影响

(3) 图3显示，两零售商及总的信息分享期望值随着交叉服务敏感系数λ2的增大而减小。交叉服务敏感系数越大，意味着两零售商服务竞争越激烈，这不利于两零售商信息分享策略的实施。

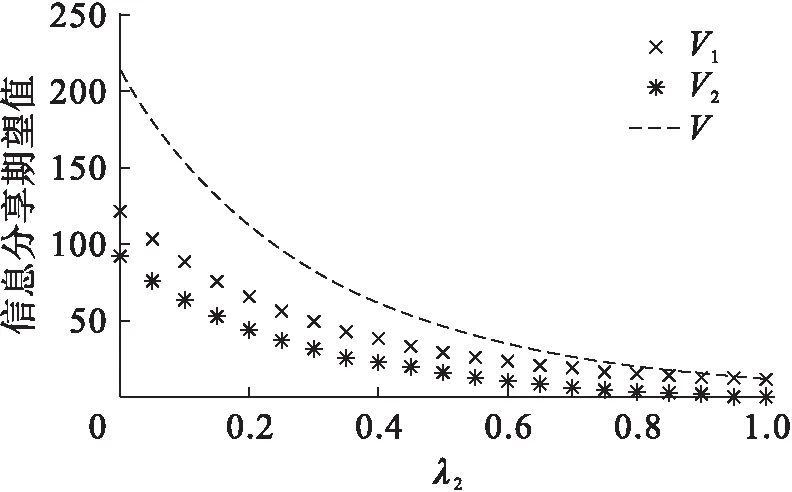
图3 交叉服务敏感系数λ2的影响

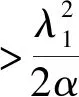
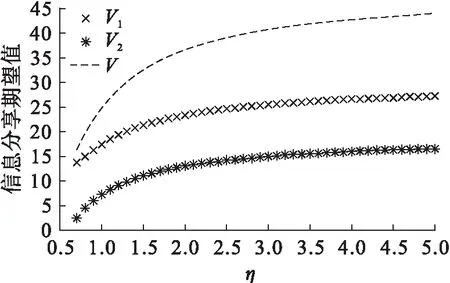
图4 服务成本系数η的影响

(5) 从图5中可以看出，两零售商及总的信息分享期望值随着市场需求标准差σ的增加而增加。市场需求标准差越大代表市场需求波动越大。传统零售商和电子零售商的信息分享期望值都随着市场需求不确定程度增加而增加。

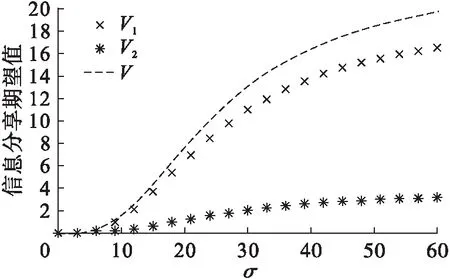
图5 市场需求标准差σ的影响

(6) 从图6可看出，传统零售商以及总的信息分享期望值随着预测信息标准差σ1的增大而增加，而电子零售商的信息分享期望值随着传统零售商预测信息标准差σ1的增大而减小。

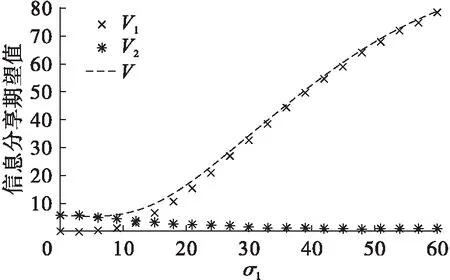
图6 传统零售商预测信息标准差σ1的影响

图6中传统零售商预测信息标准差增加意味着其预测信息精度降低，通过信息分享，传统零售商的信息分享期望值为正值，即增加了其期望利润；而电子零售商的信息分享期望值为负值，意味着信息分享减少了电子零售商的期望利润。总的信息分享期望值为正值，此时符合条件2，可以设计信息分享合同，将传统零售商的一部分利润补偿给电子零售商，从而激励两零售商信息分享。结论(5)、(6)与文献Yue等(2006)[11]研究销售互补品的两公司定价决策下的信息分享问题的结果一致：当市场需求波动较大时，信息分享会使两公司都受益；预测信息精度低的公司能从信息分享中获得更多收益。

四、结 语

社会经济的迅速发展使得传统零售商与电子零售商的竞争不仅表现在价格层面上，还延伸到服务层面上，两零售商如何在价格和服务竞争下采取需求信息分享策略以获得更大收益是本文研究的主要问题。为此，本文建立了两零售商信息分享与不分享两种情形下关于定价和服务决策的Nash博弈模型，得到了相应的最优解。比较分析信息分享与不分享时的最优均衡解，结果表明只在某些条件下信息分享后的最优定价、服务水平以及最大期望利润比信息分享前的高；当服务成本系数处在一定范围时，自身信息精度越高，对方信息精度越低，其预测信息对最优定价和最优服务水平的影响越大。数值分析表明，两零售商的市场份额差别越大、价格竞争越激烈、服务竞争程度越小及市场需求波动越大，则两零售商预测信息精度差别越大，越有利于两零售商自愿采取信息分享策略或实施信息分享激励合同。

本文基于价格和服务的双重竞争研究了传统零售商与电子零售商之间需求信息分享的问题，丰富了供应链中同水平企业信息分享问题的理论研究，也为传统零售商与电子零售商面对价格和服务竞争时进行需求信息分享策略选择提供了理论依据和参考价值。本文只考虑了两零售商拥有相当市场权力的情况，不对称市场权力的情况是进一步的研究课题。另外，本文仅考虑了两零售商需求信息分享的情况，考虑产品增值服务成本信息的分享也是今后值得研究的课题。