具有老化效应或学习效应的最大化费用节省的双代理排序博弈
2020-05-06王小丽
刘 鹏,王 赛,王小丽
(沈阳工业大学 管理学院,沈阳 110870)
工件的加工时间与该工件在加工序列中的实际加工位置有关,这种现象被称为“老化效应”或“学习效应”。老化效应即工件的实际加工时间与工件的实际加工位置呈递增的变化趋势,而学习效应则与之相反,工件的实际加工时间与工件的实际加工位置呈递减的变化趋势。在现实加工过程中,往往存在一个代理不能单独完成一个项目,而需要两个代理合作才能完成的情况。每个代理都有一台机器可用于加工这个项目里的所有工件,需要找到这批工件的一个合理的划分,以找到这两个代理加工工件总费用节省的最大值。
一、文献综述
工件加工时间与位置相关的排序问题近年来越来越多地受到普遍关注。Bachman和Janiak[1]研究了一些单机排序问题,其中工件加工时间是与位置相关的递增或递减函数。Wang等[2]考虑了一些位置相关的加工时间单机排序问题。Liu等[3]研究了带有位置相关加工时间的双代理单机排序问题。Rudek[4]分析了带有位置相关加工时间的两机流水车间调度问题的计算复杂性。Mosheiov等[5]研究了带有位置相关加工时间的单机及时调度问题。Huang和Wang[6]考虑了带有时间和位置相关的加工时间的单机成组调度问题。Liu[7]研究了带有位置相关的加工时间的共同工期窗口指派的成组调度问题。Agnetis和Mosheiov[8]研究了带有位置相关的加工时间和工件可拒绝的成比例流水车间调度问题。王杜娟等[9]研究了恶化效应下加工时间可控的新工件到达干扰管理问题。李永林等[10]研究了考虑学习效应的多目标流水车间调度问题。周意元等[11]研究了具有学习效应的排序对策。余英和程明宝[12]研究了具有学习和退化效应的单机干扰管理问题。Liu等[13]研究了带有学习效应和迟后的双代理排序问题的分支定界算法。刘春来和王建军[14]研究了具有学习和退化效应的单机干扰管理问题。
关于排序博弈问题的研究,唐国春等[15]对排序博弈进行了综述,给出了排序博弈的分类进展和展望。金霁等[16]研究了加工工件都相同的情况下,由最小的最大完工时间作为加工成本的两人合作博弈问题。顾燕红等[17]研究工件加工时间是开工时间线性函数的情况下,以最小的最大流程时间作为加工成本的两人合作博弈问题。Gu等[18]研究了以最小化最大延误作为加工成本的两人合作博弈问题。Liu等[19]以最小化加权误工任务数作为加工成本的两人合作博弈问题。Liu和Wang[20]研究了带有可变加工时间和共同工期的以最小化最大延误作为加工成本的博弈问题。本文的创新之处在于将工件加工时间与工件加工位置相关的情况引入双代理排序博弈问题中。
二、问题描述
假设有一批待加工的工件集S={S1,S2,…,Sn},由两个代理T={1,2}共同合作完成加工。每个代理都拥有一台机器可用于加工工件,两个代理合作加工这n个工件。假设两个代理存在一个给定的初始加工顺序δ0∶M→{1,2},每个工件在加工过程中不能中断并且只能被加工一次,所有工件在“0”时刻可以开始加工。工件Sj的加工时间pj是关于工件加工位置r的函数,本文研究加工时间具有老化效应或学习效应的两个排序模型,分别如式(1)、(2)所示:
pj=P0+ar
(1)
pj=P0-ar
(2)
式中:P0代表工件的正常加工时间,a>0表示模型(1)中的老化效率和模型(2)中的学习效率;j=1,2,…,n;r=1,2,…,n。因为工件的加工时间必须大于零,所以在模型(2)中学习效率a 两个代理的加工成本定义为各自的完工时间,确定这批工件的一个划分,把工件分配给两台机器加工。比较代理在不同加工顺序的加工费用与初始顺序加工费用之间的差值,即代理加工工件费用的节省值,目的是找到这两个代理加工总费用节省的最大值。 用ti来表示工件i的完工时间。工件i的完工时间等于工件i的开始加工时间ti-1与工件i的加工时间pi之和,即ti=pi+ti-1。 假设给定代理加工工件集S的初始加工顺序为δ0,代理加工工件集合S所需的总费用即为代理加工各个工件的加工费用之和,可用C(δ0,S)来表示。则有 (3) 若工件集合的最优加工顺序为δ*,则最优加工顺序下的加工成本为C(δ*,S),从而这两个代理加工该批工件的最大化费用节省可表示为 v(S)=C(δ0,S)-C(δ*,S) (4) 工件i的等待时间可以表示为 (5) 从而工件i的完工时间为 (6) 上式可简化为 (7) 工件集S的最大化费用节省v(S)的具体求解过程如下: C(δ0,S)-C(δ*,S) (8) 两个代理合作加工工件集合S的总费用可表示为 (9) 代理加工这批工件的最大化费用节省为 v(S)=C(δ0,S)-C(δ*,S)= (10) 因为代理加工工件集S的初始加工顺序是给定的,所以可以假设工件划分为由代理1加工的工件集T1和由代理2加工的工件集T2,并且满足T1∩T2=∅,T1∪T2=S,则加工这批工件的最大化费用节省可以表示为 C(δ0,T1)-C(δ*,T1)+C(δ0,T2)-C(δ*,T2)= v(T1)+v(T2) (11) 图1 初始加工排序结果 图2 最优加工排序结果 由此可知,跟初始工件加工顺序相比,最优加工顺序下的工件加工成本费用节省了12个单位,两个代理加工工件的总成本下降了8.7%。 用ti来表示工件i的完工时间。工件i的完工时间等于工件i的开始加工时间ti-1与工件i的加工时间pi之和,即ti=pi+ti-1。假设给定代理加工工件集S的初始加工顺序为δ0,代理在初始加工顺序下加工工件集合S所需的总费用可表示为 (12) 如果用δ*代表工件集S的最优排序,则最优加工顺序下代理的加工成本就为C(δ*,S),从而代理加工这批工件的最大化费用节省可表示为 v(S)=C(δ0,S)-C(δ*,S) (13) 工件i的等待时间可以表示为 (14) 从而工件i的完工时间为 (15) 工件i的完工时间可简化为 (16) 两个代理合作加工工件集合S的总费用可以表示为 (17) 代理加工工件集S的最大化费用节省v(S)的具体求解过程可以表示如下: C(δ0,S)-C(δ*,S) (18) 则这两个代理加工工件集合S的总费用为 (19) 加工这批工件的最大化费用节省为 v(S)=C(δ0,S)-C(δ*,S)= (20) 因为给定代理加工工件集S的初始加工顺序,所以可以假设工件划分为由代理1加工的工件集T1和由代理2加工的工件集T2,并且满足T1∩T2=∅,T1∪T2=S,则代理加工这批工件的最大化费用节省可以表示为 C(δ0,T1)-C(δ*,T1)+C(δ0,T2)-C(δ*,T2)= v(T1)+v(T2) (21) 图3 初始加工排序结果 图4 最优加工排序结果 由此可知,跟初始工件加工顺序相比,最优加工顺序下的工件加工成本费用节省了36个单位,两个代理加工工件的总成本下降了14.63%。 本文将老化效应和学习效应引入双代理排序博弈问题,以完工时间作为加工费用,研究了工件加工时间随着加工序列中工件加工位置的改变而呈现出递增或递减的情况,并以算例具体说明。未来可进一步深入研究的方向包括:考虑其他的目标函数,如最小化最大延迟、加权总完工时间、加权总延误等;考虑三个及以上的代理调度问题。三、具有老化效应的双代理排序博弈
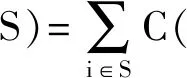
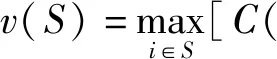
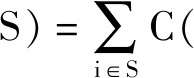


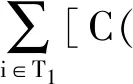
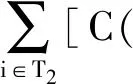
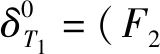


四、具有学习效应的双代理排序博弈
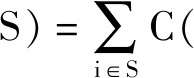
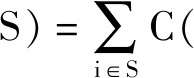
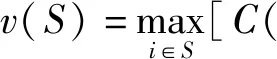
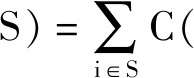


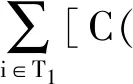
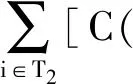


五、结 论
