以“情景”促兴趣 以“变式”促提升

文/佛山市南海区大沥镇河西小学 伍尚燕

“情景与变式”就是在课堂中为要学习的知识创设情景，使学生明白知识的发生过程，并在熟练掌握知识之后能对知识进行变式运用。知识发生过程，可以是引入该知识的原因，也可以是积累从实际情景中提炼数学模型的经验等。“变式运用”，即对知识运用能举一反三，一般通过变更情景、变更条件、变更结论对知识进行拓展运用来实现。下面来谈谈如何通过创设“情景与变式”，来提高学生的学习兴趣，调动学习积极性，提高课堂效果。

一、以“情景”促兴趣

《数学新课程标准》指出：数学教学要紧密联系学生的实际，从学生的生活经验和已有知识出发，在新知引入阶段、新知建构阶段、知识运用阶段，创设各种情景；为学生提供从事数学活动的机会，激发学习数学的兴趣和提高学生的创新能力，打造数学高效课堂。

(一)新知引入阶段设趣味性情景

在新知引入阶段我们可以根据教学内容的需要，引用与学生生活息息相关的故事、动画、谜语、歌曲、游戏、诗歌等生活情景，把学生的注意力、好奇心吸引住，激发学生学习的积极性。

如五年级上册“分数的基本性质”的情境引入如下。

课件演示：一天，唐僧化缘得了三个一样大小的饼，望着那香喷喷的饼，孙悟空和猪八戒馋得口水直流。唐僧把第一个饼平均分成2份，给了大师兄悟空1份； 第二个饼平均分成4份，给了沙和尚2份；猪八戒更贪心啦，对师父说 ：“我要4份，我要4份。”唐僧又把第三个饼平均分成8份，给了猪八戒其中4份。同学们猜猜悟空、八戒、沙僧三人哪个分得多？

学生听后，纷纷发表自己的意见。

师：聪明的唐僧是用什么方法来满足三人的要求，又分得那么公平呢？

把数学知识蕴藏在有趣的故事中，不仅激发了学生的学习兴趣，更让学生在故事中体验数学思想，有效地增进了课堂教学效果，为打造高效课堂奠定基础。

(二)新知建构阶段创设动手实践的情景

在新知建构阶段创设动手实践的情景，让学生在操作中建立数学模型，领悟知识的本质。

如教学“1000以内数的认识”一课，为了让学生掌握数数的方法，我设计了一个动手数一数、填一填的教学情景。

师：老师送给每个小组一份礼物，猜一猜是什么？

师：礼物就在组长的抽屉里，请小组长拿出来。

生：是小棒。

师：对，是小棒。礼物里既有单根小棒，也有1小捆，还有大捆的？那你们知道1小捆里有多少根吗？请同学们小组合作，把这些小棒数一数，算一算，怎样能又准又快地数出来，并填写小实验。

小实验

通过数数我发现：

一个一个地数，10个一是( )，

一十一十地数，10个十是( )，

一百一百地数，10个一百是( )。

用生活中司空见惯的“数小棒”入手，创设动手操作的情景，将学生引入这堂课的重点：相邻计数单位之间十进制的关系。这样一来，巧妙地把一些枯燥而抽象的数学规律变得生动有趣，使他们在愉快，和谐的课堂氛围中突破了知识的难点。

(三)知识运用阶段创问题情景

知识运用阶段创问题情景可以给学生带来“数学有用，数学可以解决生活问题”的体验感和愉悦感。因此老师要基于学生的学习规律设计多层次的认知挑战，可以是有关记忆的、理解性的、探究性的。让学生对应模型，再回归到现实生活问题解决的开放过程。

如《1000以内数的认识》练习，我设计了一个跳飞机游戏。

师：课前我们已经玩了1到100以内数跳飞机的游戏，现在我们再来玩从500开始跳到1000的游戏，看哪个小组的同学跳得又快又准确。

跳飞机游戏规则：1.先掷骰子，确定点数。2.根据点数，读出棋子经过的数字。3.如果遇到飞机则按路线飞行。

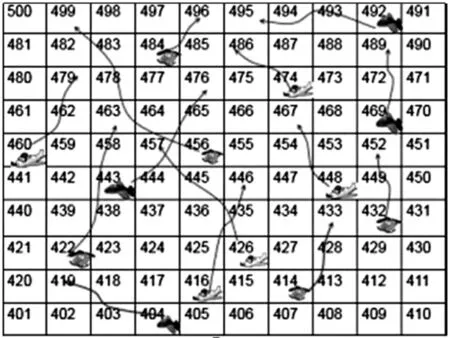
课的结尾学生注意力相对比较散漫，这时老师就要设计能吸引学生注意力的情景，这样既让学生从情景中捕捉到数学信息，又用数学知识去解决了身边的问题，提高了学生数学学习能力和应用能力。

在课堂教学的新知引入、建构、运用等环节创设情景，做到以情育人、以景导学；既让学生体验了“知识源自生活，知识源自情景”，又激发了学习兴趣、提高教学效果。

二、以“变式”促提升

通常，在课堂中每学了一道例题或解答了一道题的答案，我们都可以理解为“完成了”，就是说对于该题的任务就结束了，其实不是的。假如做完一道题后，老师引导学生在此基础上再多走一步，收获将是倍增的，这一步就是变式训练。变式训练可以是对问题的变式、对条件的变式，也可以是对问题、条件同时作较深层面修改的变式；一般条件变式有以下类型。

(一)条件数据的修改

例如：

这是一年级一道连加的计算题，显然是考查学生对“三个数合并成一个数的运算”方法的运用。变式：把题中第二、三个数据“3 ”“1”，分别修改为“2”和“2”。改动之后，计算对比，一方面巩固了4的组成，“4可以分成3和1 ”“4可以分成2和2”。另一方面，也让学生直观地感知了“一个加数增加1，另一个加数减少1，结果不变”的现实。数字的变化，既训练了学生做题、审题时认真的态度，同时也提高了学生的观察能力。

(二)条件次序的修改

再来把上面题目进行变式：把数据一与数据二对调位置，看似简单甚至无必要，其实不然。解题时，学生经过计算对比发现，加数位置对换后，计算结果不变这一现象，为以后学习加法交换律提供了浅层表象，积累下了感性的现实认知。

(三)条件的补充

例如：

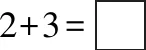
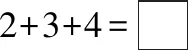
题目要训练的是让学生把分步算式整合成综合算式的能力。变式：把条件2中的“5”隐去，用方框代替。这样的改变是让学生注意到，第二步的计算要用到第一步计算的结果。这样改变更重要的是，它的“一弱化一强化”的作用，就是说第一步的计算结果在综合算式里不显示的，强化的是2、3、4三个数据在综合算式的出现。

填一填 圈一圈，填一填

本题的变式带有开放性，圈去的不同，剩下的就不同，条件变了，所求问题的结果就变了。当然，这个条件得由学生自己补充。最后可以追问一句“我一个都不圈，第二步应减去什么”。这样的变式培养了学生的思维能力和创新能力。

(四)条件的延伸

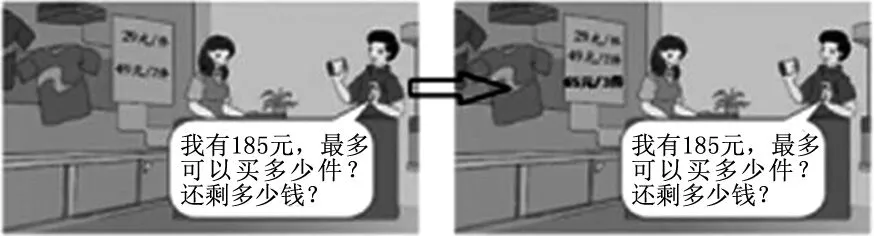
这是四年级下册的题目，是一道开放题，学生会有难度。题中有两个标价，一个总价，问最多可以买到多少件？还剩多少钱？解决这个问题，学生要用到总价、单价和数量三者间的数量关系式。更为重要的是，它的解题过程还要策略方面的思考，进行策略的选优。

两种标价就有两种单独的买法，考虑到“最多”还有一综合的买法。对比发现“多买合算”这一普遍的交易现象。提炼方法：先两件两件的买，再用剩余的钱一件一件的买，能买到最多。

变式：从原条件中延伸出第三个条件“65元/3件”。

有了前面的基础，同学们会首先把三个标价作对比，找出合算的买法，三件三件的买——两件两件的买——一件一件的买。这样的变式训练，锤炼了技能，提升了方法。

可以把变式的主动权交给学生，让学生自己思考如何把题目进行变式，如何解答。数学变式训练无时不在，在教学过程中，教师要加强知识的整合，系统的优化，能力的拓展，让学生真正实现一题一得，一题多得，融会而贯通。

以上是对“情景与变式”提高课堂效率的一点见解，在教学工作中我们要做一个“情景与变式”的有心人，通过以“情景”吸引学生学习兴趣、以“变式”提升课堂教学效果。