含负折射率材料的一维双周期光子晶体带隙特性

2020-05-05蔡培君廖同庆

沈阳大学学报(自然科学版) 2020年2期

蔡培君, 廖同庆

(1. 安徽大学江淮学院理工部, 安徽合肥 230039; 2. 安徽大学电子信息工程学院, 安徽合肥 230601)

光子晶体是由折射率不同的介质周期性排列构成的规则光学结构.这种周期性结构能够阻断特定频率的光子在光子晶体内部的运动,使光子晶体表现出带隙特性[1-2].根据构成光子晶体的材料的空间分布特点,可以将光子晶体分为一维光子晶体、二维光子晶体和三维光子晶体.一维光子晶体由几种折射率不同的材料在空间中沿某一个方向进行周期排列构成,其在其他方向上的折射率不变.由于其制备简单,受到了学者们的广泛关注,成为近几年的研究热点.

目前根据一维光子晶体的禁带特性及其缺陷模式的带隙特性制成的光学器件已被广泛应用于很多领域,如窄带滤波器、光开关、传感器、激光、反射器等[3-7],构成这些光学器件的一维光子晶体基本是由常规折射率材料(材料的折射率n,介电常数ε和磁导率μ均大于零)组成的.负折射率材料,又称为左手材料,介电常数ε和磁导率μ至少有一个为负值,因此光波在左手材料中的传播特性与在右手材料中传播特性不同[8-13].所以,在常规的一维光子晶体中引入负折射率材料能够改变其光学性能,其带隙特性必随之而改变[14-15].

本文首先研究了含负折射率材料的一维双周期光子晶体的带隙特性,进而分析在一个禁带周期中其禁带宽度加宽的物理机理,最后分析了构成含负折射率材料的一维双周期光子晶体的子周期数、薄膜厚度和相对折射率差对其带隙特性的影响.

1 结构及传输矩阵

设含负折射率材料的一维双周期光子晶体((AB)m1(BA)m2)N由2种折射率不同的材料构成,其结构如图1所示.其中媒质A为右手材料,折射率为n1,媒质B为左手材料,折射率为n2,且2种媒质的物理厚度分别为d1和d2,则构成的一维光子晶体的单个周期单元的厚度d=d1+d2;设m1和m2为一维双周期光子晶体的子周期数,且m1=m2=m,则子周期厚度满足dm1=dm2=md;N为一维双周期光子晶体的周期数,设其总厚度为dN,且满足

dN=N(dm1+dm2)=2Nmd.

当光波垂直入射(入射角θ=0°)到光子晶体左侧时,单层媒质的传输矩阵为

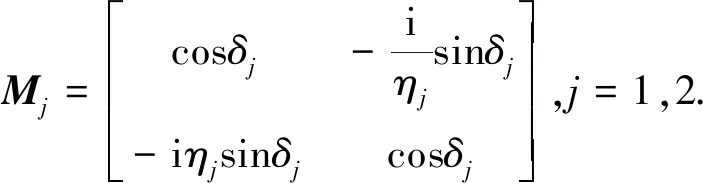
(1)

式中,δj为光波穿过单层媒质时变化的相位,媒质为右手材料时δj=2πnjdjcosθj/λ;媒质为左手材料时δj=-2πnjdjcosθj/λ.ηj=(ε/μ)1/2cosθj,θj为光波入射到第j层媒质的折射角,dj为第j层媒质的物理厚度,λ为入射光波长,i为虚数单位.

图1 含负折射率材料的一维双周期光子晶体结构Fig.1 The structure of one-dimensional double periodic photonic crystals containing negative refractive index materials

光波经过单个子周期单元AB和单个子周期单元BA的传输矩阵如式(2)、(3)所示:

进而可以得到光波经过结构为((AB)m1(BA)m2)N的一维双周期光子晶体的传输矩阵为

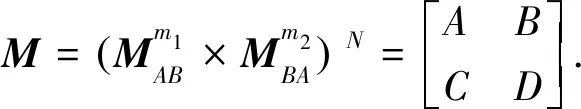
(4)

根据式(4)可以计算出结构为((AB)m1(BA)m2)N的一维双周期光子晶体的透射率和反射率分别为

根据式(5)、式(6),利用传输矩阵法可以绘制出含负折射率材料的结构为((AB)m1(BA)m2)N的一维双周期光子晶体的透射率曲线和反射率曲线,进而研究其带隙特性.

2 带隙特性

2.1 禁带

分别选取2种构成结构为((AB)m1(BA)m2)N的含负折射率材料的一维双周期光子晶体和常规一维双周期光子晶体,其折射率如表1所示.

表1 一维双周期光子晶体材料折射率Table 1 Refractive index of one-dimensional biperiodic photonic crystal materials

设常规一维双周期光子晶体的中心波长λ0=1 064 nm,子周期数m=2,周期数N=10,各层薄膜材料的光学厚度均满足1/4中心波长,即n1d1=n2d2=λ0/4.为与常规一维双周期光子晶体类比,设定含负折射率材料的一维双周期光子晶体的中心波长λ0=1 064 nm,子周期数m=2,周期数N=10,各层薄膜材料的光学厚度满足n1d1=-n2d2=λ0/4.

当光波垂直入射到光子晶体表面时,可以得到光子晶体的透射率随入射光归一化频率的变化曲线,如图2所示.

由图2可知,含负折射率媒质的一维双周期光子晶体仅在ω=ω0/2和ω=3ω0/2处出现禁带,禁带数目少于常规媒质构成的一维双周期光子晶体,但禁带宽度明显加宽,并且在ω=ω0处出现尖锐的导带,导带的半波高宽约为44 nm.

2.2 禁带加宽的机理分析

由于含负折射率材料的一维双周期光子晶体的单个子周期中,两层薄膜厚度满足n1d1=-n2d2=λ0/4,因此光波通过单个周期单元时,反射波相对于入射波的相位差为零,此时反射波与入射波相长干涉.即入射波被全部反射,形成禁带.

根据布拉格散射定律可知,

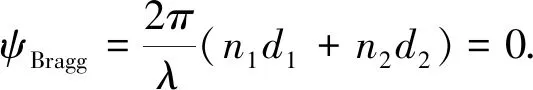
(7)

由公式(7)可知,入射光波一定时,光波在单个周期单元内传播时,反射波与入射波总的相位变化为0.因此光波在整个光子晶体内传播时,在入射表面,反射波相对于入射波的相位变化为0,即出现相长干涉.

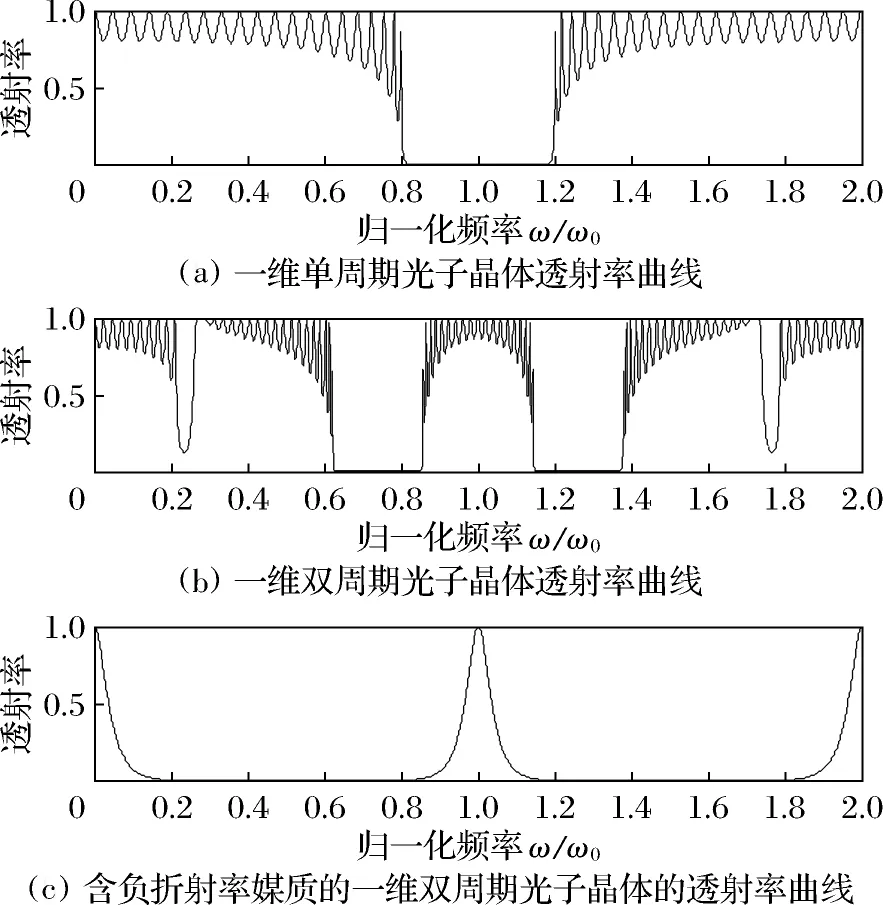
图2 一维光子晶体透射率曲线对比

Fig.2 Comparison of transmittance curves of one-dimensional photonic crystals

因此在禁带中心ω=ω0/2和ω=3ω0/2处,反射波在入射面上出现相长干涉,出现高反带,因此禁带特性表现为平整的禁带;当入射光频率偏离ω0/2和3ω0/2时,此时法布里-珀罗谐振虽然已经开始作用,但是由于相长干涉的作用,透射率并没有快速上升,此时仍表现为平坦的禁带;随着入射光频率的进一步增加,法布里-珀罗谐振开始起主导作用,当光波垂直入射时,根据法布里-珀罗谐振相位差公式可知,

ψF-P=(2π/λ)nidi.

(8)

根据式(8)可得,法布里-珀罗谐振相位差随着入射光波长变化而变化,当入射光频率达到ω=ω0时,此时在单个子周期单元内,法布里-珀罗谐振相位差达到π的整数倍,透射率达到最大值,此处即为导带中心.

3 带隙特性的影响因素

3.1 子周期数对带隙特性的影响

取含负折射率材料的一维双周期光子晶体的子周期数m从1～9变化时,分别绘出相应的透射率曲线,如图3所示.

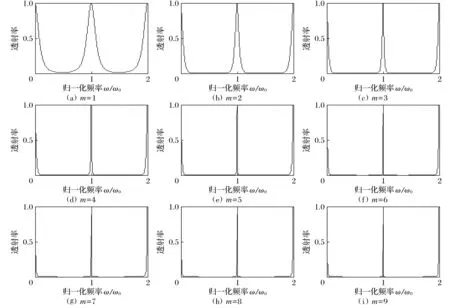
图3 不同子周期数含负折射率材料的一维双周期光子晶体透射率Fig.3 The transmittance of one-dimensional biperiodic photonic crystals containing negative refractive index materials with different subperiod numbers

由图3可知,随着含负折射率材料的一维双周期光子晶体的子周期数的增加,禁带中心位置不变,但禁带宽度逐步增加,在ω=ω0处的透射峰随子周期数的增加变得更加尖锐,且当m从1～9变化时,透射峰的半波全宽分别为180.02、76.70、34.06、14.90、6.38、2.13、0、0、0 nm,由此可见,随着子周期数的增加,透射峰的半波全宽逐步减小,当子周期数达到7左右时,此时透射峰的半波全宽为零,而当子周期数进一步增加时,透射峰的半波全宽稳定在零值,不再随着子周期数的增加而变化.

3.2 薄膜厚度对禁带特性的影响

设组成一维双周期光子晶体的两种薄膜厚度满足n1d1=n2d2=αλ0,其中α为薄膜厚度系数,组成含负折射率材料的一维双周期光子晶体的材料的折射率如表1所示,当子周期数m=2,周期数N=10保持不变,当薄膜厚度系数α分别取1/8、1/4、1/2和1时,光子晶体的透射率曲线如图4所示.

观察图4可以发现,随着薄膜光学厚度的成倍增加,在归一化频率0～2.0之间导带仍然为尖锐的透射峰,禁带平坦, 但带隙宽度不断减小,带隙个数成倍增加.此特性,为梳状滤波器的设计提供了坚实的技术支撑.

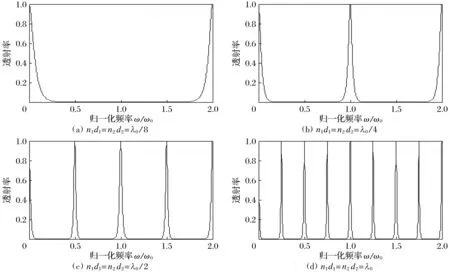
图4 不同薄膜厚度下的含负折射率材料的一维双周期光子晶体透射率Fig.4 The transmittance of one-dimensional biperiodic photonic crystals in materials with negative refractive index with different film thicknesses

3.3 正负折射率材料的相对折射率差对禁带的影响

取3组负折射率不同的材料,材料的相对折射率见表2.设定2种媒质的薄膜厚度满足n1d1=n2d2=λ0/4,入射光波长λ0=1 064 nm,当光波垂直入射到光子晶体表面时,3组不同折射率材料组成的一维双周期光子晶体透射率曲线如图5所示.

表2 3组不同材料的折射率Table 2 The refractive index of three different groups of materials

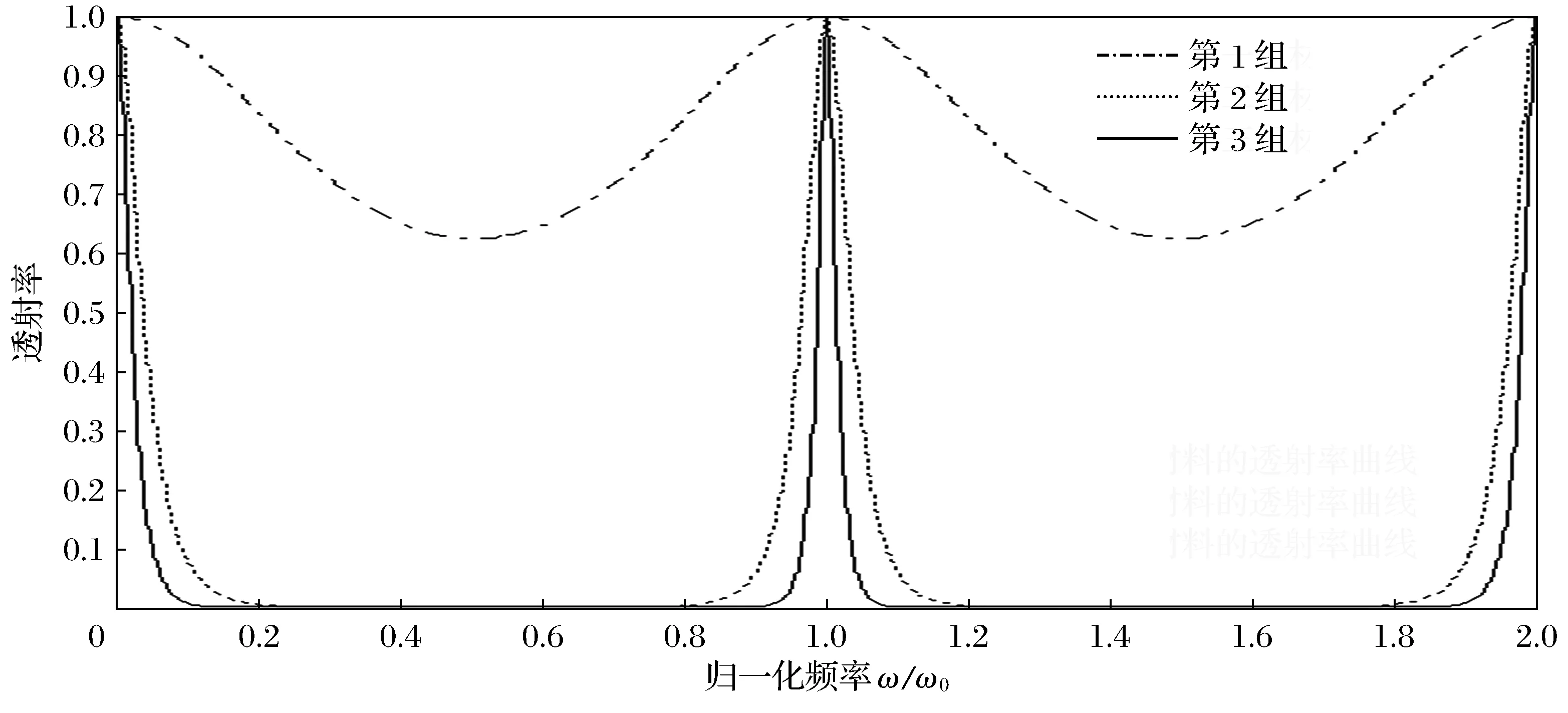
图5 不同折射率差的一维双周期光子晶体透射率Fig.5 The transmission of one-dimensional biperiodic photonic crystals with different refractive index differences

观察图5可以发现,含负折射率材料的一维双周期光子晶体和常规材料构成的一维光子晶体一样, 构成光子晶体的媒质的相对折射率差影响了光子禁带特性.即,当构成光子晶体的右手材料一定时,随着人工合成的负折射率材料的折射率模值的增加,构成光子晶体的2种材料的相对折射率差越大,此时光子带隙特性越明显,且禁带宽度越大,禁带越平坦.