质量特性对航天器火工冲击传递影响仿真分析
2020-05-04
中国空间技术研究院 通信卫星事业部,北京 100094
航天器火工冲击环境是指航天器上火工品起爆时刻产生的高频瞬态冲击载荷作用在结构上的响应[1],如卫星与运载火箭的末级分离,卫星舱段分离,星载伸展部件展开过程中的解锁、释放和分离等[2],具有瞬态、高频和高量级的特点[3]。卫星承受冲击载荷时,冲击能量迅速传递,可能造成卫星结构以及仪器设备的损害和故障。
为对火工冲击传递特性进行预示分析,国内外经过大量研究给出了多种方法。文献[4]中根据大量试验数据给出了在不同结构上冲击的衰减规律以及点源下冲击传递的经验公式;文献[5]给出了冲击环境下不同结构连接以及距离对冲击响应的影响函数。两者均依靠工程实际及试验数据对冲击传递特性进行了经验性总结,但并不能对每颗卫星进行针对性分析。文献[6]使用有限元法对复合材料板上火工冲击远场响应进行了仿真分析,但并未考虑质量因素的影响;文献[7]建立了机箱结构与电子设备的连接模型,给出了火工冲击环境下机箱内部电子产品的冲击响应分析方法。上述研究从距离、连接结构等不同方面描述了火工冲击的传递特性。但在真实情况下,卫星结构复杂,舱板上分布大量单机设备,其质量特性会对冲击传递产生影响,上述研究缺少对此方面的分析,需要对单机设备进行建模及分析。
本文使用显式有限元法,应用MSC.Dytran软件,以太阳翼解锁过程为研究对象,对卫星舱板及单机设备进行有限元建模,使用组合脉冲函数模拟冲击源载荷,对火工冲击在垂直舱板方向的响应进行仿真计算。通过与试验实测数据对比,验证方法的可行性,并得到质量特性对火工冲击传递影响的规律。
1 冲击响应传递及衰减机理分析
当冲击载荷动态加载到结构时,其响应传递需要一定时间,结构各部位之间是不平衡的。在分析舱板火工冲击响应时,除考虑单机设备与舱板之间的螺栓连接外,由于单机底板面积较大并与舱板发生接触,因此也会发生一定的相互作用。在舱板与单机设备构成的局部系统中,冲击的传递体现在应力波的传播以及结构的惯性效应两个方面[8]。
1.1 应力波的传播
当舱板厚度方向受到冲击载荷时,会在厚度方向引起应力波的传播,由于其厚度方向尺寸远小于其他方向的尺寸,应力波会在厚度方向来回反射。当应力波传播至舱板与单机设备底板的边界时,由于二者的波阻抗(介质密度×波速)不同,会在接触界面发生波的反射与透射。由于仅研究舱板在厚度方向的冲击响应,因此可将舱板内的应力波简化为一维横波,此时在交界面处将只反射和透射横波,如图1所示。
透射波、反射波与入射波的应力幅值关系为[9]:
(1)
(2)
式中:σI、σT、σR分别为入射波、透射波和反射波的应力幅值;ρAcA和ρBcB分别为卫星舱板和单机设备的机械阻抗。当两种介质的机械阻抗相等时,应力波完全透射,否则会产生反射波,其方向取决于两种介质机械阻抗的大小关系。因此,舱板与单机设备之间会以应力波的透射与折射进行能量传递,并在实际的接触情况下存在一定的传递效率。
1.2 结构的惯性效应
当应力波不足以使材料失效时,在极短的时间内,应力波经过多次反射,使厚度方向应力趋于零应力状态,但在舱板不同位置处产生了一定的速度,使舱板产生了动态变形,此时转变为持续时间较长的结构动态响应,即结构的惯性效应。由于应力波作用时间远小于结构动态响应过程,因此在分析结构动态响应时,可忽略应力波的影响。
冲击响应在卫星舱板与单机设备之间的传递可以简化为二自由度阻尼系统的自由振动,如图2所示。
在冲击源处施加冲击载荷后,结构响应开始在舱板上传递,当响应传递至单机设备处时,舱板与单机设备的振动相互耦合,可看作具有一定初始条件的二自由度阻尼系统自由振动。舱板的刚度与阻尼可等效为k1和c1;舱板与单机设备之间由于接触挤压产生的弹性变形,视为刚度作用,用k2表示;由表面不平整而产生的塑性变形,视为阻尼作用,用c2表示。由此可见,舱板自身对结构响应具有衰减作用,并在与单机设备的接触间进行能量的传递、耗散。
经过上述分析,在冲击的两种传递方式下,单机设备均使舱板上的冲击响应衰减。因此,在研究冲击响应的传递规律时,质量特性成为不可忽略的因素。根据冲击响应的传递机理,卫星舱板与单机设备间的响应传递多发生在两者的接触面上,因此对卫星舱板及单机设备进行冲击有限元建模时,在考虑质量大小、质心位置、截面转动惯量等要素的同时,还应对底面接触进行建模分析。
2 火工冲击响应仿真分析
2.1 卫星舱板布局特性
本文以太阳翼解锁过程为研究对象,进行火工冲击响应分析。太阳翼火工品压紧点位于卫星通信舱南北板,两个舱板上分别有8个火工品分5次进行起爆。在部分火工品压紧点附近的150 mm、300 mm、500 mm处布置有冲击加速度传感器,来测量火工品起爆时该测点处的加速度响应。冲击源附近分布有单机设备,通过板内的埋件,使用螺栓与舱板连接。不同火工品压紧点附近单机设备的布局情况不同,选取4个具有不同布局特征的压紧点,其附近的单机布局如图3所示。图3中黑色正方形为太阳翼火工品压紧点,以其为圆心的3个圆分别代表距离冲击源150 mm、300 mm、500 mm的范围;黑色三角形代表冲击加速度传感器粘贴点,即冲击加速度测量点,螺栓为单机设备与舱板连接点。
选取的4个压紧点附近,从布局a~d单机设备分布逐渐增加:其中布局a~c中,测量点路径上无单机设备分布,但路径周围设备分布逐渐增多;布局d中测量点路径上存在单机设备。针对4种布局情况,进行有限元建模与分析计算,并与试验测试数据进行对比,验证有限元建模的合理性。
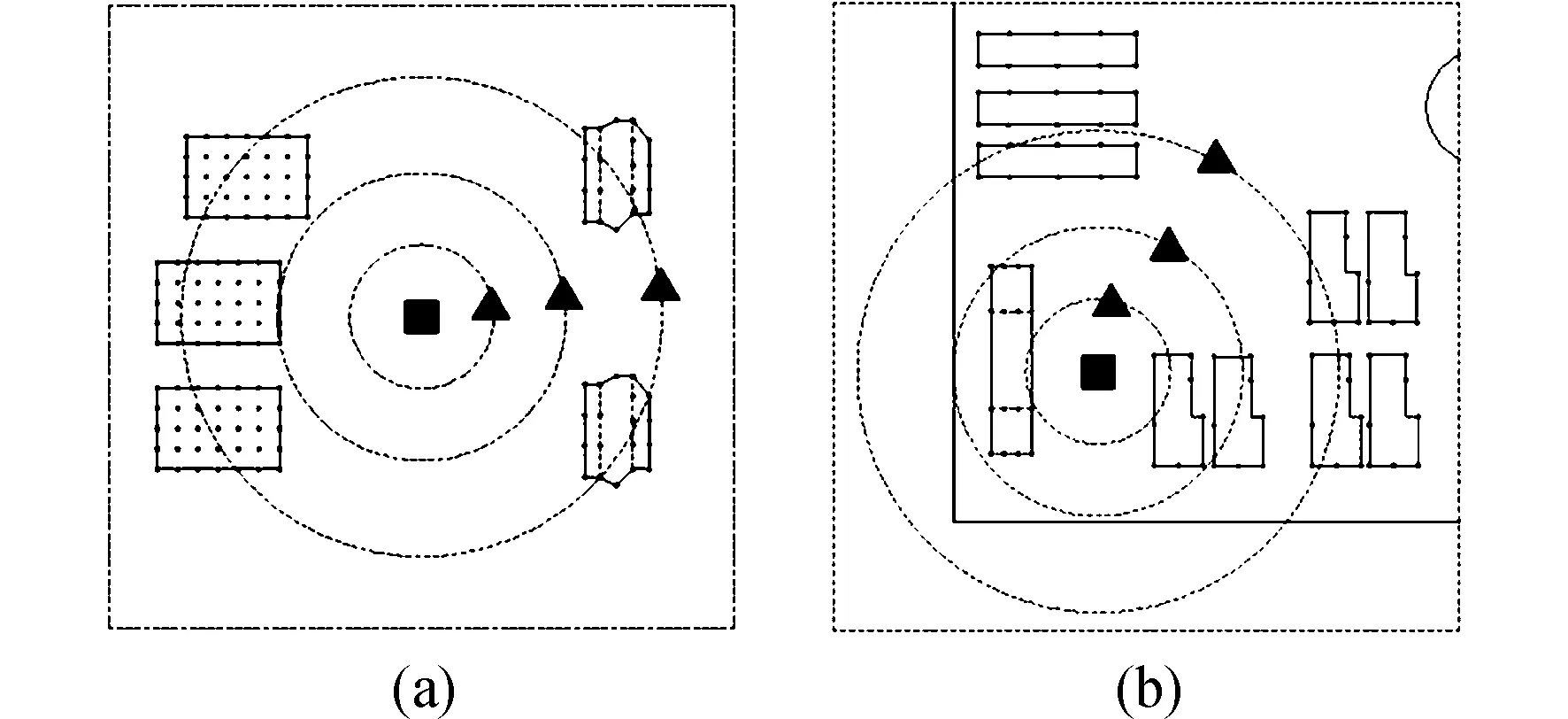

图3 卫星舱板上4个火工品压紧点附近的单机设备布局Fig.3 Layouts of satellite equipment around 4 compression points of initiating explosive devices
2.2 结构有限元建模
使用MSC.Patran建立有限元模型。卫星舱板使用蜂窝夹层板结构[10],将其简化为复合材料板,即shell壳单元,其中上下面板为铝合金材料,采用各向同性材料,厚度0.3 mm,密度2 700 kg/m3,弹性模量70 GPa,剪切模量27 GPa,泊松比0.3;蜂窝芯子采用正交各向异性材料,厚度25 mm,密度104.8 kg/m3,其材料参数只定义垂直板面方向的剪切刚度为112 MPa。这种建模方式可以真实地模拟舱板受力情况,使弯曲刚度由面板提供,剪切刚度由芯子提供。网格使用面四边形单元(Quad4),网格尺寸为10 mm,四周采取固支边界条件。
单机设备根据其外形及质心位置简化为线弹性材料的立方体,模拟单机的质量特性及转动惯量。单元模型采用拉格朗日体单元,网格使用六面体单元(Hex8),网格尺寸为10 mm。单机设备在螺栓连接处使用刚性多点约束(MPC)与舱板连接,限制平动与转动自由度。在单机设备底面与舱板之间建立主-从面接触,模拟两平面之间的相互作用,并防止穿透现象的发生。对于板壳单元的结构碰撞问题,由于单元节点取在板壳结构的中性层上,为真实模拟发生接触的位置,须考虑板单元厚度及间隙,接触厚度为舱板厚度的一半和单机设备与舱板之间的间隙之和,设置为13 mm。有限元模型如图4所示。

图4 舱板局部有限元模型Fig.4 FEM model of local satellite board
2.3 冲击源载荷
冲击源的冲击特性复杂,冲击量级高,使得冲击载荷函数获取较难。文献[11]中使用梯形脉冲模拟航天器夹具展开时的冲击源力函数;文献[12]中使用三角形脉冲模拟天线展开时的冲击源力函数。因此可采用简单脉冲函数来模拟冲击源力函数,使其能够模拟真实的冲击响应。
本文在火工品起爆点处施加垂直舱板的力函数,模拟火工品起爆时垂直舱板方向的冲击载荷。通过对不同简单脉冲函数进行组合叠加,得到如下结论:脉冲波形影响冲击响应谱走势;幅值影响冲击响应谱的最大值,且呈线性关系;脉宽影响中频段极值点对应的频率。
经过对比大量试验数据,得到冲击源附近冲击响应谱特征,并以上述规律为依据反推冲击源模拟力函数。根据试验数据中冲击响应谱的量级以及频率分布范围,经拟合,使用幅值4 000 N、脉宽0.6 ms的半正弦波脉冲与幅值1 000 N、脉宽0.6 ms的三角形脉冲来模拟冲击源力函数,得到的冲击响应谱与试验实测数据相当,可用来作为冲击源的输入函数。冲击源附近100 mm处的冲击响应谱与多个火工品起爆点附近100 mm处的冲击响应谱对比情况如图5所示。
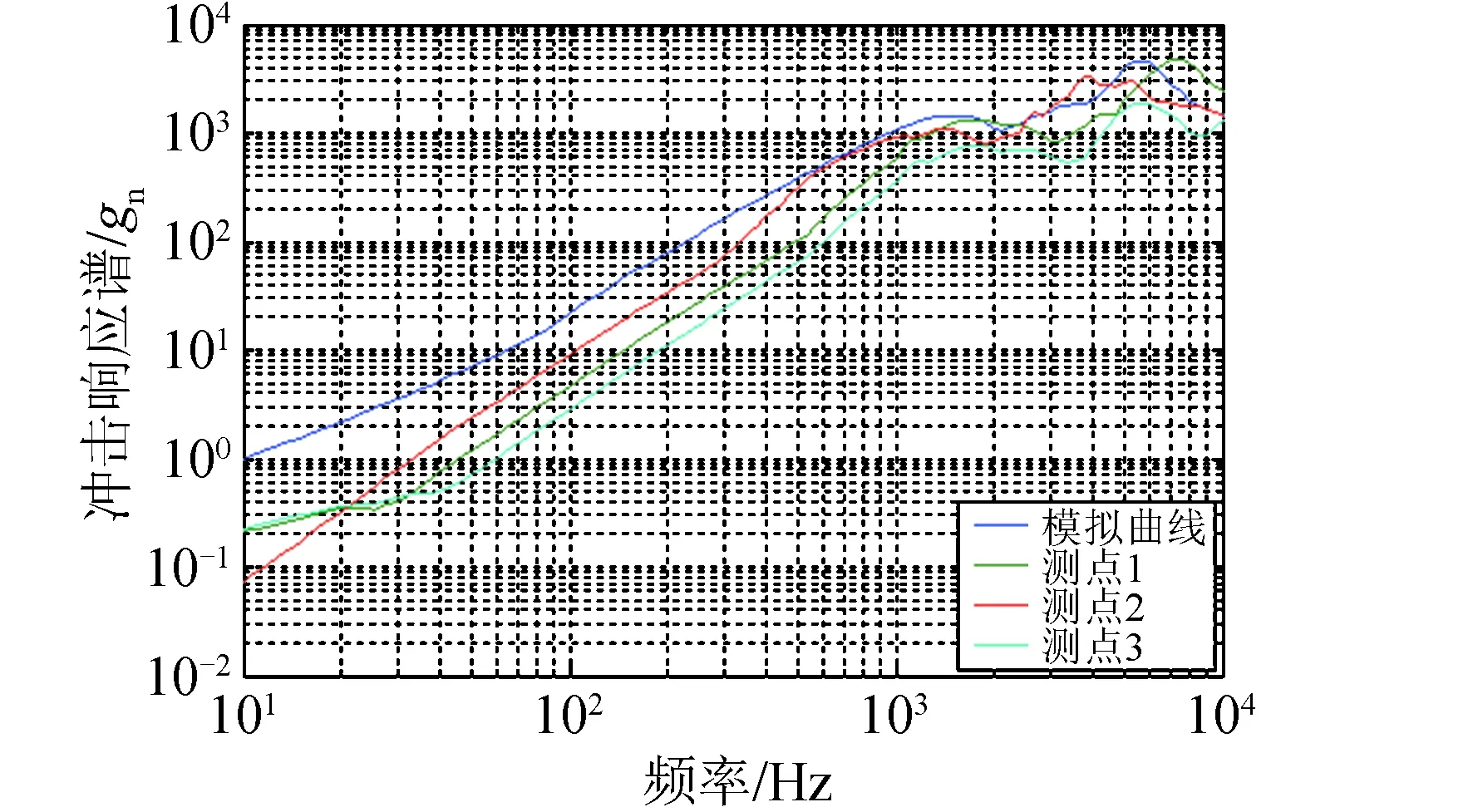
图5 冲击源模拟曲线与试验数据对比Fig.5 Comparison of simulated curve and test data of pyroshock source
2.4 冲击响应分析计算结果
分别对上述4种布局特性进行建模与分析,计算测量点处的冲击响应谱,并与试验数据进行对比。其中试验数据为整星地面太阳翼解锁时的实测数据,其整星布局、测点分布和有限元模型相同。
分别提取仿真计算与实测试验数据的冲击响应谱最大值,并计算二者之间的误差,误差计算公式如下:
(3)
式中:A1和A2分别为分析计算与试验实测数据冲击响应谱的最大值。误差代表了冲击响应谱的相对大小。
(1)布局a
布局a的仿真计算结果如图6所示,分析计算与试验实测数据冲击响应谱最大值与误差如表1所示。


图6 布局a中测量点的冲击响应谱Fig.6 SRS of measuring points in layout a
表1布局a中测量点冲击响应谱最大值与误差
Table 1 The maximum and error of SRS in layout a

距冲击源距离/mm分析计算值/gn试验实测值/gn误差/dB15026752503+0.5830025042280+0.8150019302073-0.62
(2)布局b
布局b的仿真计算结果如图7所示,分析计算与试验实测数据冲击响应谱最大值与误差如表2所示。
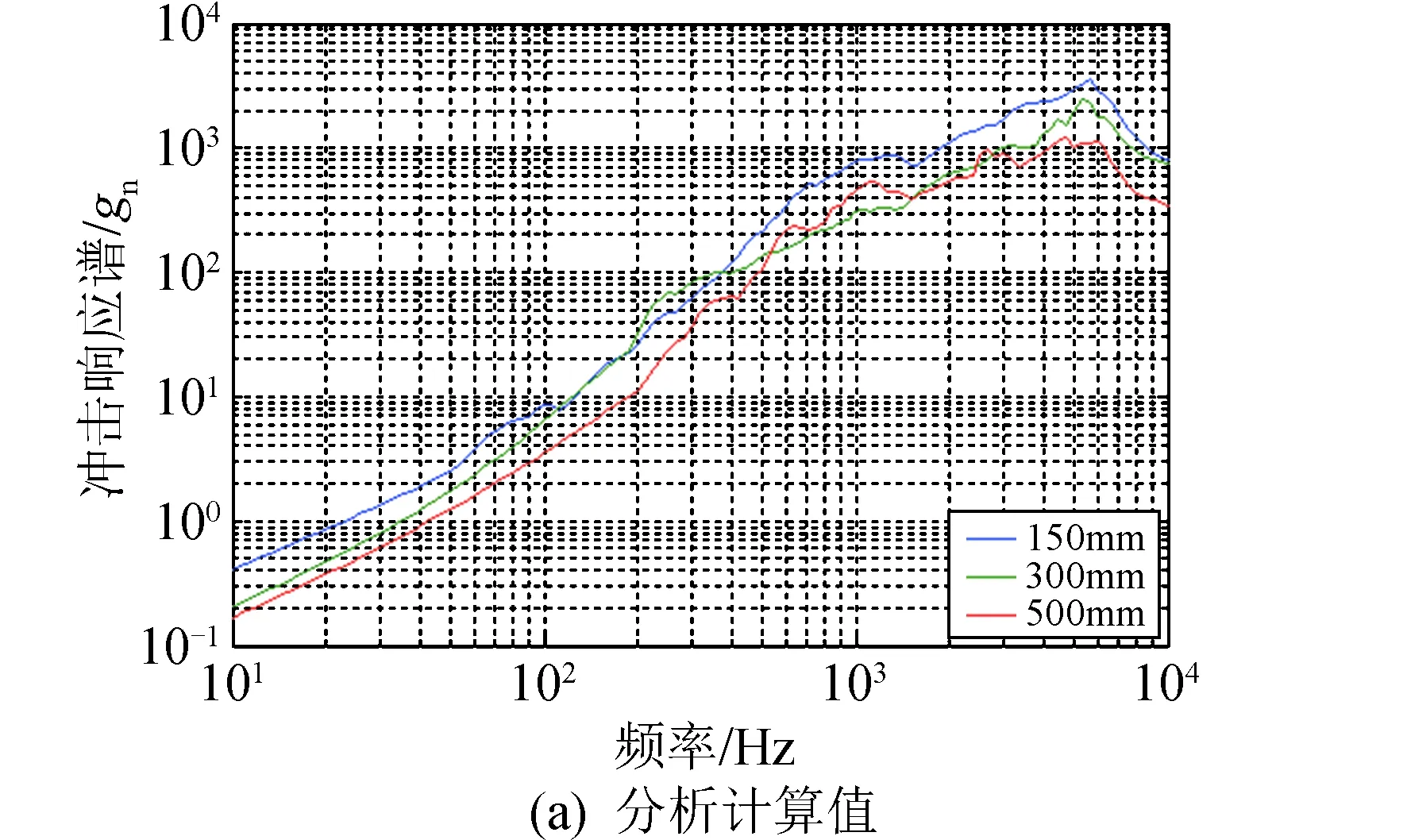

图7 布局b中测量点的冲击响应谱Fig.7 SRS of measuring points in layout b
表2布局b中测量点冲击响应谱最大值与误差
Table 2 The maximum and error of SRS in layout b

距冲击源距离/mm分析计算值/gn试验实测值/gn误差/dB15035282524+2.9130024441683+3.245001206985+1.76
(3)布局c
布局c的仿真计算结果如图8所示,分析计算与试验实测数据冲击响应谱最大值与误差如表3所示。
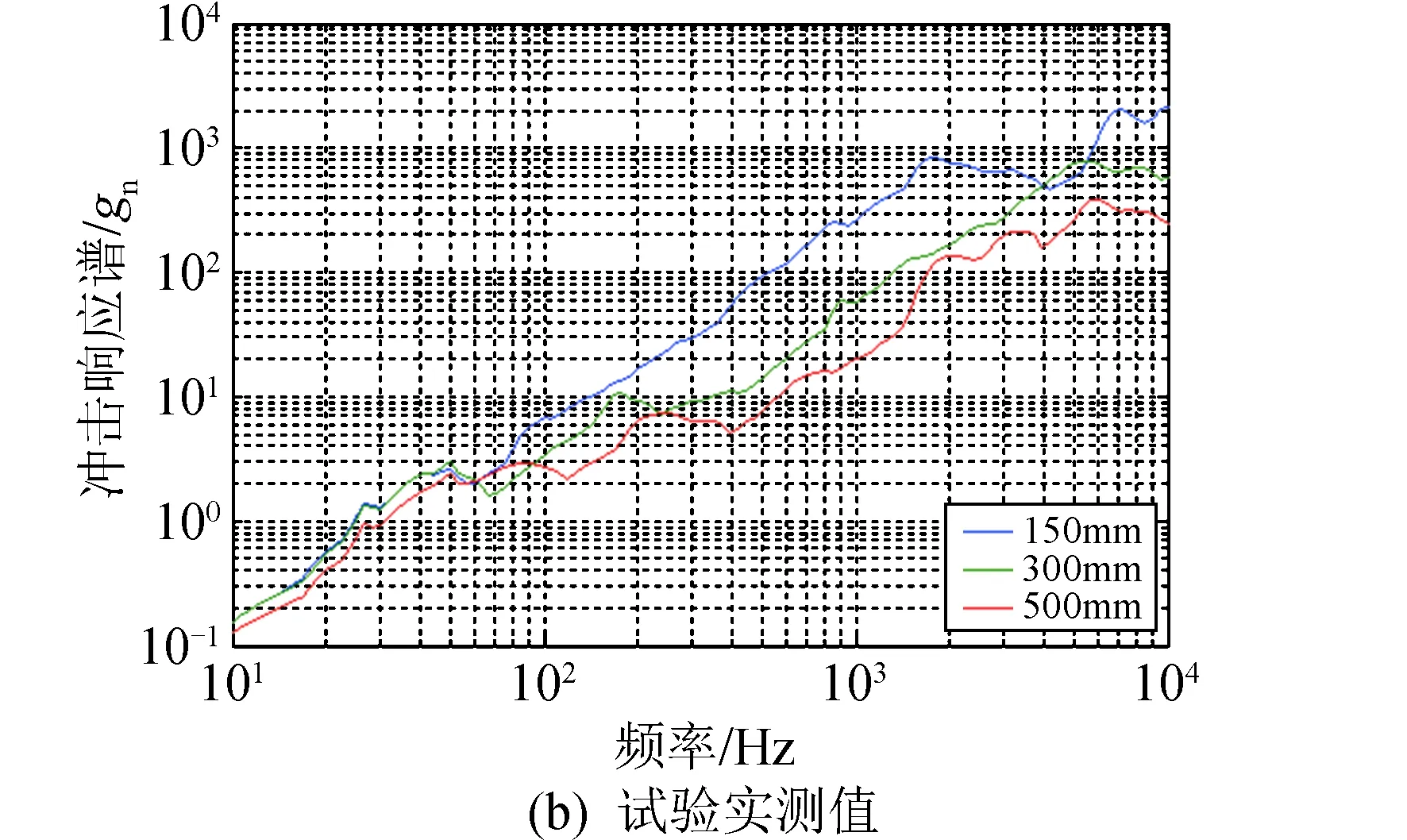
图8 布局c中测量点的冲击响应谱Fig.8 SRS of measuring points in layout c
表3布局c中测量点冲击响应谱最大值与误差
Table 3 The maximum and error of SRS in layout c

距冲击源距离/mm分析计算值/gn试验实测值/gn误差/dB15021102138-0.11300634789-1.90500308390-2.05
(4)布局d
布局d的仿真计算结果如图9所示,分析计算与试验实测数据冲击响应谱最大值与误差如表4所示。
根据分析计算与实测数据的对比,冲击响应谱最大值误差最大为+3.24 dB,最小为0 dB,且冲击响应谱走势相近。在冲击试验中,试验条件容许偏差要求冲击响应谱值与试验条件相差不超过±6 dB,因此在实际工程应用中,此建模方法可以在一定程度上对火工冲击响应进行模拟。
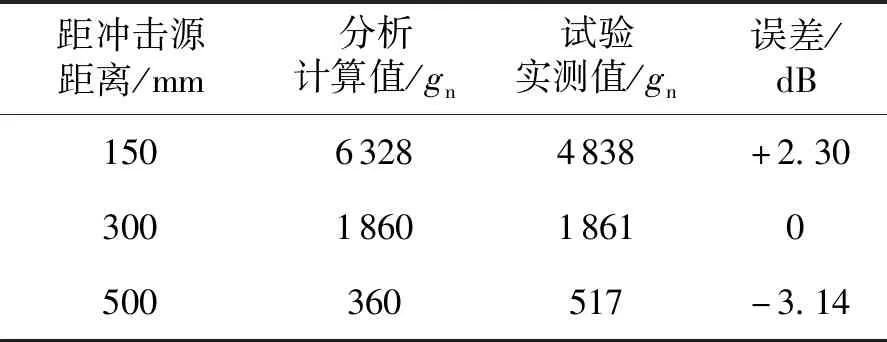
表4 布局d中测量点冲击响应谱最大值与误差Table 4 The maximum and error of SRS in layout d


图9 布局d中测量点的冲击响应谱Fig.9 SRS of measuring points in layout d
2.5 火工冲击衰减特性分析
根据上述仿真计算结果与试验实测数据,垂直板面方向冲击量级随着距冲击源距离的增加而逐渐衰减。在4种仿真计算的布局下,冲击响应的衰减程度不同。
根据表中的数据,分别对分析计算与试验实测数据的衰减情况进行对比,将150 mm处的冲击响应作为基准,对冲击响应量级进行比较,结果如表5、表6所示。
由表5、表6可得,在不同的布局情况下,火工冲击响应的衰减规律有较大差异。从分析计算与实测数据的拟合情况来看,分析结果与实测数据相差不超过10%,能够在一定程度上模拟冲击传递衰减的规律。
从冲击衰减的特性来看,从布局a~d,测点附近的单机设备依次增加。当在测量点附近没有或有极少量单机设备时,冲击衰减现象很小,在500 mm处的冲击响应仍有150 mm处的80%左右。当测量点附近以及传递路线上的单机设备逐渐增加后,冲击响应的衰减现象逐渐明显,500 mm处的冲击响应衰减至30%~40%。当测点之间存在单机设备时,500 mm处的冲击响应衰减至20%以下。

表5 冲击响应衰减情况对比(分析计算)Table 5 Comparison of attenuation of pyroshock response (calculation)
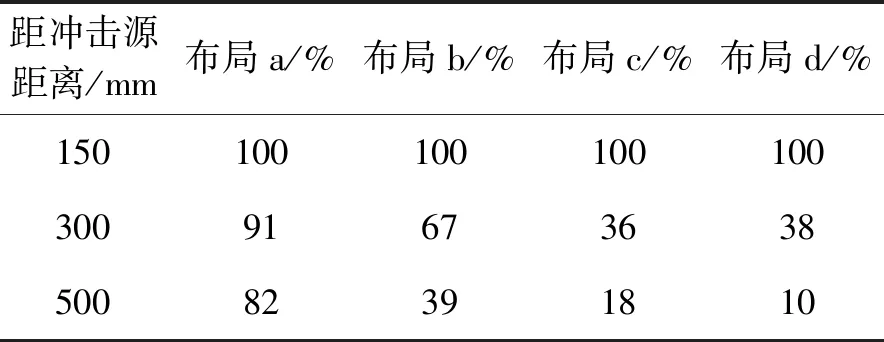
表6 冲击响应衰减情况对比(试验数据)Table 6 Comparison of attenuation of pyroshock response (test)
在工程实际中,由于单机设备质量特性对冲击传递的影响较大,且不同卫星单机设备分布差异较大,因此衰减情况也会存在较大差异,需要结合具体情况进行建模与分析。
3 火工冲击传递特性仿真分析
上文中,通过将火工冲击响应仿真计算结果与试验数据进行对比,验证了冲击有限元建模的合理性。但是仿真分析有限元模型是基于实际卫星型号的布局建立,单机设备的位置及质量特性均已确定,因此无法获得某些具体因素对冲击响应传递的影响规律。
为探究质量大小及质量分布对冲击响应传递的影响规律,基于上述方法对一种常见的简单布局进行有限元建模及分析。在舱板模型上布置一火工品起爆点,距其100 mm处分布有两台单机设备,质量均为m,两者之间的距离为ΔL,计算距火工品起爆点350 mm处的冲击响应。模型布局示意如图10所示,其中黑色正方形为火工品起爆点,长方形为单机设备,黑色三角形为火工冲击响应计算点。

图10 舱板模型布局Fig.10 Layout of satellite board model
当舱板模型上没有单机设备时,经过仿真计算得到距起爆点350 mm处的冲击响应谱最大值为2 156g。当增加单机设备后,计算点处的冲击响应发生变化,本文将以无设备时距起爆点350 mm处的冲击响应为基准,衡量在同一位置处由于设备增加而导致的冲击响应衰减程度,即衰减程度等于同一位置处增加设备后的冲击响应与无设备时冲击响应的比值。
3.1 质量大小对冲击传递的影响
卫星南北板上的大多数单机设备质量分布在5~25 kg范围内,保持两单机设备之间的距离ΔL=100 mm,在此范围内改变单机设备的质量m,计算得到冲击响应衰减程度如图11所示。

图11 质量大小对冲击传递的影响Fig.11 The influence of quality on pyroshock transmission
由图11可得,保持质量分布情况不变,增大单机设备质量时,冲击响应略微减小,但在5~25 kg内,衰减程度均保持在75%~85%之间,计算结果表明在此范围内质量大小的改变对冲击响应传递影响较小。
3.2 质量分布对冲击传递的影响
保持两单机设备的质量m=10 kg,在0~200 mm范围内改变两单机设备之间的距离ΔL,计算得到冲击响应衰减程度如图12所示。
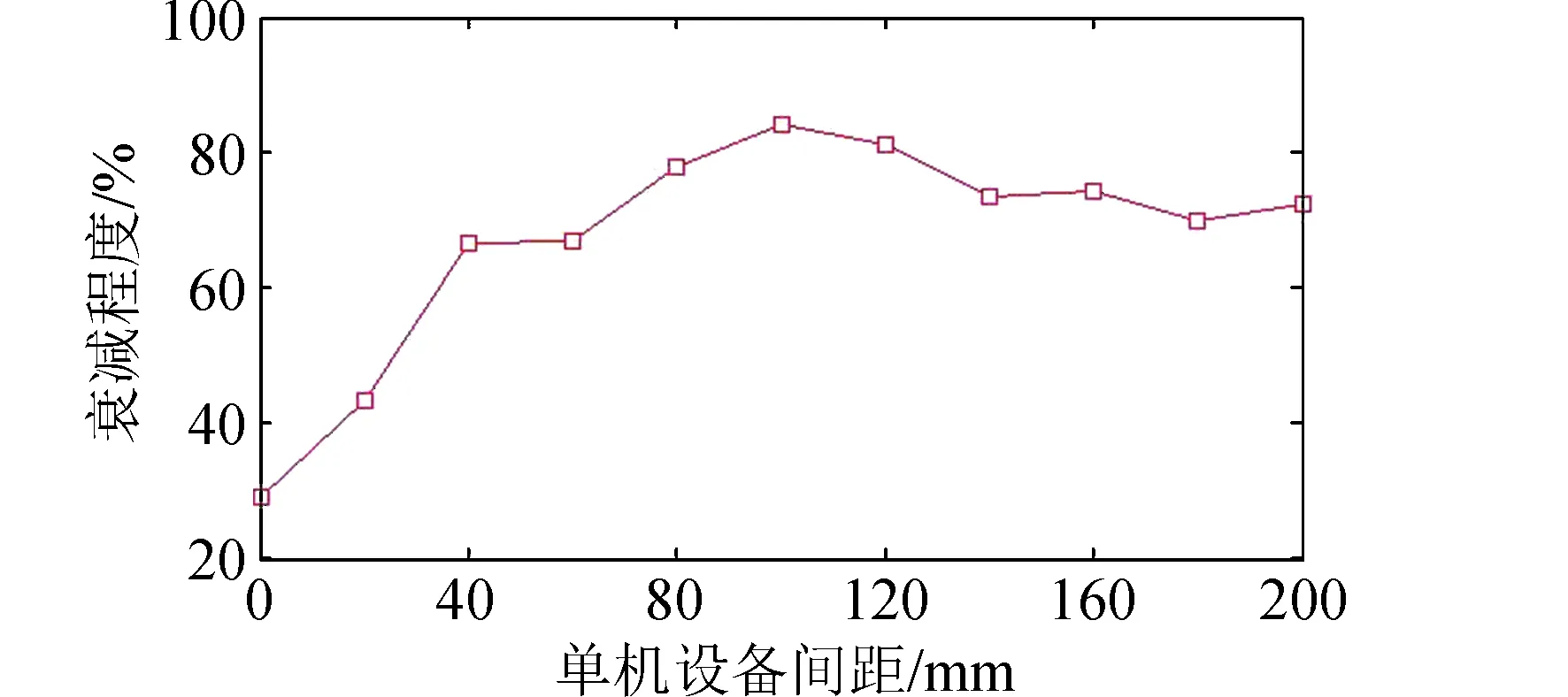
图12 质量分布对冲击传递的影响Fig.12 The influence of quality distributing on pyroshock transmission
由图12可得,保持质量大小不变,当两单机设备间距为零时,计算点的冲击响应仅为无设备分布时的30%;在0~80 mm范围内,随着单机设备间距的增加,冲击响应逐渐增大;当间距大于80 mm后,冲击响应衰减程度保持在70%~80%。由此可得当起爆点与测量点之间有单机设备分布时,冲击响应会大幅衰减,但冲击响应随着间距的增大而逐渐增大,最终保持在一个稳定的范围。
根据上述两方面的对比分析,得到如下结论:在此算例的计算范围内,质量分布对冲击传递的影响大于质量大小对冲击传递的影响。因此在工程实际中应更加注重舱板上单机设备的布局情况。
4 结束语
本文通过对卫星舱板上部分布局特性进行建模与仿真计算分析,计算出了舱板上的冲击响应,并对质量特性对冲击响应传递特性的影响进行了分析,得到以下结论:
1)冲击响应预示结果与试验实测数据误差控制在±3.5 dB以内,验证了有限元建模以及冲击源模拟函数的合理性,可在一定程度上对冲击响应进行预示分析;
2)使用组合脉冲函数可以有效地对火工冲击环境进行模拟,对冲击输入载荷进行了合理的简化,从而进行后续冲击响应预示工作;
3)火工冲击传递特性复杂,质量特性对冲击响应影响较大,可参考此特性对舱板布局进行调整优化;
4)通过算例得出质量特性对冲击响应影响规律的基础是有限元建模的合理性,后续还应进行相关的试验来对结论进行进一步的验证及完善。
