全电推进卫星轨道优化的推力同伦解法

中国空间技术研究院，北京 100094

全电推进(all-electric propulsion)卫星是指不仅在入轨后的位置保持采用电推进技术，而且在火箭与卫星分离后到上升至最终工作轨道的过程也采用电推进变轨的卫星[1]。由于电推进的比冲相比传统化学推进要高近一个量级，因此在相同通信容量的情况下，不配备化学推进系统的全电推进通信卫星的发射质量可以大大减小，或者在相同发射质量的情况下大幅提高有效载荷质量。美国波音卫星系统公司于2015年发射的Boeing 702SP平台是世界上首颗静止轨道全电推进卫星[2]，欧洲空中客车公司制造的全电推进卫星EutelSat 172B也于2017年成功发射[3]。目前世界范围有数十颗全电推进卫星订单，中国也开始了全电推进平台的关键技术研究及平台开发工作[2]。

由于电推进系统的推力非常小，通常只有几十到数百毫牛[4]，从同步转移轨道发射至进入最终静止轨道的过程通常需要几个月到半年的时间[5]，需绕行地球数百圈，此过程中轨道要素和控制量持续周期性波动变化，这也造成其最优轨道求解难度比其它小推力问题更大。

连续小推力变轨是全电推进平台最关键的技术之一，对于连续推力轨迹优化问题的求解，主要可以分为间接法、直接法、混合法，以及状态反馈方法[6-8]。间接法可以获得很高的精度，且寻优变量少，但是协态变量无实际物理意义，对初值猜测准确性要求极高，收敛半径小[6]。直接法对初值要求低，但是寻优变量规模很大，且求解精度比间接法低，容易收敛到局部最优解[6]。混合法结合了间接法和直接法的优点，而状态反馈法采用反馈控制理论，并不是建立在最优控制理论之上，因此只是满足工程要求的简化控制方法。由于间接法对初值猜测的敏感性，使其在全电推进入轨的多圈变轨求解中难以应用，而直接法因多圈转移时间长而存在大量的待优化参数，因此现有的方法主要是通过轨道平均法或状态反馈控制率的方式求解。文献[7]采用了春分点轨道根数平均轨道方程的混合法，完成了地球卫星多圈转移优化。文献[8]提出了基于Lyapunov反馈函数的Q-Law方法，给出了简单实用的反馈控制率，文献[9-10]的方法也可以归为这一类。其中平均法的结果是对多圈取平均得到的轨道要素平根数，无法获取在一圈内的轨道细节信息，而近似反馈控制率不是建立在最优理论之上的，因此其结果距离最优解往往还有较大改进空间，这些方法都无法像间接法那样给出精确的最优解。

在间接法求解燃料最优控制问题方面，文献[11-12]采用同伦思想，取得了很好的效果。同伦方法从容易求解的问题出发，通过迭代的方式逼近难求解的问题。需要指出的是，目前在同伦方法的应用上，现有文献主要是在指标函数上进行渐变，从连续的能量最优问题逐渐逼近到最优的非连续Bang-Bang控制问题，而在时间最优问题方面还少有应用。本文借鉴燃料最优问题中的同伦思想，采用推力逐渐缩小的方式完成间接法求解，可获得全电推进卫星最优时间变轨问题的理论精确解。

1 数学模型

1.1 基于间接法的小推力优化

对于偏心率近似为零的圆轨道，以及近似于零倾角的卫星而言，近地点幅角、升交点赤经将失去意义，此时不宜用传统的轨道六要素来描述卫星的运动，对于静止轨道卫星，可采用春分点轨道根数[13]即 (p,f,g,h,k,L)，其表达式如下：

(1)

式中：a,e,i,Ω,ω,v为经典轨道六要素的半长轴、偏心率、倾角、升交点赤经、近地点幅角和真近点角。

令x=[p,f,g,h,k,L]T，卫星变轨时的推力为T，质量为m，推力器的比冲为Isp，g0为地球海平面加速度，推力方向在轨道的径向、切向、法向这3个方向的余弦为u=[ur,uτ,un]T，则描述卫星运动的微分方程可写为

(2)

(3)

式(2)中的M表达式为[13]:

由于改进春分点轨道根数不如传统轨道根数和直角坐标系那样直观，计算结果需要将改进的春分点轨道根数转换为传统轨道六要素，在三维轨迹作图时需要将改进春分点坐标系到地心赤道惯性系的转换矩阵，这两个计算方法可以参见文献[14]。

依据最优控制理论[15]，对于时间最优指标的最优控制问题，可以构造系统的哈密尔顿函数H如下：

(4)

式中：λ=[λp,λf,λg,λh,λk,λL]为轨道要素的协态变量；λm为质量m的协态变量。根据∂H/∂α=0，可以得到变轨全过程中推力最优控制方向为:

(5)

根据庞特里亚金极值原理，可以得出协态变量[λ,λm]的微分方程如下[15]:

(6)

(7)

式(6)中的∂D/∂x为6×1矩阵，∂M/∂x为6×3×6矩阵，M可依次取Mij，i=1,2,…,6，j=1,2,3，x依次取6个轨道要素。由于元素较多，这里不给出其具体表达式，详见文献[15]。

对于静止轨道全电推进卫星，其最终入轨的轨道根数应满足静止轨道的约束条件，静止轨道半长轴aGEO=42 164 km，则终端约束为:

(8)

式中：tf为转移时间。最优控制问题指标主要有时间最优和燃料最优两种形式。对于全电推进卫星，由于其燃料利用率高，但转移时间非常长，因此宜采用时间最优作为优化目标，即使得J=-tf最大。

1.2 推力同伦求解过程

通过电推进完成静止轨道的入轨过程通常需要数月至半年，由于圈数的增加导致轨道根数呈现振荡变化，增加了间接法协态变量初值的敏感性，降低了猜测值收敛区间[17]。而对微分方程进行长时间、高精度的积分也极大的增加了求解的计算量和计算时间，增加了协态变量初值猜测的难度。为解决这一问题，本文借鉴了小推力轨道燃料最优Bang-Bang问题求解中的一种有效策略，即同伦方法[11-12]，此方法主要用在燃料最优和能量最优两种指标函数之间的渐变，本文利用该思想将其用在时间最优问题的推力大小渐变过程中。

同伦的实质是指从一个简单问题出发，逐渐改变系统的参数，使简单的问题过渡到待求解的一个困难问题。对于最短时间变轨问题，大推力轨道转移的变轨时间更短，协态变量收敛域宽，且积分时间短，求解困难程度将显著降低。对于两个不同推力的最优变轨问题，只要二者对应的推力接近，则可认为二者的协态变量初值也相近，因此稍大推力所求解得到的协态变量精确解可作为初值代入到稍小推力的问题中，这样可以避免直接求解微小推力时的初值猜测的盲目性。

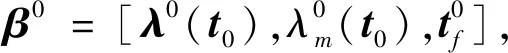
得到β0后，可以以此为初值，逐渐减少推力，完成小推力优化的求解。本文采用推力大小指数缩减的方式完成推力同伦过程，定义大于1的缩减系数s，第j+1次求解时对应推力与第j次的关系为Tj+1=Tj/s。由此构成一个大小递减的系列T0>T1>T2>…>TN，其中TN是要求解的小推力问题对应的推力值，在指数递减过程中如果推力小于TN，则将推力赋值为TN。将β0最为初始猜测值，代入T1对应的优化问题，通过SQP算法迭代后得出T1对应的精确解β1，重复以上步骤，即可获得系列β0，β1，βj，…,βN。其中βN即为最终要求解的小推力问题的协态变量初值。以上过程只要缩减系数s适当，就可以保证每次求解是收敛的。

图1是推力同伦方法求解小推力转移问题的详细流程。

图1 推力同伦求解步骤Fig.1 Flow chart of the thrust homotopic

2 仿真算例

考虑一个从地球同步转移轨道(GTO)到地球静止轨道(GEO)的全电推进转移过程，通过一箭双星方式发射两颗质量各为1 800 kg全电推进通信卫星。每颗卫星依靠两台电推进联合推进，每台的推力230.58 mN，比冲为1 800 s。设星箭分离时卫星轨道根数见表1，目标轨道为GEO轨道，目标轨道的ω以及v均不作约束。

表1 卫星初始和终点轨道要素Table 1 Initial and target orbit elements

使用遗传算法求解初始值，以及SQP求解非线性规划问题需要给出[λ(t0),λm(t0),tf]的上下限，由于协态变量是无量纲单位，主要起作用的是相对大小，因此可以根据经验选取协态变量λ(t0),λm(t0)的上限为100，下限为-100。轨道转移时间tf可根据推力大小和卫星质量，结合脉冲转移速度增量ΔV来进行估算，并适当扩大得出初始的上下限。

SQP算法采用Matlab中fmincon函数，大推力初始猜测值求解过程中带约束遗传算法采用Matlab中GA工具箱完成。推力初始值为50 N，缩减系数s=1.25。经过21次推力缩减过程，求解出了总推力为461.17 mN的最优轨迹，最优飞行时间为109.81 d，消耗工质为247.87 kg。寻优得到的协态变量初值为λ(t0)=[-57.86,8.56,30.12,10.12,40.97,0.07]，λm(t0)=-1.56，最终的a=42 160.82 km，e=0.001 2，i=0.000 33°。

图2是卫星半长轴随时间变化关系，图3是偏心率和轨道倾角随时间变化关系。在增大半长轴的同时，偏心率和轨道倾角随之减少，最终均过渡到目标轨道。

图4是卫星变轨过程三维轨迹图，卫星一共运行约155圈，坐标轴单位是地球半径Re=6 378 km。

图5是推力逐次缩减过程中的λ(t0),λm(t0)最优解。从图5中可以看出，最优解随着推力下降逐渐稳定，尤其是推力缩减5次之后(推力约16N)，λ(t0),λm(t0)波动幅度较小。由此可见，使用前一次求解得到的λ(t0),λm(t0)精确解作为推力缩减一次之后的寻优初始值是合适的。

图2 半长轴变化过程Fig.2 Semimajor-axis vs time

图3 偏心率与倾角变化过程Fig.3 Eccentricity and inclination vs time

图4 卫星变轨轨迹Fig.4 Transfer orbit of the satellite

图5 协态变量初值与推力缩减的关系Fig.5 Initial costate vs thrust reduction times

图6是最优转移时间tf与推力累计缩减倍数之间的关系，转移时间基本与推力缩减倍数呈线性关系。这与常识相符，在推力同伦逐次求解过程中，也可以利用该规律来预计推力缩减一次后的最优转移时间，将s倍tf作为下一次SQP算法中转移时间估计值。

图6 最优转移时间与推力缩减量的关系Fig.6 Minmum transfer time vs thrust reduction

3 结束语

本文采用推力同伦的思想，从比较容易的大推力问题出发，通过逐步减少推力的方式，采用间接法求解了全电推进卫星最短时间入轨优化问题。采用推力同伦的策略大大降低了小推力问题间接法求解过程的初值敏感性问题，可以使问题以较高的概率收敛到最优解。以往多圈转移所采用的轨道平均技术或反馈控制率仅可以获得近似解或平均解，而该方法可提供另一种途径，使得采用间接法求解上百圈小推力转移问题的理论最优解成为可能。

本文的动力学方程是基于二体问题的，后续的进一步研究可以考虑将该方法应用到考虑摄动，地影能源约束等非理性情况下的全电推进卫星入轨优化。