优化学习方式 培养创新意识

王鹄

对小学数学课堂教学而言，基于核心素养下的深度教学是必然趋势。如何通过单元整体教学促进学科能力走向学科素养，从而实现深度教学？

小学是培养学生创新意识和创新能力的关键时期。在小学数学课堂教学中，教师应当把学生的主体地位与作用前置，以独立思考、自主探究、动手实践、合作交流等方式进行深度教学。

一、由“看演示”变为“动手做”

动手操作是帮助学生理解知识、促进求异思维、培养创新意识的重要方式。

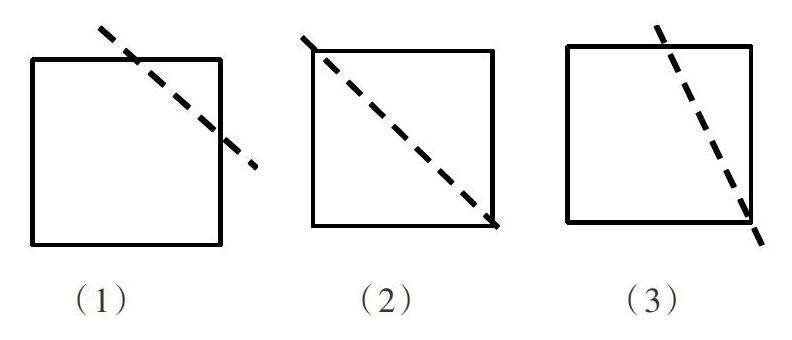
例如：在学生认识四边形的特征后，教师出示一道趣味数学题：“一个正方形，剪掉一个角，还剩几个角？”学生往往会凭直觉把“剪”当作“减”，用4个角减掉1个角得3个角。此时，教師适时提出质疑：“一定剩下3个角吗？”待学生迟疑之时再提示解决方法：“实践出真知。试着剪一剪，看你会有什么发现？”学生通过剪和数，以及组内交流、集体展示，总结出三种的操作方法及相应的结论（如下图）：

第（1）种情况：从相邻两边的中间剪掉一个角，剩下部分变成五边形，所以剩下5个角;第（2）种情况：沿对角线剪，剩下一个直角三角形，所以剩下3个角;第（3）种情况：一端在角的顶点，另一端在对边上，剩下部分是四边形，所以剩下4个角。

这种集动手操作、分析思考、讨论交流、总结提炼等多种方法为一体的深度学习活动，促进了学生思维的发展和创新意识的萌发。

二、由“听讲解”变为“试探究”

教学中，教师要善于满足和利用学生这一心理需求，创设有挑战性的问题情境，把数学问题的探索价值、探索时间和空间留给学生，鼓励学生按照自己的认知能力和思维方式进行多角度地探索。

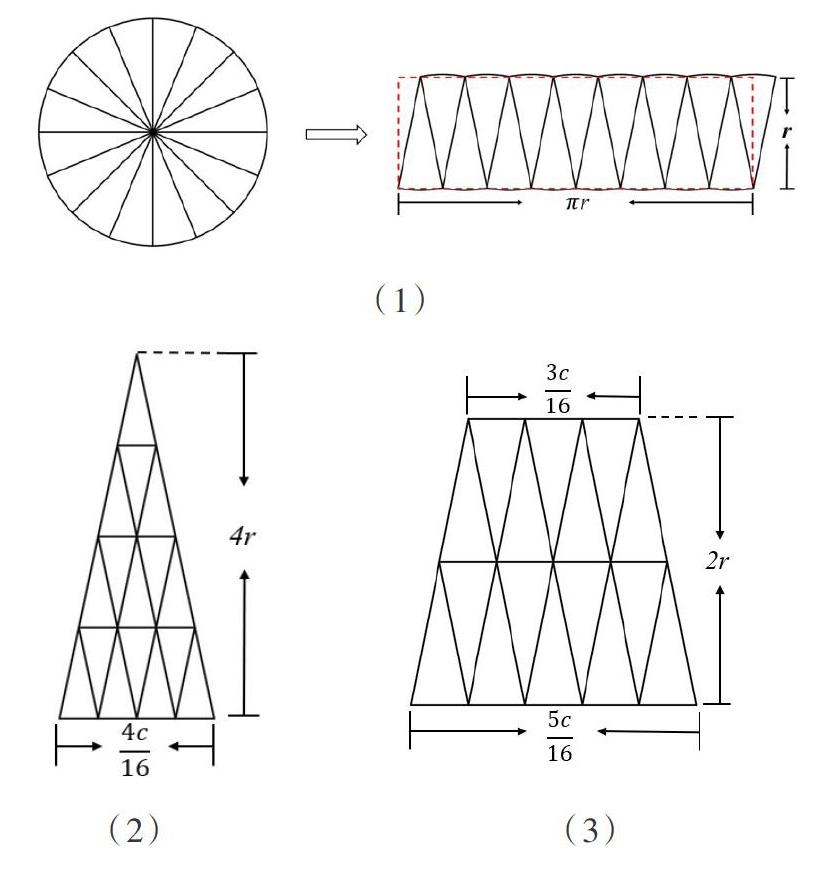
在教学“圆的面积”时，圆的面积计算公式的推导，对于学有余力的学生，不能局限于书本上提出的“把圆等分后拼成近似的长方形”的方法，而要引导学生运用转化的思想，把新知识“曲线图形圆”转化为学过的“由线段围成的多边形”来研究。通过学习单的导学、小组合作的助学，学生理清了圆与转化后的图形之间相关联的量之间的关系，得到以下三种推导方法（如下图）：

（1）近似长方形的长是[π]r，宽是r，根据长方形的面积计算公式可得：S圆=S长=[π]r×r=[π]r2。

（2）近似三角形的底是[4c16=c4]，高是4r，根据三角形的面积计算公式可得： S圆=S三=[12]×[c4]×4r = [12]×[2πr4]×4r=[π]r×r=[π]r2。

（3）近似梯形的上底是[3c16]，下底是[5c16]，高是2r，根据梯形的面积计算公式可得：S圆=S梯=[12]×（[3c16 ]+ [5c16]）×2r=[12]×[c2]×2r=[12×π]r×2r =[π]r2 。

在以上圆的面积计算公式多样化的推导过程中，学生经历了拼组、观察、对比、推理等活动，感悟到转化、推理、极限等数学思想，积累了丰富的活动经验，创新意识也在活动中得到强化。

三、由“口头答”变为“记录单”

用记录单写下思维过程，是一个相对独立和完整的思维活动。它有利于培养学生个性化的思维方法、呈现解题思路。

教学中，教师要借助学习记录单引导学生通过独立或与同桌互助的形式，运用已有的知识和经验自主思考解决问题，并记录下思考过程和结果，内在的思维活动外显化，为展示交流活动提供可视化的素材，促进后续对比、分析、质疑活动的深度开展。

在《分数除以整数》的教学中，学生根据问题情境列出两个不同算式：[45÷]2和[45]×[12]。计算出[45]×[12]=[25]后，教师提出质疑：[45÷]2=[25]吗？[45÷]2和[45]×[12]这个除法算式和乘法算式结果真的完全一样吗？你能否想办法，调动你的数学知识储备，证明一下呢？可以用以前学过的方法算一算，可以借助图形画一画，还可以用手中表示[45]的学习纸折一折。学生经过独立思考，在学习单上记录下自己独特的想法，教师选取并展示了以下几种能代表大部分学生思路的方法：

（1）[45÷]2=[4÷25]= [25]

（2）[45÷]2 （[45]的一半，4÷2=2）=[25]

（3）[45÷]2=（[45]×[12]）÷（2×[12]）=[25][÷1] =[25]

（4）[45÷]2 =0.8÷2 =0.4 =[25]

（5）画：

（6）折：

（7）折：

接下来，教师引导学生观察、比较这些方法，在求同、求异、求联中，深刻理解算理和算法。由学生的质疑“为什么乘[12]”，生长出新知：[ 12]是除数2的倒数;被除数和除数同乘[12]后除数变成1，就把分数除法转换成了分数乘法;分数除以整数，可以直接乘除数的倒数，等等。至此，学生在充分的思维交流、碰撞中，再生出分数除以整数的计算方法，从个性记录、对比展示，再到集体交流，学生思维的独特性、深刻性得以发展。

四、由“独自想”变为“小组议”

在课堂教学中，教师应积极推行小组合作的学习方式，在教学的重点、难点、关键点之处把握时机，组织学生小组合作，让其在合作中解决问题，发展创新意识。

教学“百分数的应用（例5）”时，对于“某种商品4月的价格比3月降了20%，5月的价格比4月又涨了20%，这件商品的价格是涨了还是降了？变化幅度是多少？”这样一个没有提供商品具体价格的数学问题，学生表现出浓厚的探究兴趣。有的学生提出商品3月的价格未知，无法解决;也有学生直接利用“降20%，再涨20%”的信息得出价格不变的结论。

在学生遇到“3月价格未知”的思维障碍之处，教师适时引导学生小组交流解决这一关键问题。学生讨论交流后，知道借助“分数除法”中积累的经验，用“假设法”解决此类问题，可以假设3月价格为具体的数值，可以是抽象的单位“1”，还可以假设为字母a等。有了解题思路，不同层次的学生选择不同的方法验证自己的猜想，变“线型”教学为“板块”教学，有效地保障学生探究的时间与空间。在交流展示环节，学生分享了三种不同方法：

（1）假设此商品3月的价格是100元：100×（1-20%）=100×0.8=80（元），80×（1+20%）=80×1.2=96（元），（100-96）÷100=0.04=4%。

（2）假设此商品3月的价格是单位“1”：1×（1-20%）×（1+20%）=0.96，（1-0.96）÷1=0.04=4%。

（3）假设此商品3月的价格是a元：a×（1-20%）×（1+20%）=0.96a，（a-0.96a）÷a=4%。

在此基础上，教师引导学生进一步讨论：（1）三种不同的方法有什么相同之处？（2）为什么降价和涨价都是20%，商品的价格却发生了变化？（3）如果涨、跌的幅度一致，那么先涨再跌和先跌再涨的结果一样吗？在问题的引领下，学生通过小组讨论交流，不断地探索与思考，掌握了利用假设法解决问题的方法。在此过程中，他们从数学本质上理解了各种假设法的合理性以及内在的一致性，体会变中有不变的思想探究意识和创新意识得以培养。

（作者单位：襄阳市襄州区教研室）