应用型地方高校材料力学的教学方法探讨

陆仁强

摘 要：材料力学是土木工程类专业学生必修的一门专业基础课，也是后续专业课程学习的基础，但是由于其理论的抽象性使得学生在学习过程中存在较大的困难，导致很多学生在学习之初就存在厌学情绪。为此，如何将该门课程的主要内容传授给学生，又要讲解得通俗易懂让学生接受起来容易，就成为地方高校讲授材料力学课程的老师必须解决的问题。笔者通过对材料力学课程的多年讲授，总结了一套简单易懂的教学方法，本文以“扭矩图”的绘制为例，通过例题讲述及结论分析，教学效果反思发现能够让学生很容易的理解该部分内容。

关键词：应用型地方高校;材料力学;扭转;扭矩图

1 圆轴扭转的特点

受力特点：杆两端作用两个大小相等、转向相反的力偶m，且力偶作用面与杆的轴线垂直。

变形特点：杆任意两截面绕轴线发生相对转动。

轴：主要发生扭转变形的杆件，轴一般都是圆截面的，故称为圆轴扭转。

2 扭矩与扭矩图

2.1 扭转内力——扭矩的计算

扭矩：受扭圆轴横截面上的内力，是横截面平面内的力偶，该力偶矩称为扭矩，用T表示，单位：N·m。

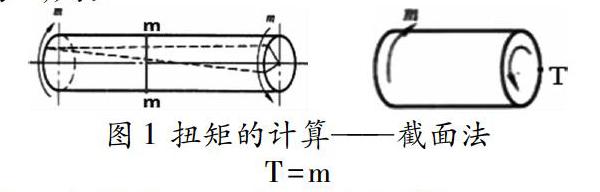
扭矩的计算方法：截面法

如图1所示，圆轴受两个外加力偶矩m的作用产生扭转变形，现求某截面m-m上的扭矩大小，首先采用一个假想的截面将m-m截开，根据左边部分的平衡可知，m-m截面上存在一个扭矩，设为T，则：

T=m

扭矩的正负号规定——右手螺旋法则

用右手握着圆轴，右手的四指指向扭矩T的旋转方向，大拇指代表扭矩的矢量方向，若大拇指指向截面外侧则扭矩为正值“+”，反之为负值“-”。

2.2 扭矩图及其特点

扭矩图：表示扭矩沿圆轴杆件轴线方向变化关系的图形。

控制面：扭矩相同的一段杆的两个端截面，两个相邻分段点之间的杆的扭矩肯定相同，故确定控制面关键是要确定扭矩图的分段点（注：杆件的两个端点、以及在有集中力偶作用处的截面，即为扭矩图的分段点）。

下面通过例题说明扭矩图绘制的基本步骤及具有的特征：

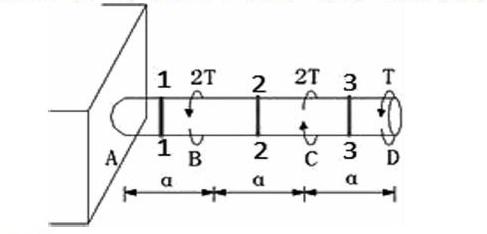
例 某圆轴受力如下图所示，试画出其扭矩图？

主要解答过程：

第一步，确定分段点。

由图可知，A、D为杆件的端点，B、C截面有集中力偶作用，故A、B、C、D均为分段点，四个分段点则可把上述杆件分为三段（AB段、BC段、CD段）;

第二步，分段采用截面法求出每段的扭矩。

求AB段扭矩：

在AB段之间任意取一个截面1-1，利用截面法截开，根据右边杆件部分的平衡，设截面1-1上的扭矩为TAB（通常假设为正），可得：

TAB=2T+T-2T=T（+）

求BC段扭转：

在BC段之间任意取一个截面2-2，利用截面法截开，设截面2-2上的扭矩为TBC，根据右边部分的平衡，可得：TBC=T-2T=-T（—，即2-2截面的扭矩实际方向与假设方向相反）。

求CD段扭矩：

在CD段之间任意取一个截面3-3，利用截面法截开，设截面3-3上的扭矩为TCD，根据右边部分的平衡，可得：

TCD=T（+）

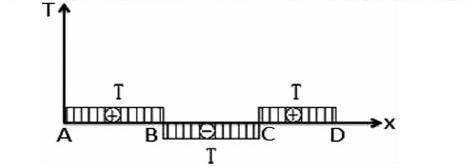
第三步，建立T-x坐标系，画扭矩图。

横坐标为x轴，表示圆轴杆件的轴线方向，纵坐标为T轴（向上为正），表示对应截面的扭矩T，通常取坐标系的原点与杆件的左端点A重合，然后将A、B、C、D四点描在x轴上，并标出AB段、BC段、CD段的扭矩大小，则可得到扭矩图。

3 扭矩图特征分析

以上述扭矩图的B截面进行分析，根据扭矩图可知，B截面为扭矩图的跳跃间断点（称为突变点），其左右极限的差值为|T-（T）|=2T，而根据受力图可知B截面作用的主动力偶恰好为2T;同理，对于C截面，其扭矩图左右极限的差值为|-T-（T）|=2T，而根据受力图可知C截面作用的主动力偶恰好也为2T。

结论（扭矩图的特征）：對于圆轴扭转受集中力偶作用的截面，其扭矩图在该截面处将发生突变，扭矩的突变值等于作用在该截面上的集中力偶。

例 已知变截面传动轴承受外力偶作用如图（a）所示，其扭矩图为图（b），由图（b）可知传动轴B截面处所受的外力偶矩的大小为：（ ）。

（A）2Me （B）3Me （C）5Me （D）Me

解析：由图（b）可知B截面处扭矩左右极限的差值为|3Me-（2Me）|=5M。而扭矩图在某点的突变值就等于该截面上所受的集中力偶M，故答案选C。

4 结论

本文以材料力学课程扭转一章的“扭矩的计算及扭矩图的绘制”为例，通过例题讲解了应用截面法求取扭矩的具体过程，同时提出了扭矩图的绘制方法，更重要的是通过对扭矩图的分析，结合外部荷载与扭矩之间的关系，得到了扭矩图变化的一些特征。该教学方法通俗易懂，没有太多的理论讲授，将理论贯穿于例题讲解的过程中，学生听起来不觉得枯燥乏味，也简单易懂。

参考文献：

[1]严岩.“材料科学前沿”课程教学革新与探索[J].西南师范大学学报（自然科学版），2016（05）.

[2]彭细荣.基于创新项目的材料力学教学中能力培养探索[J].教育教学论坛，2015（50）.