昆明盆地泥炭质土动力学参数统计研究*

文 雯，虎雄林，毛先进，隋明坤，王林建

(云南省地震局，云南 昆明 650224)

0 引言

土的动力特性是指土体在动力作用下所反应的工程性质。由于土是一种非连续介质，当土受到地震、海浪冲击、机械振动等振动影响时，在土中的传播就不再是谐振，而是一种振动能量和振幅都随时间而减小的阻尼振动。20世纪，我国开创了用动三轴试验进行土动力学研究的新途径(谢定义，2007)，通过对土类取原状样，使用共振柱仪、扭剪仪、动三轴仪等，试验测试不同土类动剪切模量比与剪应变，阻尼比与剪应变的变化曲线。这种变化曲线可以用来描述土体在一系列特殊作用下的本构关系。动剪切模量表示材料在动荷载作用下所表现出来的弹性性能参数，其数值越大，表明材料的弹性承载性能越好；而阻尼比的大小可以用来表示振幅衰减的快慢，阻尼比越大，振幅衰减得越快。动剪切模量比与阻尼比是表征场地条件及其土类性质的重要参数之一，也是土层反应分析和工程场地地震安全性评价工作中不可或缺的参数。这2个参数的选取是否合理，影响着工程建筑结构的安全性和合理性。

对特定区域尤其是国内主要大中城市土层的动力学参数进行研究，有助于提高对区域地下土层结构的认识，并研究土层模型对地表地震动的影响，对提高该地区的抗震设防能力有很重要的工程意义和社会价值。目前，前人对国内一些主要城市土层的动力学参数的研究，已取得一些有价值的研究成果，如施春花等(2009)对北京地区粉质黏土土动力学参数进行了统计分析；夏峰等(2015)对天津地区覆盖层土动力学参数进行了统计分析；孔宇阳等(2014)对武汉地区典型土类动力非线性参数进行了统计分析，以上研究表明，由于土的类型、形成时代及沉积环境的不同，土动力学参数具有明显的区域性特征。

昆明盆地为晚新生代以来形成的断陷盆地，盆地内除东部有低矮山丘零星分布外，大部分地势平坦(黄发政等，1984)。受高原气候和湖相沉积环境作用，泥炭质土在昆明盆地有广泛的分布。泥炭质土是由已分解的腐殖质、尚未完全分解的植物残体及矿物质组成的一种特殊土，其含水率高、孔隙比大、天然密度小、有机质含量高、工程性质较差。对泥炭质土动力特性的研究已受到许多学者的重视，如丁祖德等(2016，2017)利用动三轴仪对昆明某工地6.0～6.2 m的泥炭质土样进行了动力试验，并将得到的泥炭质土的动剪切模量比和阻尼比与不同地区泥炭质土、一般黏性土的动剪切模量、阻尼比进行了对比分析。但已有研究中，泥炭质土取土深度和数量均有限，难以代表不同埋深范围内泥炭质土的动力特性。本文收集了近年来昆明盆地泥炭质土土样的动三轴报告，使用取平均值的方法，得到昆明盆地不同埋深区间的泥炭质土土动力学参数结果，再选取昆明盆地内不同埋深的2个钻孔，分别输入钻孔实测值和本文得到的统计值，以及不同概率水准的人工合成地震动，进行一维土层反应分析计算，分析统计值的适宜性。

1 数据统计分析

1.1 数据选取

近年来，由于地铁、高层建筑以及其他一些新建、改扩建工程的需要，昆明盆地内开展了许多地震安全性评价工作，实测了大量的土动力学参数试验数据。本文选取昆明盆地内埋深为0～100 m的62个取样点的128组泥炭质土样的动三轴实验数据开展研究。这些数据均来自于云南省地震工程勘察院动三轴实验室，试验仪器为北京市新技术研究所生产的DDS-70微机控制电磁式多功能静动三轴试验系统。所选数据数量丰富，分布较为均匀，且具有地域代表性(图1)，并避免了由于实验室，以及实验仪器和方法、实验条件、数据分析等不同造成的数据差异。

1.2 泥炭质土的土动力学参数统计值

由于同类土体的土动力学参数随埋深和围压的变化而有所不同，选取不同埋深区间进行数据统计是可行且有意义的(孔宇阳等，2014)。考虑到覆盖层厚度在0～30 m时对土层地震反应的结果最为敏感(文雯等，2012)，在埋深区间的划分上综合考虑2个原则：① 0～30 m范围内尽量细分，但须保证分区内样本量不能太少；② 尽量使样本数据平均落于各埋深分区内。统计不同埋深区间泥炭质土样本量分布及分组，见表1。

在进行统计计算时，采用取平均值的计算方法，删除了差异较大或较小的样本数据，以保证样本具有代表性，用标准差保证数据不至于太过离散。表2为不同埋深区间泥炭质土的统计平均值。由表2可知，动剪切模量比的标准差最大值小于0.15，阻尼比的标准差最大值小于0.06。

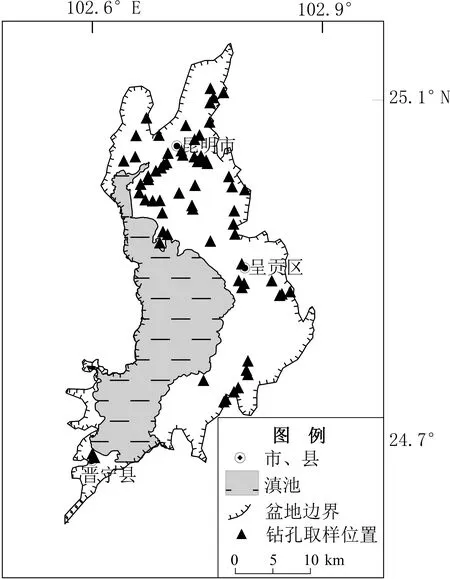
图1 昆明盆地泥炭质土取样点分布图Fig.1 Distribution map of engineering sites of peaty soil in the Kunming basin

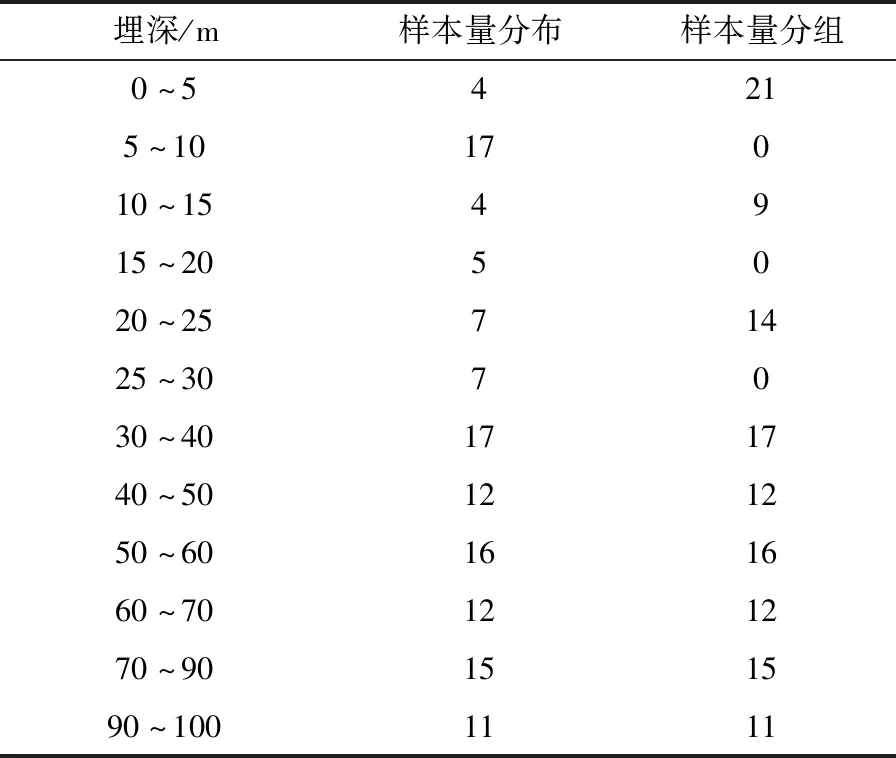
表1 不同埋深区间泥炭质土样本量分布及分组Tab.1 Total sample numbers and groups of the peaty soil at different depth ranges

1.3 泥炭质土统计值的埋深特征

图2为不同埋深区间泥炭质土的动剪切模量比、阻尼比随剪应变的变化曲线。从图中可以看出，同一埋深区间，随着剪应变值的增大，动剪切模量比呈逐渐减小、阻尼比呈逐渐增大的趋势。当剪应变较小时，各埋深区间动剪切模量比和阻尼比的变化均不大；当剪应变较大时，各埋深区间剪切模量比和阻尼比的差异变大。

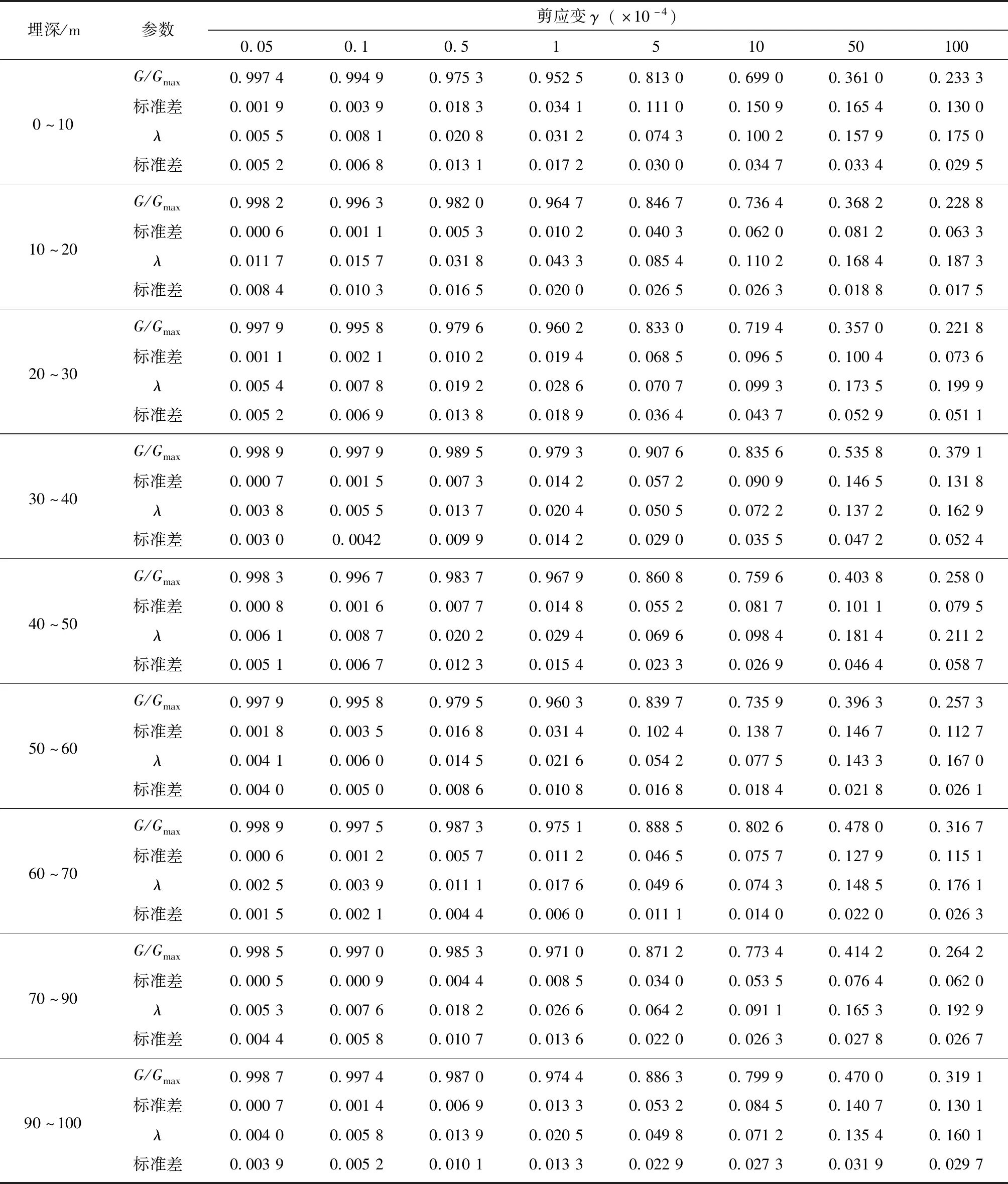
表2 不同埋深区间泥炭质土的统计平均值Tab.2 The mean values of dynamic parameters of the peaty soil at different depth ranges

图3为不同剪应变下泥炭质土动剪切模量比随埋深的变化曲线，由图可见，剪应变相同时，随埋深的加深动剪切模量比的分布并不规则。但不同剪应变的埋深-动剪切模量比曲线形状较为相似，且动剪切模量比均在30～40 m达到最大值；最小值对应的埋深区间略有差异：剪应变为5.0×10-6～1.0×10-3时，动剪切模量比的最小值对应的埋深区间相同，为0～10 m(图3a～f)；剪应变为5.0×10-3和1.0×10-2时，动剪切模量比最小值出现在20～30 m(图3g～h)。

图4为不同剪应变下泥炭质土阻尼比随埋深的变化关系曲线。从图中可见，随埋深的加深阻尼比的分布也不规则。当剪应变为5.0×10-6～5.0×10-4时，泥炭质土阻尼比-埋深曲线形状较为相似，阻尼比最大值出现在10～20 m，最小值出现在60～70 m(图4a～e)；剪应变为1.0×10-3时，阻尼比最大值出现在10～20 m，最小值出现在30～40 m(图4f)；剪应变为5.0×10-3～1.0×10-2时，阻尼比-埋深曲线形状较为相似，阻尼比最大值出现在40～50 m，最小值出现在30～40 m(图4g～h)；各曲线呈现出随着剪应变的增加，阻尼比最大值对应的埋深逐渐变深，最小值对应的埋深逐渐变浅的特点。

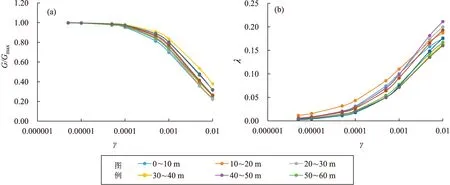
图2 不同埋深区间泥炭质土动剪切模量比(a)、阻尼比(b)变化曲线Fig.2 The diagrams of dynamic shear modulus ratio(a)，damping ratio(b) of the peaty soil at different depth ranges

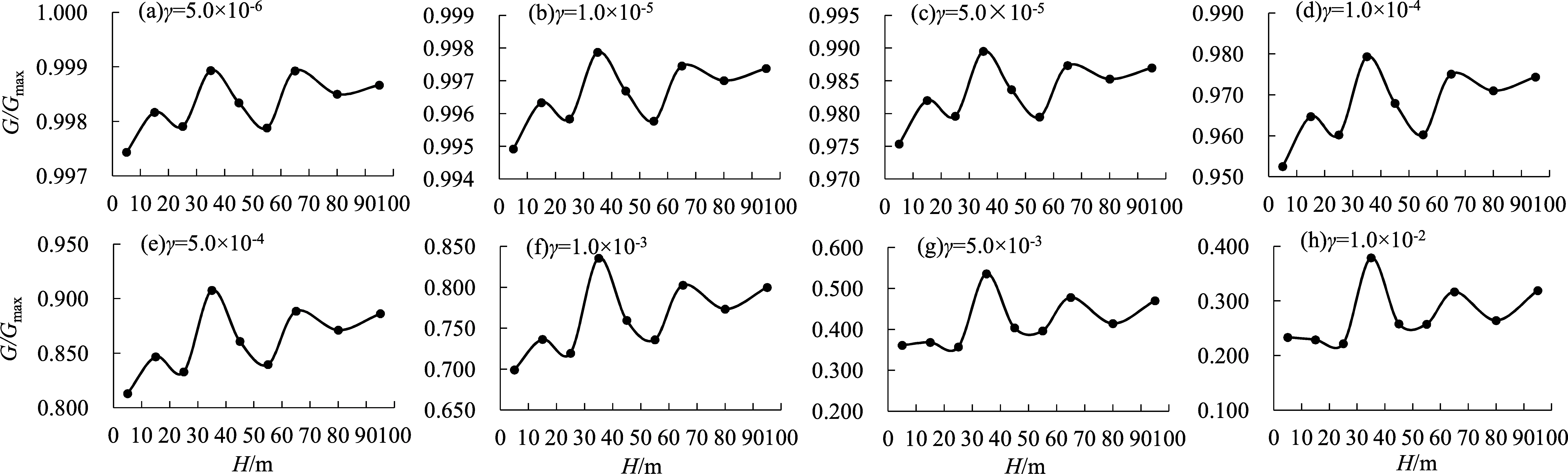
图3 不同剪应变下泥炭质土动剪切模量比随埋深的变化图Fig.3 The diagram of shear modulus ratio of the peaty soil varying with depth

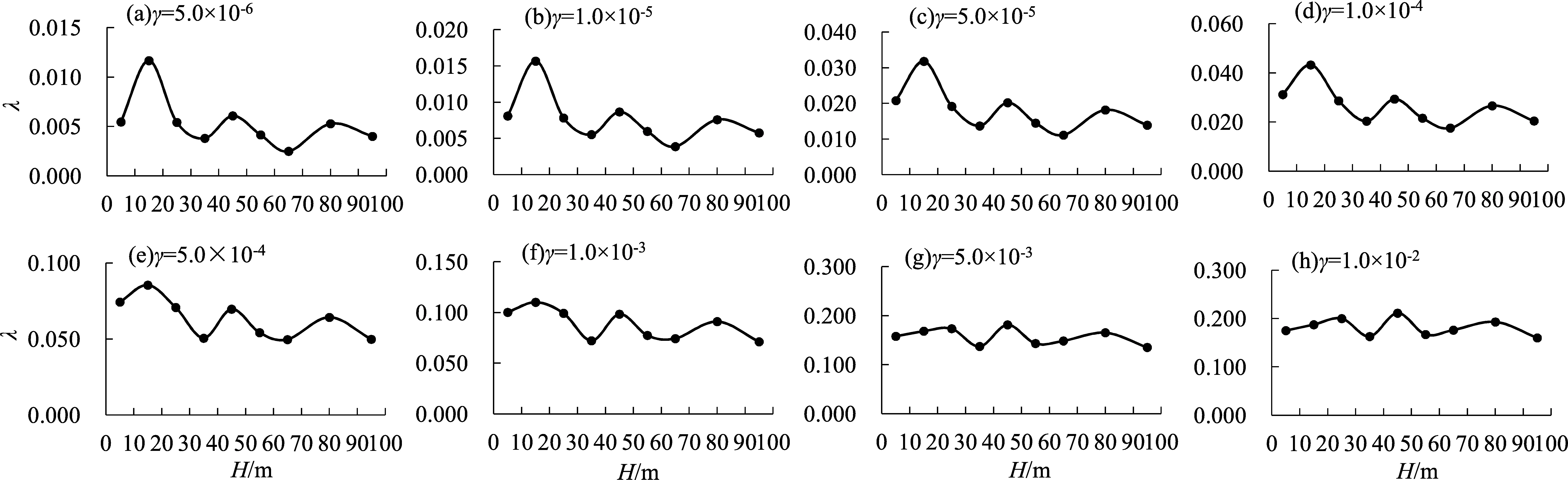
图4 不同剪应变下泥炭质土阻尼比随埋深的变化图Fig.4 The diagrams of damping ratio of the peaty soil varying with depth

1.4 泥炭质土统计值与黏土统计值对比分析

在以往的地震安全性评价工作中，当现场工作取样困难，得不到土类原状样进行动三轴试验时，通常会参考基于试验数据得到的规范值或推荐值。《工程场地地震安全性评价工作规范》(DB001—94)给出的规范值(下文简称“94规范”)和袁晓铭等(2000)给出的推荐值是应用较为广泛的参考数据，但是，94规范和袁晓铭等(2000)推荐值均并没有给出泥炭质土的土动力学参数统计结果。目前，还没有昆明盆地泥炭质土动力学参数统计结果。因此，将本文得到的泥炭质土统计值分别与94规范给出的黏土、粉质黏土、淤泥质黏土动力学参数统计值进行了比较，如图5所示。

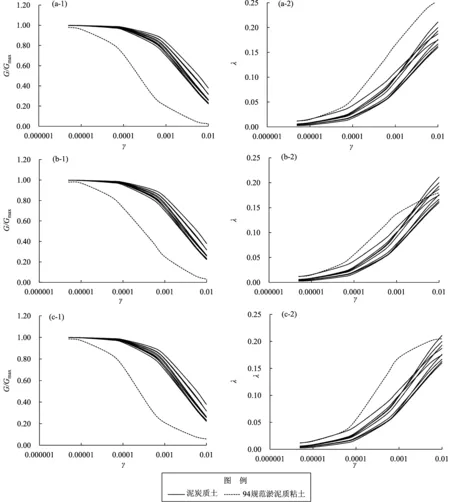
图5 泥炭质土统计值分别与94规范给出的黏土(a)、粉质黏土(b)、及淤泥质黏土(c)的土动力学参数对比曲线Fig.5 Relationship of soil dynamic parameters between the peat soil and clay(a)， silt clay(b)，and muddy soil(c)

由图5a可看出，昆明盆地的泥炭质土和94规范黏土的动剪切模量比、阻尼比变化曲线均有较大差异。泥炭质土的动剪切模量比明显大于94规范黏土，阻尼比明显小于94规范黏土，这说明在动荷载作用下，泥炭质土的弹性承载性能稳定程度较94规范黏土好，振幅衰减较94规范黏土慢。

由图5b可看出，泥炭质土的动剪切模量比明显比94规范粉质黏土大；当剪应变小于5.0×10-5时，94规范粉质黏土的阻尼比略大于泥炭质土的阻尼比；当剪应变为5.0×10-5～1.0×10-3时，两者之间的差异逐渐变大，且在剪应变为1.0×10-3时，差异达到最大。当剪应变为5.0×10-2时，94规范粉质黏土与泥炭质土的阻尼比曲线相交，这说明在动荷载作用下，泥炭质土的弹性承载性能稳定程度较94规范粉质黏土好；当剪应变小于5.0×10-2时，泥炭质土振幅衰减较94规范粉质黏土慢；当剪应变大于5.0×10-2时，部分埋深处的泥炭质土与粉质黏土振幅衰减相差不多。

由图5c可看出，泥炭质土的动剪切模量比明显比94规范淤泥质黏土的大。当剪应变小于1.0×10-4时，94规范淤泥质黏土的阻尼比略大于泥炭质土的阻尼比；当剪应变为1.0×10-4～1.0×10-3时，两者之间的差异渐渐变大，且在剪应变为1.0×10-3时，达到最大；当剪应变大于1.0×10-3时，94规范淤泥质黏土阻尼比渐渐趋向于泥炭质土的阻尼比。这说明在动荷载作用下，泥炭质土的弹性承载性能稳定程度较94规范淤泥质黏土好，泥炭质土振幅衰减较94规范淤泥质黏土慢。

2 泥炭质土动力学参数统计值适用性分析

为了分析本文得到的泥炭质土动力学参数统计值的适用性，选取昆明盆地内不同埋深的2个钻孔、选择5种方案，分别输入94规范给出的黏土值、粉质黏土值、淤泥质黏土值，钻孔取样的泥炭质土实测值以及本文的泥炭质土统计值，采用一维等效线性波动法，进行土层反应计算，并分析其计算结果。

2.1 场地模型及参数确定

在昆明盆地内选取的2个典型钻孔的覆盖层厚度分别为84.7和52.1 m，所揭示地层主要为泥炭质土和粉质黏土，其层底深度、分层厚度、剪切波速、密度均为实测值，钻孔模型见表3，4。

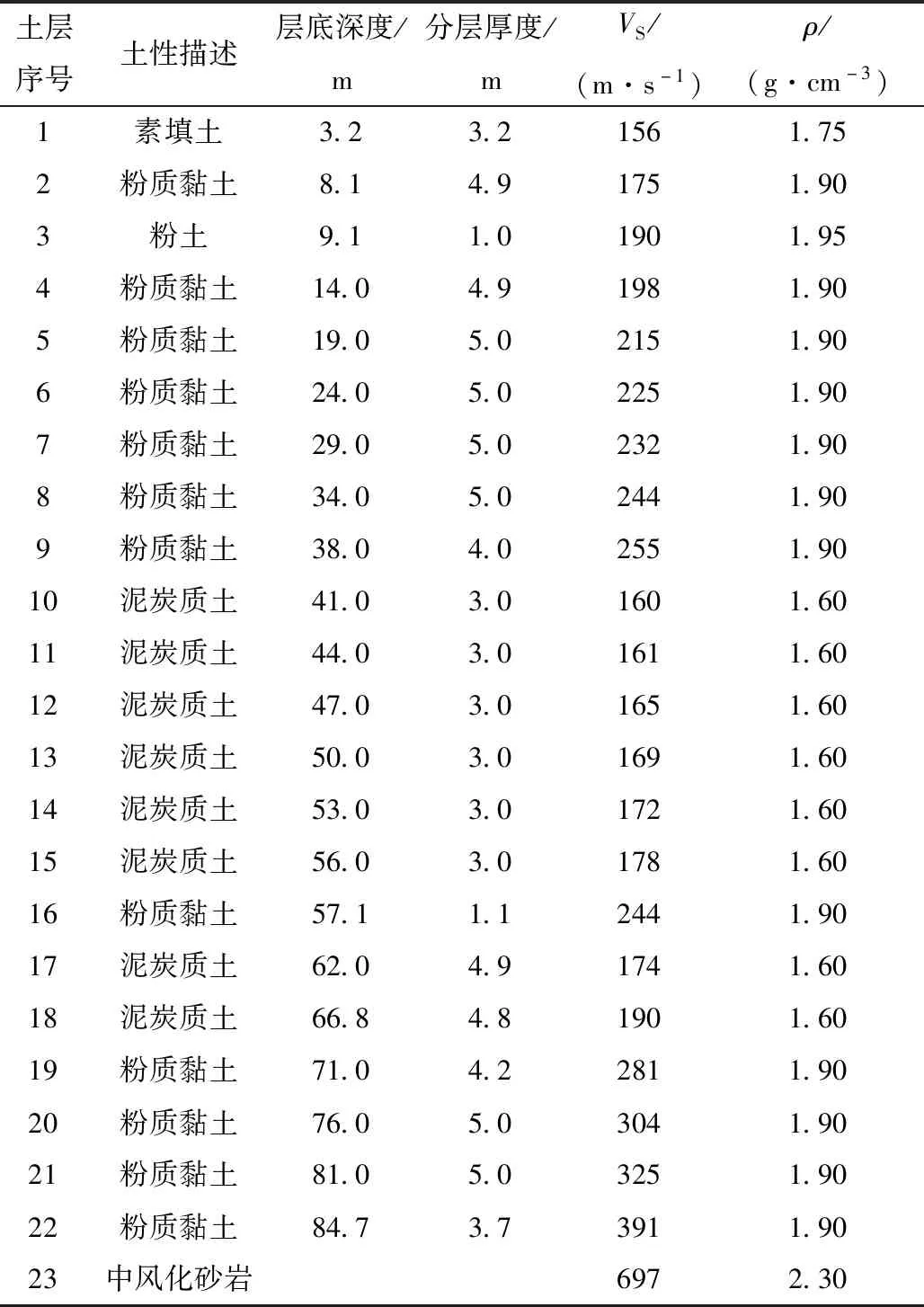
表3 场地模型1土层剖面参数Tab.3 Soil profile parameters of the site model 1

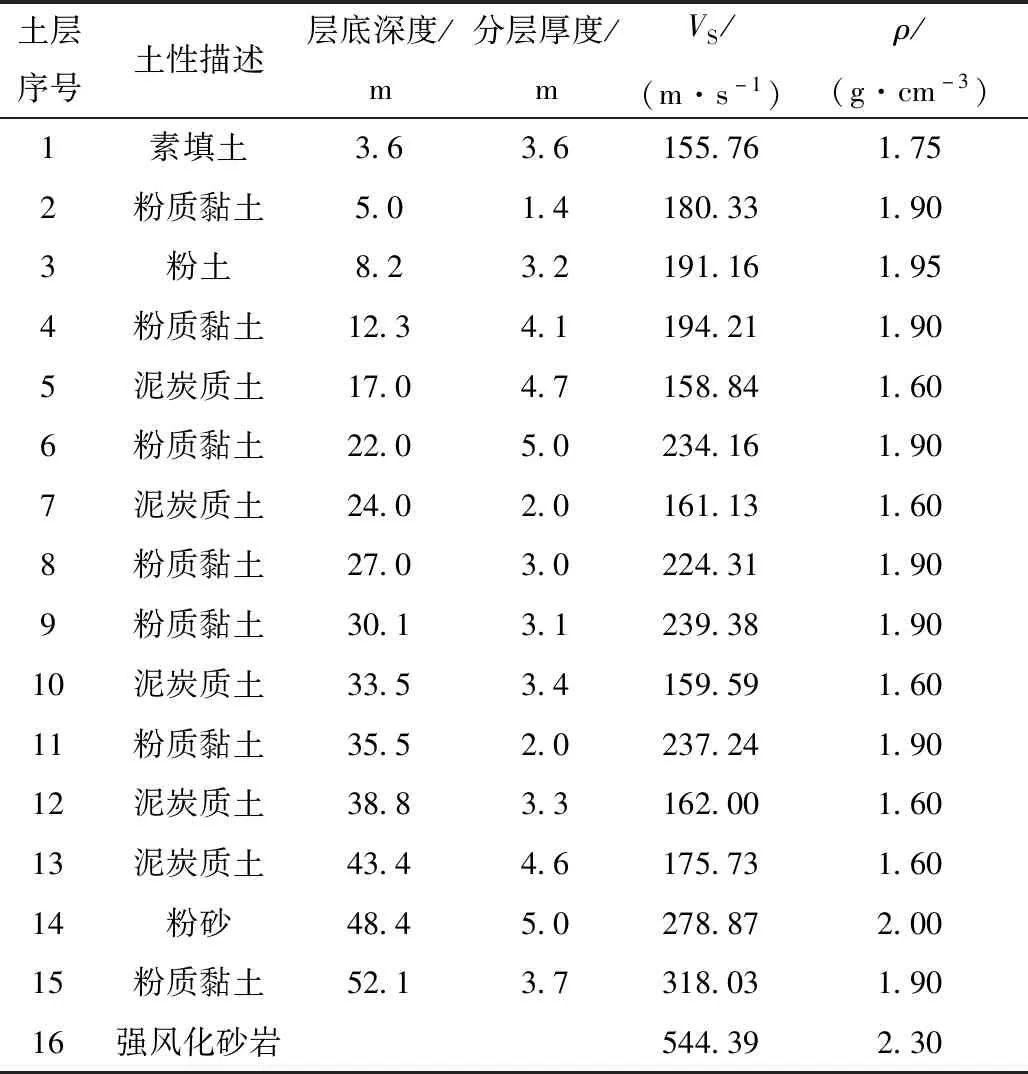
表4 场地模型2土层剖面参数Tab.4 Soil profile parameters of the site model 2

2.2 输入地震动

在合成基岩输入地震动时，选取选场地地震危险性分析得到的结果作为50年超越概率63%，10%和2%所对应的目标加速度峰值和反应谱(图6)。50年超越概率63%，10%，2%的基岩加速度峰值分别为 69.4，201.7，340.2 gal。为了考虑随机相位的影响，每个概率水准都合成3个不同随机相位的地震动时程样本。合成的时程均以0.02 s为间隔，其离散点数为2 048或4 096。在合成过程中，利用逐步逼近目标谱的方法，使合成的加速度时程谱近似满足目标谱，拟合相对误差小于5%。

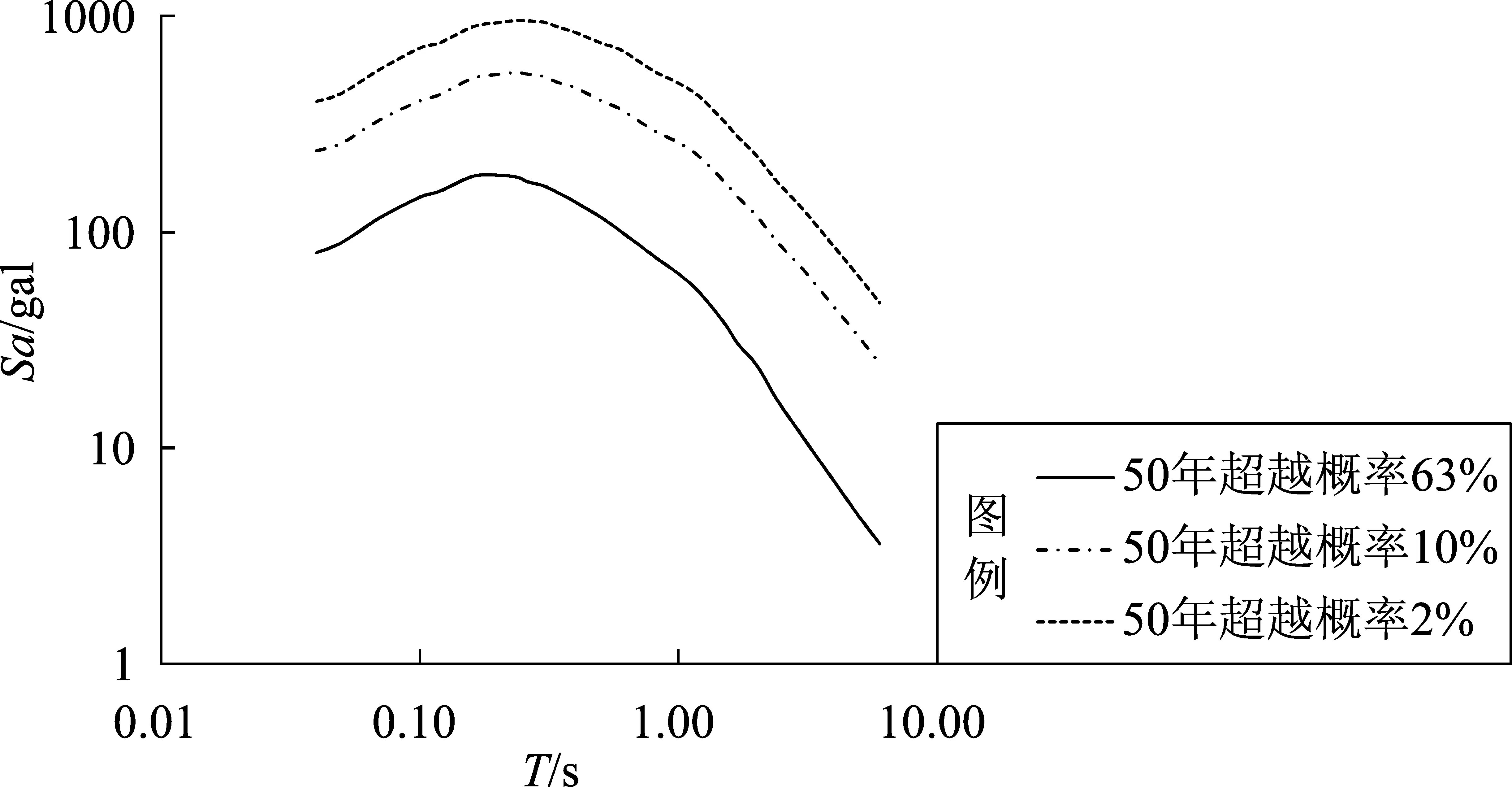
图6 场地基岩不同超越概率反应谱Fig.6 Site rock response spectrum curves with different exceedance probabilities

2.3 峰值加速度结果分析

通过土层反应分析，计算得到2种场地模型在50年超越概率63%，10%和2%的3个随机相位的峰值加速度(表5)。从表5可见，2种模型中使用94规范黏土值、粉质黏土值、淤泥质黏土值计算得到的3种概率峰值加速度均小于实测值。

由表6可见，模型1中使用94规范黏土值、粉质黏土值、淤泥质黏土值与实测值计算得到的概率峰值加速度最大偏差为-91.1%，最小偏差为-43.1%；模型2中使用94规范黏土值、粉质黏土值、淤泥质黏土值与实测值计算得到的峰值加速度最大偏差为-84.2%，最小偏差为-47.9%。因此，实际工作中，若选用94规范中的这3种土类替换泥炭质土的动力学参数值，存在地表峰值加速度被低估的风险。

由泥炭质土的实测值与统计值得到的峰值加速度计算结果差异较小，从不同的概率水准上看：50年超越概率63%水准下，泥炭质土实测值与统计值得到的峰值加速度的差异最小；50年超越概率10%水准下，实测值与统计值之间的差异次之；50年超越概率2%水准下，实测值与统计值之间的差异较前两者大，场地模型1，2使用实测值与统计值计算得到的结果偏差最大分别为-10.3%和9.1%。

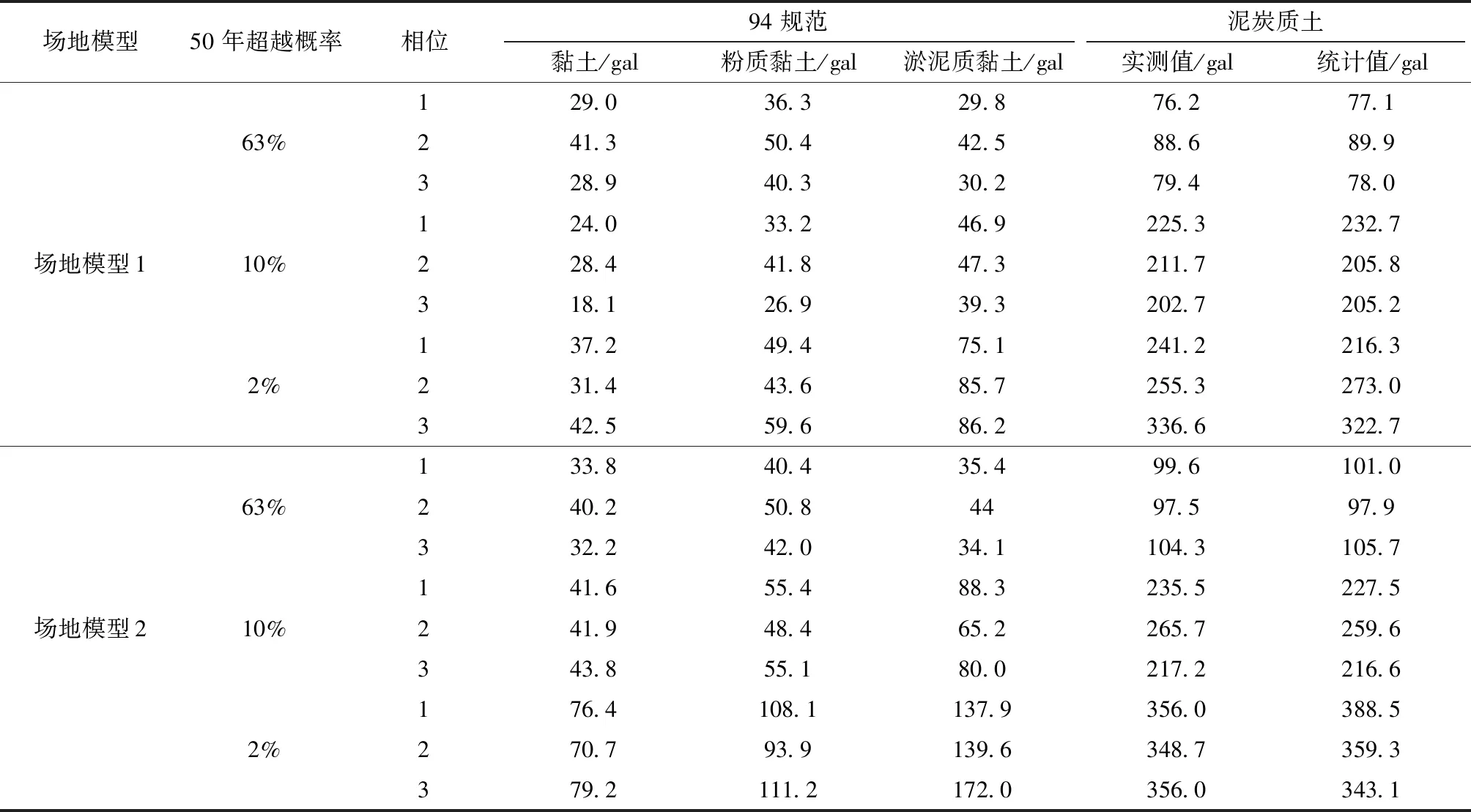
表5 场地模型1和模型2概率峰值加速度结果Tab.5 The peak ground acceleration of the site model 1 and model 2

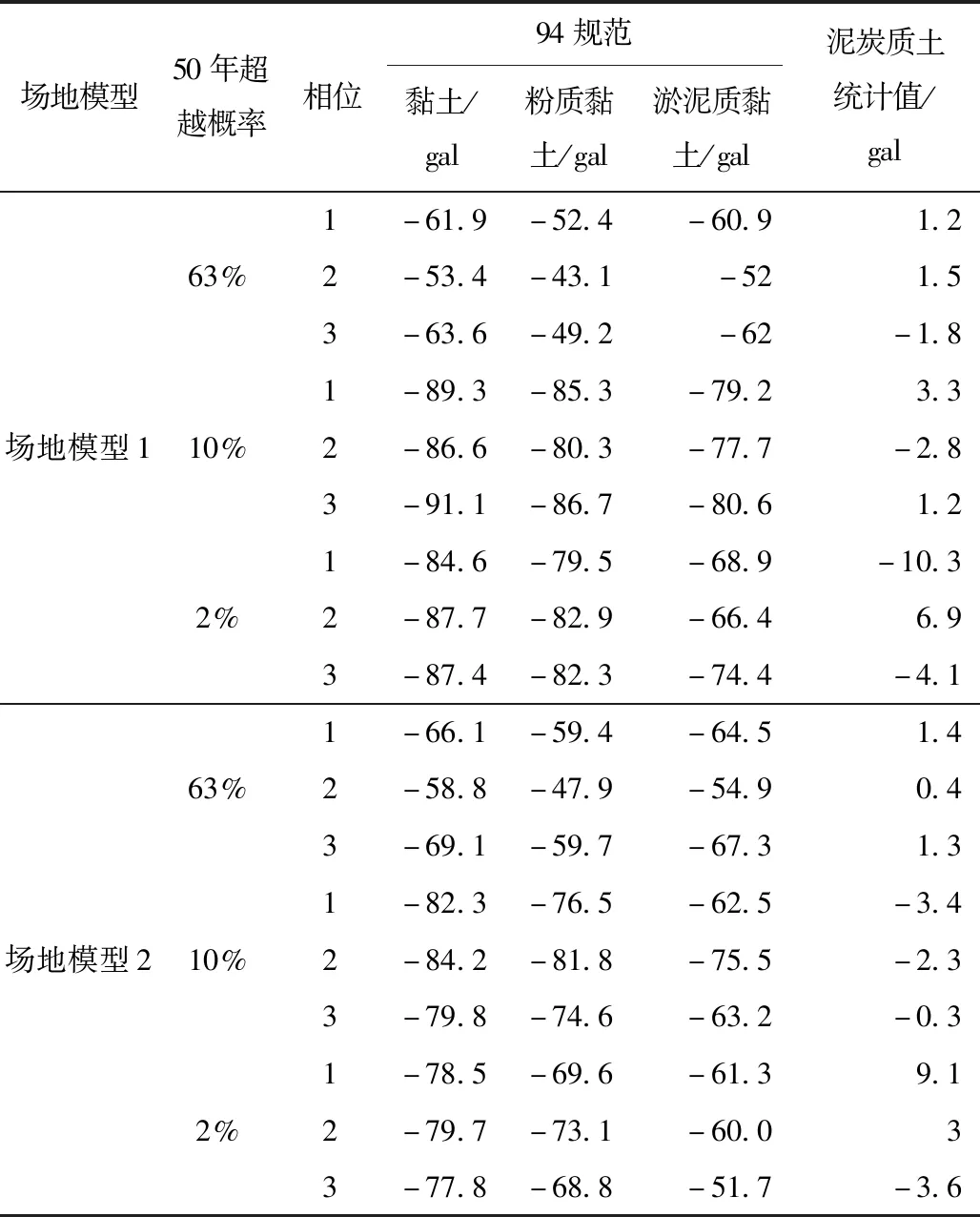
表6 4种土动力学参数取值与实测值所得峰值加速度结果的偏差(%)Tab.6 Deviation of peak ground acceleration between 4 schemes of soil dynamic parameters(%)

2.4 加速度反应谱结果分析

分别输入泥炭质土的实测值与统计值进行土层地震反应，计算得到场地模型1和模型2的加速度反应谱。从图7可以看出，同一场地模型中，由94规范黏土值、粉质黏土值、淤泥质黏土值计算得到的加速度反应谱峰值较小，反应谱平台偏低，谱型较宽，与实测值计算得到的反应谱差异较大。场地模型1中，将泥炭质土实测值与统计值计算得到的加速度反应谱相比发现，50年超越概率63%的反应谱形状基本重合，50年超越概率10%的反应谱形状差异次之，50年超越概率2%的反应谱形状较前二者略大。场地模型2中，将泥炭质土实测值与统计值计算得到的反应谱相比发现，50年超越概率63%和2%的反应谱形状基本重合，50年超越概率10%的反应谱形状稍有差异。总体来说，由泥炭质土实测值与统计值计算得到的反应谱形状基本相似。

3 结论

本文统计了近年来昆明盆地内泥炭质土的动力学参数，分析了剪切模量比和阻尼比随深度的分布情况。将统计得到的泥炭质土统计值与94规范给出的黏土、粉质黏土、淤泥质黏土的土动力学参数统计值进行了对比分析，再在昆明盆地内选取了2个不同埋深的钻孔，输入94规范值黏土值、粉质黏土值、淤泥质黏土值、泥炭质土实测值和统计值，以及50年超越概率63%，10%，2%的人工合成地震动进行土层反应计算，结果表明：

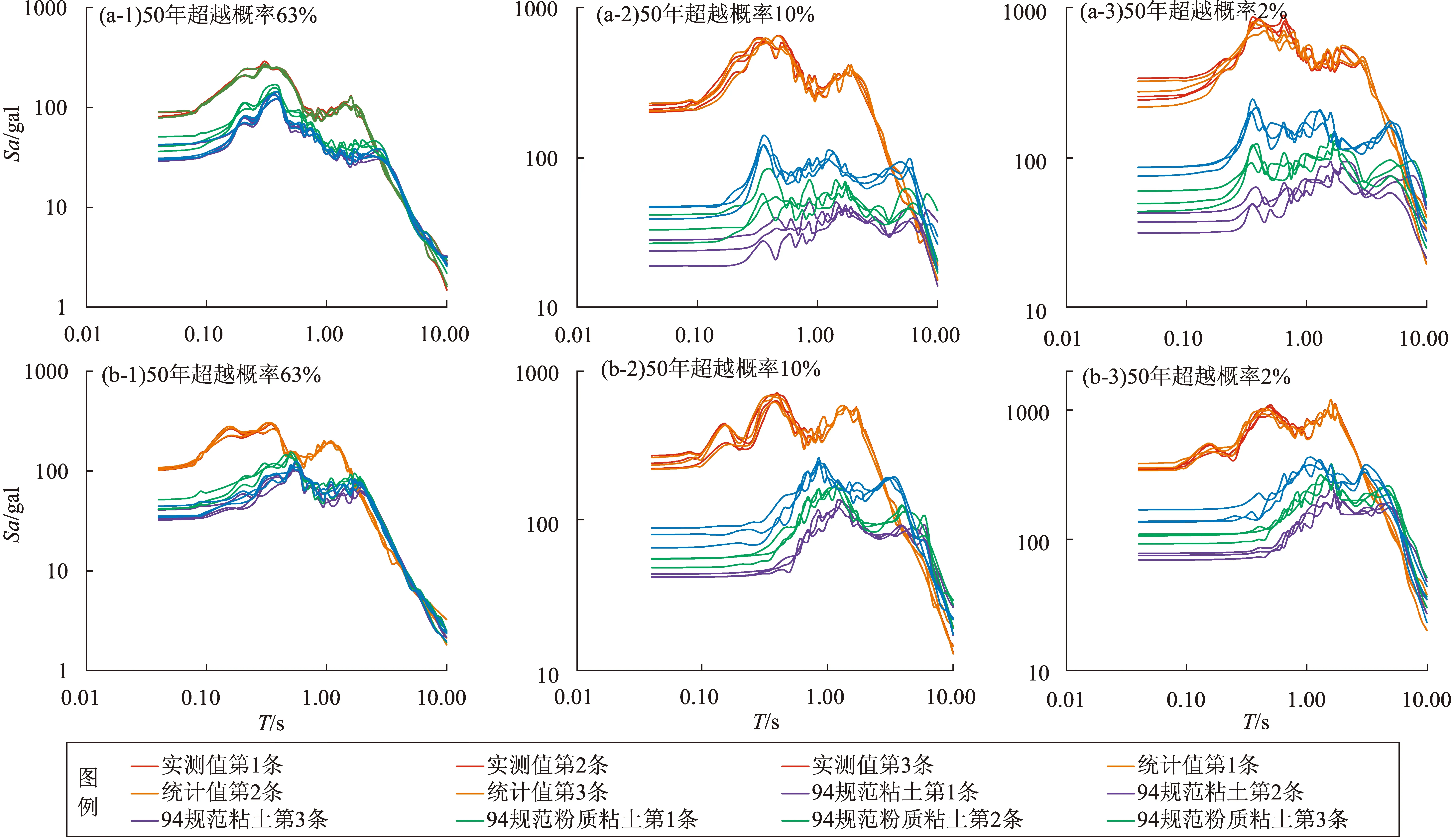
图7 场地模型1(a)和模型2(b)地表50年3种概率加速度反应谱Fig.7 The horizontal acceleration response spectrum curves of site model 1 and model 2

(1)统计得到的泥炭质土动剪切模量比随埋深的分布情况为：剪应变相同时，动剪切模量比的分布随埋深加深的变化并不规则；不同剪应变的埋深-动剪切模量比曲线形状较为相似，剪切模量比均在30～40 m达到最大值，而最小值对应的埋深区间略有差异。

(2)统计得到的泥炭质土阻尼比随埋深的分布情况为：剪应变相同时，阻尼比的分布随埋深加深的变化也不规则；不同剪应变的埋深-阻尼比曲线相比，各曲线的最大值对应的埋深有随着剪应变的增加变深的特点，各曲线的最小值对应的埋深有随着剪应变的增加变浅的特点。

(3)94规范给出的黏土值、粉质黏土值、淤泥质黏土值计算得到的峰值加速度均小于泥炭质土实测值所得到的峰值加速度。94规范给出的黏土值、粉质黏土值、淤泥质黏土值计算得到的加速度反应谱与泥炭质土实测值计算得到的加速度反应谱差异较大。实际工作中，若选用上述3种土类94规范值替换泥炭质土的动力学参数值，存在地表峰值加速度被低估，且给出的地表反应谱不能反映场地特性的风险。

(4)实测值与统计值计算得到的不同概率水准的峰值加速度和反应谱均差异不大。当现场工作取样困难，得不到可供试验的原状样时，可考虑选择使用本文的统计值。