自适应响应面法在电池包尺寸优化研究中的应用

刘嘉楠，徐 宽，张洪杰，王金荣，王海龙，许 强

（河北钢铁集团唐山钢铁有限责任公司，河北唐山 063000）

0 引言

随着全球环境形势的日益严峻，如何更好地节能减排成为了当前汽车工业面临的主要问题。有数据表明，新能源汽车质量每降低10 kg，续航里程可增加2.5 km。在严苛的节能降耗法规下，零部件的轻量化将成为新能源车企实现低碳、环保目标的主要途径。轻量化结构设计方法主要有拓扑优化、形貌优化、形状优化、尺寸优化等[1]。尺寸优化是发展比较成熟的一种参数化优化方法，主要是通过参数调节，如改变壳单元的厚度、梁的横截面参数等，达到改善结构特性的目的，如降低设计重量、减小应力等。

作为新能源汽车的动力源，电池包是电动汽车的心脏部件，其结构强度关系到电池的正常使用安全。作为评价电池包在颠簸路况、极限载荷下的结构强度，机械冲击在电池包的安全法规标准中是一项重要测试内容。它是一个动态的非线性问题，传统的梯度优化方法存在着求解方程推导复杂、求解过程不稳定、甚至发散的问题，并且容易在迭代过程中陷入局部最优解，达不到全局寻优的目的。面对传统优化方法中存在的问题，近年来发展了一种新的优化算法——自适应响应面法（Auto Response Surface Method，ARSM），该方法具有全局寻优的特点[2-4]。它是利用初始设计点构建一阶的多项式代理模型，来近似拟合目标函数和约束函数，在后续的寻优迭代过程中，通过不断生成新的设计点来更新近似模型，利用新的模型继续寻找最优点，直到满足函数的收敛准则，即最后两次迭代的目标值变化小于给定值为止[5]。下面将以某新能源电池包模型为例，通过变量筛选、构建多项式代理模型，利用自适应响应面法对该电池包进行基于机械冲击安全性的尺寸优化，来验证该方法的准确性。

1 电池包的CAE 仿真

根据GB/T 31467.3—2015《电动汽车用锂离子动力蓄电池包和系统 第3 部分：安全性能要求和测试方法》要求，对某厂电池包拖脚处施加脉宽15 ms、25 g 的半正弦脉冲。表1 为电池包各关键部位的受力情况，可知电池包整体最大应力为995.3 MPa，最大应力点位于箱体中间横梁位置。此处材料为S700MC，抗拉强度在800～950 MPa，最大应力已略超抗拉极限，所以该位置存在较大的断裂失效风险，在后续尺寸优化中要重点关注。

表1 电池包关键部件受力情况

2 自适应响应面法

2.1 响应面算法

响应面方法（Response Surface Methodology，RSM）是通过多项式函数来拟合设计空间。它可以利用较少的试验在局部范围内比较精确的逼近函数关系，并利用简单的代数表达式展现出来，计算简单，还提升了设计优化的效率。通过回归模型的选择，可以拟合复杂的响应关系，具有良好的鲁棒性。其实际函数f（x）的拟合函数可由式（1）表示：

其中，φ（x）表示基函数，i 表示基函数个数，ε（x）表示基函对应的系数向量。

2.2 自适应响应面法（ARSM）

传统的响应面代理模型的精度，高度依赖于初始样本设计点分布，如果初始构造的代理模型精度较差，将很难得到最优解，或造成局部收敛。自适应响应面法的优点在于：克服了模型依赖于初始样本点的不足，通过将梯度寻优中生成的新设计点引入到模型中，代理模型可以自动调整多项式的阶数，使得代理模型更加拟合原隐式函数，大大提高了代理模型的收敛性能。其计算方法如下。

假设根据s 个样本点得到基函数系数为ε（x），已知矩阵为Xs，则第s+1 个样本点，得到的响应值为f（xs+1），已知矩阵Xs+1和ε（s+1）的表达式如下：

3 电池包的尺寸优化模型

电池包的初始质量Mass=96.3 kg，机械冲击危险区域最大应力为Force=995 MPa，则其优化模型可以通过设置设计变量、目标函数和约束函数来设置，其数学表达式为：

设计变量：t1、t2、t3、t4

目标函数：Min（Mass）

约束函数：Max（Force）＜995 MPa

根据建立的优化模型，利用自适应响应面法进行优化计算（图1）。其中，CAE 即Computer Aided Engineering，计算机辅助工程。

图1 自适应响应面法计算流程

3.1 拉丁超立方试验设计取样

在响应面开始构造之前，需要生成一定数量的初始设计点，用于代理模型的拟合计算，本文采用拉丁超立方设计来进行初始设计点选取。其原理是在n 维空间中，将每一维度的坐标均匀的等分为m 个区间。随机选取m 个点，保证一个因子的每个水平只被研究一次，即构成n 维空间，样本数为m 的拉丁超立方设计，记为LHD。拉丁超立方设计具有有效的空间填充能力，与正交试验相比，拉丁方设计用同样的点数可以研究更多的组合。在本文优化模型中，利用拉丁超立方试验设计4 个初始样本点，加上电池包模型的初设值，共5 个样本点，可以用于构造初始的一阶响应面模型。

3.2 优化结果分析与验证

根据上述由拉丁方设计样本点构造的初始响应面，进行寻优迭代计算，迭代过程明细见表2，质量和最大应力迭代过程如图2、图3 所示。从表2 可以看出，在迭代步1、2、4、6、9～11 中，虽然电池包总体质量有所降低，但是最大应力值均超过了约束条件；而在迭代步7、8、12 中，最大应力值有所下降，但是总体质量增加，起不到减重的效果。综合比较，迭代步13 中，电池包模型的总体质量有所下降，单元最大应力值同样有所降低，是本次优化计算中的最优解。这证明ARSM 自适应响应面算法可以在实现电池包轻量化的同时，提高电池包在机械冲击工况下的安全性能。由表2 中的数据可分析出，电池包中最大应力值的下降，主要是因为电池包受力危险区域的横梁（材料S700MC）增厚所产生的作用。

表2 ARSM 模型的寻优迭代历程

图2 电池包质量迭代过程

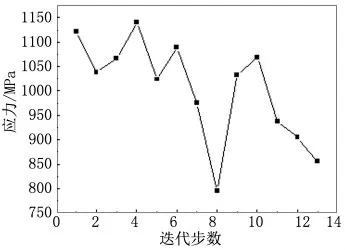
图3 最大应力迭代过程

根据ARSM 算法计算出的最优解13，将横梁、地板、侧围、支架这4 个关键零部件的厚度，依次设置为2.5 mm、1.5 mm、1.7 mm、2.0 mm，经CAE 模型计算得出各部位的受力情况（表3）。其中，横梁和侧围厚度优化后，受力情况得到改善，地板和支架受力有所增加，但是均在所使用材料的抗拉强度范围之内；优化后电池包总重量94.2 kg，相比初始的96.3 kg，质量降低约2.2%。这一结果表明，通过自适应响应面法得到的最优解是满足电池包尺寸优化要求的，可以作为实现汽车零部件尺寸优化工作的有效方法。

4 结论

通过采用自适应响应面法进行电池包模型尺寸优化的结果表明，该方法初期利用拉丁超立方等DOE（Design of Experiment，试验设计）方法生成一阶多项式近似模型所需的高精度初始设计点，然后通过不断的将计算结果，引入到模型中进行响应面近似模型的自动更新、优化，有效减少了迭代次数，并且提高了近似响应面的拟合精度。利用自适应响应面法在实现了电池包模型质量降低的同时，合理分配了各部件的厚度，改善了电池包关键部位的受力情况，提高了电池包在机械冲击工况下的安全性能。

表3 优化前后对比